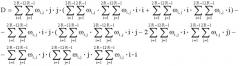Устройство адаптивной фильтрации видеосигналов

Устройство адаптивной фильтрации видеосигналов

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к информационно-измерительным устройствам и может быть использовано в вычислительной технике, в системах управления и обработки изображений и видеосигналов.

При решении задач сглаживания изображений с целью ослабления действующих аддитивных помех рассматривается модель статического изображения, которая представляет собой двумерную дискретную последовательность Y_i,j, i = 1, N ¯ , j = 1, M ¯ вида:

Y i , j = S i , j + η i , j , i = 1, N ¯ ,   j = 1, M ¯ ,                                       ( 1 )

где S_i,j - полезная двумерная составляющая (исходное неискаженное изображение), η_i,j - аддитивная шумовая составляющая, N - количество строк, М - количество столбцов двумерного массива изображения.

Изображение можно рассматривать как прямоугольную матрицу Y={Y_i,j}, со строками i и столбцами j, где N и М - определяют размер матрицы изображения в пикселях.

В случае динамического изображения рассматривается модель, которая представляет собой двумерную дискретную последовательность Y i , j ( k ) , i = 1, N ¯ , j = 1, M ¯ , k = 1, K ¯ , вида:

Y i , j ( k ) = S i , j ( k ) ,       i = 1, N ¯ ,     j = 1, M ¯ ,     k = 1, K ¯ ,                         ( 2 )

где S i , j ( k ) - полезная двумерная составляющая (исходное неискаженное изображение), S i , j ( k ) - аддитивная шумовая составляющая, N - количество строк, М - количество столбцов двумерного массива изображения, К - количество кадров двумерного массива динамического изображения.

Основная решаемая задача - фильтрация динамических цифровых изображений в условиях ограниченного объема априорных данных.

Подобная задача может возникнуть: 1) в работе приемо-передающих устройств дальней или космической связи; 2) в радиотехнике при обработке сигналов; 3) в системах цифровой обработки динамических изображений; 4) в метеорологии и экономике при обработке результатов измерений.

При обработке динамических изображений используется два основных подхода. Первый из них основан на использовании корреляционной связи между кадрами. Предполагается, что кадры в пределах небольшого интервала времени изменяются незначительно, при этом можно применить все методы, описанные выше, где в качестве пространства обработки используется зависимость амплитуда - номер кадра.

Данный подход имеет недостатки, связанные с выбором количества кадров для обработки. Наличие в видеоряде динамических сцен приводит к расфокусировке и искажению полезного сигнала.

Второй подход для фильтрации динамических изображений основан на обработке кадра как отдельного изображения, и, как следствие, рассмотренные методы повторяют все недостатки методов фильтрации статических изображений.

Известен способ скользящего среднего [Гонсалес Р. Цифровая обработка изображений / Р.Гонсалес, Р.Вудс. - М.: Техносфера. - 2005. - 1072 с.]. Для его использования достаточно одной реализации Y_i,j, i = 1, N ¯ , j = 1, M ¯ исходного процесса.

Для исходного изображения определяется размер маски сглаживающего фильтра m, т.е. натуральное число m<N. Способ скользящего среднего предполагает запоминание исходного изображения Y_i,j, i = 1, N ¯ , j = 1, M ¯ , определение размера маски фильтра m (ширины «скользящего окна»), для которого производится вычисление среднего арифметического, S ¯ i , j = 1 m ⋅ m ⋅ ∑ i = 1 m ∑ j = 1 m Y i , j , замену центрального из значений Y_i,j, i = 1, N ¯ , j = 1, M ¯ найденным средним S ¯ i , j , сдвиг «скользящего окна» на одно значение вправо, вычисление среднего арифметического выбранных значений реализации, и так до тех пор, пока маска фильтра не переместится по всему изображению.

Ширину "окна" выбирают нечетной, т.к. сглаженное значение рассчитывается для центрального значения.

Признаки устройства-аналога, совпадающие с признаками заявляемого технического решения, следующие: запоминание дискретного сигнала, выделение временных отрезков, нахождение среднего арифметического значения сигнала, попавших в выделенные отрезки времени, замена исходной двумерной дискретной реализации результатов измерений сглаженными значениями.

Недостатками известного устройства являются:

- неспособность обрабатывать строки или столбцы изображения, находящиеся на границах маски в случае, если центр фильтра приближается к границам изображения;

- способ скользящего среднего вызывает автокорреляцию остатков, даже если она отсутствовала в исходной полезной составляющей (эффект Слуцкого-Юла).

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:

- если ширина "окна" сглаживания равна 2р+1, то первые p и последние p значений исходной реализации результатов измерений не подвергаются обработке;

- поскольку центральное значение "окна" сглаживания вычисляется как среднее арифметическое соседних, то значения оценки полезной составляющей становятся зависимыми.

В качестве нелинейных фильтров используются фильтры, основанные на порядковых статистиках [Гонсалес Р. Цифровая обработка изображений / Р.Гонсалес, Р.Вудс. - М.: Техносфера. - 2005. - 1072 с.]. Отклик такого фильтра определяется предварительным упорядочиванием (ранжированием) значений пикселей, покрываемых маской фильтра, и последующим выбором значения, находящегося на определенной позиции упорядоченной последовательности (т.е. имеющего определенный ранг). Фильтрация сводится к замещению исходного значения (в центре маски) на полученное значение отклика фильтра. Наиболее известен медианный фильтр, который заменяет центральное значение маски фильтра на значение медианы распределения всех значений результатов измерений, принадлежащих области маски фильтра. Чтобы выполнить медианную фильтрацию для элемента изображения, необходимо сначала упорядочить по возрастанию значения пикселей внутри маски, затем найти значение медианы и присвоить полученное значение обрабатываемому элементу.

Признаки устройства-аналога, совпадающие с признаками заявляемого технического решения, следующие: дискретизация сигнала по времени, запоминание входной реализации результатов измерения, выделение временных отрезков, замена входной реализации результатов измерения сглаженными значениями.

Недостатками известного устройства являются:

- неспособность обрабатывать строки или столбцы изображения, находящиеся на границах маски в случае, если центр фильтра приближается к границам изображения;

- вследствие нелинейности метода обработки нельзя строго разграничить влияние медианной фильтрации на сигнал и шум;

- медианное сглаживание можно рассматривать только как эффективный метод предварительной обработки входной реализации результатов измерений в случае импульсных помех.

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:

- медианная фильтрация является нелинейным методом обработки;

- зависимость эффективности сглаживания результатов измерений от формы полезной и шумовой составляющей.

Структурная схема устройства, реализующего рассмотренный способ, содержит генератор тактовых импульсов, коммутатор, блок управления, регистр хранения, блок ранжирования, блок выбора среднего значения, выходной регистр, где хранится оценка исходной дискретной реализации результатов измерений.

Известен способ наименьших квадратов и устройство для кусочно-линейной аппроксимации [Бендат Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. - М.: Мир, 1989. - 540 с., авторское свидетельство №1624479]. Для использования данного способа достаточно одной одномерной реализации Y₁, Y₂, …, Y_N исходного процесса.

Способ наименьших квадратов позволяет для результатов измерений Y_l, Y₂, …, Y_N исходного процесса получить оценку, k = 1, N ¯ , минимизируя целевую функцию вида:

∑ k = 1 N ( Y k − S ¯ k ) 2 → min

В случае, когда S ¯ k представляет собой полином первой степени , коэффициенты а и b можно найти, минимизируя целевую функцию вида:

Дифференцируя выражение (3) по а и b и приравнивания к нулю, получаем систему линейных уравнений:

Решением системы является:

b = k = ∑ k = 1 N k ⋅ Y k − 1 N ∑ k = 1 N k ⋅ ∑ k = 1 N Y k ∑ k = 1 N k 2 − 1 N ( ∑ k = 1 N k 2 )

При оценке сумма квадратов отклонений значений оценки от значений реализации измерений является минимальной.

Признаки устройства-аналога, совпадающие с признаками заявляемого технического решения, следующие: запоминание дискретного сигнала, аппроксимация по методу наименьших квадратов, замена исходной дискретной реализации результатов измерений аппроксимированными значениями.

Недостатками известного способа являются:

- при использовании данного способа необходима априорная информация о функции полезного сигнала;

- ошибка полезной составляющей имеет вдоль реализации, в общем случае, нелинейную зависимость и достигает своих максимальных значений на границах интервала аппроксимации;

- при не полиноминальной модели оценки полезной составляющей строгое решение задачи минимизации целевой функции способа наименьших квадратов не всегда существует в силу нелинейности решаемой системы уравнений;

- ограниченность способа наименьших квадратов к распараллеливанию и построению системы многоканальной обработки.

Причины, препятствующие достижению требуемого технического результата, заключается в следующем:

- эффективность оценки полезной составляющей зависит от объема реализации, статистических характеристик аддитивного шума и наличия априорной информации о функциональной зависимости модели полезной составляющей.

Структурная схема устройства для кусочно-линейной аппроксимации содержит группу последовательно соединенных регистров, первый и второй вычитатели, сумматор, первый и второй накапливающие сумматоры, элементы задержки, генератор тактовых импульсов, два умножителя и два делителя на постоянный коэффициент.

Известен способ и устройство фильтрования шума видеосигналов (патент №2364937, МПК G06K 9/40). Изобретение относится к области обработки видеоинформации, и в частности, к способам пространственно-временного устранения шумов в видеоизображениях. Техническим результатом является повышение скорости фильтрования шумов видеоизображения с обеспечением высокого качества шумоподавления без внесения искажений. Способ фильтрования шума видеосигналов устойчив к движению и основан на определении локальной структуры и на нелокальном усреднении в соответствии с определенной структурой кадра и с использованием данных о текущем кадре и соседних кадрах, при котором определяют локальную структуру изображения путем последовательного свертывания предопределенных шаблонов с соседними пикселями и путем отбора образцового шаблона RP_c, который выдает наименьшую ошибку после свертывания, выполняют пространственно-временную фильтрацию с помощью взвешенного усреднения значений пикселя в поисковом окне от опорного кадра, причем результат пространственно-временной фильтрации вычисляют следующим образом:

Re s P x l = 1 N o r m 2 ⋅ ∑ − T / 2 T / 2 ∑ − K / 2 K / 2 ∑ − L / 2 L / 2 w f ⋅ p i x r ( x r + p , y r + s , t r )

где pix_r(x_r, y_r, t_r) обозначает опорный пиксель от опорного кадра t_r=t_c+t с координатами х_r и y_r, индекс p изменяется от − L 2 до L 2 в направлении X, индекс s изменяется от − K 2 до K 2 в направлении Y, индекс t изменяется от − T 2 до T 2 в области времени, Т - число опорных кадров, вовлеченных в процесс фильтрования, w_f - вес опорного пикселя pix_r(x_r, y_r, t_r), нормирующий множитель вычисляют как:

N o r m 2 = ∑ − T / 2 T / 2 ∑ − K / 2 K / 2 ∑ − L / 2 L / 2 w f

вес w_f каждого опорного пикселя определяют следующим образом

w f = { w ( x r , y r , σ r , σ f )       е с л и   R P c = R P r 0     в     п р о т и в н о м     с л у ч а е ,

если образцовый шаблон RP_с текущего пикселя совпадает с образцовым шаблоном опорного пикселя RP_r, то опорный пиксель считают корректным, в противном случае, когда образцовые шаблоны текущего пикселя и опорного пикселя разные, считают, что опорный пиксель является некорректным, и исключают его из процесса удаления шумов.

Признаки устройства-аналога, совпадающие с признаками заявляемого технического решения, следующие: считывание кадров видеопоследовательности, фильтрация видеоизображения с обеспечением высокого качества шумоподавления без внесения искажений.

Недостатками известного способа являются:

- при использовании данного способа необходима априорная информация о функции полезного сигнала;

- при не полиноминальной модели оценки полезной составляющей строгое решение задачи минимизации целевой функции способа наименьших квадратов не всегда существует в силу нелинейности решаемой системы уравнений;

- ограниченность способа наименьших квадратов к распараллеливанию и построению системы многоканальной обработки;

- ресурсоемкие вычислительные затраты.

Причины, препятствующие достижению требуемого технического результата, заключается в следующем:

- эффективность зависит от объема реализации, статистических характеристик шума и наличия априорной информации о функциональной зависимости модели полезной составляющей.

Структурная схема устройства для фильтрования шума видеосигналов содержит блок памяти, блок оценки уровня, блок размывки, блок вычисления веса фильтра, блок применения фильтра, блок определения локальной структуры, регистры.

Наиболее близким к изобретению является адаптивный двумерный способ размножения оценок и устройство, его реализующее (патент №2461874, МПК G06F 17/17). Рассматриваемое устройство-прототип предполагает формирование адаптивных областей двумерного сигнала для каждого значения пикселя, в связи чем задаются восемь направлений h = 1 ,8 ¯ , в которых определяются интервалы квазистационарности (фиг.1). Условие квазистационарности проверяется с помощью вычисления случайной величины τ, равной сумме числа инверсий значений пикселей в каждом из восьми направлений двумерного сигнала Y_i,j, i = 1, N ¯ , j = 1, M ¯ .

Данные границы позволяют получить интервалы с монотонным изменением яркости сигнала. Далее все восемь полученных секторов объединяются в одну область Ω. Таким образом, для каждого пикселя формируется окрестность пикселей, близких по значению яркости.

Значения пикселей, попавшие между всеми направлениями и интерполирующими прямыми, проходящими через границы интервалов квазистационарности, объединяются в одну область Ω и аппроксимируются поверхностью первого порядка вида.

Процедура получения области Ω и вычисление оценки S ˜ i , j повторяется для каждого значения пикселя Y_i,j, i = 1, N ¯ , j = 1, M ¯ , при этом формируется весовая функция W_i,j, i = 1, N ¯ , j = 1, M ¯ , значения которой равны количеству размноженных оценок для каждого пикселя.

Результирующая оценка изображения S ¯ i , j определяется как среднее арифметическое размноженных адаптивных оценок:

S ¯ i , j = ∑ t = 1 K S ˜ i , j t W i , j ,   i = 1, N ¯ ,     j = 1, M ¯

Недостатками известного устройства-прототипа являются:

- невозможность реализации известного способа в реальном масштабе времени;

- большие вычислительные затраты.

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:

- для использования способа размножения необходимо запоминать всю входную реализацию, то есть кадр видеопоследоватльности.

Устройство, реализующее адаптивный двумерный способ размножения оценок, содержит (фиг.2): блок хранения входной реализации, блок поэлементного умножителя, блок определения участков квазистационарности, блок формирования маски, блок аппроксимации, блок хранения оценок, блок усреднения оценок, блок хранения оценки полезной составляющей, счетчик текущей строки, блок задержки, генератор сигнала усреднения, счетчик текущего столбца, генератор тактовых импульсов.

Суть предлагаемого устройства адаптивной фильтрации видеосигналов заключается в следующем. Упрощенная математическая модель входного двумерного сигнала представляется в соответствии с выражением (1).

На основе адаптивного двумерного способа размножения оценок и устройства, его реализующего, предлагается устройство адаптивной фильтрации. На первом этапе происходит выделение кадра из видеопоследовательности. Далее для формирования адаптивных областей двумерного сигнала для каждого значения пикселя задаются восемь направлений h = 1 ,8 ¯ (фиг.1), в которых определяются интервалы квазистационарности. Условие квазистационарности проверяется с помощью вычисления случайной величины τ, равной сумме числа инверсий значений пикселей в каждом из восьми направлений (фиг.1) двумерного сигнала Y_i,j, i = 1, N ¯ , j = 1, M ¯ .

Например, сумма числа инверсий для направления 5 равна:

τ d = ∑ l = 0 d − 1 ∑ k = l + 1 d u ( Y i + l , j , Y i + k , j ) ,         d = 1, R ¯

u ( Y i + l , j , Y i + k , j ) = { 1, Y i + l , j > Y i + k , j , 0, Y i + l , j ≤ Y i + k , j .

где i=const, j=const; Y_i,j - текущее значение пикселя изображения с координатами (i, j); Y_i+l,j, l=i+1…d - последующие значения пикселей изображения по j-му столбцу (движение в направлении 5), d≤R, R - максимальная длина интервала квазистационарности.

Количество сочетаний, для которых вычисляется сумма инверсий, составляет:

X = d ⋅ ( d − 1 ) 2 .

Первая альтернатива (убывающий сигнал) принимается, если:

τ d > c 1 = τ α 2 ⋅ X + X / 2 − 0,5

Правило для принятия второй альтернативы (возрастающий сигнал) имеет вид:

τ d > c 2 = τ 1 − α 2 ⋅ X + X / 2 − 0,5

Гипотеза о стационарности сигнала принимается, если с₂≤τ_d≤с₁, где α - априорно задаваемое значение ошибки первого рода.

По полученным границам интервалов для каждого из восьми секторов, образованных направлениями 1-2, 2-3, 3-4, 5-6, 7-8, 8-1, формируются области квазистационарности. Для этого используется линейная интерполяция границ смежных интервалов уравнением прямой, проходящей через две точки:

j − j 1 j 2 − j 1 = i − i 1 i 2 − i 1 , i = i 2 − i 1 j 2 − j 1 ⋅ j + i 1 ⋅ j 2 − i 2 ⋅ j 1 j 2 − j 1 ,

где (i₁, j₁) - координаты границы направления h, (i₂, j₂) - координаты границы направления h+1.

Для направлений h = 1 ,8 ¯ на изображении для одномерных реализаций, полученных из значений пикселей по вертикальным и диагональным направлениям от центрального пикселя исходного изображения, определяются интервалы квазистационарности с помощью способа инверсий. Данные границы позволяют получить интервалы с монотонным изменением яркости сигнала. Далее все восемь полученных секторов объединяются в одну область Ω. Таким образом, для каждого пикселя формируется окрестность пикселей, близких по значению яркости.

Значения пикселей, попавшие между всеми направлениями и интерполирующими прямыми, проходящими через границы интервалов квазистационарности, объединяются в одну область Ω и аппроксимируются поверхностью первого порядка вида , где ω_i,j, i = 1,2 ⋅ R − 1 ¯ , j = 1,2 ⋅ R − 1 ¯ значения бинарной маски, которая принимает значения, равные:

ω i , j = { 1, i , j ∈ Ω 0, i , j ∉ Ω , i = 1,2 ⋅ R − 1 ¯ ,   j = 1 ,2 ⋅ R − 1 ¯

Значения коэффициентов А, В и С определяются с помощью двумерного способа наименьших квадратов [Патент №2362207 Российская Федерация, С2, МПК G06F 17/17. 2007127727/09; Заяв. 19.07.2007; Опубл. 20.07.2009, Бюл. №20], для нахождения которых минимизируется целевая функция вида:

∑ i = 1 2 ⋅ R − 1 ∑ j = 1 2 ⋅ R − 1 ( ( Y i , j − S ˜ i , j ) ⋅ ω i , j ) 2 → min

∑ i = 1 2 ⋅ R − 1 ∑ j = 1 2 ⋅ R − 1 ( ( Y i , j − A ⋅ i − B ⋅ j − C ) ⋅ ω i , j ) 2 → min                           ( 2 )

Дифференцируя выражение (2) по А, В и С и приравнивания к нулю, получаем систему линейных уравнений:

{ ∂ ( ∑ i = 1 2 ⋅ R − 1 ∑ j = 1 2 ⋅ R − 1 ( Y i , j − A ⋅ i − B ⋅ j − C ) ⋅ ω i , j ) 2 / ∂ A = 0, ∂ ( ∑ i = 1 2 ⋅ R − 1 ∑ j = 1 2 ⋅ R − 1 ( Y i , j − A ⋅ i − B ⋅ j − C ) ⋅ ω i , j ) 2 / ∂ B = 0, ∂ ( ∑ i = 1 2 ⋅ R − 1 ∑ j = 1 2 ⋅ R − 1 ( Y i , j − A ⋅ i − B ⋅ j − C ) ⋅ ω i , j ) 2 / ∂ C = 0 ;                                   ( 3 )

Решением системы (3) является:

A =