Способ доплеровской фильтрации ионосферных сигналов

Способ доплеровской фильтрации ионосферных сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области дискретного спектрального анализа, к области систем обработки информации и измерительной техники, и может быть использовано для доплеровской фильтрации (выделения) лучевой структуры ионосферных сигналов.

При ионосферном распространении радиоволн декаметрового диапазона в точку приема часто приходят несколько лучей (от 1 до 4-х и более), отраженных от разных областей ионосферы. Вследствие динамических процессов в ионосфере частоты отдельных лучей имеют доплеровские сдвиги ω_m (в пределах от нуля до долей Герца). В результате на поверхности земли создается сложное интерференционное распределение напряженности поля. В этих условиях для доплеровской фильтрации лучевой структуры ионосферных сигналов с помощью спектрального анализа требуются временные интервалы обработки от 40 секунд до 100 и более /1/. Однако на таких временных интервалах амплитуда, фаза и частота отдельных лучей ионосферного сигнала меняются за счет изменения ионосферных параметров. В связи с этим доплеровский спектр ионосферного сигнала становится неустойчивым (случайным). Разрешающей способности спектрального анализа часто оказывается недостаточно для выделения лучевой структуры ионосферных сигналов. В результате возникают интерференционные ошибки в комплексах аппаратуры, работающих на основе ионосферных сигналов, таких как пеленгация, локация, навигация, системы связи. Для решения задачи доплеровской фильтрации требуется уменьшение временного интервала обработки до ~20 с и менее.

Известны способы оценки параметров совокупности синусоидальных сигналов с помощью спектрального анализа в системах обработки информации и в измерительной технике. В этом случае используют узкополосный фильтр, частота которого перестраивается в определенной частотной области. Максимумы амплитудно-частотной характеристики определяют несущие частоты сигнала f_m, значение максимумов определяют амплитуды u_0,m, а значение фазочастотной характеристики в точках f=f_m определяют начальные фазы сигнала φ_0,m (патент RU №2137143 от 10.09.1999 г; патент RU №2229725 от 27.05.2004 г.; патент RU №2399919 от 20.09.2010; патент РФ 2276375 от 10.05.2006, патент Рф 2133041 от 10.07.1999 г.). Недостатком этих способов спектрального анализа является то, что они выделяют спектральные линии лишь при выполнении критерия Рэлея, т.е. когда различия между частотами спектральных линий больше чем 1/T (Δf=|f_m-f_n|≥1/T). Для ионосферных сигналов данное условие часто не выполняется, и указанные способы спектрального анализа могут определять ложные спектральные линии.

Известны способы измерения параметров синусоидального сигнала по аналитическим выражениям, получаемым по нескольким временным отсчетам сигнала (заявка РФ 93057353/09 от 24.12.1993 г., заявка РФ 94038816 от 27.05.1997 г.). Данные способы позволяют определять параметры одной или нескольких спектральных составляющих сигнала на малых интервалах времени в области, где критерий Рэлея не выполняется. К недостаткам этих способов оценки параметров можно отнести то, что вследствие ограниченного количества временных отсчетов (количество отсчетов определяется количеством неизвестных параметров сигнала) помехоустойчивость оказывается невысокой. Отсутствует статистическое усреднение. Использование дополнительных отсчетов сигнала при наличии шумовой добавки приводит к системе несовместных алгебраических уравнений.

Известные методы сверхразрешения типа Прони, предсказаний, «Music», Писаренко, и ряд других методов, хорошо представленных в /2/, позволяют получать оценки частотных составляющих сигнала в области, где не выполняется критерий Рэлея. Они могли бы быть основой для доплеровской фильтрации ионосферных сигналов. Однако эти методы не имеют достаточного теоретического обоснования. В частности, при малых значениях дискретизации Δt, когда Δf=|f_ш-f_n|□f_m детерминант корреляционной матрицы близок к нулю. В результате решения оказываются неустойчивыми. Появляются ложные частотные составляющие. Кроме того, существует проблема оценки количества спектральных составляющих сигнала M.

Известен способ гармонического анализа периодического многочастотного сигнала (патент РФ №2435168 от 27.11.2011 г.). Он заключается в том, что за счет подбора весовых функции при обработке сигнала устанавливаются нули на частотах сопутствующих спектральных линий, кроме одной выделяемой спектральной линии. При наличии ложных спектральных линий ионосферного сигнала при интерференции данный метод не может использоваться. Не решается проблема оценки количества составляющих сигнала M. Достоверность решения задачи выделения спектральных линий ионосферного сигнала оказывается низкой.

Наиболее близким к предлагаемому изобретению (прототип) является «Способ оценки параметров широкополосных сигналов по методу Прони» (патент РФ №2430382 от 16.12.2008 г.). Данный способ позволяет получать оценки частотных составляющих сигнала в области, где не выполняется критерий Рэлея (на малых интервалах времени). Для оценок параметров спектральных составляющих в этом способе используется или матрица данных, или корреляционная матрица /2/. Оценки, полученные методом Прони, далее многократно уточняются с помощью аддитивных поправок до получения стабильного результата.

Обоснованием данного способа является следующее. Рассмотрим дискретный комплексный сигнал , содержащий M спектральных составляющих.

где - комплексная амплитуда m-составляющей сигнала.

ω_m- круговая частота m-составляющей сигнала.

Исключая отдельные частотные составляющие, можно получить матричное соотношение с неопределенными коэффициентами .

Матрица данных в (2) имеет размерность M и составляется совместно с правым столбцом по 2М отсчетам данных . Решение матричного уравнения (2) позволяет определить неопределенные коэффициенты . На основании этих коэффициентов составляется полином

Факторизация полинома позволяет определить его корни , а следовательно, и частоты спектральных составляющих сигнала ω_m. При оцененных частотах ω_m, подставляя их в выражение (1), можно решить систему N=М (n=1÷N) линейных уравнений относительно амплитуд .

Данное решение является статистически неустойчивым и может оценивать параметры спектральных составляющих лишь при высоких отношениях сигнал/шум. Для увеличения статистической устойчивости решения используют избыточное количество отсчетов данных, N>2M, по которым производят усреднение методом наименьших квадратов /2/. В результате получают корреляционную матрицу с элементами и правым столбцом

,

Где черта сверху означает суммирование по индексу n.

Звездочка «*» означает комплексное сопряжение.

Полученное матричное уравнение (5) эквивалентно уравнению (2). Однако вследствие усреднения по индексу n его решение (неопределенные коэффициенты ) статистически более устойчиво.

После нахождения амплитуд и частот ω_m спектральных составляющих используется их уточнение с помощью малых поправок , Δω_m.

Недостатком этого способа является следующее. При малых различиях частот спектральных составляющих по сравнению с частотой спектральной линии Δf=|f_m-f_n|□f_m интервал дискретизации Δt, согласно теореме Котельникова, должен быть мал . В результате детерминант матрицы данных (2) (матрицы Прони), а также детерминант корреляционной матрицы (4) будут близки нулевому значению. Это приводит к неустойчивости решений при малых отношениях сигнал/шум и появлению спектральных линий на ложных частотах. Использование аддитивных поправок в данных условиях уточняет как истинные спектральные линии, так и ложные. По существу отсутствует критерий отбора решений при использовании аддитивных поправок. Кроме того, существует проблема оценки количества составляющих сигнала M. Достоверность получаемых этим способом оценок параметров спектральных составляющих оказывается низкой. Данный способ оценки параметров сигнала, содержащий ряд частотных составляющих, принятый нами за прототип, осуществляют следующим образом.

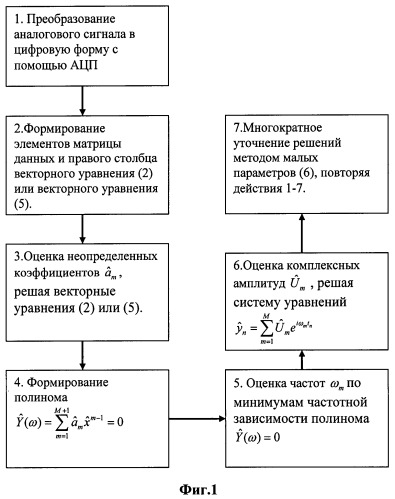
1. Принятый сигнал, содержащий N-спектральных составляющих, преобразуют в дискретную цифровую последовательность с интервалом дискретизации Δt в соответствии с теоремой Котельникова.

2. Формируют элементы матрицы данных и правого столбца (2) или элементы корреляционной матрицы и элементы правого столбца (4).

3. Решая матричное уравнение (3) или (5) получают значения неопределенных коэффициентов .

4. Формируют полином степени M, используя значения коэффициентов , и получают частотную зависимость полинома .

5. По минимумам модуля полинома оценивают частоты ω_m оставляющих сигнала.

6. Оценивают комплексные амплитуды составляющих сигнала, подставляя оценочные частоты ω_m в уравнения (1) со значениями индекса n=1÷M и решая его относительно амплитуд.

7. Многократно уточняют решения, подставляя выражения (6) в выражение (1) и оставляя лишь слагаемые с малыми добавками , Δω_m в первой степени.

Целью предлагаемого изобретения (технический результат) является:

- повышение точности и достоверности оценок доплеровского спектра многолучевых ионосферных сигналов,

- расширение возможностей спектрального анализа в область малых интервалов обработки сигналов, где критерий Рэлея не выполняется.

Технический результат достигается тем, что ионосферный сигнал, состоящий из M-лучей, каждый из которых имеет доплеровский сдвиг частоты ω_m и комплексную амплитуду , принимают с помощью антенны, усиливают, фильтруют и преобразуют по частоте в приемнике. Аналоговый сигнал на выходе приемника на промежуточной частоте оцифровывают с помощью аналого-цифрового преобразователя (АЦП), формируя избыточную выборку данных, размером N (N≥3M). Снижают с помощью преобразования Фурье промежуточную частоту сигнала до нулевого значения. Преобразуют сигнал к выражению с неопределенными коэффициентами согласно выражению (7).

Определяют коэффициенты корреляционной матрицы (, черта сверху означает суммирование по индексу n) и правого вектора - столбца (, p=1÷M) векторного уравнения

Находят неопределенные коэффициенты c ^ m , решая векторное

уравнение (8), определяют частотную зависимость функционала правдоподобия Δ(ω) /6/ согласно (9)

По максимумам частотной зависимости функционала Δ(ω) оценивают частоты спектральных линий ионосферного сигнала ω_m. По значениям функционала в максимумах Δ(ω_m) определяют достоверность каждого m-решения. Чем больше функционал, тем достовернее и точнее m-решение.

Определяют элементы матрицы (, черта сверху означает суммирование по индексу n) и правого вектора - столбца .

Находят комплексные амплитуды U ^ m спектральных линий ионосферного сигнала решая векторное уравнение (10)

,

Существенные отличия предлагаемого способа доплеровской фильтрации от прототипа следующие.

- Снижают несущую частоту сигнала до нулевой. В этом случае значение интервала дискретизации Δt наиболее оптимальное и детерминант корреляционной матрицы максимально отличается от нуля. Решение матричного уравнения оказывается максимально устойчивым.

- Выражение с неопределенными коэффициентами (7) отличается от аналогичного выражения (2) в прототипе своей правой частью. Это исключает действия, связанные с формированием полинома (3) в прототипе и его факторизацию.

- В отличие от прототипа вводится функционал правдоподобия /6/ (9). Его частотная зависимость дает возможность оценки частот составляющих сигнала, а значения функционала в максимумах Δ(ω_m) является критерием отбора m-решений. Исключается проблема оценки количества составляющих в сигнале.

Обоснованием предлагаемого способа доплеровской фильтрации ионосферных сигналов является следующее.

Запишем сигнал, содержащий M-частотных составляющих, имеющих доплеровские частоты ω_m в виде

Y ^ 1 n = ∑ m = 1 M U ^ m e i ( ω 0 + ω m ) t n                                                             ( 11 )

где U ^ m - комплексная амплитуда m-составляющей ионосферного сигнала,

t_n - время отсчетов при дискретизации (n - меняется в пределах от 1 до 2М и более,

ω_m - доплеровский сдвиг частоты m - составляющей ионосферного сигнала.

ω₀ - промежуточная частота приемника.

Используя формулы преобразования Фурье, исключаем промежуточную частоту приемника ω₀. В результате получим последовательность данных Y ^ n , аналогичную последовательности данных (1) в прототипе y ^ n

Y ^ n = ∑ m = 1 M U ^ m e i ω m t n                                                                                                                 ( 12 )

Используя временную последовательность данных, исключим переменные, описывающие частотные составляющие сигнала ( U ^ m e i ω m t n ) кроме одной.

В результате получим выражение (7) с неопределенными коэффициентами c ^ 1 ÷ c ^ M , выражение в правой части описывает лишь одну составляющую сигнала. Оно отличается правой частью от аналогичного уравнения (2) прототипа.

∑ m = 1 M c ^ m Y ^ n , m = e i ω t n                                                                                                                 ( 7 )

Неопределенные коэффициенты c ^ 1 ÷ c ^ M не зависят от номера вибратора n. Они зависят лишь от временного интервала Δt и можно проводить усреднение по избыточному количеству точек, увеличивая статистическую устойчивость решения. Используя выражение (7) составим функционал правдоподобия Δ1(ω) /6/.

Δ 1 ( ω ) = ∑ n = 1 N | ∑ m = 1 M c ^ m Y ^ n + m − 1 − e i ω t n | 2             ( 13 )

Дифференцируя выражение (13) по неопределенным коэффициентам c ^ m и приравнивая дифференциалы нулю, получим систему уравнений правдоподобия /6/. Выражение (14) определяет p-уравнение правдоподобия.

∑ m = 1 M c ^ m Y ^ n + m − 1 Y ^ n + p − 1 ∗ ¯ = e i ω t n Y n + p − 1 ∗ ¯ ,   p = 1 ÷ M                                                                                                 ( 14 )

Черта сверху означает суммирование по индексу n.

Знак «∗» обозначает комплексное сопряжение.

Из уравнений правдоподобия следует, что элементы корреляционной матрицы A ^ векторного уравнения (8) определены выражением A m , p = Y ^ n + m − 1 Y ^ n + p − 1 ∗ ¯ , а элементы правого столбца b ¯ выражением b ^ p = Y ^ n + p − 1 e − i ω t n ¯ , (p=1÷M). Решая векторное уравнение (8), можно определить неопределенные коэффициенты c ^ m . Подставляя их в выражение для функционала (13) и возводя функционал в квадрат, получим точку на частоте ω. Перебирая все частоты из области определения можно получить частотную зависимость функционала правдоподобия в виде

Δ 1 ( ω ) = 1 − ∑ m = 1 M c ^ m Y ^ n + m − 1 ∗ e i ω t n ¯                                                                                                                         ( 15 ) ,

из которого следует, более удобный, обратный функционал Δ(ω) (9). По максимумам функционала (9) определяются частоты составляющих сигнала ω_m. Значения максимумов функционала правдоподобия (9) определяют достоверность оценок частот. Чем больше значение функционала в максимуме, тем достовернее оценка частоты. Шумовые максимумы определяются уровнем функционала Δ(ω)≤10. Следовательно, значение функционала в максимуме является критерием отбора решений для частот - составляющих сигнала. Найденные частоты спектральных составляющих и их количество позволяют оценить комплексные амплитуды составляющих сигнала, подставляя их в выражение (12) и формируя функционал Δ2.

Δ 2 = ∑ n = 1 N | Y ^ n − U ^ m e i ω m t n | 2                                                                                                             ( 16 )

Дифференцируя (16) по комплексным амплитудам U_m составляющих сигнала можно получить вторую систему уравнений правдоподобия. Выражение (17) представляет p-уравнение правдоподобия.

Y ^ n e − i ω p t n ¯ = U ^ m e i ω m t n e − i ω p t n ¯                                                                                                         ( 17 )

Из уравнений правдоподобия (17) следует структура матрицы A ^ 1 , ее элементы A ^ 1 m , p = e i ( ω m − ω p ) t n ¯ , элементы правого столбца b ^ 1 m = Y ^ n e − i ω m t n ¯ , векторного уравнения (10).

A ^ 1 U ¯ = b ¯ 1 , U ¯ = ( U ^ 1 ÷ U ^ Μ ) T                                                             ( 10 )

Решая это векторное уравнение можно получить комплексные амплитуды U ^ 1 ÷ U ^ M .

Сущность предлагаемого способа пеленгации поясняется следующими рисунками и диаграммами.

На фиг.1 представлена структурная схема устройства, с помощью которого реализуется прототип «Способ оценки параметров широкополосных сигналов по методу Прони».

На Фиг.2 представлена структурная схема устройства, с помощью которого реализуется предлагаемый способ «Способ доплеровской фильтрации ионосферных сигналов».

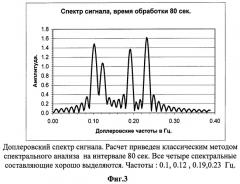
На фиг.3 показан спектр ионосферного сигнала, содержащий четыре частотных составляющих, полученный с помощью модельных расчетов на интервале 80 с с помощью спектрального анализа /4 и 5/. Параметры доплеровских линий спектра следующие: амплитуды U1=1.5, U2=1.1, U3=1.4, U4=1.6; частоты f1=0.1 Гц, f2=0.12 Гц, f3=0.19 Гц, f4=0.23 Гц. Для разрешения (выделения) отдельных составляющих классическим способом спектрального анализа требуется интервал обработки данных 80 с.

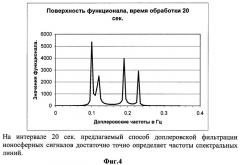
На фиг.4 показана частотная зависимость функционала правдоподобия (9), полученная с помощью модельных расчетов на интервале обработки 20 с (предлагаемый способ). Частоты всех четырех составляющих сигнала определяются по максимумам частотной зависимости. Значения функционала в максимумах изменяются от 2500 и более. Это указывает на большую достоверность и точность получаемых оценок частот составляющих ионосферного сигнала. Интервал обработки 20 с является типичным интервалом, на котором можно ожидать, что параметры ионосферного сигнала будут стационарны.

На фиг.5 показан спектр ионосферного сигнала, полученный на интервале 20 с с помощью классического спектрального анализа /4 и 5/. Первая и вторая составляющие сигнала сливаются в одну линию спектра, аналогично третья и четвертая линии спектра сливаются в одну линию. Интервал 20 с недостаточен для выделения указанных линий спектра. При указанных условиях прототип определяет более четырех частот составляющих спектра ионосферного сигнала по минимумам полинома (3). Оценить достоверность составляющих сигнала не представляется возможным.

На фиг.6 показана статистика амплитуд и частот, полученная с помощью модельных расчетов предлагаемым способом на интервалах 20 с крестиками отмечены модельные данные. Статистика получена по 20 независимым реализациям. Как видно из данного рисунка результаты расчетов достаточно устойчивые. Ложных решений, как в прототипе, нет.

Предлагаемый способ доплеровской фильтрации ионосферных сигналов может быть реализован в устройстве, структурная схема которого представлена на фиг.2 и содержит следующие блоки (последовательность действий).

Блок 1. Принимают аналоговый сигнал приемником, усиливают и преобразуют по частоте до промежуточной частоты выходного блока приемника.

Блок 2. Преобразуют аналоговый сигнал на выходе приемника в цифровую форму с помощью аналого-цифрового преобразователя (АЦП).

Блок 3. Снижают промежуточную частоту цифрового сигнала до нулевого значения с помощью дискретного преобразования Фурье.

Блок 4. Формируют элементы корреляционной матрицы A m , p = Y ^ n + m − 1 Y ^ n + p − 1 * ¯ и правого столбца b ^ p = Y ^ n + p − 1 e − i ω t n ¯ векторного уравнения (8).

Блок 5. Решают векторное уравнения (8) для оценки неопределенных коэффициентов c ^ m .

Блок 6. Формируют частотную зависимость функционала правдоподобия (9), повторяя действия блоков 5 и 6 и меняя частоту в установленных пределах.

Блок 7. Оценивают частоты ω_m составляющих сигнала по максимумам частотной зависимости функционала правдоподобия (9) и их достоверность по значениям максимумов частотной зависимости.

Блок 8. Формируют элементы матрицы A ^ 1 m , p = e i ( ω m − ω p ) t n ¯ и правого столбца b ^ 1 m = Y ^ n e − i ω m t n ¯ векторного уравнения (10).

Блок 9. Решают векторное уравнение (10) для оценки комплексных амплитуд U ^ m .

Литература

1. Афраймович Э.Л. Интерференционные методы радиозондирования ионосферы. М.: Наука, 1982.

2. Марпл-мл. СЛ. Цифровой спектральный анализ и его приложения: Пер. с англ. М.: Мир, 1990. 584 с.

3. «Способ оценки параметров широкополосных сигналов по методу Прони» (патент РФ №2430382 от 16.12.2008 г.).

4. Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов по специальности «Радиотехника». - 2-е изд. - М.: Высшая шк., 1988. - 448 с., 6 ил.

5. Сергиенко А.Б. Цифровая обработка сигналов: Учебное пособие для вузов по специальности «Информатика и вычислительная техника». - СПб.: Питер, 2005. - 604 с. : ил.

6. А.И.Перов. Статистическая теория радиотехнических систем. - М.: Радиотехника, 2003, 400 с., ил.

Способ доплеровской фильтрации ионосферных сигналов, включающий прием ионосферного сигнала с помощью приемника, его усиление и преобразование по частоте, преобразование аналогового сигнала на выходе приемника в цифровую форму с помощью аналого-цифрового преобразователя, отличающийся тем, что снижают промежуточную частоту сигнала до нулевого значения с помощью преобразования Фурье, формируют элементы корреляционной матрицы (черта сверху означает суммирование по индексу n) и правого столбца векторного уравнения , определяют элементы вектора неопределенных коэффициентов , решая в вычислительном устройстве векторное уравнение , формируют частотную зависимость функционала правдоподобия перебирая ч