Способ пеленгации ионосферных сигналов в условиях интерференции лучей

Способ пеленгации ионосферных сигналов в условиях интерференции лучей

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике, а именно, к области пеленгации, и может быть использовано для пеленгации (измерение азимутов) и измерения углов места ионосферных сигналов в условиях приема нескольких интерферирующих лучей в широком частотном диапазоне. При приеме ионосферных сигналов в точку приема, как правило, приходят несколько лучей (1÷4 и более), отраженных от разных слоев ионосферы, с азимутами, находящимися в области главного лепестка диаграммы направленности (~ 5÷10 градусов). Вследствие интерференции суммарный главный лепесток диаграммы направленности антенной системы существенно меняется, создавая ложные пеленги, отличающиеся от истинных пеленгов на десятки градусов.

Известны фазовые способы пеленгации, осуществляемые путем измерений разности фаз между вибраторами антенной системы и оценки по этим измерениям азимутов и углов места (Патент RU №2365931, опубликован 27.08.2009 г.; Патент RU №2429500, опубликован 20.09.2011; Патент RU №2450283, опубликован 10.05.2012 г.; Заявка на изобретение RU №2010143935, опубликована 10.05.2012 г.; Заявка RU №2003108306 от 25.03.2003 г., G01S 3/14, опубликована 10.10.2004 г.). Недостатком вышеуказанных способов является то, что используется только фазовая информации. Это требует для однозначности измерения фаз на вибраторах малого, по сравнению с длиной волны, пространственного разнесения вибраторов

R n + 1 − R n < λ 2 ,

В условиях приема двух (или нескольких) близких по азимуту лучей фазовые способы пеленгации являются неустойчивыми. При разности фаз между лучами ~180° они дают отклонения пеленга на десятки градусов (ложные пеленги).

Известны способы пеленгации по максимуму диаграммы направленности антенной системы (Патент RU №2144200, опубликован 10.01. 2000 г.; Патент RU №2258241, опубликован 10.08.2005 г.; Патент RU №2419805, опубликован 27.05.2011 г.; Патент RU №2201599, опубликован 27.03.2003 г.; Патент RU №2004100714, опубликован 20.06.2005 г.). В этом случае используется временное преобразование Фурье для частотного выделения сигнала от отдельных вибраторов антенной системы и различные формы пространственной обработки данных. Наилучшим образом диаграмма направленности формируется при использовании пространственного преобразования Фурье. В результате создается двумерный комплексный угловой спектр (диаграмма направленности антенной системы). При использовании пространственного преобразования Фурье диаграмма направленности формируется по выражению (комплексный вид):

U ^ ( α ′ , β ′ ) = 1 N ∑ n = 1 N E ^ n e − i K ¯ ( α ′ , β ′ ) R ¯ n ,   ( 1 )

где Ê= E_0,nexp(iψ_n) - комплексная амплитуда напряженности поля ионосферного сигнала в n-точке пространства с радиус-вектором R ¯ n ,

E_0,n,ψ_n - амплитуда и фаза напряженности поля сигнала на n-вибраторе.

K ¯ ( α ′ , β ′ ) - оценочный волновой вектор ионосферного сигнала,

α', β' - оценочные значения азимута и угла места ионосферного сигнала.

Квадрат модуля нормированной диаграммы направленности (расчетная форма) определяется выражением

U 2 ( α ′ , β ′ ) = E n cos ( ψ n − K ¯ ( α ′ , β ′ ) R ¯ n ) ¯ 2 + E n sin ( ψ n − K ¯ ( α ′ , β ′ ) R ¯ n ) ¯ 2 E ¯ n 2 ,   ( 2 )

где черта сверху означает суммирование по индексу «n».

Недостатком вышеуказанных способов, связанных с пространственным преобразованием Фурье, является неустойчивость решения при наличии много лучевой интерференции при разности фаз между лучами ~180°. При приеме двух интерферирующих лучей ионосферного сигнала (различие в азимутах меньше ширины диаграммы направленности) суммарная диаграмма направленности за счет изменения разности фаз между лучами (в области ~180 градусов) в значительной степени подавляется. Боковые или задние лепестки суммарной диаграммы направленности в этих условиях становятся больше, чем основной лепесток диаграммы направленности. В результате азимут (пеленг) в амплитудном способе пеленгации определяется по максимальному боковому или заднему лепестку диаграммы направленности антенной системы. Отклонения азимута (ложные пеленги) достигают десятков градусов.

Известны способы пеленгации, антенная система в которых состоит из ограниченного количества вибраторов (3÷5 вибраторов) (Патент RU №2262119, опубликован 10.10.2005 г.; Патент RU №2253877, опубликован 10.06.2005 г.). Недостатками этого способа пеленгации является малая помехоустойчивость, вследствие отсутствия статистической обработки данных, и наличие ложных пеленгов при приеме двух близких по азимуту лучей ионосферного сигнала.

Наиболее близким (прототип) к предлагаемому способу пеленгации при приеме многолучевых ионосферных сигналов является «Способ пеленгации с учетом корреляционной взаимосвязи между лучами», патент RU №2305294, МПК G01S 3/16, опубликован 27.08.2007 г.

Согласно данному способу пеленгации (прототип) последовательность действий следующая. С помощью антенной решетки, состоящей из N вибраторов, расположенных равномерно по окружности радиуса R (пространственная база сигнала) 1) принимают ионосферные сигналы, 2) преобразуют их по частоте и 3) усиливают посредством многоканального приемника. С выходов приемника аналоговые сигналы в каждом канале (от каждого вибратора) 4) преобразуют в цифровую форму посредством многоканального аналого-цифрового преобразователя (АЦП), 5) определяют амплитуды Е_0,n и фазы ψ_n принятого ионосферного сигнала в каждом канале (от каждого вибратора) с помощью временного преобразования Фурье и 6) формируют суммарную четырехмерную (для двух лучей) диаграмму направленности с учетом коэффициента корреляции между лучами по выражениям

U ^ ( α 1 ' , β 1 ' , α 2 ' , β 2 ' , ) = U ^ E n * exp ( − i k ¯ ( α 1 ' , β 1 ' ) R ¯ n ) ¯ + U ^ E n * exp ( − i k ¯ ( α 2 ' , β 2 ' ) R ¯ n ) ¯ E ^ n E ^ n * ¯ ,   ( 3 )

где

U ^ 1 = E ^ n exp ( i k ¯ 1 ( α 1 ' , β 1 ' ) R ¯ n ) ¯ + E n exp ( i k ¯ 2 ( α 2 ' , β 2 ' ) R ¯ n ) ¯ A ^ 1 − A ^ A ^ *

U ^ 2 = E ^ n exp ( i k ¯ 2 ( α 2 ' , β 2 ' ) R ¯ n ) ¯ + E ^ n exp ( i k ¯ 1 ( α 1 ' , β 1 ' ) R ¯ n ) ¯ A * ^ 1 − A ^ A ^ *

A ^ = exp ( i ( k ¯ 2 ( α 2 ' , β 2 ' ) − k ¯ ( α 1 ' , β 1 ' ) ) R ¯ n ) ¯

Ê_n - комплексная амплитуда сигнала, измеренная на n-вибраторе,

R ¯ n - радиус-вектор, определяющий местоположение n-вибратора,

k ¯ 1 ( α 1 ' , β 1 ' ) , k ¯ 2 ( α 2 ' , β 2 ' ) - волновые векторы первого и второго лучей ионосферного сигнала, зависящие от оценочных азимутов α 1 ' , α 2 ' и углов места β 1 ' , β 2 ' .

Â1 - коэффициент корреляции между лучами,

черта сверху означает суммирование по индексу n.

Знак * означает комплексное сопряжение,

знак ^ означает комплексную величину.

7) Производят сканирование диаграммой направленности в четырехмерном пространстве за счет изменения оценочных азимутов и углов места α 1 ' , α 2 ' и β 1 ' , β 2 ' в указанных угловых диапазонах с определенным шагом, запоминая значения параметров α 1 ' , α 2 ' , β 1 ' , β 2 ' , U ^ 1 , U ^ 2 , U ^ ( α 1 ' , β 1 ' , α 2 ' , β 2 ' ) .

Азимут и угол места каждого луча 8) определяют по максимуму четырехмерной диаграммы направленности.

Недостатком этого способа является его ограниченность, связанная с приемом только одного или двух лучей ионосферного сигнала. В то время как в ионосферном сигнале количество лучей может достигать четырех и более. Вторым недостатком этого способа является большая трудоемкость, связанная с необходимостью перебора (сканирования диаграммой направленности) двух азимутов и двух углов места ( α 1 ' , β 1 ' ,   и   α 2 ' , β 2 ' ) с шагом по азимуту Δα<0.5° в диапазоне 0÷360 градусов и с шагом по углу места Δβ≤0.5° в диапазоне 0÷90 градусов в четырехмерном пространстве азимутов и углов места. При увеличении количества лучей в этом способе пеленгации время, требуемое для расчета параметров, увеличивается экспоненциально. Если T необходимое время расчета параметров одного луча в одной точке области определения и M количество точек, то для N лучей требуется время T_N=T*M^2N.

Блок-схема данного способа пеленгации (прототипа) представлена на фиг.1. Согласно способу пеленгации с учетом корреляционной взаимосвязи между лучами последовательность действий следующая.

1. Принимают сигналы с помощью круговой антенной системы, состоящей из N вибраторов

( N ≥ N 1 + 1 ( 1 − | A ^ 1 | 2 ,   N 1 = 8 )

расположенных на поверхности земли равномерно по окружности радиуса R

( R ≥ 2 π 3 | k ¯ 1 ( α 01 , β 01 ) − k ¯ ( α 02 , β 02 ) | ) (блок 1)

2. С помощью многоканального приемника преобразуют сигналы от каждой антенны по частоте, усиливают и фильтруют (блок 2).

3. Преобразуют аналоговые сигналы от каждого вибратора в цифровую форму с помощью многоканального аналого-цифрового преобразователя (АЦП) (блок 3).

4. Определяют амплитуды E_n и фазы ψ_n сигналов от каждого вибратора (в каждом канале), например с помощью временного преобразования Фурье (блок 4).

5. Задают точку в пространстве оценочных азимутов α 1 ' , α 2 ' и углов места β 1 ' , β 2 ' и вычисляют согласно (3) четырехмерную диаграмму направленности U ^ ( α 1 ' , β 1 ' , α 2 ' , β 2 ' ) в заданной точке по выборке данных Ê_n и запоминают ее значения и значений переменных Û₁, Û₂, α 1 ' , β 1 ' , α 2 ' , β 2 ' (блок 5).

6. Повторяют действия блока 5 с другими значениями параметров α 1 ' , α 2 ' и β 1 ' , β 2 ' (из области их определения) с шагом по азимуту Δα≤0.5° в диапазоне 0÷360 градусов и с шагом по углу места Δβ≤0.5° в диапазоне 0÷90 градусов и создают поверхность в четырехмерном пространстве азимутов и углов места (четырехмерную диаграмму направленности) (блок 6).

7. Определяют максимальное значение четырехмерной диаграммы направленности и фиксируют параметры α 1 ' = α 01 , β 1 ' = β 01 , α 2 ' = α 02 , β 2 1 = β 02 , а также Û₁=Û₀₁, Û₂=Û₀₂ (блок 7).

8. Определяют ранг поля (однолучевое или двулучевое) по условию U₀₁/U₀₂≥3 и оставляют решения, удовлетворяющие этому условию (блок 8).

Целью данного изобретения (технический результат) является расширение возможностей «Способа пеленгации с учетом корреляционной взаимосвязи» на случай приема K лучей (K=1÷4 и более) и сокращение времени расчета угловых параметров многолучевого ионосферного сигнала.

Технический результат достигается тем, что с помощью круговой антенной системы, многоканального приемника, многоканального аналого-цифрового преобразователя (АЦП) и временного преобразования Фурье формируется пространственно-временной массив комплексных данных Ê_n,k, отображающий значения напряженности поля в n точках пространства (n - номер вибратора) и в k-моменты времени с интервалами 1-2 секунды (индекс k определяет номер временного среза данных на n вибраторах, k=1÷k). Формируется корреляционная матрица  размерностью, равной количеству лучей (K*K), элементы которой усредняются по индексу n (по вибраторам, по пространству), задаются оценочные значения азимута α' и угла места β' из области их определения и по матричному выражению (4) определяются неопределенные коэффициенты â₁÷â₄,

A ^ a ¯ = b ¯ ,   г д е   ( 4 )

 - корреляционная матрица с элементами E ^ n , k E ^ n , p * ¯ ,

k=1÷K, p=1÷K, n=1÷N, черта сверху означает суммирование по индексу n,

b ¯ = ( b ^ 1 ÷ b ^ K ) T - вектор-столбец с координатами b ^ k = exp ( − i K ¯ ( α ′ , β ′ ) R ¯ n ) E n , k * ¯ (черта сверху определяет суммирование по индексу n, по вибраторам).

ā=(â₁÷â_K)^T - вектор-столбец неопределенных коэффициентов.

Оценка неопределенных коэффициентов позволяет получить значение

нормированного функционала правдоподобия Δ(α',β') по выражению (5).

Δ ( α ' , β ' ) = 1 1 − ∑ n = 1 N ∑ k = 1 K | a ^ k E ^ n , k exp ( i K ¯ ( α ' , β ' ) R ¯ n ) |   ( 5 )

Методом перебора по азимуту α' и углу места β' создается полная поверхность функционала в двумерном пространстве углов (0÷360° по азимуту и 0÷90° по углу места). С помощью порогового значения U₀=20 выделяют K максимумов этой поверхности, по которым определяют оценочные значения азимутов и углов места K лучей ионосферного сигнала.

Существенные отличия предлагаемого способа пеленгации от прототипа следующие.

- Исключается операция создания четырехмерной диаграммы направленности и сканирование этой диаграммой в четырехмерном пространстве, которая значительно увеличивает время расчета параметров ионосферного сигнала и не позволяет реализовать способ (прототип) с большим количеством лучей.

- Пространственная информация, получаемая с помощью антенной системы, дополняется необходимой информацией во времени (срезы данных) и проводится наиболее оптимальная совместная пространственно - временная обработка данных.

- Вместо оценок параметров лучей по максимуму четырехмерной диаграммы направленности в прототипе, в предлагаемом способе производятся оценки параметров лучей по максимумам функционала правдоподобия (количество максимумов совпадает с количеством лучей) в двумерном пространстве азимутов и углов места.

Обоснованием способа пеленгации ионосферного сигнала в условиях интерференции лучей является следующее.

Запишем сигнал на n-вибраторе и в k-точке по времени Ê_n,k в комплексной форме в виде

E ^ n , k = ∑ m M U ^ m e i ( ω m t k − K ¯ m ( α 0, m , β 0, m ) R ¯ n )   ( 6 )

где Û_m - комплексная амплитуда m-луча ионосферного сигнала,

K ¯ m ( α 0, m , β 0, m ) - волновой вектор m-луча ионосферного сигнала,

α_0,m,β_0,m - значения азимута и угла места m-луча ионосферного сигнала,

R ¯ n - местоположение n-вибратора,

t_k - время отсчетов напряженности поля (k меняется в пределах от 1 до K, K=М - количество лучей в ионосферном сигнале,

ω_m - круговая частота m-луча ионосферного сигнала.

Используя временную последовательность данных, исключим переменные, описывающие поля М-1 луча

( U ^ m , K ¯ m ( α 0, m , β 0, m ) , ω m ) .

В результате получим выражение (7) с неопределенными коэффициентами â₁÷â_K, выражение в правой части которого описывает поле лишь одной волны с единичной амплитудой (индекс т у переменных убран).

∑ k = 1 K a ^ k E ^ n , k = e − i K ¯ ( α 0 , β 0 ) R ¯ n   ( 7 )

Неопределенные коэффициенты â₁÷â_K не зависят от номера вибратора n. Они зависят лишь от временного интервала Δt. Следовательно они одинаковы для выражения (7) при разных значениях индекса n. На основании этого можно проводить статистическую обработку пространственных данных методом максимального правдоподобия для нахождения значений неопределенных коэффициентов. Для этого запишем функционал (8).

Δ 1 ( α ' , β ' ) = ∑ n = 1 N ∑ k = 1 K | a ^ k E ^ n , k − e − i K ¯ ( α ' , β ' ) R ¯ n | 2   ( 8 )

В этом выражении штрихами обозначены оценочные значения азимута и угла места. Дифференцируя выражение (8) по неопределенным коэффициентам â₁÷â_K и приравнивая дифференциалы нулю, получим матричное уравнение (4).

A ^ * a ¯ = b ¯

где Â - корреляционная матрица, элементы которой определяются значениями поля на вибраторах E ^ n , k E ^ n , p * ¯ .

По индексу n производится суммирование (черта сверху), индексы k=1÷K, p=1÷K определяют размерность матрицы.

ā=(â₁÷â_K)^T - вектор столбец неопределенных коэффициентов.

b ¯ = ( b 1 ÷ b K ) T - вектор столбец, коэффициентами которого являются выражения

b K = exp − ( − i K ¯ ( α ' , β ' ) R ¯ n E ^ n , k * ¯

Задавая оценочные значения α', β' из области определения (0-360° по азимуту и 0÷90° по углу места) можно решить матричное уравнение (4) и определить неопределенные коэффициенты â₁÷â_K. Подставляя их в функционал правдоподобия (8), можно получить точку поверхности этого функционала. Перебирая все значения оценочных углов α',β' из области их определения, и повторяя расчет коэффициентов â₁÷â_K и функционала (8), можно получить всю поверхность функционала. Минимумы этой поверхности определяют решения. Для удобства функционал Δ1(α', β') (8) можно преобразовать в нормированный функционал (5).

Δ ( α ' , β ' ) = 1 1 − ∑ n = 1 N ∑ k = 1 K | a ^ k E ^ n , k exp ( i K ¯ ( α ' , β ' ) R ¯ n ) |

В этом функционале решения определяют его максимумы, значения которых меняются от 1 до бесконечности в зависимости от дисперсии шума. При условии, что отношение сигнал/шум равно 20 дБ, пороговым значением U₀, отделяющим значения максимумов от шумовых максимумов, является U₀=20. Таким образом, максимумы, превышающие пороговое значение U_0, определяют K решений:

α k ' = α 0, k ,   β k ' = β 0, k

В случае, если в принятом ионосферном сигнале количество лучей меньше предполагаемого, то для лишних лучей максимум функционала будет на уровне шумовых максимумов и за счет установленного порога они исключаются.

Сущность предлагаемого способа пеленгации ионосферных сигналов в условиях интерференции лучей поясняется следующими чертежами.

На фиг.1 представлена структурная схема устройства, с помощью которого реализуется прототип «Способ пеленгации с учетом корреляционной взаимосвязи между лучами».

На фиг.2 представлена структурная схема устройства, с помощью которого реализуется предлагаемый способ пеленгации. По сравнению с прототипом первые четыре блока идентичны, вместо 5÷8 блоков прототипа предлагаются действия новых блоков 5÷10. С помощью этих блоков формируется пространственно-временной массив, который преобразуется с помощью неопределенных коэффициентов (7), и методом максимального правдоподобия производится оценка угловых параметров многолучевого ионосферного сигнала.

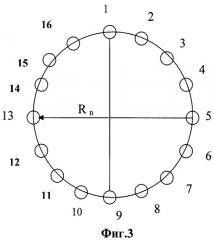
На фиг.3 показано расположение антенн на поверхности земли, составляющих круговую антенную систему. Количество вибраторов равно 16, радиус антенной системы равен 65 м.

На фиг.4 показан схематично пространственно-временной массив, получаемый в блоке 5. Количество вибраторов N, количество временных срезов данных K, полученных через интервал времени Δt=1÷2 с.

На фиг.5 показана поверхность функционала правдоподобия Δ(α',β') (Delta) в зависимости от азимута α' (Alfa) и угла места β' (Beta). Четыре максимума поверхности функционала определяют азимуты и углы места четырех лучей ионосферного сигнала. Поверхность функционала правдоподобия получена с помощью модельных расчетов, в которых принято количество лучей K=4 с угловыми параметрами лучей, представленных в Таблице 1 (верхние две строки). Нижние две строки таблицы определяют найденные с помощью максимумов поверхности функционала правдоподобия, азимуты и углы места четырех лучей.

Таблица 1
αβ°	№1	№2	№3	№4
α,°	70	68	66	64
β,°	40	13	25	30
α',°	70.12	68.12	67.12	64.12
β',°	40	12	20	30

Значения полученных с помощью предлагаемого способа пеленгации азимутов и углов места четырех лучей вполне соответствуют их модельным значениям.

На фиг.6. показана поверхность функционала правдоподобия, полученная с помощью модельных расчетов при следующих условиях. В модели задан ионосферный сигнал с двумя лучами. Расчет поверхности функционала проведен четырехлучевым алгоритмом. Максимумы двух лишних лучей не превышают уровня шумовых максимумов (на чертеже не видны). Следовательно, предлагаемый способ локации вполне работоспособен в случаях приема ионосферного сигнала с одним, двумя, тремя и четырьмя лучами.

На фиг.7 показаны углы места многолучевого ионосферного сигнала, полученные с помощью восьмиканального пеленгатора, работающего по алгоритму предлагаемого способа пеленгации. С помощью пеленгатора ведется прием сигналов станции Москва (РВМ) на частоте f=9,996 МГц в течение 22 с. Отмечается наличие как двухлучевой структуры ионосферного сигнала, так и трехлучевой структуры. Получить такие оценки углов места с помощью классических методов пеленгации не представляется возможным.

Предлагаемый способ пеленгации ионосферных сигналов в условиях интерференции лучей осуществляется следующим образом (фиг.2).

1. Принимают сигналы с помощью круговой антенной системы, состоящей из N вибраторов, расположенных на поверхности земли равномерно по окружности радиуса R (блок 1).

2. С помощью многоканального приемника преобразуют сигналы от каждой антенны по частоте, усиливают и фильтруют (блок 2).

3. Преобразуют аналоговые сигналы от каждого вибратора в цифровую форму с помощью многоканального аналого-цифрового преобразователя (АЦП) (блок 3).

4. Определяют амплитуды E_n и фазы ψ_n сигналов от каждого вибратора (в каждом канале), например, с помощью временного преобразования Фурье (блок 4).

5. Повторяя действия в блоках 1÷4 K раз (K - количество лучей ионосферного сигнала), через интервалы времени Δt=1÷2 с формируют пространственно-временной массив данных E_n,k, ψ_n,k (k=1÷K, номер среза данных на вибраторах) (блок 5).

6. Формируют корреляционную матрицу данных с элементами E ^ n , k E ^ n , p * ¯ , (k=1÷k, p=1÷k, n=1÷N). Черта сверху определяет суммирование по индексу n (блок 6).

7. Задают точку в области определения оценочных углов α',β' и вычисляют неопределенные коэффициенты â₁÷â₄ по матричному уравнению (4), с помощью которых вычисляют значение функционала правдоподобия (5) (блок 7).

Δ ( α ' , β '