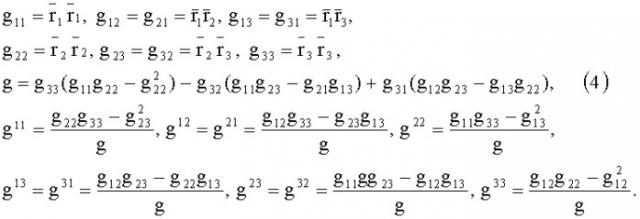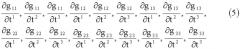Способ параметризации локальных углублений на цилиндрических телах и устройство для его осуществления

Способ параметризации локальных углублений на цилиндрических телах и устройство для его осуществления

Иллюстрации

Показать все

Реферат

Изобретение относится к отраслям, связанным с моделированием цилиндрических тел с локальными углублениями сложной формы, такими как дефекты, вырезы и конструктивные выемки на поверхности рассматриваемых тел, в частности, деталей машин, трубопроводов различного назначения, корпусов реакторов и емкостей, транспортных средств, космической техники, элементов строительных конструкций и сооружений, приборов и оборудования и др.

Известны способы определения кривизны и уклонов профиля поверхности дорожного покрытия в двух различных направлениях, включающие измерение параметров движения автомобиля, определение и корректировку базиса отсчета относительно плоскости, анализ упомянутых данных с помощью ЭВМ, нахождение уклонов дорожного покрытия в двух различных направлениях и выдачу на экран монитора измерительно-вычислительного комплекса расчетных параметров в процессе движения автомобиля (патент РФ №2114391, М.Кл. G01C 7/04, опубл. 27.06.1998) (аналог).

Однако известные способы не позволяют осуществлять математическое моделирование цилиндрических тел в трехмерной постановке.

Имеются экспериментальные способы параметризации минимальных поверхностей, основанные на решении двухмерного уравнения Лапласа (на примере постановки внутренней задачи Дирихле, когда известны краевые значения координат и необходимо найти внутренние), в котором выставляют вертикальные стержни на необходимую высоту относительно опорной плоскости согласно требованиям задачи, с помощью измерительного прибора выверяют точность установки стержней, посредством фиксатора закрепляют стержни на необходимой высоте, натягивают на вертикальные стержни заранее изготовленную сеть из гибкого эластичного материала, с помощью высокоточного измерительного прибора замеряют высотные координаты во внутренних точках (точках пересечения) эластичной гибкой сети (патент РФ №2121166, М.Кл. G09В 23/04, опубл. 27.10.1998) (аналог).

Указанные способы не позволяют получать непрерывные и гладкие контуры при моделировании цилиндрических тел с локальными нарушениями формы поверхности.

Известен также экспериментальный способ параметризации минимальных поверхностей со сложным контуром, включающий операции фиксации гибкого элемента относительно основания, натягивания на него заранее изготовленной сети из эластичного материала, замера координат узловых точек сети относительно основания, согласно которому изготавливают пространственный каркас из криволинейных формообразующих элементов, натягивают на каркас первоначально прямоугольную в плане сеть из эластичного материала, причем каждую узловую контурную точку сети закрепляют на соответствующих точках каркаса, распределенных по длине формообразующего элемента по определенной закономерности. При этом поверхность формируют и параметризируют по узловым точкам сети относительно выбранной системы координат, выполняют обработку полученных результатов с определением компонент метрики поверхности (патент РФ №2374697, М.Кл. G09В 23/04, опубл. 27.11.2009) (прототип).

Указанный способ обладает следующими недостатками:

а) способ не предназначен для моделирования исследуемого тела в трехмерной постановке и не предполагает определение параметров цилиндрического тела в трехмерной системе координат;

б) способ не позволяет достоверно описать контуры локальных изменений формы на цилиндрических поверхностях, исходя из требований построения гладких непрерывных линий;

в) в способе не предусмотрено вычисление метрики внутренних узловых точек изучаемого тела (компонент метрического тензора).

Известны координатомеры для измерений прямоугольных координат точек, представляющие собой прозрачную пластмассовую пластинку с квадратным или прямоугольным вырезом, по краям которого нанесены шкалы (Политехнический словарь. Гл. ред. И.И.Артоболевский, М., Советская Энциклопедия, 1977. Стр. 229) (аналог).

Однако такие координатомеры не позволяют измерять пространственные координаты.

Известен также пространственный координатор, содержащий корпус с направляющими, ползуны, звенья с прорезями, кинематически связанные с осями ползунов, задатчик линейного перемещения, рычажный механизм в виде двух прямоугольных рычагов и угловые шкалы, при этом он снабжен неподвижной осью, связанной звеном с прорезью с двумя направляющими ползунов и с одним из плеч каждого из двух прямоугольных рычагов, вершина первого из двух рычагов шарнирно связана с ползунами, расположенными на плечах второго прямоугольного рычага, а ось одного из ползунов второго рычага выполнена в виде полого тела, в котором установлен подпружиненный палец с острием конической формы (патент РФ №2010148, М.Кл. G01В 5/00, опубл. 30.03.1994) (прототип).

Указанное устройство обладает следующими недостатками:

а) устройство включает в себя большое количество звеньев и поэтому является сложным и ненадежным в работе;

б) чрезмерная подвижность звеньев снижает точность измерений координат.

Задачами (целью) изобретения являются получение возможности моделирования цилиндрических тел с локальными нарушениями формы поверхности в трехмерной постановке, повышение достоверности описания формы локальных изменений на цилиндрических поверхностях и повышение точности определения метрики точек в областях отклонения формы поверхности от цилиндрической, упрощение и повышение надежности устройства.

Указанные задачи достигаются тем, что в способе параметризации локальных углублений на цилиндрических телах, включающем операции формирования исследуемой поверхности и координатной сети на ней по определенной закономерности, замера координат узловых точек сетки относительно поверхности отсчета, параметризации по узловым точкам сети относительно выбранной системы координат, обработки полученных результатов с определением компонент метрики поверхности, получают трехмерный слепок локального углубления с прилегающей областью цилиндрической поверхности, фиксируют слепок на координатно-измерительном устройстве, задают в цилиндрической системе координат сеть разбиения области замера координат поверхности слепка по углу и по образующей в заданной закономерности, например, точках интегрирования по Гауссу. При этом учитывают размеры слепка и характер предполагаемого разбиения на конечные элементы. Замеряют радиальные координаты узловых точек сети на поверхности слепка для заданного разбиения, вычисляют компоненты метрики поверхности, назначают необходимое число расчетных слоев по толщине цилиндрического тела в соответствии с выбранной схемой интегрирования и числом конечных элементов по толщине, определяют расчетные координаты сети для слоев с учетом координат поверхности углубления. Угловой сектор дефектной области в градусах определяют по формуле

α d e f = 360 ⋅ b d e f π ⋅ D ,

где b_def - размер дефекта по угловой координате, замеренный по окружности цилиндрического тела;

D - диаметр цилиндрического тела.

Далее вычисляют параметры метрики и при необходимости определяют напряженно-деформированное состояние цилиндрического тела с локальными углублениями, например, используя метод конечных элементов.

Радиус-вектор произвольной точки дефектного участка цилиндрического тела задают в виде:

r ¯ = [ R в н ( 1 − t 1 ) + R t 1 ] e ¯ 1 ( t 2 ) + ( H н + L d e f t 3 ) k ¯ ,

e ¯ 1 ( t 2 ) = cos α ( t 2 ) i ¯ + sin α ( t 2 ) j ¯ ,

где R_вн - внутренний радиус цилиндрического тела;

R - радиус поверхности дефектного участка, совпадающий в узловых точках разбиения с радиальными координатами R_jk,

i ¯ , j ¯ , k ¯ - единичные орты в декартовой системе координат;

Н_н - начало дефектного участка цилиндрического тела по оси z;

h - толщина стенки цилиндрического тела в конкретной точке;

L_def - длина дефектного участка цилиндрического тела.

В устройстве для осуществления способа параметризации локальных углублений на цилиндрических телах, включающем корпус с направляющими, задатчик линейного перемещения, угловую шкалу и инструменты для замера координат, корпус имеет координатно- измерительный стол для фиксации слепка и стойки, на которых размещен направляющий вал с указателем углового перемещения и фиксатором. На валу установлена каретка с возможностью продольного перемещения. Сечение вала в рабочей части имеет форму, например, или квадрата, или прямоугольника, или треугольника, или с прорезью, или со шпонкой, исключающую поворот каретки относительно вала. Каретка имеет указатель линейного перемещения каретки вдоль вала. На каретке закреплен линейный измеритель. Линейный измеритель может быть выполнен в виде лазерного дальномера, ультразвукового сканера или, в простейшем случае в виде измерительного индикатора. Указатели углового и линейного перемещений могут быть оптического (например, лазерного) или стрелочного типа. Кроме того, в состав устройства входит комплект приспособлений для снятия слепка. Приспособление для снятия слепка выполнено в виде рамки из двух пар пластин, образующих боковые поверхности усеченной прямоугольной пирамиды. Пластины первой пары имеют прямоугольную форму, а пластины второй пары имеют форму равнобедренной трапеции, меньшее основание которой имеют криволинейную форму, совпадающую с контуром направляющей линии ненарушенного участка цилиндрического тела. Кроме того, в комплекте устройства имеется набор подкладок под рамки для перестройки устройства для различных радиусов цилиндрического тела.

На фиг.1 представлен фрагмент цилиндрического тела с локальным углублением; на фиг.2 приведена схема размещения на цилиндрическом теле приспособления для снятия слепка; на фиг.3 - то же, вид А; на фиг.4 - расчетная схема слоев дефектной области; на фиг.5 представлена схема устройства для осуществления способа параметризации локальных углублений, общий вид, на фиг.6 - то же, вид сбоку; на фиг.7 показано приспособление для снятия слепка; на фиг.8 представлены обозначения координаты точек для одного сечения: R_i - радиальная координата, α_i - угловая координата для i-той точки в рассматриваемом сечении z_k; на фиг.9 и 10 представлены фотографии, соответственно, углубления на поверхности цилиндрического тела и слепка от него.

Способ параметризации локальных углублений на цилиндрических телах осуществляют следующим образом.

Предварительно подготавливают область ABCF расположения углубления abcf (это могут быть различного рода дефекты, повреждения, технологические выемки и т.д.) на цилиндрическом теле для процедуры снятия (формования) слепка. Для этого очищают поверхность исследуемого цилиндрического тела на рассматриваемом участке, удаляют инородные включения, слои ржавчины или покрытий. При необходимости наносят антиадгезионный состав (производят смазку дефектного участка антиадгезионной жидкостью, напыляют порошок или иное вещество), что необходимо для сохранения целостности слепка при его снятии после формования. Далее накладывают на место расположения углубления с прилегающей к нему областью приспособление для снятия слепка. При необходимости приспособление для снятия слепка прикрепляют к цилиндрическому телу при помощи фиксаторов (на фигурах не показаны). Заполняют приспособление формовочным материалом (например, гипсом, алебастром или другим формирующим составом), выдерживают формующий состав до затвердевания, освобождают (разъединяют) фиксаторы крепления приспособления к цилиндрическому телу и получают трехмерный слепок локального углубления с прилегающей ненарушенной областью цилиндрической поверхности.

Полученный слепок совместно с приспособлением для снятия слепка фиксируют на координатно-измерительном столе устройства (слепок извлекают из приспособления для снятия слепка только при необходимости). Задают сеть разбиения области поверхности слепка для замера координат в цилиндрической системе координат по углу и по образующей по заданной закономерности. Разбивку осуществляют с выбором одного из двух типов: первый тип - равномерная разбивка, второй тип - разбивка по заданной закономерности, например, по точкам интегрирования по Гауссу. При этом учитывают размеры слепка и характер предполагаемого разбиения на конечные элементы.

Угловой сектор α_def дефектной области в градусах определяют по формуле

α d e f = 360 ⋅ b d e f π ⋅ D ,

где b_def - размер дефекта по угловой координате, замеренный по окружности цилиндрического тела;

D - диаметр цилиндрического тела.

Замеряют радиальную координату каждой узловой точки заданной сети на поверхности слепка. В частности, согласно сети разбиения выбирают сечение, для которого замеряют радиальные координаты для всех рассматриваемых угловых координат. Далее переходят к другому сечению и выполняют аналогичную процедуру замеров. Таким образом, для каждого выбранного сечения z_k (k=1, 2, 3, …, р) и угловой координаты α_j (j=1, 2, 3, …, m) получают радиальные координаты R_jk узлов разбиения на поверхности слепка.

Далее приступают к процедуре параметризации рассматриваемого тела. Параметризацию дефектного участка цилиндрического тела по рассматриваемой сети разбиения производят параметрами t¹, t² и t³ единичного куба. При этом параметром t¹ задают радиальные координаты r, параметром t² - угловые координаты α, параметром t³ - координаты сечения по оси z.

Радиус-вектор r ¯ произвольной точки М дефектного участка цилиндрического тела задают через параметры t¹, t², t³ в виде:

r ¯ = [ R в н ( 1 − t 1 ) + R t 1 ] e ¯ 1 ( t 2 ) + ( H н + L d e f t 3 ) k ¯ ,

e ¯ 1 ( t 2 ) = cos α ( t 2 ) i ¯ + sin α ( t 2 ) j ¯ ,                               ( 2 ) ,

где R_вн - внутренний радиус цилиндрического тела;

R - радиус поверхности дефектного участка, совпадающий в узловых точках разбиения с радиальными координатами R_jk;

i ¯ , j ¯ , k ¯ - единичные орты в декартовой системе координат;

Н_н - начало дефектного участка цилиндрического тела по оси z;

h - толщина стенки цилиндрического тела в конкретной точке;

L_def - длина дефектного участка цилиндрического тела.

После определения радиальных координат R_ij в узловых точках разбиения на поверхности слепка задают радиальные координаты по толщине (по слоям) цилиндрического тела в дефектной области, в зависимости от числа заданных расчетных слоев, сохраняя пропорцию размеров разбивки слоев в дефектной и недефектной областях по толщине (фиг.4). Необходимое число расчетных слоев по толщине реального цилиндрического тела назначают согласно выбранной схемы интегрирования и числа конечных элементов по толщине цилиндрического тела. Вычисляют радиальные координаты расчетных слоев.

Далее производят расчет параметров метрики по следующему алгоритму:

1. Дифференцируют выражение (1) по t¹, t² и t³ и определяют координатные векторы r ¯ 1 , r ¯ 2 и r ¯ 3 :

r ¯ 1 = ∂ r ¯ ∂ t 1 ,   r ¯ 2 = ∂ r ¯ ∂ t 2 ,     r ¯ 3 = ∂ r ¯ ∂ t 3 .                                   ( 3 ) ,

2. Определяют ковариантные g₁₁, g₁₂, g₁₃, g₂₁, g₂₂, g₂₃, g₃₁, d₃₂, g₃₃ и контравариантные g¹¹, g¹², g¹³ g²¹, g²², g²³ g³¹, g³², g³³ компоненты первого основного метрического тензора и фундаментальный определитель g:

g 11 = r ¯ 1 r ¯ 1 ,       g 12 = g 21 = r ¯ 1 r ¯ 2 ,     g 13 = g 31 = r ¯ 1 r ¯ 3 , g 22 = r ¯ 2 r ¯ 2 ,     g 23 = g 32 = r ¯ 2 r ¯ 3 ,       g 33 = r ¯ 3 r ¯ 3 ,   g = g 33 ( g 11 g 22 − g 22 2 ) − g 32 ( g 11 g 23 − g 21 g 13 ) + g 31 ( g 12 g 23 − g 13 g 22 ) ,                   ( 4 ) g 11 = g 22 g 33 − g 23 2 g ,     g 12 = g 21 = g 12 g 33 − g 23 g 13 g ,     g 22 = g 11 g 33 − g 13 2 g , g 13 = g 31 = g 12 g 23 − g 22 g 13 g ,     g 23 = g 32 = g 11 g g 23 − g 12 g 13 g ,     g 33 = g 12 g 22 − g 12 2 g .

3. Дифференцируя ковариантные компоненты первого основного метрического тензора (4) по t¹, t² и t³, определяют их первые производные:

∂ g 11 ∂ t 1 ,   ∂ g 11 ∂ t 2 ,   ∂ g 11 ∂ t 3 ,   ∂ g 12 ∂ t 1 ,   ∂ g 12 ∂ t 2 ,   ∂ g 12 ∂ t 3 ,   ∂ g 13 ∂ t 1 ,   ∂ g 13 ∂ t 2 ,   ∂ g 13 ∂ t 3 ,                               ( 5 ) ∂ g 22 ∂ t 1 ,   ∂ g 22 ∂ t 2 ,   ∂ g 22 ∂ t 3 ,   ∂ g 23 ∂ t 1 ,   ∂ g 23 ∂ t 2 ,   ∂ g 23 ∂ t 3 ,   ∂ g 33 ∂ t 1 ,   ∂ g 33 ∂ t 2 ,   ∂ g 33 ∂ t 3

4. Определяют символы Кристоффеля второго рода по формулам:

Г 11 1 = 1 2 g 11 ( ∂ g 11 ∂ t 1 +   ∂ g 11 ∂ t 1 −   ∂ g 11 ∂ t 1 ) + 1 2 g 12 ( ∂ g 12 ∂ t 1 +   ∂ g 12 ∂ t 1 −   ∂ g 11 ∂ t 2 ) + 1 2 g 13 ( ∂ g 13 ∂ t 1 +   ∂ g 13 ∂ t 1 −   ∂ g 11 ∂ t 3 ) , Г 12 1 = 1 2 g 11 ( ∂ g 11 ∂ t 2 +   ∂ g 21 ∂ t 1 −   ∂ g 12 ∂ t 1 ) + 1 2 g 12 ( ∂ g 12 ∂ t 2 +   ∂ g 22 ∂ t 1 −   ∂ g 12 ∂ t 2 ) + 1 2 g 13 ( ∂ g 13 ∂ t 2 +   ∂ g 23 ∂ t 1 −   ∂ g 12 ∂ t 3 ) , Г 13 1 = 1 2 g 11 ( ∂ g 11 ∂ t 3 +   ∂ g 31 ∂ t 1 −   ∂ g 13 ∂ t 1 ) + 1 2 g 12 ( ∂ g 12 ∂ t 3 +   ∂ g 32 ∂ t 1 −   ∂ g 13 ∂ t 2 ) + 1 2 g 13 ( ∂ g 13 ∂ t 3 +   ∂ g 33 ∂ t 1 −   ∂ g 13 ∂ t 3 ) , Г 12 2 = 1 2 g 21 ( ∂ g 11 ∂ t 1 +   ∂ g 11 ∂ t 1 −   ∂ g 11 ∂ t 1 ) + 1 2 g 22 ( ∂ g 12 ∂ t 1 +   ∂ g 12 ∂ t 1 −   ∂ g 11 ∂ t 2 ) + 1 2 g 23 ( ∂ g 13 ∂ t 1 +   ∂ g 13 ∂ t 1 −   ∂ g 11 ∂ t 3 ) , Г 12 2 = 1 2 g 21 ( ∂ g 11 ∂ t 2 +   ∂ g 21 ∂ t 1 −   ∂ g 12 ∂ t 1 ) + 1 2 g 22 ( ∂ g 12 ∂ t 2 +   ∂ g 22 ∂ t 1 −   ∂ g 12 ∂ t 2 ) + 1 2 g 23 ( ∂ g 13 ∂ t 2 +   ∂ g 23 ∂ t 1 −   ∂ g 12 ∂ t 3 ) , Г 13 2 = 1 2 g 21 ( ∂ g 11 ∂ t 3 +   ∂ g 31 ∂ t 1 −   ∂ g 13 ∂ t 1 ) + 1 2 g 22 ( ∂ g 12 ∂ t 3 +   ∂ g 32 ∂ t 1 −   ∂ g 13 ∂ t 2 ) + 1 2 g 23 ( ∂ g 13 ∂ t 3 +   ∂ g 33 ∂ t 1 −   ∂ g 13 ∂ t 3 ) , Г 11 3 = 1 2 g 31 ( ∂ g 11 ∂ t 1 +   ∂ g 11 ∂ t 1 −   ∂ g 11 ∂ t 1 ) + 1 2 g 32 ( ∂ g 12 ∂ t 1 +   ∂ g 12 ∂ t 1 −   ∂ g 11 ∂ t 2 ) + 1 2 g 33 ( ∂ g 13 ∂ t 1 +   ∂ g 13 ∂ t 1 −   ∂ g 11 ∂ t 3 ) , Г 12 3 = 1 2 g 31 ( ∂ g 11