Способ определения параметров широкополосного сигнала

Способ определения параметров широкополосного сигнала

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области систем обработки информации и измерительной техники и может быть использовано для оценки параметров широкополосного синусоидального сигнала (амплитуды U₀, начальной фазы φ₀ и частоты ω₀). В случае широкополосного синусоидального сигнала на интервалах измерения укладывается лишь небольшое количество периодов колебаний вплоть до одного или даже части периода, в результате чего ширина спектра сигнала Δω оказывается порядка несущей частоты ω₀ (широкополосные сигналы) /1, стр.121, 2 стр.36, 3/. Такое положение может быть в локации, при использовании пониженной несущей частоты зондирующего импульса, в системах связи, в радиофизических и радиотехнических комплексах аппаратуры при использовании широкополосных сигналов.

Широко известны способы оценки параметров синусоидального сигнала с помощью спектрального анализа в системах обработки информации и в измерительной технике. В этом случае используют аналоговый или цифровой узкополосный фильтр, частота которого перестраивается в определенной частотной области. Максимум амплитудно-частотной характеристики, полученной с помощью этого фильтра, определяет несущую частоту сигнала ω=ω₀, значение максимума определяет амплитуду U₀, значение фазо-частотной характеристики в точке ω=ω₀ определяет начальную фазу сигнала φ₀ /1, 2, 4/, (Патент RU №2137143 от 10.09.1999 г; Патент RU №2229725 от 27.05.2004 г.; Патент RU №2399919 от 20.09.2010; патент РФ 2276375 от 10.05.2006, патент Рф 2133041 от 10.07.1999 г.). К недостаткам способов оценок параметров сигналов на основе спектрального анализа можно отнести то, что они могут использоваться лишь для узкополосных сигналов. С увеличением широкополосности сигнала ширина его спектра значительно увеличивается и точности оценок параметров понижаются.

Известны способы измерения параметров синусоидального сигнала по аналитическим выражениям, получаемым по нескольким временным отсчетам сигнала (Заявка РФ 93057353/09 от 24.12.1993 г., заявка РФ 94038816 от 27.05.1997 г.). В этом случае записывается система алгебраических уравнений для разных моментов времени. Ее решение позволяет получить оценки параметров широкополосного сигнала. К недостаткам этих способов оценки параметров можно отнести то, что вследствие ограниченного количества временных отсчетов (количество отсчетов определяется количеством неизвестных параметров сигнала), помехоустойчивость оказывается невысокой. Отсутствует статистическое усреднение. Использование дополнительных отсчетов сигнала при наличии шумовой добавки приводит к системе несовместных алгебраических уравнений.

В описании к патенту №2117306 от 10.08.1998 достигаемым техническим результатом является устранение зависимости точности определения частоты узкополосного сигнала от его длительности. Задача частично эквивалентна задаче настоящей заявки, однако решение ее связано с решением системы двух уравнений, составленных для двух смежных точек дискретного спектра с учетом малости частотного различия и, вследствие этого, помехоустойчивость способа оценки параметров сигнала оказывается низкой.

В описании к патенту №2430382 от 16.12.2008 г. «Способ оценки параметров широкополосных сигналов по методу Прони» решается задача оценки параметров полигармонического сигнала методом Прони в сочетании со спектральным методом. Недостатком является переход от выборки данных к разностному уравнению, что снижает эффективность обработки. Кроме того, метод Прони неустойчив при малых отношениях сигнал/шум. Он может давать ложные решения при малом интервале дискретизации Δt.

Известные методы сверхразрешения типа Прони, предсказаний, «Music», Писаренко, и ряд других методов, хорошо представленных в /4/, позволяют получать оценки частоты широкополосных сигналов. Они могли бы быть основой для оценок параметров широкополосного сигнала. Однако эти методы не имеют достаточного теоретического обоснования. Они основаны на анализе разностного уравнения, при переходе к которому от принятого сообщения отношение сигнал/шум уменьшается. Кроме того, при малых значениях дискретизации At (в широкополосных сигналах Δt мало в соответствии с теоремой Котельникова) могут появляться ложные решения. Точность оценок параметров широкополосных сигналов оказывается невысокой.

Известен ряд способов измерения частоты синусоидальных сигналов /5, 6/.Однако они не являются статистически оптимальными с точки зрения измерения частоты синусоидальных сигналов на фоне шумов /7, 8/.Они могут использоваться лишь для узкополосных сигналов.

Известен способ измерения частоты синусоидальных сигналов, основанный на использовании разностно-фазовой статистики сигнала (Патент на изобретение РФ №2183839, Способ измерения частоты синусоидальных сигналов и устройство для его реализации, М., ФИПС, 2002 г.) В этих способах не рассматривается вопрос получения разности фаз. Оптимальным для оценки фазы является косинусное и синусное преобразование Фурье. В связи с этим эти методы могут использоваться лишь для узкополосных сигналов.

Наиболее близким к предлагаемому изобретению является способ определения параметров синусоидального сигнала с помощью дискретного спектрального анализа /2, стр.250, формула в комплексном виде (5.3), стр.142/. Его основой является следующее. Запишем выборку данных E_n в виде

E n = U 0 cos ( ω 0 t n + ϕ )                                                                                                           ( 1 )

где U₀ - амплитуда сигнала,

ω₀ - круговая частота сигнала,

φ - начальная фаза сигнала,

t_n - момент времени.

Применим к выборке данных E_n дискретное синусное и косинусное преобразование Фурье. При непрерывном изменении частоты получим квадратурные компоненты A(ω), B(ω), зависящие от частоты ω.

A ( ω ) = E n cos ( ω t n ) ¯ , B ( ω ) = E n sin ( ω t n ) ¯                                                       ( 2 )

где черта сверху (и далее по тексту) означает суммирование по индексу «n» в пределах 1÷N.

E_n - выборка дискретных данных, полученная на интервале времени T с дискретностью Δt.

При получении квадратурных компонент используется условие узкополосности сигнала, т.е. интервал времени Т должен быть много больше периода синусоидальных колебаний T>2π/ω₀. Оно сводится к тому, что

cos 2 ( ω t n ) ¯ ≈ sin 2 ( ω t n ) ¯ ≈ 1 / 2,   cos ( ω t n ) sin ( ω t n ) ¯ ≈ 0.                                                       ( 3 )

Преобразуя квадратурные компоненты, получим амплитудно-частотный U(ω) и фазо-частотный φ(ω) спектры.

U ( ω = ω 0 ) = 2 A ' ( ω 0 ) 2 + B ' ( ω 0 ) 2 ,   φ ( ω ) = − a r c t g ( B ( ω ) A ( ω ) )                                         ( 4 )

Максимум амплитудно-частотного спектра определяет измеряемую частоту ω=ω₀. Значение максимума определяет амплитуду сигнала U₀, а значение фазы на частоте ω=ω₀ определяет начальную фазу сигнала φ. Таким образом, амплитуду, начальную фазу и частоту синусоидального сигнала оценивают с помощью дискретного преобразования Фурье.

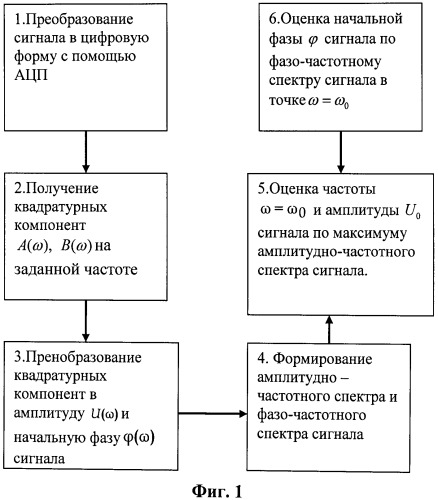
Данный способ оценки параметров синусоидального сигнала, принятый нами за прототип, осуществляют в устройстве, блок-схема которого показана на фиг.1.

1. Аналоговый сигнал преобразуют в дискретную входную последовательность с интервалом дискретизации Δt в соответствии с теоремой Котельникова об отсчетах с помощью аналого-цифрового преобразователя (АЦП).

2. На заданной частоте ω согласно выражениям (1) проводят синусное и косинусное преобразование Фурье и получают квадратурные компоненты A(ω), B(ω).

3. Преобразуют полученные квадратурные компоненты A(ω), B(ω) в амплитуду и фазу сигнала по выражениям (4).

4. Перебирая частоты в заданном диапазоне и каждый раз выполняя действия 1-3, формируют амплитудно-частотный U(ω) и фазо-частотный φ(ω) спектры.

5. По максимуму амплитудно-частотного спектра U(ω=ω₀) определяют оценку частоты ω=ω₀ и амплитуды сигнала U₀.

6. По фазо-частотному спектру в точке ω=ω₀ определяют оценку начальной фазы сигнала φ.

К недостаткам этого способа оценки параметров синусоидального сигнала можно отнести то, что с уменьшением интервала T значения cos 2 ( ω t n ) ¯ и sin 2 ( ω t n ) ¯ уже не равны ½, а значения cos ( ω t n ) sin ( ω t n ) ¯ уже не равны нулю. Кроме того, с уменьшением интервала обработки T увеличивается ширина амплитудно-частотного спектра, а следовательно, и погрешности оценки параметров синусоидального сигнала.

Целью предлагаемого способа (технический результат) является повышение точности оценки параметров широкополосных синусоидальных сигналов, что расширяет функциональные возможности радиотехнических комплексов аппаратуры. Поставленная цель достигается тем, что в способе определения параметров широкополосного синусоидального сигнала уточняются значения квадратурных компонент A(ω), B(ω) с помощью поправочных коэффициентов a(ω) b(ω) c(ω).

Черта сверху означает суммирование по индексу n.

В результате получаем уточненные квадратурные компоненты A′(ω), B′(ω).

Оценка частоты ω и квадратурных компонент сигнала A′(ω), B′(ω) производятся не по максимуму спектральной линии сигнала (ширина ее увеличивается с уменьшением интервала обработки T), а по максимуму частотной зависимости функционала правдоподобия Δ(ω) /7/.

Δ ( ω ) = 1 1 − A ' ( ω ) * E n cos ( ω t n ) ¯ + B ' ( ω ) * E n sin ( ω t n ) ¯ E n 2 ¯                                                           ( 7 )

Функционал правдоподобия не зависит от интервала обработки T. Его ширина определяется отношением сигнал/шум. Следовательно, точность оценок квадратурных компонент широкополосного сигнала не меняется с уменьшением интервала T. Амплитуда и начальная фаза широкополосного сигнала находятся с помощью квадратурных компонент A′(ω=ω₀), B′(ω=ω₀) по выражениям

U ( ω = ω 0 ) = A ' ( ω 0 ) 2 + B ' ( ω 0 ) 2 ,   φ ( ω 0 ) = − a r c t g ( B ' ( ω 0 ) A ' ( ω 0 ) )                       ( 8 )

Обоснованием предлагаемого способа оценки параметров широкополосного сигнала является следующее: запишем выборку данных, содержащую широкополосный сигнал в виде:

E n = U 0 cos ( ω 0 t n + ϕ 0 ) + U ш , n                                                                                                           ( 9 )

где:

E_n - выборка измеряемых данных, полученная на интервале времени T с дискретностью Δt=τ_k.

U₀ - амплитуда сигнала.

ω₀, φ₀ - круговая частота и начальная фаза сигнала.

t_n - момент времени.

U_ш,n - аддитивный гаусовский шум со средним значением, равным нулю, дисперсией σ² и интервалом корреляции τ_k.

Составим функционал правдоподобия в соответствии с теорией оптимального приема /7, 8 /.

Δ 1 ( U , ω , ϕ ) = ∑ n = 1 N | E n − A ' ( ω ) cos ( ω t n ) − B ' ( ω ) sin ( ω t n ) | 2                                                           ( 10 )

где: N - количество отсчетов, содержащихся на интервале обработки T,

U, ω, φ - оценочные параметры широкополосного сигнала.

Минимизацию функционала можно провести методом наименьших квадратов по переменным A′(ω) и B′(ω) для заданной частоты ω.

В результате получаем систему уравнений правдоподобия

E n cos ( ω t n ) ¯ = A ' ( ω ) cos 2 ( ω t n ) ¯ − B ' ( ω ) sin ( ω t n ) cos ( ω t n ) ¯ E n sin ( ω t n ) ¯ = A ' ( ω ) sin ( ω t n ) cos ( ω t n ) ¯ − B ' ( ω ) sin 2 ( ω t n ) cos ( ω t n ) ¯                                                         ( 11 )

где черта сверху означает суммирование по индексу «n» на интервале обработки T.

Уравнения (11) определяют выражения для уточненных квадратурных компонент A′(ω), B′(ω) (6)

и выражения для поправочных коэффициентов (5) a(ω), b(ω), c(ω),

Подставляя полученные значения квадратурных компонент A′(ω) и B′(ω) в функционал правдоподобия (10), исключаем зависимость функционала от квадратурных компонент, а следовательно, от амплитуды U(ω) и начальной фазы φ(ω). После возведения в квадрат выражения (10), преобразования с учетом (11) и нормировки на первое слагаемое E n 2 ¯ получим значение функционала правдоподобия на заданной частоте ω в виде (12).

Δ 2 ( ω ) = 1 − A ' ( ω ) * E n cos ( ω t n ) ¯ + B ' ( ω ) * E n sin ( ω t n ) ¯ E n 2 ¯                                                 ( 12 )

Для удобства графического отображения обратим функционал Δ ( ω ) = 1 Δ 2 ( ω ) .

В результате получим функционал правдоподобия Δ(ω) (7).

Перебирая все частоты в заданном интервале, получим частотную зависимость функционала правдоподобия Δ(ω). Положение максимума функционала правдоподобия определяет оценку частоты ω=ω₀ и квадратурных компонент A′(ω=ω₀), B′(ω=ω₀). По квадратурным компонентам в соответствии с (8) оцениваются амплитуда и начальная фаза широкополосного сигнала U₀, φ₀. Согласно теории /7, 8/ значение функционала правдоподобия в максимуме определяет точность и достоверность полученных оценок параметров широкополосного сигнала. Шумовые максимумы функционала правдоподобия ограничены значением Δ(ω₀)≤20. Следовательно, чем больше значение функционала в максимуме, тем точнее и достовернее оценки параметров широкополосного сигнала.

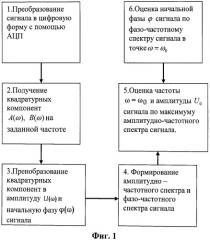
Эффективность предлагаемого способа поясняется таблицей и иллюстрациями.

Реализуемость данного способа оценки параметров широкополосного синусоидального сигнала иллюстрируется результатами модельных расчетов амплитуды U, начальной фазы φ и частоты ω сигнала в зависимости от длительности интервала обработки (Фиг.2). Модельные расчеты проведены в соответствии с алгоритмом действий прототипа по выражениям (2), (4) (оцениваемые параметры U₁, ω₁, φ₁) и в соответствии с алгоритмом действий предлагаемого способа по выражениям (5), (6), (7), (8) (оцениваемые параметры U₂, ω₂, φ₂). При модельных расчетах приняты следующие параметры: амплитуда сигнала U₀=1, фаза сигнала φ₀=50 градусов, частота ω₀=1.6 КГц, интервал дискретизации Δt=0.0625 мс, интервал обработки T меняется в пределах от 0.3 мс до 5.0 мс. Как видно из таблицы, предлагаемый способ оценивает параметры широкополосного сигнала гораздо точнее, чем способ спектрального оценивания (прототип). Погрешности оценки параметров предлагаемого способа не превышают долей градуса по фазе, двух Герц по частоте, 0.11% по амплитуде. Погрешности оценок спектрального анализа (прототип) значительно больше и они увеличиваются при уменьшении интервала обработки T.

На фиг.1 показана блок-схема устройства, с помощью которого реализуется прототип: способ оценки параметров сигнала с помощью спектрального анализа.

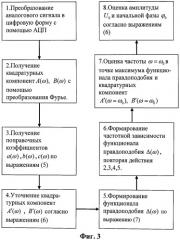
На фиг.3 представлена блок-схема устройства, реализующего предлагаемый способ оценки параметров широкополосных сигналов. Основным является оценка частоты по функционалу правдоподобия.

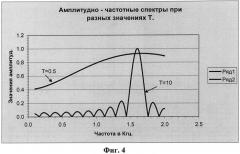
На фиг.4 показаны амплитудно-частотные спектры при интервалах обработки T=10 мс и при T=0.5 мс. С уменьшением интервала обработки ширина спектра увеличивается, а следовательно, и точности оценок параметров уменьшаются. Точность оценок параметров зависит от интервала обработки. Это основной недостаток оценок параметров широкополосных сигналов с помощью спектрального анализа.

На фиг.5 показана частотная зависимость функционала правдоподобия при интервале обработки T=0.5 мс. Максимум имеет вид дельта функции. Его ширина не зависит от длительности интервала обработки T, а следовательно, точности оценок параметров широкополосных сигналов высокие. Использование частотной зависимости функционала правдоподобия для оценок параметров широкополосных сигналов является основным в данной заявке.

Предлагаемый способ оценки параметров широкополосных сигналов осуществляют в устройстве, блок-схема которого показана на фиг.3.

1. Преобразуют входной сигнал в цифровую входную последовательность с интервалом дискретизации Δt=τ_k (τ_k - интервал корреляции шума) с помощью аналого-цифрового преобразователя (АЦП).

2. На заданной частоте со согласно выражениям (1) проводят синусное и косинусное преобразование Фурье и получают квадратурные компоненты A(ω), B(ω).

3. На заданной частоте со оценивают поправочные коэффициенты:

, b ( ω ) = sin 2 ( ω t n ) ¯ , c ( ω ) = cos ( ω t n ) sin ( ω t n ) ¯

4. На заданной частоте со рассчитывают уточненные квадратурные компоненты A′(ω), B′(ω) по выражениям

5. Подставляя полученные значения квадратурных компонент A′(ω), B′(ω) в функционал правдоподобия Δ(ω) (5), получают его значение на частотен.

Δ ( ω ) = 1 − A ' ( ω ) * E n cos ( ω t n ) ¯ + B ' ( ω ) * E n sin ( ω t n ) ¯ E n 2 ¯ ,                                                           ( 5 )

6. Перебирая частоты в заданном диапазоне и каждый раз выполняя действия 1-5, формируют частотную зависимость функционала правдоподобия Δ(ω).

7. В точке максимума частотной зависимости функционала правдоподобия Δ(ω=ω₀) оценивают частоту ω=ω₀ и квадратурные компоненты сигнала A′(ω₀), B′(ω₀).

8. По квадратурным компонентам определяют амплитуду и фазу сигнала по выражениям (6).

U ( ω 0 ) = A ' ( ω 0 ) 2 + B ' ( ω 0 ) 2 = U 0 ,   φ ( ω 0 ) = a r c t g ( B ' ( ω 0 ) A ' ( ω 0 ) ) = ϕ 0                                     ( 6 )

В результате параметры сигнала оцениваются на любом интервале времени T. Ширина функционала правдоподобия зависит от отношения сигнал/шум и не зависит от длительности интервала измерения.

Источники, принятые во внимание

1. Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов по специальности «Радиотехника». - 2-е изд.- М.: Высшая шк., 1988-448 с.,6 ил.

2. Сергиенко А.Б. Цифровая обработка сигналов: Учебное пособие для вузов по специальности «Информатика и вычислительная техника». - СПб.: Питер, 2005. - 604 с.: ил.

3. В.Г.Радзиевский, П.А.Трифонов. Обработка сверхширокоподобных сигналов и помех. - М.: «Радиотехника», 2009. - 288 с.

4. Марпл.-мл. С.Л. Цифровой спектральный анализ и его применения: Пер. с англ. - М.: Мир, 1990. - 584 с.

5. А.С. №541123. Толстых B.C. Способ измерения частоты. М. :ЦНИИПИ, 1977, - 2 с.

6. А.С. №1798717. Минц М.Я. и др. Способ измерения частоты синусоидальных сигналов. -М. :ВНИИПИ, 1987, - 9 с.

7. А.И.Перов. Статистическая теория радиотехнических систем. - М.: Радиотехника, 2003, 400 с., ил.

8. В.А.Пахотин, В.А.Бессонов, С.В.Молостова, К.В.Власова. - Калининград: Изд.-во РГУ им. И.Канта, 2008. - 189 с.

1. Способ определения параметров широкополосного сигнала, включающий преобразование сигнала в цифровую входную последовательность с помощью аналого-цифрового преобразователя, определение по формулам преобразования Фурье на заданной частоте ω двух квадратурных компонент , , где черта сверху означает суммирование по индексу n, отличающийся тем, что дополнительно на заданной частоте ω определяют поправочные коэффициенты a(ω), b(ω), c(ω), с помощью которых уточняют квадратурные компоненты A′(ω) и B′(ω) , ,по которым вычисляют значение функционала правдоподобия Δ(ω) ,методом перебора частот в заданном диапазоне определяют частотную зависимость функционала правдоподобия Δ(ω), оценивают в точке максимума частотной зависимости функционала правдоподобия частоту ω=ω₀ и квадратурные компоненты A′(ω₀) и B′(ω₀), по которым оценивают амплитуду U₀ и начальную фазу φ₀ сигнала согласно выражениям , ,интервал дискретизации входной последовательности Δt выбирают исходя из условия Δt=τ_к, где τ_к - интервал корреляции шума.