Способ оценки гамма-процентного ресурса изделия по результатам неразрушающего контроля с использованием тест-образцов со скрытыми дефектами

Способ оценки гамма-процентного ресурса изделия по результатам неразрушающего контроля с использованием тест-образцов со скрытыми дефектами

Иллюстрации

Показать все

Реферат

Изобретение относится к способам испытаний, в частности, для оценки показателей долговечности изделия, точнее гамма-процентного ресурса изделия. Изобретение может применяться в транспорте, атомной и традиционной энергетике, авиации, судостроении, нефтехимии, нефте-, газо- и продуктопроводах, сельскохозяйственных машинах и других областях техники и машиностроения.

Гамма-процентный ресурс - это ресурс, в течение которого изделие не достигнет предельного состояния с вероятностью γ, выраженной в процентах (ГОСТ53480-2009 Надежность в технике. Термины и определения).

В качестве прототипа выбран способ определения качестве изделий, раскрытый в патенте RU 2243586 C1 (опубликован 27.12.2004). Данный способ позволяет определять остаточную дефектность. Однако данный способ не позволяет определять параметры надежности изделия, в частности гамма-процентный ресурс, и их изменение в ходе эксплуатации изделия.

Предельные состояния изделий (механических изделий), как правило, связаны с дефектами металла (или другого конструкционного материала), из которого изготовлено изделие. В соответствие с существующими правилами и нормами в технике устанавливаются допустимые размеры несплошностей, превышение которых запрещено. Такие несплошности называются дефектами. Дефекты, в случае их обнаружения методами неразрушающего контроля, устраняются ремонтом. В процессе эксплуатации несплошности и дефекты материала изделия могут развиваться и увеличиваться в размере, приводя к окончательной поломке или разрушению изделия. Для своевременного выявления опасных несплошностей применяют неразрушающий контроль.

Гамма-процентный ресурс изделия настоящим изобретением предлагается определять по результатам неразрушающего контроля (далее НК) несплошностей, неоднородностей и других дефектов материала изделия или группы изделий (деталей, элементов конструкций и т.п.), в том числе ультразвукового, вихретокового, радиографического и других методов НК.

Считается, что после проведения неразрушающего контроля и ремонта по его результатам всех выявленных дефектов в изделии отсутствуют дефекты. При этом считается, что надежность и безопасность изделия в эксплуатации обеспечена (см., например, нормативные документы в области атомной энергетики: «Правила устройства и безопасной эксплуатации оборудования и трубопроводов атомных энергетических установок» ПНАЭГ-7-008-89, «Оборудование и трубопроводы атомных энергетических установок. Сварные соединения и наплавки. Правила контроля» ПНАЭГ-7-010-89, Госатомнадзор России, Энергоатомиздат, 1991 г.).

На самом деле в настоящее время в технике практически отсутствуют методы и средства неразрушающего контроля, гарантированно, со 100%-ной достоверностью выявляющие все дефекты. Поэтому всегда имеется определенная вероятность пропуска дефекта, в том числе и дефекта, представляющего опасность (то есть развитие которого во время эксплуатации приведет к повреждению изделия или его разрушению). Известно (например, Аркадов Г.В., Гетман А.Ф., Родионов А.Н. Надежность оборудования и трубопроводов АЭС и оптимизация их жизненного цикла, М., Энергоатомиздат, 2010; Гурвич А.К. «Надежность дефектоскопического контроля как надежность комплекса «Дефектоскоп - оператор - среда», Дефектоскопия, 1992 г., №3, с.5-13), что практически во всех случаях НК имеется существенная вероятность пропуска дефекта больших размеров, существенно превышающих допустимые размеры. На практике оказывается, что практически всегда после НК и устранения выявленных дефектов в изделии еще остаются дефекты. Именно эти оставшиеся дефекты в конечном итоге и определяют надежность и долговечность изделия.

Существующие методы оценки гамма-процентного ресурса изделия основаны на формально-математических подходах, в которых не учитываются реальные оставшиеся в изделии дефекты. Например, в рамках существующих теорий надежности фактический уровень гамма-процентного ресурса изделия определяют по результатам математической обработки так называемого потока отказов однотипных изделий, находящихся в эксплуатации (Острейковский В.А. «Эксплуатация атомных станций», Москва, Энергоатомиздат, 1999 г., раздел 3.5: «Методы анализа несплошностей оборудования АЭС»). Недостаток таких подходов состоит в том, что находящиеся в эксплуатации изделия должны повредиться или разрушиться прежде чем можно будет оценить их фактический уровень надежности и безопасность.

Технический результат, на достижение которого направлено данное изобретение, заключается в том, что оно позволяет произвести оценку реальной дефектности изделия после контроля и ремонта выявленных дефектов и определить фактический уровень гамма-процентного ресурса изделия до того, как оно разрушится или повредится в эксплуатации.

Пример осуществления изобретения иллюстрируется следующими графическими материалами.

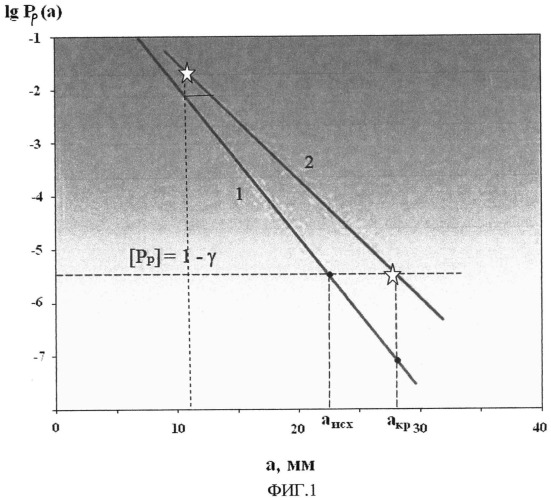
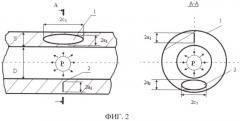
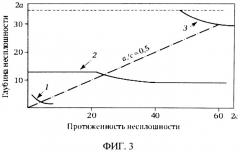
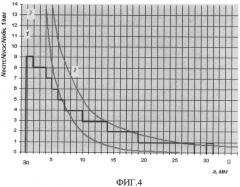
На фиг.1 представлены кривые остаточной дефектности до начала эксплуатации и в конце эксплуатации. На фиг.2 изображена схематизация дефекта в трубопроводе эллипсом с полуосями a и c. На фиг.3 показана совокупность дефектов критических и допустимых размеров. На фиг.4 показана гистограмма выявленных в изделии дефектов, кривые исходной и остаточной дефектности. На фиг.5 показан график для определения вероятности обнаружения дефектов.

Технический результат достигается тем, что способ определения гамма-процентного ресурса изделия включает определение дефектности изделия методом неразрушающего контроля, при этом изготавливают тест-образец, предназначенный для определения характеристик неразрушающего контроля несплошностей в материале изделия, осуществляют контроль этого тест-образца методом неразрушающего контроля и контроль изделия, который производится тем же методом, что и контроль тест-образца, при этом тест-образец изготавливают в форме изделия или его наиболее ответственной части из того же материала и по той же технологии, что и изделие с расположенными случайным образом дефектами с различными характеристическими размерами χ, определяют для конкретного изделия или группы m однотипных изделий критические размеры χ_кр дефектов в режиме эксплуатации и допустимые в эксплуатации размеры [χ]_д.э. дефектов, результаты контроля изделия представляют в виде гистограммы в координатах (N_обн, χ), где N_обн - число обнаруженных при контроле дефектов, χ - характеристический размер дефекта, причем при контроле m однотипных изделий результаты контроля суммируют и представляют в виде одной гистограммы, определяют вероятность обнаружения дефектов P_вод на упомянутом тест-образце, определяют исходную дефектность N_исх=f(χ), определяют остаточную дефектность N_ост=φ(χ) как разность N_исх и N_обн, остаточную дефектность разделяют на достоверную часть χ≤χ_д и вероятностную часть χ>χ_д, где χ - характеристический размер дефекта, χ_д - размер дефектов на границе между достоверной и вероятностной частями, определяемый из

∫ χ д χ м а к с ϕ ( χ ) d χ = 1 ,

где χ_макс - максимально возможные размеры дефектов в данном изделии;

полученная вероятностная часть остаточной дефектности принимается за начальную кривую остаточной дефектности, которая сдвигается вправо на графике в координатах (lgP_р; χ), где P_р - вероятность разрушения, за счет развития дефектов в эксплуатации, при этом величину развития определяют расчетным путем в зависимости от механизма и условий эксплуатации; полученную новую кривую принимают за конечную кривую остаточной дефектности и по ней определяют значения гамма-процентного ресурса по критериям либо появления недопустимого в эксплуатации дефекта, либо по критерию разрушения, при этом в первом случае используют уравнение

γ_t([χ]_д.э.)=[1-P_p(χ_д.э.)]×100%,

а во втором случае уравнение

γ_t(χ_кр)=[1-P_p(χ_кр)]×100%.

Отличительной чертой данного способа является то, что для определения гамма-процентного ресурса используют тест-образец, фактически идентичный изделию.

По вероятностной части конечной остаточной дефектности определяют вероятность гамма-процентного ресурса изделия γ_t как вероятность отсутствия в изделии несплошности недопустимого размера по формуле:

γ t ( [ χ ] д . э . ) = [ 1 − 1 m ∫ [ χ ] д . э . χ м а к с ϕ ( χ ) d χ ]

а гамма-процентный ресурс изделия по критерию разрушения можно определить как вероятность отсутствия в изделии несплошности, по размерам равной или большей χ_кр, по формуле:

γ t ( χ к р ) = [ 1 − 1 m ∫ χ к р χ м а к с ϕ ( χ ) d χ ]

Для того чтобы гамма-процентный ресурс выразить в процентах, надо величину γ_t([χ]_д.э.) или γ_t(χ_кр) умножить на 100%.

Как правило, в качестве характеристического размера χ дефекта выбирается линейный размер a дефекта, или комбинация линейных размеров дефекта, или площадь дефекта, или объем дефекта.

В одном из вариантов аппроксимируют гистограмму (N_обн, χ) уравнением

N_обн(χ)=A₁χ^-n ₁{1-(1-η)exp[-α(χ-χ₀)]-η} или

N_обн(χ)=A₂exp(-n₂χ){1-(1-η)exp[-α(χ-χ₀)]-η},

где A₁, А₂, n₁, n₂, η - постоянные, которые определяют из условия максимального приближения уравнения N_обн(χ) к результатам контроля, представленным в виде гистограммы, а α определяют с использованием тест-образца,

χ₀ - минимально доступный для выявления размер дефекта,

исходную дефектность N_исх определяют по формуле:

N_исх=Аχ^-n

а вероятность обнаружения дефекта P_вод аппроксимируют по результатам контроля тест-образца формулой:

P_вод=1-(1-η)exp[-α(χ-χ₀)]-η.

В частном случае в качестве характеристического размера χ принимают малую полуось a эллипса, которым схематизируют дефект, при этом соотношение а/с принимают постоянным для всех а, определяемым из условия максимальной скорости развития дефекта в эксплуатационных условиях.

При этом минимально доступный для выявления размер дефекта χ₀ определяют при настройке дефектоскопа, применяемого при контроле изделия, или как минимальный размер дефекта, который был выявлен при контроле.

Для упрощения вычислений постоянную η можно принимать равной 0.

Зависимость (N_исх, χ) апроксимируют уравнением типа N_исх=А_χexp(-n_χχ), или N_исх=A_aехр(-n_a a), или N_исх=A_a,cexp[-n_a,c(a ²/c)], или N_исх=A_Fexp(-nF), или N и с х = A χ χ − n χ , или N и с х = A a a − n a , или N и с х = A a , c ( a 2 / c ) − n a , c , или N и с х = A F F − n F ,

где а, с - линейные размеры дефекта,

F - площадь дефекта,

n, A - коэффициенты, выбираемые из условия максимального приближения аналитической кривой к экспериментальным данным.

Способ может применяться для конкретного изделия или группы однотипных изделий, гамма-процентный ресурс которых надо определить, с применением известного метода НК при проведении контроля оператором известной квалификации с последующим ремонтом выявленных дефектов.

Методами механики разрушения определяют критические размеры дефектов в режиме эксплуатации для данного изделия χ_кр и предельно допустимые в эксплуатации дефекты [χ]_д.э. (нормы дефектов изделия), определяемые по действующим нормативным документам и/или ТУ на изготовление (например, для атомной техники - по нормативной методике М-02-91). χ - характеристический размер дефекта, например, выбирается линейный размер дефекта, или комбинация линейных размеров дефекта, или площадь дефекта, или объем дефекта.

Фиг.1 иллюстрирует тот факт, что определенная указанным выше способом кривая остаточной дефектности принимается за исходную (то есть на момент оценки, например, до начала эксплуатации) остаточной дефектностью (кривая 1 на фиг.1), которая за время эксплуатации t_э (за счет того, что дефекты подрастут) сдвинется вправо (фиг.1, кривая 2). Новую кривую остаточной дефектности принимают за конечную кривую остаточной дефектности.

Совокупность дефектов критических размеров (кривая 3), допустимых в эксплуатации размеров (кривая 2), а также допустимые размеры несплошностей при изготовлении (кривая 1) изображены на фиг.3.

Проводят неразрушающий контроль изделия (НК) выбранным методом (ультразвуковым, вихретоковым, радиографическим и другими методами НК), техническими средствами контроля и операторами определенной квалификации и затем устраняют в нем обнаруженные дефекты (ремонтом).

Результаты контроля представляют в виде гистограммы в координатах «характеристический размер дефекта χ - количество выявленных дефектов данного размера N_{обн изд}».

Далее определяют исходную дефектность N_исх=f(χ) и остаточную дефектность N_ост=φ(χ) по уравнению N_исх(χ)=N_обн(χ)/P_вод(χ) как разность N_исх и N_обн.

Указанные зависимости можно определять следующим способом. Результаты НК представляют в виде аналитических выражений. Структура уравнения, которое может описать результаты НК, представленные на гистограмме, фиг.4, следующая:

N_обн(χ)=N_исх(χ)P_вод(χ)

где N_обн - число обнаруженных при контроле дефектов на единицу характеристического размера. Если в качестве характеристического размера выбрана малая полуось эллипса, которым схематизируют дефект, то размерность N_обн - мм^-1;

N_исх - функция исходной (до НК и ремонта) дефектности с той же размерностью, что и N_обн;

P_вод - вероятность обнаружения дефекта данного размера χ.

Вид функции N_исх определяется исходя из условия наибольшей простоты выражения, минимального числа констант и соответствия физически обусловленной зависимости N_исх от χ.

В первом приближении могут быть использованы следующие уравнения:

N_исх=Aχ^-n,

P_вод=1-(1-η)exp[-α(χ-χ₀)]-η,

N_обн(χ)=Aχ^-n{1-(1-η)exp[-α(χ-χ₀)]-η},

где A, n, α, η, χ₀ - постоянные.

Определяют численные значения постоянных A, n, α, η из условия максимального приближения уравнения N_обн(χ) к результатам НК, представленным в виде гистограммы. При этом α и η определили ранее на тест-образце.

При этом χ₀ - минимально доступный для выявления размер дефекта - определяют при настройке дефектоскопа, применяемого при контроле изделия, или как минимальный размер дефекта, который был выявлен при контроле; η в первом приближении можно принять равной 0. В результате остается две неизвестных, что существенно облегчает задачу их определения.

Определить постоянные A и n можно либо решая систему двух уравнений относительно A и n, которые получают, если взять две точки на гистограмме, либо их определяют с использованием метода наименьших квадратов.

Остаточную дефектность N_ост определяют как разность N_исх и N_обн:

N_ост(χ)=N_исх(χ)-N_обн(χ).

При этом число оставшихся после НК и ремонта дефектов в изделии определяют в трех диапазонах: остаточную дефектность N о с т ,   к р Σ в области дефектов, важных для безопасности, определяют в виде числа дефектов в изделии, размеры которых равны или больше критических размеров χ_кр в режиме эксплуатации изделия: N о с т , к р Σ = 1 m ∫ χ к р χ п р е д N о с т ( χ ) d χ ; при N о с т ,   к р Σ < 1 имеется вероятность неразрушения изделия; при N о с т ,   к р Σ ≥ 1 изделие не имеет запаса безопасности и не может быть допущено к эксплуатации;

остаточную дефектность N о с т ,   д . э . Σ в области дефектов, важных для надежности, определяют в виде числа дефектов, размеры которых превышают размеры дефектов [χ]_д.э., предельно допустимых в эксплуатации изделия:

N о с т , д . э . Σ = 1 m ∫ χ д . э . χ п р е д N о с т ( χ ) d χ ; при N о с т ,   д . э . Σ ≥ 1 изделие не имеет запаса надежности;

где m - число однотипных изделий.

При построении гистограммы горизонтальная ось χ должна включать критический размер дефекта, даже если в результате контроля все выявленные дефекты не достигали критических размеров.

В случае контроля нескольких однотипных изделий все результаты контроля суммируют и представляют в виде одной гистограммы. Чем большее количество изделий было проконтролировано, тем достовернее получаемый окончательный результат.

Кривую вероятности выявления дефектов от размеров дефектов "a" и "с" (любой дефект в материале консервативно можно описать эллипсом с полуосями a и с) можно аппроксимировать наиболее близко описывающим экспериментальные результаты контроля уравнением, например

P_вод=1-(1-η)exp[-α_НК(a-a ₀)(c-c₀)]-η, или

P в о д = 1 − ( 1 − η ) exp [ − α Н К ( a − a 0 ) a c ] − η , или

P_вод=1-(1-η)exp[-α_НК(χ-χ₀)]-η

где α_НК - коэффициент достоверности НК, характеризует увеличение выявляемости дефектов в зависимости от его размера;

η - постоянная, характеризующая предельную выявляемость контроля данным методом при сколь угодно большом размере дефекта; если размеры детали небольшие, то данной величиной можно пренебречь, введя соответствующую корректировку величины α_НК;

χ -характеристический размер дефекта, например его площадь;

χ₀ - минимальный характеристический размер дефекта;

а₀, c₀ - минимальные размеры дефектов, доступные для выявления НК.

Далее проводят контроль изделия, а результаты контроля представляют в виде гистограммы в координатах «характеристический размер дефекта χ - количество выявленных дефектов данного размера N_{обн изд}».

Исходную дефектность N_исх определяют как отношение N_{обн изд}/P_вод(χ); полученную гистограмму апроксимируют уравнением типа N_исх=A_χexp(-n_χχ), или N и с х = A χ χ − n χ , или N и с х = A a a − n a , или N и с х = A a , c ( a 2 / c ) − n a , c , или N и с х = A F F − n F , или

N и с х = A a a − n a   ρ ( c ) , или N и с х = A a , c a − n 1 2 π D exp [ ( c − c ¯ ) 2 2 D 2 ( c ) ]

где а, с - линейные размеры дефекта,

ρc - функция распределения величины с, например, нормальный закон распределения,

F - площадь дефекта,

n, A, D, c ¯ - коэффициенты, выбираемые из условия максимального приближения аналитической кривой к экспериментальным данным, при этом c ¯ - среднее значение с, а D - дисперсия.

В качестве характеристического размера можно принять малую полуось a эллипса, которым схематизируют дефект, при этом соотношение а/с принимают постоянным для всех а исходя из условия максимальной скорости роста дефекта в условиях эксплуатации; при этом

N и с х = ∫ 0 c м а к с ϕ ( a , c ) d c = f ( a ) , например, в случае однородного поля напряжений a/с=2 и нормального закона для распределения с со средним значением с=2a и дисперсией D=a/2 получаем

N и с х = ∫ 0 c м а к с A a − n 1 2 π D exp [ − ( c − c ¯ ) 2 2 D 2 ( c ) ] d c = = A a − n ∫ 0 c м а к с 2 a π exp [ − ( c − 2 a ) 2 / 0,5 a 2 ] d c = A a − n

Остаточную дефектность получают как разность между N_исх и N_{обн изд}. При этом N_{обн изд} определяют из аналитического выражения N_исх·P_вод(χ), т.e. остаточную дефектность N_ост можно представить в виде уравнения

N_ост=N_исх(1-P_вод).

Далее остаточную дефектность разделяют на достоверную часть χ≤χ_д, в которой дефекты с размерами χ≤χ_д существуют достоверно, и вероятностную часть χ>χ_д, в которой дефекты с размерами χ>χ_д могут быть, а могут и не быть.

Границу между достоверной и вероятностной частями остаточной дефектности определяют из условия:

∫ χ д χ м а к с ϕ ( χ ) d χ = 1 ,

где χ_макс - максимально возможные размеры дефектов в данном изделии.

Полученная таким образом вероятностная часть остаточной дефектности будет начальной кривой остаточной дефектности. За время эксплуатации t_э (за счет того, что дефекты подрастут) эта кривая сдвинется вправо (кривая 2 на фиг.1). Величины сдвигов вправо можно определить по известным формулам в зависимости от исходного размера дефекта, например по нормативному документу в атомной энергетике РД ЭО-0330 или упоминавшейся выше монографии Аркадова Г.В., Гетмана А.Ф. и Родионова А.Н. Полученная новая кривая остаточной дефектности будет конечной остаточной дефектностью.

По вероятностной части конечной остаточной дефектности определяют вероятность гамма-процентного ресурса изделия γ_t как вероятность отсутствия в изделии несплошности недопустимого размера по формуле:

γ t ( [ χ ] д . э . ) = [ 1 − 1 m ∫ [ χ ] д . э . χ м а к с ϕ ( χ ) d χ ] ,

а гамма-процентный ресурс изделия по критерию разрушения можно определить как вероятность отсутствия в изделии несплошности, по размерам равной или большей χ_кр, по формуле:

γ t ( χ к р ) = [ 1 − 1 m ∫ χ к р χ м а к с ϕ ( χ ) d χ ] .

Для того чтобы гамма-процентный ресурс выразить в процентах, надо величину γ_t([χ]_д.э.) или γ_t(χ_кр) умножить на 100%.

Изобретение иллюстрируется следующим примером.

Необходимо определить гамма-процентный ресурс на конец проектного срока эксплуатации трубопровода внутренним диаметром D=800 мм, толщиной стенки S=34 мм из перлитной стали. Критические размеры дефектов в поперечных сварных швах представлены на фиг.3 (кривая 3). Допустимые в эксплуатации дефекты определили с использованием уравнений механики разрушения и коэффициентов запаса прочности (кривая 2 на фиг.3). Нормы дефектов при изготовлении представлены на фиг.3 кривой 1.

В результате НК штатным методом и средствами до начала эксплуатации (после монтажа) было обнаружено 71 несплошность.

Все выявленные несплошности (дефекты) представлены в виде гистограммы на фиг.4.

При этом в качестве характеристического размера дефекта выбрана ширина дефекта в направлении толщины стенки, а точнее - малая полуось эллипса, которыми схематизировали все выявленные дефекты.

При соотношении a/с≈0,5 критическому размеру дефекта соответствует a _кр=28 мм, [a]_д.э.=11 мм, [a]_изг.=1,15 мм (фиг.2).

Несмотря на то, что максимальный размер выявленного дефекта составил a _макс=13 мм, ось абсцисс содержит критический размер a=28 мм.

Уравнение, описывающее число выявленных дефектов N_обн в зависимости от размеров a:

N_обн=Aa ^-n[1-exp[-α(a-a ₀)]].

По результатам контроля минимальный выявленный дефект имел a=0,6 мм, то есть a ₀=0,6 мм.

Вероятность обнаружения дефектов определяют с использованием тест-образца и аппроксимируют выражением P_вод=1-exp[-α(1-0,6)].

Для определения постоянных А, n решают систему из двух уравнений относительно этих постоянных:

1-е уравнение получают для точки с координатами (a=1 мм, N_обн=20) по фиг.4:

20=A·1^-n[1-exp[-α(1-0,6)]];

2-е уравнение получают для точки с координатами (a=5 мм, N_обн=4) по фиг.4:

4=A·5^-n[1-exp[-α(5-0,6)]];

3-е уравнение получают для точки с координатами (a=13 мм, N_обн=0,66) по фиг.4 и его можно использовать для уточнения коэффициентов A и n:

0,66=A·13^-n[1-exp[-α(13-0,6)]].

Для 3-го уравнения N_обн=0,66 получено как осреднение числа выявленных дефектов в интервале от 11 до 13 мм, что составило 2/3, где 2 - число выявленных дефектов, 3 - число интервалов.

Окончательно система уравнений имеет вид:

20=A·[1-exp(-0,4α)]

4=A·5^-n[1-exp(-4,4α)]

0,66=A·13^-n[1-exp(-12,4α)]

Решение системы уравнений относительно A и n дало следующие результаты:

А=1000 мм, n=2,56. Коэффициент α=0,05 мм^-1 определен ранее экспериментально из тест-образца.

Подставляя постоянные A, n, а в соответствующие уравнения, получают уравнение исходной дефектности:

N_исх=1000a ^-2,56;

уравнение вероятностей обнаружения дефекта:

P_вод=1-exp[-0,05(a-0,6)];

уравнение остаточной дефектности

N_ост(χ)=N_исх(χ)-N_обн(χ).

Полученные уравнения представлены на фиг.4 и фиг.5.

Решают уравнения

γ t ( [ χ ] д . э . ) = [ 1 − 1 m ∫ [ χ ] д . э . χ м а к с ϕ ( χ ) d χ ]

γ t ( χ к р ) = [ 1 − 1 m ∫ χ к р χ м а к с ϕ ( χ ) d χ ]

где φ(χ)=φ(χ)=N_ост(a)=N_исх(a)-N_обн(a), а m=1

При этом a_макс=S, где S - толщина стенки трубопровода. Результаты решения представлены на фиг.1 в виде кривой 1. Допустимые в эксплуатации и критические дефекты отмечены соответственно [a] и a _кр.

Результаты расчета в координатах {lg(1-χ); a} наносим на график (кривая 1 на фиг.1). Полученная кривая 1 является начальной кривой вероятностной части остаточной дефектности.

Во время эксплуатации дефекты будут расти. Механизм роста может быть различным в зависимости от условий эксплуатации. В нашем случае превалирует рост дефектов под действием циклических нагрузок. В этом случае используем уравнение типа:

d a d N = C ⋅ ( Δ K 1 1 − R ) m ,

в котором

C и m - постоянные, зависящие от материала и условий эксплуатации;

R - коэффициент асимметрии цикла, для цилиндра давления равен 0;

ΔK₁ - размах коэффициента интенсивности напряжений.

Коэффициент интенсивности напряжений при неоднородном распределении напряжений в районе трещины определяют по уравнению:

K 1 = Y * σ к р * ( a / 1000 ) 0,5 ,

где

Y=(2-0,82(a/c))/[1-(0,89-0,57(a/c)^0,5)³(a/c)^l,5]^3,25,

σ_кр=0,61 σ^A+0,39σ^B+[0,11(a/с)-0,28(a/s)(1-(a/c)^0,5)](σ^A-σ^B), (5)

σ^A - напряжение в вершине трещины;

σ^B - напряжение на поверхности детали в корне трещины.

Для частного случая Y = 1.12 π .

Интегрируя приведенное выше выражение, его можно представить в виде:

N = ∫ a 0 a k 1 / C ⋅ ( Δ K 1 1 − R ) m d a

Подставляя в выражение предыдущие выражения и решая его относительно конечного размера трещины a _к, можно определить подрост трещины Δa _N под воздействием N циклов нагружения.

Определяя указанным способом подрост дефектов для верхней, средней и нижней частей начальной кривой остаточной дефектности для числа циклов нагружения на конец проектного срока эксплуатации, получим конечную кривую остаточной дефектности (кривая 2 на фиг.1).

По конечной кривой остаточной дефектности определяем гамма-процентный ресурс трубопровода по критериям обнаружения недопустимого дефекта и по критерию разрушения (разрыва), соответственно

γ_t([χ]_д.э.)=1-P_р(a _д.э.) и γ_t(χ_кр)=1-P_р(a _кр),

или для пр