Способ сложносоставной оптимальной фильтрации для обнаружения слабых сигналов

Способ сложносоставной оптимальной фильтрации для обнаружения слабых сигналов

Иллюстрации

Показать все

Реферат

Область техники

Заявленый способ обработки информации на основе метода сложносоставной оптимальной фильтрации слабого сигнала космического радиолокационного комплекса (КРК) относится к области радиотехники.

Уровень техники

Методы оптимальной фильтрации давно используются в радиолокации для селекции движущихся целей по скорости (СДЦ) на фоне помех [1]. Скорость V цели создаёт доплеровский сдвиг f_Д= 2·V/λ, где λ- длина волны несущей частоты, в моностатической (однопозиционной) радиолокации и f_Д= V/λ в бистатической (двухпозиционной) радиолокации. В качестве прототипа выбрана система СДЦ, описанная в [2].

Известно, что в космических радиолиниях: радиовещания (спутники серии "Экспресс"), радиосвязи ("Молния", "Меридиан" и др.) радионавигации (ГЛОНАСС, GPS), радиолокации ("Днепр-3У", "Дарьял", "Волга" и др.), комплексах дистационного зондирования ионосферы [3] существуют сильные искажения частоты, обусловленные изменением электронной плотности ионосферы в пространстве и времени. Эти искажения частоты изменяют информационный сигнал, генерированный передатчиком или обусловленный рассеянием электромагнитной волны движущейся радиолокационной цели. Для компенсации этих искажений применяют различные виды частотных корректоров.

В качестве первого аналога способа сложносоставной оптимальной фильтрации для компенсации искажения доплеровского сигнала из-за влияния ионосферы выбрана цифровая система вычисления линейной по времени добавки к доплеровской частоте передатчика спутника по результам измерения полного изменения частоты спутникового передатчика в ГЛОНАСС [4].

Принимаемые сигналы, отраженные от космических целей (в радиолокации) или излученные со спутников (в радиосвязи и радиовещании), имеют малый уровень мощности на Земле (менее -160 дБВт), который на 20 дБ÷60 дБ ниже уровня входных шумов приёмника. Приём таких слабых сигналов обычно осуществляется способом оптимальной фильтрации, в котором опорный (модельный) наземный сигнал в оптимальном приёмнике известен. Однако простые методы оптимальной (согласованной) фильтрации по целому ряду причин не обеспечивают высокую степень подавления помехи, например по указанной выше причине искажения сигнала в ионосфере, высокого уровня нестационарного и не гауссового шума спутникового передатчика, не определёнными движениями спутника и космической цели и многими другими причинами естественного и исскуственного происхождения.

Однако существуют сложные оптимальные фильтры, состоящие из последовательно соединённого согласованного фильтра с когерентным накоплением сигнала и фильтра с некогерентным накоплением.

В качестве второго аналога заявленного способа применяется принцип фильтрации с помощью сложносоставного фильтра, используемого в ГЛОНАСС или GPS [4].

Сущность изобретения

Введение

Точное знание частоты доплеровского сигнала спутникового передатчика в системах космической радиосвязи необходимо для коррекции сигнальных кодов, которые однако чувствительны к искажениям фазы и частоты сигнала. В системах космической радиолокации знание доплеровской частоты цели позволяет осуществить устойчивое сопровождение цели по скорости и, кроме того, осуществить передачу достоверной информации о скорости цели в систему ПРО или СПРН. В системах космической навигации точное знание доплеровской частоты спутникового передатчика реализует высокоточное вычисление местоположения потребителя информации ГЛОНАСС или GPS.

Поскольку сигнал в виде электромагнитной волны от спутника или от космической цели движется часть времени в ионосфере, представляющей собой ионизированную и намагниченную плазму, которая не стабильна и возмущается солнечным излучением, то электромагнитная волна в этой среде диспергирует и сдвигается во времени, при этом меняется частота и фаза волны. Это приводит к искажению информации. В результате теоретических и экспериментальных исследований по дистанционному зондированию ионосферы со спутников и с Земли сигналами различной формы и, в частности, ЛЧМ-сигналом спутникового передатчика обнаружено многократное по времени дисперсиооное расплытие импульсов зондирующего ЛЧМ-сигнала, а также задержка по времени в несколько микросекунд при периоде СВЧ-несущей частоты 0,1 нс ÷1 нс [5]. Существуют различные способы учесть это искажение сигнала. Один из этих способов предложен в заявленном изобретении.

С целью выделения слабого сигнала на фоне шума применяют оптимальные свёрточные фильтры. В простейшем случаеАЧХ фильтра является комплексно-сопряжённой функцией обнаруживаемого сигнала (кода). Такие фильтры с базой ЛЧМ-сигнала порядка 30 дБ теоретически обеспечивают подавление помехи на 30÷40 дБ. Используют и более сложное помехозащищающее кодирование, например, элементные бинарные коды Баркера с базой кода порядка 60 дБ или многоэлементные коды Костаса с базой порядка 100 дБ, которые обеспечивают подавление помехи до 100 дБ и выше. Однако выходной сигнал такого фильтра (отклик оптимального фильтра) в виде корреляционной функции принимаемого зашумленного кода и модельного кода чувствителен к заведомо неизвестному доплеровскому сдвигу частоты несущего сигнала, который к тому же ещё искажён влиянием ионосферы. Так, например, искажение параметров излученного сигнала по частоте (или неопределённость модельного сигнала) на 1% уменьшает степень подавления на 10 дБ, на 2 % уменьшает степень подавления на 20 дБ и т.д., что не приемлемо в реальных системах космической радиосвязи и радиолокации. Поэтому требуется точное знание доплеровского сдвига частоты и искажения этого доплеровского сдвига, которые используется для коррекции кодов в декодере-дискриминаторе в приёмнике на Земле. Существуют и нечувствительные к доплеровскому сдвигу методы помехозащищающего кодирования, например комплиментарные коды (дуально-параллельные), но они имеют свои недостатки, которые не относятся к предмету данной эаявки на изобретение.

Существуют нелинейные оптимальные фильтры, менее чувствительные к вариации параметров фильтра (или искажению модельного сигнала), однако они имеют значительно меньшую степень подавления помехи и не универсальны, то есть их расчётные параметры (по принятому критерию оптимальности) справедливы только для конкретных сигналов-кодов в рассчётном узком диапазоне амплитуд, фаз и частот, что не всегда можно обеспечить на практике.

В системах оптимальной фильтрации космических радиолиний широко используются сложные оптимальные фильтры, в которых используется кодированный сигнал, например псевдослучайной последовательности (ПСП) двоичных импульсов как в системе ГЛОНАСС [4].

Сначала этот сигнальный код детектируется в форме корреляционного отклика в согласованном корреляционном фильтре с когерентным накоплением типа свёртки с подавлением помехи на 35 дБ. Затем многие корреляционные отклики от многих пакетов импульсов ПСП (512 двоичных импульсов в пакете для ГЛОНАСС или 1028 - для GPS) фильтруются путём некогерентного накопления в аддитивном сумматоре откликов с дополнительным подавление ещё на 10 дБ, в сумме подавление помехи равно на 45 дБ и более.

Известны [6] нелинейные детекторы с ограничением сигнала, в которых шум больший, чем сигнал ослабляется, а слабый сигнал наоборот усиливается. Важным свойством этих детекторов является возрастание в 2 раза отношения сигнал/шум (СШ_ВЫХ) на выходе детектора относительно отношения сигнал/шум (СШ_ВХ) на его входе. При этом шум-фактор детектора ШФ=(СШ_ВХ) /(СШ_ВЫХ) уменьшается. То есть большой по амплитуде шум не подавляет слабый сигнал, как это происходит в линейных или квадратичных детекторах. Данное свойство нелинейных детекторов с ограничением используется в заявленном изобретении.

Кроме того, известны синхронные детекторы, являющиеся косинусным каналом квадратурных детекторов комплексного сигнала.

Данные синхронные детекторы представляют собой перемножитель напряжения сигнального канала (косинусной составляющей комплексного входного сигнала) и напряжения опорного канала. Эти детекторы также являются нелинейными детекторами с ограничением с присущим им свойством, описанным выше. Данные синхронные детекторы также используются в заявленном изобретении.

Первый независимый пункт изобретения.

Способ компенсации искажения доплеровского сигнала путём введения нелинейной по времени компенсирующей добавки в опорный сигнал оптимального фильтра.

Экспериментально обнаружено, что в космической радиолинии, созданной для радиолокации целей на дальности до1000 км, замечена сильная дисперсия по времени сигнала рассеянного космической целью, при этом искажается частота Доплера движущейся цели из-за влияния ионосферы. При создании оптимального фильтра подбирается частота Доплера модельного сигнала из матрицы априорно заданных частот. Этот модельный сигнал используется для алгоритма свёртки в согласованном фильтре. Величина искажения частоты Доплера заранее неизвестна по причине неопределённости параметров ионосферы. Определение этих параметров составляет самостоятельную сложную задачу (как, например системе ГЛОНАСС) и в этой заявке на изобретение не рассматривается.

Экспериментально обнаружен негативный эффект: свёртка в оптимальном (согласованном) фильтре принятого сигнала и модельного сигнала в виде ЛЧМ, когда частота Доплера модельного сигнала равна f_Д = k·t/2, где k - скорость линейного изменения доплеровской частоты из-за движения космического объекта (спутника), не даёт отклика корреляционной функции в наблюдаемых шумах. Поэтому для свёртки в оптимальном фильтре в виде добавки (a·t²) задаётся нелинейное по времени изменение частоты модельного (эталонного) сигнала f_Д почти повторяющего форму искажения доплеровского сигнала космической цели в виде:

f_Д = k·t/2+a·t²,

где k - скорость линейного изменения доплеровского ЛЧМ-сигнала (подбиралась для каждого космического объекта в процессе программирования до получения максимального отклика корреляционной функции типа свёртки),

a - коэффициент квадратичной добавки по времени из-за нелинейного искажения доплеровского сигнала в ионосфере (подбирался в процессе программирования до получения максимального отклика корреляционной функции типа свёртки),

t - текущее время.

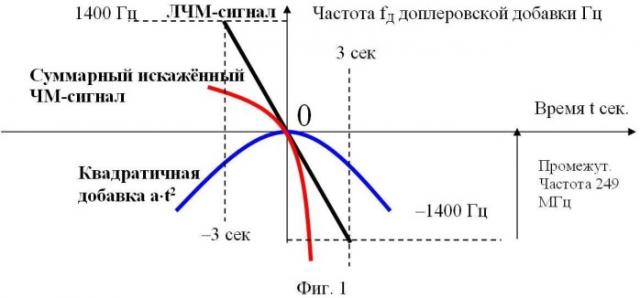
Качественный вид соотношения частот доплеровского ЛЧМ-сигнала, квадратичной добавки по времени и модельного суммарного искажённого сигнала приведён на схеме фиг. 1.

На схеме фиг. 1 показан конкретный экспериментальный результат, полученный в космическом бистатическом радиолокационном комплексе, где доплеровский ЛЧМ-сигнал космической цели в виде спутника имел значение 1400 Гц, время движение космической цели в барьере обнаружения 3 сек. Более подробное описание зафиксированных данных и результат их обработки приведены ниже в пункте доказательства реализуемости указанного способа. Для созданного оптимального фильтра выбран коффициент квадратичной добавки а=30, который подобран в процессе программирования оптимального фильтра по достижению максимального корреляционного отклика на выходе цифрового оптимального фильтра.

В связи с выше сказанным первый независимый признак изобретения на способ имеет нижеследующую формулировку.

Способ сложносоставной оптимальной фильтрации, реализующий компенсацию искажения доплеровской частоты космической радиолинии, состоящий в том, что опорный сигнал, используемый для процесса свёртки в оптимальном фильтре, содержит добавку, компенсирующую доплеровское искажение частоты космической радиолинии, отличающийся тем, что компенсирующая добавка является нелинейной функцией времени.

Второй независимый пункт изобретения.

Способ сложносоставной оптимальной фильтрации путём последовательной обработки сигнала сначала согласованным фильтром с когерентным накоплением сигнала, а затем фильтром с некогерентным мультипликативным накоплением сигнала в виде синхронного детектора.

В связи с тем, что в космических радиолиниях уровень сигнала в приёмнике на Земле мал и увеличение мощности спутниковых передатчиков ограничено масса-габаритными параметрами спутников, то актуальным является создание способов оптимальной фильтрации с подавлением шума более 60 дБ и уровнем вероятности ошибок не хуже 10^-10. Как указано во введении, простое применение помехозащитного кодирования информации не даёт желаемого результата, так как это кодирование требует точного знания доплеровского сдвига частоты спутникового передатчика или частоты рассеянного сигнала космической цели в радиолокации. Образуется замкнутый круг: обнаружение и измерение амплитуды слабого сигнала на Земле в оптимальном фильтре требует точного знания доплеровского сдвига частоты и искажения этого сигнала, например ионосферой, но точное измерение частоты требует точного измерения амплитуды слабого сигнала, что возможно только путём сильного подавление шума, который намного выше амплитуды сигнала. Здесь выполняется известный в теории информации принцип неопределённости, аналогичный принципу неопределённости Гейзенберга в квантовой механике. Как известно, чтобы обойти это противоречие применяют принцип многоканального оптимального приёма [7], причём параллельные в пространстве и времени синхронные и синфазные каналы могут быть созданы путём многочастотного разделения каналов или путём многокодового разделения каналов (как в ГЛОНАСС или GPS), или тем и другим способом вместе, т.е. многочастотным и многокодовым (как в космическом телевидении высокой чёткости на 3000 или 6000 поднесущих частотах при двухслойном помехозащищающем кодировании ортогональными кодами Рида-Соломона на каждой поднесущей). Эти методы имеют свои преимущества и недостатки и их рассмотрение не в ходит в в задачу описания изобретения на способ в данной заявке.

В данной заявке предлагается альтернативный способ эффективного подавления помехи, базирующийся на описанном выше свойстве нелинейных детекторов с ограничением увеличивать отношение сигнал/шум. Подробно принцип действия сложного оптимального фильтра с такого типа детекторами описан ниже в пункте "описания принципа работы". Сущность второго независимого пункта на способ состоит в следующем.

Способ сложносоставной оптимальной фильтрации слабого сигнала, состоящий в том, что входной сигнал с шумом фильтруется в согласованном фильтре с когерентным накоплением сигнала с последующим преобразованием в детекторе с некогерентным аддитивным накоплением корреляционных откликов, отличающийся тем, что, во-первых, в процессе согласованной фильтрации с когерентным накоплением сигнала вносится частотная добавка нелинейная по времени, компенсирующая частотные искажения сигнала как по первому независимому пункту изобретения, во-вторых, выходной корреляционный отклик согласованного фильтра подвергается нелинейному преобразованию типа нелинейного взвешивания с ограничением и, в-третьих, сигнал после нелинейного взвешивания преобразуется по методу синхронного детектирования с некогерентным мультипликативным накоплением корреляционных откликов.

Описание метода сложносоставной оптимальной фильтрации.

Описание метода сложносоставной оптимальной фильтрации слабого сигнала приводится на конкретном экспериментально проверенном примере работы космического бистатического комплекса, в котором был использован этот способ фильтрации сигнала. Данный комплекс представлял собой радиолокационную систему наземно-космического базирования, в которой передатчик с излучающей антенной устанавливался на спутнике, двигающемся по высоко эллиптической орбите (ВЭО) или геостационарной орбите (ГСО), а высоко чувствительный приёмник с приёмной антенной находился на Земле. Схема организации бистатической радиолинии показана на фиг. 2. Задача космического бистатического радиолокатора обнаружить дифракционный (просветный) сигнал от пролётающего КО в в бистатической зоне обнаружения радиолокатора. Просветный сигнал в общей 3-децибельной зоне ДН КО и 3-децибельной зоне ДН НА образует зону обнаружения КО по её просветному лучу (рассеянному излучению вперёд вдоль направления распространения падающей электромагнитной волны от передатчика).

На фиг. 2 обозначено: 1 - наземная приёмная антенна, 2 - космический объект, обнаруживаемый в КРК, 3 - передающая антенна космического аппарата (спутника на ВЭО или ГСО), ДН КА - диаграмма направленности передающей антенны космического аппарата, ДН НА - сканирующая диаграмма направленности приёмной наземной антенны, ДН КО - диаграмма направленности дифракционного рассеяния космическим объектом электромагнитного излучения антенны 3, КО является пассивным ретранслятором излучения антенны КА, R₁ - наклонная дальность от наземной антенны 1 до КО, R₂ - наклонная дальность от КО до антенны 3 космического аппарата, "бистатическая линия" - ось в пространстве, соединяющая фазовые центры антенны КА и наземной антенны, а эллипсоидальная область вокруг этой оси определяет область обнаружения КО космическим бистатическим радиолокатором.

В эксперименте использовалась наземная приёмная параболическая антенна на длину волны порядка λ ~ 0,1 м диаметром D=25 м с шириной диаграммы направлнности (ДН НА) порядка θ_пр ~ 0,3 град и коэффициентом направленного действия (КНД_пр)

КНД_пр ≈ (π·D/λ)² = 360000=55дБ. (1)

Космическая передающая антенна спутника в виде ФАР имеет ширину ДН, равную θ_пер ≈6 град, а её соответствующий КНД

КНД_пер ≈ 890= 29 дБ. (2)

Ширина ДН просветного луча обнаруживаемого космического объекта имеет максимальную величину θ_ка = 3 град и минимальную величину Δθ_ка = 1 град, тогда соответствующий бистатическая БКНД_ко бистатической эффективной поверхности рассеяния (БЭПР) теневого поперечника этого КО равна

БКНД_ко = 3560 ÷32000 =36 дБ ÷45 дБ,

а соответствующая теневая площадь КО равна

S_ко = БКНД_ко·λ² /4π= (3560 ÷32000) 0,13²/4π= (4,8÷43) м²≈ 5 м² (минимально обнаружимая площадь теневого контура КО),

следовательно БЭПР (бистатическая ЭПР) этого КО равна:

БЭПР_ко= БКНД_ко·S_ко , т.е.

БЭПР_ко = (3560 ÷32000)·(4,8 ÷43)≈ (17100 ÷1380000) м².

Мощность СВЧ-излучения передающей антенны равна 10 Вт.

Наклонная дальность от наземного приёмника до КО

R₁=10⁶ м, (3)

наклонная дальность от КО до спутникового передатчика КА

R₂ =39·10⁶ м. (4)

По формуле радиолокации для мощности мнимального принимаемого P_пр сигнала (когда БЭПР_ко минимальна) принимает вид: при S_ка≈ 5 м², P_пер=1 Вт,

P_пр = P_пер· КНД_пер· S_ко ² · КНД_пр/[(4π)²· R₁ ² · R₂ ²] =

=365000·5²·890/[4² ·π² ·10¹²·39² ·10¹²] ≈

≈ 3,65·10⁵·5²·9·10²/(16·9,86·10¹²·1,5·10³· 10¹²)=0,38·10^-19Вт= -194 дБВт. (5)

Собственный тепловой шум цифрового приёмного тракта на входе оптимального фильтра после антенного малошумящего усилителя (МШУ) с эффективной температурой T_Э = 40К равен

P_ШТ= k·T_Э·F = -188 дБВт, (6)

где k =1,38·10^-23 Вт/Гц - постоянная Больцмана,

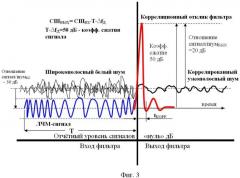
F~ 3000 Гц - эффективная полоса частот оптимального фильтра, настроенного на пропускание полосы доплеровских частот просветного ЛЧМ-сигнала при пролёте космическим объектом по области обнаружения космического бистатического радиолокатора. Сравнив P_ШТ и P_пр, видно, что минимальный сигнал находится ниже теплового шума цифрового приёмного тракта на 6 дБ, но при экспериментах с конкретным спутниковым передатчиком выяснилось, что на входе МШУ шумы СВЧ-передатчика ещё на 24 дБ больше указанных выше тепловых шумов, так что суммарный шум превышал просветный сигнал от КО на 30 дб, то есть отношение сигнал/шум= -30 дБ. Следовательно, чтобы обеспечить отношение сигнал/шум= +20 дБ при вероятности ошибки не хуже 10^-11 необходимо подавить шум на 50 дБ, что решается способом сложносоставной оптимальной фильтрации. Схема общего метода оптимальной фильтрации показана на фиг. 3.

Согласно теории оптимальной обработки сигнала [7], вероятность правильного обнаружения определяется величиной отношения сигнал-шум на выходе оптимального приёмника или оптимального фильтра применительно к созданной системе измерения просветного сигнала. Это отношение рассчитывается по формуле:

СШ_ВЫХ= СШ_ВХ·Т / t_КОРР,

где обозначено

СШ_ВЫХ = P^ВЫХ / P_Ш ^ВЫХ - отношение мощности P^ВЫХ выходного сигнала оптимального фильтра к мощности P_Ш ^ВЫХ выходного шума оптимального фильтра,

СШ_ВХ = P^ВХ / P_Ш ^ВХ - отношение мощности P^ВХ входного сигнала на входе оптимального фильтра к мощности P_Ш ^ВХ входного шума оптимального фильтра,

Т - время накопления входного сигнала или длительность импульса доплеровского просветного ЛЧМ-сигнала равная времени пролёта КО бистатической зоны обнаружения,

t_КОРР - время корреляции выходного шума фильтра,

или указанное отношение равно

СШ_ВЫХ= СШ_ВХ·Т·Δf_Д, (7)

где

Т· Δf_Д - коэффициент сжатия или база сигнала оптимального фильтра,

Δf_Д = 2·f_Д = 1/ t_КОРР - полоса изменения доплеровской частоты f_Д просветного ЛЧМ-сигнала,

Схематически действие оптимального фильтра по сигналу показано на фиг. 3. На схеме отражён тот факт, что по формуле радиолокационной дальности бистатической радиолокации максимальная дальность R₁ достигается при минимальной (пороговой) входной мощностью P^ВХ _MIN оптимального приёмника или оптимального фильтра. Эта формула имеет вид

(R₁·R₂)² = P_ПЕР·К_ПЕР·S_КО ²·К_ПР / (16π²·P^ВХ _MIN)

или с учётом (7) P^ВХ _MIN= СШ_ВЫХ·P_Ш ^ВХ/(Т·f_Д) эта формула дальности принимает стандартный вид:

(R₁·R₂)² = P_ПЕР·К_ПЕР·S_КО ²·К_ПР·(Т·f_Д) / (16π²·СШ_ВЫХ ·P_Ш ^ВХ),

где заданные в эксперименте значения обозначены как

R₁- наклонная дальность по линии «антенна КП-КО»,

R₂ - наклонная дальность по линии «КО-антенна КА»,

P_ПЕР - мощность передатчика КА,

К_ПЕР - коэффициент усиления передающей антенны КА,

S_КО - площадь теневого контура КО,

К_ПР - коэффициент усиления приёмной антенны КП.

Задача оптимального фильтра двоякая: обеспечить приём малой входной пороговой мощности P^ВХ _MIN для достижения большой дальности и обеспечить требуемое высокое выходное отношение сигнал/шум СШ_ВЫХ для получения высокой вероятности обнаружения или минимальной вероятности ошибки приёма. Это задача решается заданием времени Т накопления входного ЛЧМ-сигнала и полосы доплеровских частот Δf_Д сжатого выходного сигнала фильтра, причём величина 1/Δf_Д определяет время корреляции выходного шума фильтра. Поскольку энергия сигнала на входе и выходе фильтра одинакова (по определению оптимального фильтра) и мощность шума также не меняется, то высокий уровень выходной мощности обеспечивается перераспределением энергии сигнала на выходе в импульс малой длительности порядка t_КОРР~1/Δf_Д в широкой частотной полосе Δf_Д с коэффициентом сжатия К_СЖ=Т·Δf_Д, который входит в числитель формулы радиолокационной дальности указанного выше стандартного вида.

В условиях описанных экспериментов значения дальностей R₁, R₂ и параметров Т и Δf_Д задаются прогнозом пролёта обнаруживаемых КО, поэтому максимально достижимое значение СШ_ВЫХ однозначно определяется по формуле вероятности ошибки (ВО) обнаружения КО по измеренному в эксперименте уровню мощности входного шума P_Ш ^ВХ с учётом способа модуляции (кодирования) принимаемого сигнала, в данном случае доплеровской линейно-частотной модуляцией просветного сигнала:

ВО= Ф(СШ_ВЫХ), где Ф - нормированный интеграл вероятности ошибки.

Таким образом параметры синтезированного оптимального фильтра однозначно определяют возможность обнаружения различных КО различной площади теневого контура с заданной вероятностью ошибки обнаружения.

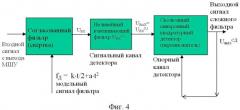
Блок схема алгоритма работы реализованного сложносоставного оптимального фильтра показана на фиг. 4.

В качестве когерентного накопителя использовался описанный выше согласованный фильтр с компенсацией искажения ионосферой доплеровской частоты КО путём введения квадратичной по времени добавки a·t² к модельному ЛЧМ-сигналу f_Д = k·t/2 (см. фиг. 4), а в качестве мультипликативного некогерентного накопителя использовался синхронный квадратурный детектор комплексного выходного сигнала когерентного (согласованного) фильтра. При этом в компьютерном алгоритме детектора на первый сигнальный вход детектора подавался текущий выходной сигнал U_вых когерентного накопителя (корреляционный отклик фильтра) с нелинейным взвешиванием в виде корня десятой степени из U_вых ^0,1 с помощью взвешивающего фильтра (см. фиг. 4). На второй опорный вход детектора подавались по положительной обратной связи все предыдущие мультипликативно накопленные выходные комплексные сигналы этого некогерентного накопителя во всех предыдущих сдвигах входного окна согласованного фильтра (когерентного накопителя) длительностью времени свёртки Т= 6 сек, равного времени пролёта КО по области обнаружения радиолокатора. Напряжение U_вых ^СД на выходе некогерентного мультипликативного накопителя (синхронного детектора) на N-шаге накопления равно итерактивному произведению (по цепи обратной связи)

(U_вых ^СД)_N =(U_вых ^0,1)_N·[(U_вых ^0,1)_N-1· (U_вых ^СД)_N-1]·cos(Δφ_N,N-1),

где разность фаз Δφ_N,N-1≈0 и cos(Δφ_N,N-1)≈1 для двух последовательных комплексных корреляционных откликов (U_вых ^0,1)_N и (U_вых ^0,1)_N-1, так как фазы комплексных корреляционных функций согласованного фильтра не меняются по фундаментальному свойству этих фильтров, а начальное значение произведения [(U_вых ^0,1)₀· (U_вых ^СД)_о] =1 по определению мультипликативного накопления. Важно отметить, что функциональный вид нелинейного взвешивающегофильтра не приципиален, лишь бы это была функция с ограничением сигнала, например arctg(U) или другая подобная, даже не аналитическая функция.

Результирующее отношение сигнал/шум детектора возрастало более чем на 20 дБ. Программа обработки записанной информации методом сложносоставного оптимального фильтра приведена в ПРИЛОЖЕНИИ А и реализована на языке MATLAB файле WinradHD_ARIANE_sinhronDETEC.m.

Доказательство реализуемости способа сложносоставной оптимальной фильтрации.

С целью доказательства реализуемости прннципа работы космического радиолокатора был создан бистатический радиолокационный комплекс с антеннами, передатчиками, приёмниками и цифровой обработкой сигналов, параметры которых описаны выше. Работа системы обработки информации доказала реализуемость предлагаемого в заявке способа сложносоставной оптимальной фильтрации просветного сигнала КО, пролетающего через бистатическую область обнаружения.

Были проведены многочисленные эксперименты по настройке различных оптимальных фильтров и исследованию их функционирования по обнаружению просветного сигнала была проведена серия заключительных контрольных экспериментов с типовыми КО с большой площадью теневого контура порядка 20 м², с средней площадью теневого контура порядка 6 м² и КО с малой площадью теневого контура не более 3 м³. Эти космические объекты перечислены в таблице 1.

В данном разделе с целью сокращения количества демонстрационных материалов для сравнения приведены характерные примеры КО с самой большой площадью теневого контура типа разгонного блока ARIANE-5 и КО с самой маленькой теневой площадью типа геофизического спутника NOAA-3, которые убедительно доказывают реализуемость способа.

Условия эксперимента: диаграмма направленности приёмной антенны - сопровождение КО узкой ДН, шириной порядка 0,3⁰ , регистратор - измерительный радиоприёмник из состава аналого-цифрового комплекса с АЦП на промежуточной частоте 249 МГц на базе мониторингового цифрового радиоприёмника Rs-Rus.

Порядок проведения эксперимента: сначала включается режим сопровождения наземной антенной выбранного по прогнозу КО, затем с отключённым мониторинговым радиоприёмником от антенного МШУ измеряется уровень собственных шумов этого радиоприёмника с его выхода по спектрограмме и по "водопадному преобразованию" на экране компьютера с помощью программы Winrad. Затем на вход измерительного радиоприёмника подаётся сигнал с выхода МШУ и записывается суммарный шум МШУ и приёмника Rs-Rus, а эатем производится запись дифракционного сигнала от пролёта КО.

Результаты измерений собственного шуму приёмника Rs-Rus приведёна на фиг. 5.

На фиг. 5 видно, что уровень собственных шумов приёмника Rs-Rus равен -140 дБВт в полосе 40 кГц с учётом его шум-фактора 6 дБ. Коэффициент усиления этого измерительного радиоприёмника установлен равным 1. После подключения этого радиоприёмника к выходу МШУ измерялся суммарный прямой и просветный сигнал по УДН, когда он должен был появится в соответствии с прогнозом.

Запись сигнала от разгонного блока ARIANE-5.

В момент прохождения КО и сопровождающей его оси ДН наземной антенны через максимум ДН антенны передатчика КА (оси антенна КП-антенна КА) наблюдается максимальный отклик на "водопадной диаграмме" на фиг. 6 и спектрограмме на фиг. 7.

На фиг. 6 и 7 обнаруживается прямой сигнал (просветного сигнала не видно в шумах) вблизи несущей частоты f=249011 кГц передатчика КА с медленно изменяющейся спутниковой доплеровской добавкой примерно 2 Гц/сек. Обращает внимание тот факт, что в момент прохождения оси "антенна КП-антенна КА" наблюдается максимум прямого сигнала на уровне -50 дБВт на частоте 249011 кГц и помеховое излучение на боковых частотах 249011±2,3 кГц с локальным максимумом мощности на уровне -91 дБВт. То есть превышение прямого сигнала над помехой не более 41 дБ. Следует отметить важный факт, что полоса доплеровского сигнала по прогнозу равна Δf_Д=2880 Гц (девиация этой частот f_Д=±1440 Гц), поэтому помеховый сигнал не мешает обнаружению КО в указанной полосе частот, меньшей, чем полоса частот помехи, кроме того, в процессе оптимальной обработки спектр помехового сигнала будет дополнительно вычитаться программно из суммарного сигнала (помеха+просветный сигнал).

Наблюдается периодическое изменение амплитуды сигнала на 2÷3 дБ с периодом 10÷12 сек, по-видимому, из-за известных крайне низкочастотных (КНЧ) и ультранизкочастотных (УНЧ) колебаний проницаемости ионосферы, такие колебания прослеживаются на всех записанных файлах.

В соответствии с прогнозом время пролёта КО барьера обнаружения равно 5 сек. Высота КО равная 768 км и почти равна наклонной дальности КО, так как высота места КА почти 84 град.

Замечания: Просветный сигнал для площади теневого контура порядка 24 м² теоретически имеет уровень мощности на наземной антенне -185 дБВт, а прямой сигнал равен -108 дБВт. Следовательно, теоретическое отношение прямой сигнал/просветный сигнал равно 77 дБ. После усиления на 70 дБ экспериментально наблюдаемый прямой сигнал равен -50 дБВт (-38 дБВт-12 дБВт) с учётом суммарного шум-фактора равного 12 дБ ( МШУ, ПУПЧ, приёмника Rs-Rus), просветный сигнал находится на уровне -120 дБВт. Так как экспериментально наблюдаемый уровень шума равен -110 дБВт, то просветный сигнал теоретически ниже уровня шума на 10 дБ.

Анализ результатов для данного КО и всех последующих КО проводился после оптимальной обработки записанного сигнала. Алгоритм обработки и подбора параметров фильтров одинаков для всех КО.

Анализ параметров сигнала нестабилизированного КО типа разгонного блока ARIANE-5

После оптимальной обработки в оптимальном фильтре с коэффициентом квадратичной добавки a = 30 получена функция корреляционного отклика при пролёте КО вблизи оси «антенна КП-антенна КА» с максимальной амплитудой, показанной на фиг. 8. Обработка проводилась в частотной области, используя БПФ по Nz=32768 точкам в окне времени Т=6 сек (по прогнозу время пролёта главного лепестка просветного сигнала равно 5 сек), сдвиг окна производился через Nz/16=2048 точек или время Т/16= 0,375 сек для поиска максимума сигнала. Весь файл записи в течение 4 мин объёмом 20 МВ предварительно просматривался визуально для поиска во времени участка с максимальным прямым сигналом при положении КО вблизи оси «антенна КП-антенна КА» в области 28 сек при девиации ± 14 сек относительно максимального сигнала. Затем файл разбивался на 10 файлов по 2 МБ и выбирался файл, содержащий найденную область с максимальным прямым сигналом по времени. Это время совпадало с точностью ± 1 сек с прогнозным временем нахождения КО в барьере обнаружения. Затем именно этот файл подвергался оптимальной обработке.

На фиг. 8 показаны графики сигналов при положения КО до подлёта к оси «антенна КП-антенна КА».

На нижнем графике фиг. 8 показана максимальная амплитуда отклика просветного сигнала 14÷15 дБ над шумом в виде корреляционной функции на отметке времени 0,6 сек от конца пролёта КО в течение 6 сек. Видна тонкая структура просветного сигнала при дифракции на КО. На среднем рисунке показана спектрограмма выходного сигнала фильтра, а его АЧХ показана на фиг. 11, которая не совпадает со стандартной АЧХ фильтра доплеровского ЛЧМ-сигнала. На верхнй фиг. 8 показан график линии зашумленного просветного сигнала на выходе приёмника Rs-Rus визуально закрашенный сплошным красным цветом в полосе частот 40 кГц. Синяя линия показывает нелиейно частотно модулированный модельный сигнал, а его АЧХ приведена на фиг. 11. На фиг. 9 показаны те же линии, что и на рисунке 2.36, но для случая расположения центра окна, а, следовательно, и КО на оси «антенна КП-антенна КА».

Из этого рисунка видно, что при положении КО на этой оси доплеровский сдвиг частоты КО относительно доплеровской частот КА равен прогнозируемому нулю и корреляционный отклик отсутствует.

На фиг. 10 показаны те же графики, но после пролёта КО оси «антенна КП-антенна КА» форма корреляционнй функции не совпадает с её формой до подлёта к этой оси (см. фиг. 8), что говорит о несимметричноститеневого контура КО. Максимум отклика равен 14 дБ над шумом.

На фиг. 11 видно, что АЧХ фильтра кардинально отличается от АЧХ оптимального фильтра с модельным ЛЧМ-сигналом. Именно эта АЧХ участвует в образовании свёртки с зашумленным просветным сигналом при использовании БПФ.

С целью исследования возможности более раннего обнаружения КО

вне области Т=6 сек (по прогнозу Т= 5 сек), т. е. вне главного лепестка просветного сигнала, проводилась свёртка начиная с времени -14 с до момента положения КО на оси «антенна КП-антенна КА». Результат свертки показан на фиг. 12. На верхней части этого рисунка красным цветом показан весь принятый сигнал в течение 28 сек, тот же, что на фиг. 6 - 8. Однако по программе модельный сигнал (график чёрного цвета) сдвигается вдоль графика принятого сигнала с шагом Nz/16, поэтому отклик о