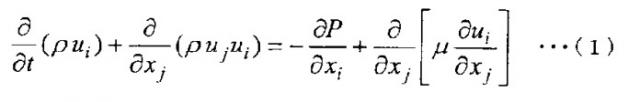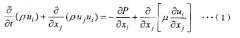Способ вычисления физического значения, способ численного анализа, программа вычисления физического значения, программа численного анализа, устройство вычисления физического значения и устройство численного анализа

Способ вычисления физического значения, способ численного анализа, программа вычисления физического значения, программа численного анализа, устройство вычисления физического значения и устройство численного анализа

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ

Настоящее изобретение относится к способу вычисления физического значения, способу численного анализа, программе вычисления физического значения, программе численного анализа, устройству вычисления физического значения и устройству численного анализа.

ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ

В известном уровне техники в качестве способов численного анализа для распределения скоростей потока, распределения напряжений, распределения тепла и т.п. посредством численного анализа известные методики включают в себя метод конечных элементов, метод конечных объемов, метод вокселей и метод частиц.

Обычно такой способ численного анализа строится из предварительного процесса, решающего процесса и заключительного процесса. Тогда предварительный процесс формирует модель расчетных данных. Затем решающий процесс вычисляет вышеупомянутые физические значения с использованием модели расчетных данных и основного уравнения, подвергнутого дискретизации (в дальнейшем называемого дискретизированным основным уравнением).

Например, в традиционном методе конечных объемов область анализа делится на множество областей. Затем физические значения в каждой разделенной области вычисляются с использованием объема каждой разделенной области, площади граничной поверхности между соседними разделенными областями и вектора нормали к граничной поверхности.

В методе конечных объемов предварительный процесс формирует модель расчетных данных (обычно называемую сеткой), содержащую координаты вершин (Вершина) каждой разделенной области. Затем решающий процесс вычисляет объем вышеупомянутой разделенной области, площадь граничной поверхности и вектор нормали к граничной поверхности, используя Вершину и т.п., содержащуюся в модели расчетных данных, а затем вычисляет физические значения с использованием этих значений. Вершина указывает значения для определения геометрической формы разделенной области. Таким образом, признается, что в методе конечных объемов решающий процесс вычисляет объем разделенной области, площадь граничной поверхности и вектор нормали к граничной поверхности с использованием геометрической формы разделенной области.

Дополнительно в методе конечных объемов может предоставляться часть, где частично не выполняется условие совместного использования вершин для соседних разделенных областей. Таким образом, в методе конечных объемов ограничение на разделенную область отчасти смягчается в некоторых случаях. Тем не менее, тип элемента для анализа, который нужно использовать, ограничивается, например, четырехгранным элементом, шестигранным элементом, призменным элементом и пирамидальным элементом.

Здесь, как показано в Патентном документе 1, также предложен метод конечных объемов без ограничения типа элемента для анализа. Тем не менее, даже в таком методе конечных объемов без ограничения на тип элемента для анализа, аналогично традиционному методу конечных объемов, описанному выше, предварительный процесс формирует модель расчетных данных, содержащую координаты вершин (Вершина) каждой разделенной области, а затем решающий процесс вычисляет физические значения с использованием Вершины, содержащейся в модели расчетных данных.

Дополнительно, как широко известно, метод конечных элементов является способом вычисления физических значений в каждой разделенной области с использованием интерполирующей функции. Однако, аналогично методу конечных объемов, решающий процесс использует геометрическую форму разделенной области, определенную Вершиной и т.п.

Метод вокселей и метод частиц являются способами численного анализа, допускающими простое формирование модели расчетных данных по сравнению с методом конечных элементов и методом конечных объемов.

Метод вокселей является способом, в котором данные вокселей для задания области анализа с использованием множества вокселей (прямоугольная сетка), имеющих форму прямоугольного параллелепипеда и в основном один и тот же размер, формируются в виде модели расчетных данных, и вычисление физических значений выполняется с использованием данных вокселей, так что выполняется численный анализ. Методы вокселей схематически делятся на тип со взвешенной невязкой, который использует основное уравнение на основе метода взвешенных невязок, и тип без интегрирования, который использует модель клеточного автомата, решеточную модель Больцмана или т.п. Тогда, в соответствии с этим методом вокселей, не нужна Вершина и т.п., которую нужно использовать в качестве данных вокселей.

В соответствии с таким методом вокселей, область анализа задается просто путем разделения области анализа на воксели. Таким образом, модель расчетных данных формируется за короткое время.

С другой стороны, метод частиц является способом, в котором данные частиц формируются в виде модели расчетных данных для задания области анализа с помощью множества частиц, и вычисление физических значений выполняется с использованием этих данных частиц, так что выполняется численный анализ. Метод частиц, относящийся к типу без интегрирования, использует модель межчастичного взаимодействия в качестве основного уравнения. Метод частиц не содержит разделенные области и поэтому не требует Вершины и т.п. Таким образом, в соответствии с таким методом частиц область анализа легко задается путем равномерного распределения частиц в области анализа, так что модель расчетных данных формируется за короткое время.

ИЗВЕСТНЫЙ УРОВЕНЬ ТЕХНИКИ

ПАТЕНТНЫЙ ДОКУМЕНТ

Патентный документ 1: Описание изобретения в опубликованной заявке на патент США № 2008/0021684

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

ПРОБЛЕМЫ, КОТОРЫЕ ДОЛЖНЫ БЫТЬ РЕШЕНЫ ПОСРЕДСТВОМ ИЗОБРЕТЕНИЯ

В случае, где геометрическая форма каждой разделенной области используется в решающем процессе, как в традиционном способе численного анализа, например методе конечных элементов и методе конечных объемов, очевидно, что модель расчетных данных обязательно содержит данные, описывающие геометрическую форму разделенной области.

С целью задания геометрической формы разделенной области необходима вершинная связность (Связность Вершины; в дальнейшем называемая Связностью (Connectivity)) в дополнение к Вершине. Таким образом, в методе конечных элементов и методе конечных объемов необходимо, чтобы модель расчетных данных содержала Вершину и Связность.

Здесь, в частности, Связность определяется с помощью информации о соответствии общих номеров узлов, последовательно заданных вершинам всех разделенных областей, и локальных номеров узлов, последовательно заданных вершинам в одной разделенной области.

Как широко известно, модель расчетных данных, содержащая такую Вершину и Связность, требует весьма большой работы для формирования.

Например, в модели расчетных данных, используемой в методе конечных элементов, модель расчетных данных нужно формировать так, что должно выполняться условие, по которому соседние разделенные области всегда совместно используют Вершину, как показано на фиг. 1. Таким образом, чтобы все разделенные области выполняли это условие, необходимо довольно большое время.

С другой стороны, в модели расчетных данных, используемой в методе конечных объемов, допускается наличие Вершины, не используемой совместно соседними разделенными областями, как показано на фиг. 2. Это увеличивает гибкость формирования сетки по сравнению с методом конечных элементов. Тем не менее, даже в методе конечных объемов модель расчетных данных нужно формировать на условиях, что не используемая совместно Вершина располагается, по меньшей мере, на границе соседних разделенных областей, и что форма разделенной области обычно совпадает с типом элемента для анализа, установленным заранее. Таким образом, сложно сказать, что гибкость формирования сетки является высокой.

Более того, в последние годы численный анализ выполняется в области анализа, извлеченной из данных о трехмерной форме, например данных трехмерной CAD (системы автоматизированного проектирования). Тем не менее, данные о трехмерной форме не являются данными, сформированными для численного анализа. Таким образом, содержатся данные, которые указывают перекрывающиеся поверхности, пересечение поверхностей, зазоры между поверхностями, небольшое отверстие и т.п. То есть включается много условий, которые не подходят для формирования модели расчетных данных, содержащей Вершину и Связность. Таким образом, чтобы разрешить формирование модели расчетных данных, содержащей Вершину и Связность, данные о трехмерной форме нужно модифицировать или изменить. Тогда, чтобы разрешить модификацию или изменение данных о трехмерной форме с целью формирования модели расчетных данных, содержащей Вершину и Связность, нужно выполнить довольно большую ручную работу, которая требует опыта и метода проб и ошибок. Это порождает большую проблему во время практического использования метода конечных элементов или метода конечных объемов.

Кроме того, как и в методе конечных объемов, в случае, когда решающий процесс вычисляет объем разделенной области, площадь граничной поверхности и вектор нормали к граничной поверхности, объем вычисления дополнительно увеличивается в решающем процессе, так что вычислительная нагрузка на решающий процесс дополнительно увеличивается.

В методе вокселей модель расчетных данных можно сформировать за короткое время. Тем не менее, возникает следующая проблема. В методе вокселей область анализа задается в основном вокселями (прямоугольная сетка), имеющими одинаковый размер. В общем, в методе конечных элементов и методе конечных объемов размер элемента (размер каждой разделенной области) устанавливается небольшим в области, где нужна более высокая точность анализа, чтобы вычисление физических значений точно выполнялось в этой области. Более того, размер элемента для другой области устанавливается большим, чтобы уменьшалась вычислительная нагрузка для этой области. Тем не менее, в методе вокселей все воксели в основном имеют один и тот же размер. Таким образом, когда воксели задаются небольшими, вычислительная нагрузка становится весьма большой. В отличие от этого, когда воксели задаются большими, точность анализа ухудшается.

Дополнительно в методе вокселей каждую область анализа нужно задавать путем размещения вокселей (прямоугольная сетка), имеющих одинаковый размер. Таким образом, область анализа не может быть гладкой возле границы с внешней областью, и поэтому в некоторых случаях образует ступенчатую форму. То есть, даже когда фактическая область, которую нужно проанализировать, содержит наклонную плоскость, искривленную поверхность или т.п., область представляется в ступенчатой форме в данных вокселей. Таким образом, форма области анализа в методе вокселей становится отличной от фактической формы области, которую нужно проанализировать. Это ухудшает точность анализа.

Соответственно, предложен усовершенствованный способ, называемый методом скошенных ячеек, в котором ступенчатая область в данных вокселей обрезается по наклонной плоскости или искривленной поверхности (коррекция границы), присутствующей в фактической области, которую нужно проанализировать. Тем не менее, в этом усовершенствованном способе коррекция границы легко формирует весьма небольшие разделенные области. В таком случае, когда формируются такие небольшие разделенные области, точность анализа ухудшается.

Дополнительно в этом усовершенствованном способе формирование скошенных ячеек и решающий процесс используют Вершину.

Как описано выше, метод вокселей без коррекции границы не требует Вершины и т.п. Тем не менее, существует ограничение в формировании вокселей, то есть в так называемом формировании сетки. А именно, когда необходима достаточная точность анализа, количество вокселей увеличивается, и также увеличивается вычислительная нагрузка в решающем процессе. Это порождает проблему. Более того, в результате в усовершенствованном способе по методу вокселей с коррекцией границы становится необходимой Вершина. Таким образом возникает влияние геометрической формы разделенных областей. В результате весьма большая ручная работа, требующая опыта и метода проб и ошибок, становится необходимой для обработки по формированию разделенных областей возле границы с внешней областью. Таким образом, модель данных формы не может быть сформирована за короткое время.

С другой стороны, метод частиц требует вычисления отношения связи конкретной частицы с другими частицами. Таким образом, нужно искать частицы, присутствующие в окрестности конкретной частицы. Затем эти алгоритмы ближнего соседа частицы выполняются над всеми частицами в принципе. Тем не менее, в методе частиц каждая частица движется в зависимости от времени и поэтому отношение связи между частицами всегда меняется. Таким образом, алгоритмы ближнего соседа нужно выполнять в каждый момент изменения времени при анализе. Это вызывает увеличение вычислительной нагрузки. Таким образом, предпринята попытка, чтобы аккуратно выбирать частицы, над которыми должен выполняться поиск соседства, чтобы уменьшалась вычислительная нагрузка в алгоритмах ближнего соседа. Тем не менее, например, когда количество частиц увеличивается с целью повышения точности анализа, вычислительная нагрузка увеличивается пропорционально квадрату количества частиц.

В таком методе частиц, чтобы численный анализ был осуществлен в рамках практического времени, необходимо использовать большое количество CPU (центральных процессорных модулей) в большой машине параллельной обработки данных. Например, в реальном случае вычисление, завершенное за половину дня обычным решающим устройством по методу конечных объемов, использующим Вершину и Связность на одном CPU, заняло больше одной недели у метода частиц, применяющего параллельное вычисление с использованием 32 CPU.

Кроме того, даже в методе частиц, когда частицы плотно размещаются, вычислительная нагрузка увеличивается значительно. Когда частицы размещаются небрежно, точность анализа ухудшается.

Дополнительно, как подробно описано позже, в методе частиц, когда анализируется физическое явление, например текучая среда, структура, тепло и диффузия на основе закона сохранения физического значения, сохранение выполняется не полностью.

Например, отсутствует информация касательно площади, занимаемой на граничной поверхности частицей, размещенной так, чтобы быть обращенной к граничной поверхности между областью анализа и внешней областью. Таким образом, даже когда нужно ввести условие, что тепло поступает через граничную поверхность, количество тепла, введенное в каждую частицу, не распознается точно. Таким образом, не получается точное количественное значение.

Настоящее изобретение разработано в связи с проблемами в традиционных способах численного анализа, описанных выше, таких как метод конечных элементов, метод конечных объемов, метод вокселей, усовершенствованная методика в методе вокселей и метод частиц. Цель настоящего изобретения - снизить рабочую загрузку при формировании модели расчетных данных и снизить вычислительную нагрузку в решающем процессе, не вызывая ухудшения точности анализа.

РЕШЕНИЕ ПРОБЛЕМ

Чтобы решить вышеупомянутую проблему, настоящее изобретение применяет конфигурацию способа вычисления физического значения для вычисления физических значений в способе численного анализа для численного анализа физического явления, содержащем этап вычисления физических значений, состоящего в вычислении физических значений в области анализа, разделенной на множество разделенных областей, не ограниченных формой прямоугольной сетки, где на этапе вычисления физических значений физические значения вычисляются с использованием дискретизированного основного уравнения, которое использует значения, не требующие координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность) и которое выводится на основе метода взвешенных невязок; и модели расчетных данных, в которой объемы разделенных областей и характеристические значения граничной поверхности, указывающие характеристики граничных поверхностей соседних разделенных областей, предоставляются в виде значений, не требующих координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность).

Дискретизированное основное уравнение, используемое в настоящем изобретении, не является традиционным уравнением, выраженным в виде, содержащем значения (Вершина и Связность), которые определяют геометрическую форму каждой разделенной области, а является уравнением, не требующим значений, которые определяют геометрическую форму каждой разделенной области. Дискретизированное основное уравнение, используемое в настоящем изобретении, получается путем намеренной остановки посередине процесса выведения, на основе метода взвешенных невязок, традиционного уравнения, использующего значения, которые определяют геометрическую форму. Такое дискретизированное основное уравнение, используемое в настоящем изобретении, выражается в значениях, не требующих геометрической формы разделенной области (то есть значениях, не требующих Вершины и Связности), и тогда может выражаться в виде, например, зависящем исключительно от двух вещей: объема разделенной области и характеристического значения граничной поверхности.

То есть в традиционном методе конечных элементов или методе конечных объемов объект, который нужно проанализировать, делится на малые области в качестве исходного условия. Таким образом, дискретизированное основное уравнение выводится на предположении, что используются значения, определяющие геометрическую форму каждой малой области, то есть Вершина и Связность. В отличие от этого дискретизированное основное уравнение, используемое в настоящем изобретении, выводится из отличного и полностью нового образа мышления по сравнению с известным уровнем техники.

Тогда настоящее изобретение отличается применением дискретизированного основного уравнения, выведенного из такого нового образа мышления. Таким образом, в отличие от традиционного способа численного анализа способ в соответствии с настоящим изобретением решает традиционные проблемы вне зависимости от геометрической формы и предоставляет различные виды примечательных результатов.

Здесь ниже объясняется тот факт, что объем разделенной области и характеристическое значение граничной поверхности являются значениями, не требующими Вершины и Связности, которые определяют конкретную геометрическую форму разделенной области. Здесь значения, не требующие Вершины и Связности, указывают значения, которые можно задать без использования Вершины и Связности.

Например, когда рассматривается объем разделенной области, множественные вероятности присутствуют для геометрической формы разделенной области, чей объем принимает заранее установленное значение. То есть геометрическая форма разделенной области, чей объем принимает заранее установленное значение, может быть кубом или сферой. Затем, например, при ограничении, что полная сумма всех разделенных областей совпадает с объемом всей области анализа, объемы разделенных областей могут быть заданы путем вычисления с оптимизацией, выполненного, например, так, что объем каждой разделенной области должен быть как можно пропорциональнее кубу среднего расстояния от каждой соседней разделенной области. Таким образом, объем разделенной области можно признать в качестве величины, не требующей конкретной геометрической формы разделенной области (величины, не требующей Вершины и Связности).

Дополнительно характеристическое значение граничной поверхности может быть, например, площадью граничной поверхности, вектором нормали к граничной поверхности или контурной длиной граничной поверхности. Однако для геометрической формы разделенной области (то есть геометрической формы граничной поверхности) существуют многочисленные возможности, где характеристическое значение граничной поверхности имеет заранее установленное значение. Тогда, например, при ограничении, что длина среднего взвешенного вектора площади вектора нормали становится нулем для всех граничных поверхностей, окружающих разделенные области, характеристическое значение граничной поверхности может быть задано путем вычисления с оптимизацией, выполненного так, что направление вектора нормали к граничной поверхности становится ближе к отрезку прямой, который соединяет контрольные точки двух соседних разделенных областей (см. фиг. 5), и что полная сумма общих площадей граничных поверхностей разделенной области должна быть как можно пропорциональнее третьей-второй степени объема разделенной области. Таким образом, характеристическое значение граничной поверхности можно признать в качестве величины, не требующей конкретной геометрической формы разделенной области (величины, не требующей Вершины и Связности).

Дополнительно в настоящем изобретении описание, что "область анализа, разделенная на множество разделенных областей, не ограниченных формой прямоугольной сетки" указывает, что, по меньшей мере, одна из множества разделенных областей, составляющих область анализа, не имеет форму прямоугольной сетки. То есть обозначение указывает, что область анализа содержит разделенную область, имеющую форму, отличную от формы прямоугольной сетки.

Дополнительно в настоящем изобретении обозначение, что "используются только значения, не требующие Вершины и Связности", указывает, что значения, которые нужно подставить в дискретизированное основное уравнение, являются только значениями, не требующими Вершины и Связности.

Далее, со ссылкой на концептуальную схему фиг. 3, ниже приводится более подробное описание для примечательных результатов настоящего изобретения с помощью подхода сравнения предварительного процесса и решающего процесса в способе численного анализа, использующем настоящее изобретение, и в традиционном способе численного анализа.

В случае способа численного анализа, использующего настоящее изобретение, как показано на фиг. 3, в решающем процессе (этап вычисления физических значений в настоящем изобретении) физические значения в разделенных областях вычисляются с использованием дискретизированного основного уравнения, которое использует только значения, не требующие Вершины и Связности. Таким образом, в момент решения дискретизированного основного уравнения модель расчетных данных, сформированная в предварительном процессе, не должна содержать Вершину и Связность.

Затем, когда используется настоящее изобретение, объем разделенной области и характеристическое значение граничной поверхности используются в качестве значений, не требующих Вершины и Связности. Таким образом, модель расчетных данных, сформированная в предварительном процессе, не содержит Вершину и Связность, а содержит объем разделенной области, характеристическое значение граничной поверхности и другие вспомогательные данные (например, информацию о связи разделенных областей и координаты контрольных точек, которые описываются позже).

По существу, когда используется настоящее изобретение, как описано выше, физические значения в каждой разделенной области могут вычисляться на основе объема разделенной области и вышеупомянутого характеристического значения граничной поверхности, то есть на основе значений, не требующих геометрической формы разделенной области. Таким образом, физические значения могут вычисляться в состоянии, когда модель расчетных данных не содержит геометрическую форму разделенной области, то есть Вершину и Связность. Таким образом, когда используется настоящее изобретение, в предварительном процессе достаточно, чтобы формировалась модель расчетных данных, которая содержит, по меньшей мере, объем разделенной области и характеристическое значение граничной поверхности (площадь граничной поверхности и вектор нормали к граничной поверхности). Таким образом, физические значения могут вычисляться без формирования модели расчетных данных, содержащей Вершину и Связность.

Модель расчетных данных, не содержащая Вершину и Связность, не требует геометрической формы разделенной области и поэтому может формироваться без ограничения, вызванного геометрической формой разделенной области.

Таким образом, также значительно смягчается ограничение на коррекционную работу для данных о трехмерной форме. Таким образом, модель расчетных данных, не содержащая Вершину и Связность, можно сформировать гораздо проще модели расчетных данных, содержащей Вершину и Связность. Таким образом, в соответствии с настоящим изобретением снижается рабочая загрузка при формировании модели расчетных данных.

Дополнительно, даже когда используется настоящее изобретение, в предварительном процессе могут использоваться Вершина и Связность. То есть в предварительном процессе объем разделенной области, характеристики граничной поверхности и т.п. могут вычисляться с использованием Вершины и Связности. Даже в таком случае в решающем процессе физические значения могут вычисляться при условии, что доступен объем разделенной области и характеристики граничной поверхности. Таким образом, даже в случае, когда Вершина и Связность используются в предварительном процессе, можно избежать ограничения на геометрическую форму разделенной области, например ограничения, вызванного деформацией, кручением или т.п. разделенной области. Это снижает рабочую загрузку при формировании модели расчетных данных.

Дополнительно, когда используется настоящее изобретение, в предварительном процессе отменяется ограничение на геометрическую форму разделенной области. Таким образом, разделенная область может переходить в произвольную форму. Таким образом, область анализа можно легко подогнать под фактическую область, которую нужно проанализировать, без увеличения количества разделенных областей. Таким образом, точность анализа можно повысить без увеличения вычислительной нагрузки.

Дополнительно, когда используется настоящее изобретение, плотность распределения разделенных областей также может произвольно меняться. Таким образом, точность анализа также можно дополнительно повысить, позволяя при этом увеличение вычислительной нагрузки до необходимой степени.

Дополнительно, когда используется настоящее изобретение, в отличие от традиционного способа численного анализа, в решающем процессе вычисление объема разделенной области и характеристического значения граничной поверхности не должно использовать Вершину и Связность. Таким образом, вычислительную нагрузку в решающем процессе также можно снизить.

Дополнительно в настоящем изобретении, когда форма области анализа не меняется, перемещение разделенных областей не нужно. Таким образом, не нужны алгоритмы ближнего соседа, которые должны выполняться в каждый момент изменения времени в методе частиц. Соответственно, вычислительная нагрузка является небольшой. Дополнительно, как подробно описано позже, когда используется настоящее изобретение, в отличие от метода частиц физические значения могут вычисляться в состоянии, когда выполняются законы сохранения физических значений.

С другой стороны, в методе конечных объемов, который является традиционным способом численного анализа, предварительный процесс формирует модель расчетных данных, содержащую Вершину и Связность, выражающие геометрическую форму разделенной области. Тогда решающий процесс вычисляет объем разделенной области и характеристическое значение граничной поверхности (площадь граничной поверхности и вектор нормали к граничной поверхности) с использованием Вершины и Связности, содержащихся в модели расчетных данных, а затем вычисляет физические значения в каждой разделенной области. В этом случае необходимо, чтобы ограничение на геометрическую форму, то есть на отношение между Вершиной и Связностью, не вызывало проблему. Таким образом, модель расчетных данных (то есть сетку) нужно формировать в рамках ограничения, например деформации и кручения разделенной области. Это порождает проблему огромной ручной работы при формировании модели расчетных данных, как описано выше.

Дополнительно, также в методе конечных элементов решающий процесс вычисляет физические значения с использованием Вершины и Связности, содержащихся в модели расчетных данных. Таким образом, предварительный процесс должен формировать модель расчетных данных, содержащую Вершину и Связность, выражающие геометрическую форму разделенной области. Таким образом, появляется огромная ручная работа при формировании модели расчетных данных.

Дополнительно в методе вокселей, который является традиционным способом численного анализа, как показано на фиг. 3, в момент вычисления физических значений в решающем процессе Вершина и Связность не нужны. Однако форма разделенной области ограничивается вокселем. Таким образом, как описано выше, возникает проблема, что граница с внешней областью имеет ступенчатую форму. Соответственно, как описано выше, когда необходима достаточная точность анализа, количество вокселей увеличивается, и также увеличивается вычислительная нагрузка в решающем процессе. Это порождает проблему. Кроме того, в методе вокселей с коррекцией границы Вершина в конечном счете используется в момент вычисления объема и т.п. разделенной области. Таким образом, на формирование модели расчетных данных влияет геометрическая форма разделенной области.

Дополнительно в методе частиц, который является традиционным способом численного анализа, отсутствует понятие разделенной области. Таким образом, как показано на фиг. 3, в момент вычисления физических значений в решающем процессе Вершина и Связность не нужны. Однако перемещение частиц, которые задают модель расчетных данных, вместо разделенных областей вызывает увеличение вычислительной нагрузки, как описано выше. Дополнительно в методе частиц вычисление физических значений в состоянии, когда выполняется закон сохранения, является сложным.

Далее со ссылкой на фиг. 4 приводится сравнение между настоящим изобретением и традиционным методом конечных объемов с дополнительными подробностями.

В традиционном методе конечных объемов, который описан выше, предварительный процесс формирует модель расчетных данных, содержащую Вершину и Связность, которые определяют геометрическую форму разделенной области, полученную путем разделения сетки. Дополнительно, обычно решающий процесс требует информации о связи (в дальнейшем называемой ссылкой) для разделенной области. Таким образом, предварительный процесс формирует модель расчетных данных, содержащую Вершину, Связность и ссылку.

Тогда в традиционном методе конечных объемов, как показано на фиг. 4, модель расчетных данных, содержащая Вершину, Связность, ссылку и граничное условие, начальное условие и т.п., необходимые в решающем процессе, передаются из предварительного процесса в решающий процесс. Затем решающий процесс решает дискретизированное основное уравнение с использованием Вершины, Связности и т.п., содержащихся в переданной модели расчетных данных, и посредством этого вычисляет физические значения.

С другой стороны, в настоящем изобретении предварительный процесс формирует модель расчетных данных, содержащую объем каждой разделенной области, размещенной произвольно, характеристическое значение граничной поверхности (площадь граничной поверхности и вектор нормали к граничной поверхности) и ссылку. Дополнительно, как подробно описано позже, в настоящем изобретении в некоторых случаях, при необходимости, модель расчетных данных снабжается координатами контрольной точки, размещенной внутри каждой разделенной области.

Затем в настоящем изобретении, как показано на фиг. 4, модель расчетных данных, содержащая объем разделенной области, характеристическое значение граничной поверхности и ссылку (координаты контрольной точки, при необходимости), граничное условие, начальное условие и т.п. передаются из предварительного процесса в решающий процесс. Решающий процесс решает дискретизированное основное уравнение, используя объем разделенной области, характеристическое значение граничной поверхности и т.п., содержащиеся в переданной модели расчетных данных, и посредством этого вычисляет физические значения.

Затем, как видно из фиг. 4, существенное отличие настоящего изобретения от традиционного метода конечных объемов состоит в том, что решающий процесс вычисляет физические значения без использования Вершины и Связности. Этот момент является исключительным признаком настоящего изобретения. Этот признак следует из того, что решающий процесс использует дискретизированное основное уравнение, которое использует только значения, не требующие Вершины и Связности.

В результате, как показано на фиг. 4, в настоящем изобретении Вершину и Связность не нужно передавать в решающий процесс. Таким образом, достаточно, чтобы предварительный процесс формировал модель расчетных данных, не содержащую Вершину и Связность. Таким образом, по сравнению с традиционным методом конечных объемов, в настоящем изобретении можно гораздо проще сформировать модель расчетных данных. Соответственно, снижается рабочая загрузка при формировании модели расчетных данных.

Дополнительно, в некоторых случаях форма области анализа, на которой нужно выполнить численный анализ, меняется последовательно во времени, то есть область анализа включает в себя подвижную границу. В таком случае разделенные области нужно двигать и деформировать в соответствии с подвижной границей.

В традиционном методе конечных объемов вычисление физических значений в случае, в котором включается подвижная граница, достигается с помощью способа, в котором Вершина при каждом перемещении подвижной границы сохраняется заранее, или, в качестве альтернативы, с помощью способа, в котором разделение областей повторно выполняется, когда исчислимость утрачена из-за чрезмерной деформации разделенной области. В отличие от этого в настоящем изобретении вычисление физических значений в случае, в котором включается подвижная граница, достигается с помощью способа, в котором объем разделенной области, характеристики граничной поверхности и т.п. вместо Вершины вычисляются и сохраняются заранее, или, в качестве альтернативы, с помощью способа, в котором повторно выполняется разделение областей.

В традиционном методе конечных объемов или, в качестве альтернативы, в настоящем изобретении в случае, когда выбирается какой угодно из вышеупомянутых способов, нужно формировать множество моделей расчетных данных. Тем не менее, в традиционном методе конечных объемов в ситуации, когда формирование всего лишь одной модели расчетных данных требует огромного объема работ, формирование множества моделей во многих случаях становится недостижимым в диапазоне практически доступного объема работ.

С другой стороны, в настоящем изобретении модель расчетных данных не должна содержать Вершину и Связность, и согласованность Вершины и Связности не нужно учитываться при обработке с разделением областей. Таким образом, модель расчетных данных можно вычислять с весьма высокой скоростью. Соответственно, физические значения легко вычисляются в случае, где включается подвижная граница.

Здесь ниже приводится дополнительное описание для вышеупомянутой ссылки. Ссылка является информацией, описывающей отношение между разделенными областями, в которых физические значения меняются друг с другом. Тогда разделенные области, чье отношение описывается в этой ссылке, не должны пространственно прилегать друг к другу. То есть они могут пространственно отстоять друг от друга. Такая ссылка не имеет отношение к Вершине или Связности. Таким образом, по сравнению с Вершиной и Связностью ссылка может формироваться за весьм