Способ определения максимального размера и концентрации субмикронных аэрозольных частиц

Способ определения максимального размера и концентрации субмикронных аэрозольных частиц

Иллюстрации

Показать все

Реферат

Изобретение относится к области контрольно-измерительной техники, в частности к способам измерения характеристик аэрозольных частиц оптическими методами, и предназначено для определения максимального размера и концентрации субмикронных частиц в различных аэрозольных образованиях. Изобретение может найти применение в химической технологии, коллоидной химии, при разработке систем распыливания жидкости в различных отраслях техники, для контроля загрязнения окружающей среды.

Известны способы определения размеров и концентрации аэрозольных частиц, основанные на измерении ослабления параллельного пучка оптического зондирующего излучения [1-3]. При этом спектральный коэффициент пропускания зондирующего излучения измеряют для ограниченного набора длин волн, привлекают априорную информацию о спектре размеров аэрозольных частиц и проводят измерения дополнительных параметров (в частности, массовых расходов частиц и газа [1]). В качестве теоретической основы известных методов используют уравнение спектральной прозрачности (закон Бугера) для полидисперсных аэрозольных систем [4, 5] и теорию Ми для расчета факторов эффективности ослабления одиночных частиц [6].

Наиболее близким по технической сущности является способ определения дисперсности и концентрации частиц в аэрозольном облаке [7], основанный на измерении ослабления параллельного пучка зондирующего оптического излучения в диапазоне длин волн λ=(0.3÷1.1) мкм.

Недостатком данного способа является необходимость проведения дополнительных измерений оптической длины пути и объема аэрозольного облака с использованием двухракурсной видеосъемки. Проведение этих измерений вносит дополнительную погрешность и усложняет схему экспериментальной установки. При диагностике аэрозольных частиц субмикронных размеров применимость метода спектральной прозрачности связана с необходимостью измерения спектральных коэффициентов пропускания в ультрафиолетовой области спектра (λ<0.1 мкм) с высокой точностью для обеспечения возможности решения соответствующей обратной задачи оптики аэрозолей [5].

Техническим результатом изобретения является повышение точности определения характеристик субмикронных аэрозольных частиц без привлечения дополнительных измерений других параметров.

Технический результат изобретения достигается тем, что разработан способ определения максимального размера и концентрации субмикронных аэрозольных частиц, основанный на измерении ослабления параллельного пучка зондирующего оптического излучения. Спектральный коэффициент пропускания измеряют в диапазоне длин волн λ=λ_min÷λ_max и строят график функции

.

Из этого графика определяют координаты λ_∗, точки выхода функции т(Х) на асимптоту , максимальный диаметр D_max и массовую концентрацию C_m аэрозольных частиц определяют по формулам

,

,

где λ - длина волны зондирующего излучения, мкм;

τ(λ)=lnT^-1 (λ) - спектральная оптическая плотность;

T(λ)=J(λ)/J₀(λ) - измеренная зависимость спектрального коэффициента пропускания от длины волны зондирующего излучения;

J(λ), J₀(λ) - интенсивность прошедшего через аэрозольную систему и поступающего на нее зондирующего излучения, Вт;

D_max - максимальный диаметр аэрозольных частиц, мкм;

C_m - массовая концентрация аэрозольных частиц, кг/м³;

ρ - плотность материала аэрозольных частиц, кг/м³;

l - оптическая длина пути, м;

λ_∗, - координаты точки выхода на асимптоту функции , мкм;

α_∗(λ) - зависимость от длины волны значения параметра дифракции α=πD/λ, соответствующего абсциссе точки начала отклонения функции

Q(α) от функции Q_p(α);

D - диаметр аэрозольных частиц;

Q(α) - фактор эффективности ослабления, рассчитанный по точным формулам теории Ми для заданных зависимостей показателя преломления n(λ) и показателя поглощения æ(λ) материала аэрозольных частиц;

Q_p(α)=α·F(λ) - фактор эффективности ослабления для релеевского рассеяния,

функцию F(λ) рассчитывают по формуле

,

а границы диапазона длин волн зондирующего излучения λ_min, λ_max выбирают в видимой и ближней инфракрасной областях спектра с учетом известных зависимостей n(λ) и æ(λ) в этом диапазоне.

Полученный положительный эффект изобретения связан с тем, что одновременно определяются массовая концентрация частиц и их максимальный диаметр в исследуемой аэрозольной среде без проведения дополнительных исследований других параметров.

Рассмотрим обоснование заявляемого способа.

Определение массовой концентрации частиц

При прохождении монохроматического излучения с длиной волны λ через слой толщиной l, состоящий из равномерно распределенных монодисперсных частиц диаметром D с массовой концентрацией C_m происходит его ослабление за счет рассеяния и поглощения частицами. Количественной характеристикой ослабления является спектральный коэффициент пропускания

,

где J(λ) - поток излучения, прошедший сквозь слой; J₀(λ) - поток излучения, поступающий на слой.

Величина Т(λ) определяется законом Бугера [5]

,

где τ(λ) - спектральная оптическая плотность слоя.

Выражение для спектральной оптической плотности записывается в виде [5]

τ ( λ ) = 1.5 C m l ρ D Q ( α , m ) ,                                                                                                                               ( 1 ) ,

где ρ - плотность материала частиц;

Q(α, m) - безразмерный фактор эффективности ослабления, который зависит от параметра дифракции (параметра Ми) α=πD/λ и комплексного показателя преломления материала частицы m=n-iæ (n - показатель преломления; æ - показатель поглощения; ).

Значения n и æ в общем случае зависят от длины волны излучения λ. Зависимость Q(a, m) от параметра дифракции носит сложный колебательный характер и рассчитывается по точным формулам теории Ми [6].

Для случая «малых» частиц при выполнении условия релеевского рассеяния (α<1) [6] фактор эффективности ослабления определяется аналитической формулой [5]:

Q p = ( α , m ) = α ⋅ F ( λ ) ,                                                                                         ( 2 )

где .

Подставляя (2) в выражение для оптической плотности (1), получим:

τ ( λ ) = 1.5 С m l ρ D ⋅ F ( λ ) π D λ = 1.5 C m l ρ λ ⋅ F ( λ ) .                                                               ( 3 )

Из (3) следует, что в случае релеевского рассеяния величина оптической плотности τ(λ) не зависит от размера частиц D. Следовательно, по измеренным значениям τ(λ) из (3) можно определить массовую концентрацию частиц:

C m = ρ λ τ ( λ ) 1.5 π l F ( λ ) .                                                                                                 ( 4 )

Данный способ определения C_m по формуле (4) с использованием измеренного значения τ(λ) является корректным только в ограниченном диапазоне длин волн зондирующего излучения λ≥λ_* (λ_* - длина волны, ограничивающая область релеевского рассеяния). Для определения λ_* измеряют спектральную оптическую плотность в некотором диапазоне длин волн λ_min≤λ≤λ_max и строят график зависимости

,

где τ(λ) - измеренная зависимость спектральной оптической плотности от длины волны излучения.

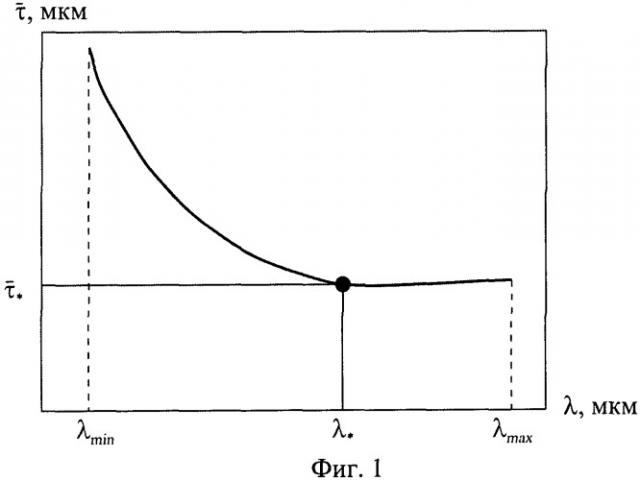
График функции τ(λ) имеет два участка (фиг.1):

1. τ ¯ ( λ ) монотонно убывает при λ<λ_*.

2. τ ¯ ( λ ) = τ ¯ ∗ = c o n s t при λ≥λ_*.

Для диапазона длин волн λ>λ_* массовая концентрация частиц определяется по формуле (4).

Покажем, что данный способ определения массовой концентрации частиц применим и для полидисперсных частиц, если для всех частиц выполняется условие релеевского рассеяния. В случае полидисперсных частиц выражение для спектральной оптической плотности имеет вид [5]:

τ ( λ ) = 1.5 C m l ρ ⋅ ∫ 0 ∞ Q ( α , m ) D 2 f ( D ) d D ∫ 0 ∞ D 3 f ( D ) d D ,                                                                             ( 6 )

где f(D) - функция счетного распределения частиц по размерам.

Подставляя в (6) выражение (2) для Q_p(α, m) в случае релеевского рассеяния, получим формулу, полностью совпадающую с формулой (4) для определения массовой концентрации частиц.

Определение максимального размера частиц

Как было отмечено выше, фактор эффективности ослабления зависит от двух параметров - параметра дифракции а и æ комплексного показателя преломления материала частиц m=n-iæ. Значения n и зависят в общем случае от длины волны излучения λ, причем для разных материалов эти зависимости носят разный характер.

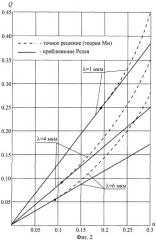
В случае релеевского рассеяния зависимость фактора эффективности ослабления от параметра дифракции линейна в соответствии с уравнением (2). Зависимость фактора эффективности ослабления от параметра дифракции, рассчитанного по точным формулам теории Ми, совпадает с релеевской до некоторого граничного значения α_*, а при α>α_* отклоняется от нее: Q(α, m)>Q_p(α, m). При этом значение α_* зависит от длины волны излучения (фиг.2), что связано с дисперсией m (зависимость n и æ от λ).

Таким образом, для известных зависимостей n(λ) и æ(λ) в диапазоне λ_min≤λ≤λ_mаx можно построить графики Q(α, m) и Q_p(α, m), проводя расчеты факторов эффективности ослабления по точным формулам теории Ми и по уравнению (2) для релеевского рассеяния. Из этих графиков (фиг.2) определяется зависимость от длины волны значения параметра дифракции, соответствующего абсциссе точки начала отклонения функции Q(α, m) от Q_p(α, m):

α * ( λ ) = π D λ .

Подставляя в эту зависимость значение λ_*, определенное выше как абсцисса точки выхода на асимптоту τ ¯ ( λ ) , получим формулу для определения максимального диаметра аэрозольных частиц:

D m a x = λ * π α * ( λ * ) .                                                                                             ( 7 )

Сущность изобретения поясняется следующими рисунками:

Фиг.1 - график функции τ ¯ ( λ ) для определения координат λ_*, τ ¯ * точки выхода этой зависимости на асимптоту τ ¯ ( λ ) = c o n s t .

Фиг.2 - зависимость факторов эффективности ослабления от параметра дифракции для частиц сажистого углерода.

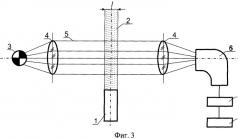
Фиг.3 - схема лабораторной установки для измерения характеристик аэрозольных частиц.

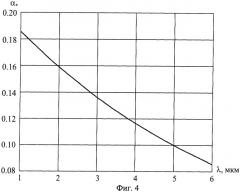
Фиг.4 - зависимость от длины волны значения параметра дифракции, соответствующего абсциссе точки начала отклонения функции Q(α) от Q_p(α) для частиц сажистого углерода.

Пример реализации способа

На фиг.3 приведена схема лабораторной установки для измерения характеристик частиц сажистого углерода в пламени газовой горелки. Поток продуктов сгорания 2 газовой горелки через цилиндрическую трубку 1 заданного диаметра l поступал в зону измерений. Параллельный пучок зондирующего излучения 5 с начальной интенсивностью J₀(λ) от источника сплошного спектра 3, в качестве которого использовалась лампа СИ-10-300 с ленточным вольфрамовым излучателем, создавался оптической фокусирующей системой 4. Прошедший через аэрозольную систему ослабленный поток излучения J(λ) поступал на вход спектрально-аналитического комплекса 6, 7.

Обработка экспериментальных данных по зависимости спектрального коэффициента пропускания от длины волны зондирующего излучения Т(λ) проводилась с помощью персонального компьютера 8.

Предварительно проводился расчет факторов эффективности ослабления Q(a,m) по точным формулам теории Ми и по формуле (2) для релеевского рассеяния. Примеры расчетных графиков приведены на фиг.2. При проведении расчетов использовались зависимости n(λ) и æ(λ) для частиц сажистого углерода, приведены в [8] для диапазона λ=(1÷6) мкм:

n(λ)=1.6+0.3λ,

æ(λ)=λ^0.6,

где [λ]=мкм.

Обработка графиков Q(α, m) и Q_p(α, n) для диапазона длин волн λ=(1÷6) мкм позволили получить зависимость α_*(λ) для частиц сажистого углерода, приведенную на фиг.4. Эта зависимость аппроксимировалась формулой (погрешность аппроксимации не более 3%):

α * = 0.22 ⋅ exp ( − 0.16 ⋅ λ ) ,                                                                       ( 8 )

где [λ]=мкм.

Результаты измерений показали, что значение длины волны, соответствующее выходу на асимптоту функции τ ¯ ( λ ) , составляло λ_*=2 мкм. Соответствующее значение α_*, определенное по уравнению (8), составило α_*=0.16 мкм. Максимальный диаметр частиц сажистого углерода

D max = λ * π α * ( λ * ) = 2 ⋅ 0.16 π = 0.1   м к м ,

что хорошо согласуется с известными литературными данными [8]. Значение массовой концентрации частиц сажистого углерода (ρ=1.75 г/см³) изменялось в широких пределах C_m=(2÷15) мг/см³ в зависимости от коэффициента избытка окислителя газовой смеси, поступающей в горелку.

По результатам примера видно, что заявленный способ позволяет одновременно определять массовую концентрацию и максимальный диаметр аэрозольных частиц с высокой точностью без проведения дополнительных измерений других параметров. Высокая точность определения C_m и D_max связана со строгой обоснованностью границ применимости релеевского рассеяния.

ЛИТЕРАТУРА

1. Пат. РФ 717628, МПК G01N 15/02. Способ измерения среднего радиуса металлических капель в двухфазных потоках / Е.В.Соловьев. - №2343588/18-25; заявл. 01.04.1976; опубл. 25.02.1980, Бюл. №7.

2. Пат. РФ 1420474, МПК G01N 15/02. Способ определения параметров частиц аэрозоля в газовом потоке / Г.И.Левашенко, В.И.Анцулевич, С.Л.Шуралев, С.В.Симоньков. - №4037554/24-25; заявл. 17.03.1986; опубл. 30.08.1988, Бюл. №32.

3. Пат. РФ 2335760, МПК G01N 15/02. Оптический способ определения размеров частиц дисперсной фазы / О.Л.Власова, О.А.Писарев, А.Г.Безрукова, П.В.Плотникова. - №2006121402/28; заявл. 13.06.2006; опубл. 10.10.2008, Бюл. №28.

4. Дейрменджан Д. Рассеяние электромагнитного излучения сферическими полидисперсными частицами. - М.: Мир, 1971. - 165 с.

5. Архипов В.А. Лазерные методы диагностики гетерогенных потоков. - Томск: Изд-во Том. ун-та, 1987. - 140 с.

6. Хюлст Ван де Г. Рассеяние света малыми частицами. - М.: ИЛ, 1961. - 536 с.

7. Пат. РФ 2441218, МПК G01N 15/02. Способ определения дисперсности и концентрации частиц в аэрозольном облаке / В.А.Архипов, А.А. Павленко, С.С.Титов, О.Б.Кудряшова, С.С.Бондарчук. - №2010143653/28; заявл. 25.10.2010; опубл. 27.01.2012, Бюл. №3.

8. Блох А.Г. Теплообмен в топках паровых котлов. - Л.: Энергоатомиздат, 1984. - 240 с.

Способ определения максимального размера и концентрации субмикронных аэрозольных частиц, основанный на измерении ослабления параллельного пучка зондирующего оптического излучения, отличающийся тем, что спектральный коэффициент пропускания измеряют в диапазоне длин волн λ=λ_min÷λ_max, строят график функции ,из которого определяют координаты λ_∗, точки выхода этой функции на асимптоту , максимальный диаметр D_max и массовую концентрацию C_m аэрозольных частиц определяют по формулам , ,где λ - длина волны зондирующего излучения, мкм;τ(λ)=lnT^-1 (λ) - спектральная оптическая плотность;T(λ)=J(λ)/J₀(λ) - измеренная зависимость спектрального коэффициента пропускания от длины волны зондирующего излучения;J(λ), J₀(λ) - интенсивность прошедшего через аэрозольную систему и поступающего на нее зондирующего излучения, Вт;D_max - максимальный диаметр аэрозольных частиц, мкм;C_m - массовая концентрация аэрозольных частиц, кг/м³;ρ - плотность материала аэрозольных частиц, кг/м³;l - оптическая длина пути, м;λ_∗, - координаты точки выхода на асимптоту функции , мкм;α_∗(λ) - зависимость от длины волны значения параметра дифракции α=πD/λ, соответствующего абсциссе точки начала отклонения функцииQ(α) от функции Q_p(α);D - диаметр аэрозольных частиц;Q(α) - фактор эффективности ослабления, рассчитанный по точным формулам теории Ми для заданных зависимостей показателя преломления n(λ) и показателя поглощения æ(λ) материала аэрозольных частиц;Q_p(α)=α·F(λ) - фактор эффективности ослабления для релеевского рассеяния,функцию F(λ) рассчитывают по формуле ,а границы диапазона длин волн зондирующего излучения λ_min, λ_max выбирают в видимой и ближней инфракрасной областях спектра с учетом известных зависимостей n(λ) и æ(λ) в этом диапазоне.