Поляризационно-фазовый способ измерения угла крена подвижного объекта и радионавигационная система для его реализации

Поляризационно-фазовый способ измерения угла крена подвижного объекта и радионавигационная система для его реализации

Иллюстрации

Показать все

Реферат

Изобретение относится к радионавигации и может использоваться, например, в пилотажно-навигационных системах ориентации летательного аппарата (ЛА) при заходе на посадку по приборам.

Известные способы и устройства измерения угла крена подвижного объекта основаны на использовании инерциальных систем навигации, в частности гироскопических систем ориентации [1-4]. Применительно к ЛА таким инерциальным системам навигации присущ ряд недостатков. Во-первых, с течением времени происходит постоянное накапливание ошибки измерений и за один час полета она составляет величину единицы градусов [2, 3]. Во-вторых, если ЛА развивает значительные перегрузки, то происходит увеличение собственной скорости прецессии гироскопа, что в ряде случаев может привести к полной потере его работоспособности [2].

Поскольку известные инерциальные средства измерения угла крена подвижного объекта основаны на другом физическом принципе, по сравнению с заявляемым, то они не могут рассматриваться в качестве аналогов, так как не имеют общих признаков.

Известны способ измерения пеленга подвижного объекта и устройство для его реализации (патент SU №1251003, М. кл.⁴ G01S, 3/02, приоритет от 29.01.85) [5].

Способ измерения пеленга подвижного объекта заключается в том, что из двух точек с известными координатами, расположенных в плоскости измерений на расстоянии d друг от друга, одновременно излучают ортогонально поляризованные электромагнитные волны с равными амплитудами, фазами и длинами волн. На подвижном объекте одновременно принимают ортогонально поляризованные электромагнитные волны и измеряют разность фаз Δφ между ними, после чего определяют пеленг β подвижного объекта относительно нормали к середине базы d, соединяющей точки излучений электромагнитных волн, по формуле:

β = arcsin ( λ 2 π d ⋅ Δ ϕ ) ,                                      ( 1 )

где λ - длина волны излучаемых ортогонально поляризованных электромагнитных волн.

Недостатком этого способа является ограниченные функциональные возможности, заключающиеся в измерении только одного навигационного элемента - пеленга подвижного объекта, и невозможно измерить его угол крена.

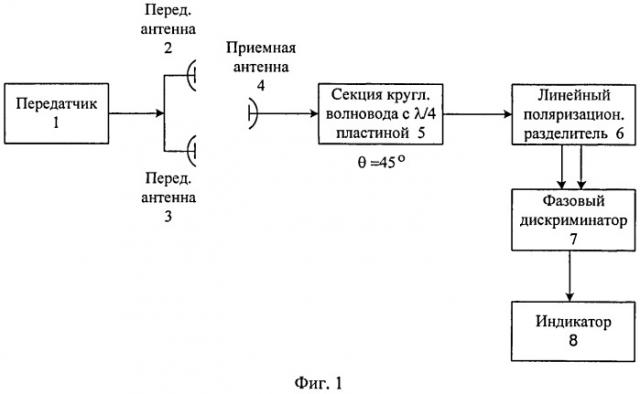
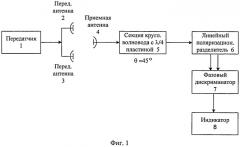
Устройство для измерения пеленга подвижного объекта содержит передатчик с подключенными к нему двумя передающими антеннами с ортогональными линейными поляризациями, расположенными в точках с известными координатами в плоскости измерений на расстоянии d друг от друга и расположенных на подвижном объекте, приемную всеполяризованную антенну, линейный поляризационный разделитель, амплитудно-фазовый дискриминатор и вычислитель. При этом вход линейного поляризационного разделителя подключен к выходу приемной всеполяризованной антенны, два его выхода подключены к двум входам амплитудно-фазового дискриминатора, а его выход подключен к входу вычислителя. Причем линейный поляризационный разделитель ориентирован так, что его орты собственной системы координат совпадают с осями плеч ортогонально расположенных по отношению друг к другу прямоугольных волноводов и составляют угол 45° с плоскостью измерений. Работа устройства заключается в том, что передатчик через подключенные к нему две передающие антенны излучает ортогонально линейно поляризованные электромагнитные волны. На подвижном объекте суммарная электромагнитная волна принимается всеполяризованной антенной и затем поступает на вход линейного поляризационного разделителя, выполненного в виде волновода круглого сечения с переходом на два ортогонально расположенных волновода прямоугольного сечения. Выбранная ориентация линейного поляризационного разделителя позволяет осуществить прием суммарной электромагнитной волны в линейном ортогональном поляризационном базисе, единичные орты которого совпадают с ортами собственной системы координат линейного поляризационного разделителя, ориентированными под углом 45° к плоскости измерений. Таким образом в линейном поляризационном разделителе происходит разделение поступающей на его вход со стороны круглого волновода суммарной электромагнитной волны на две линейные ортогональные по поляризации электромагнитные волны, после чего выходные сигналы линейного поляризационного разделителя со стороны прямоугольных волноводов поступают на входы амплитудно-фазового дискриминатора, где происходит измерение амплитуд ортогонально линейно поляризованных сигналов, формируется их отношение и по найденному отношению измеряется разность фаз Δφ и в соответствии с формулой (1) рассчитывается вычислителем пеленг подвижного объекта.

Недостатком этого устройства является ограниченные функциональные возможности, обусловленные тем, что измеряется только пеленг подвижного объекта и невозможно измерить его угол крена.

Наиболее близким по совокупности признаков к заявляемому поляризационно-фазовому способу измерения угла крена подвижного объекта и радионавигационной системе для его реализации является навигационная система для измерения пеленга подвижного объекта, реализующая поляризационно-амплитудный способ измерения (авт.св. №1355955, М. кл.⁴ G01S, 3/02, приоритет от 9.12.85) [6], в которой устраняется влияние угла крена подвижного объекта на точность измерения его пеленга.

Суть поляризационно-амплитудного способа измерения пеленга подвижного объекта заключается в том, что из двух точек с известными координатами, расположенных в плоскости измерений на расстоянии d друг от друга, одновременно излучают ортогонально линейно поляризованные электромагнитные волны с равными амплитудами, фазами и длинами волн. Тогда суммарная электромагнитная волна может быть представлена в векторной форме в исправлении β, с учетом (1), в виде [6]:

E → ˙ Σ = [ 1 0 ] + [ 0 1 ] ⋅ e j Δ ϕ = [ 1 e j Δ ϕ ] ,                                     ( 2 )

где [ 1 0 ] - вектор Джонса горизонтально линейно поляризованной излучаемой электромагнитной волны, представленный в линейном ортогональном поляризационном базисе и совпадающий с осью ОХ неподвижной опорной прямоугольной системы координат YOX;

[ 0 1 ] - вектор Джонса вертикально линейно поляризованной излучаемой электромагнитной волны, представленный в линейном ортогональном поляризационном базисе и совпадающий с осью OY неподвижной опорной прямоугольной системы координат YOX;

Δ ϕ = 2 π d λ sin β - фазовый сдвиг между излучаемыми ортогонально линейно поляризованными электромагнитными волнами в точке приема в направлении β;

[ 1 e j Δ ϕ ] - вектор Джонса суммарной электромагнитной волны, представленный в линейном ортогональном поляризационном базисе, единичные орты которого совпадают с горизонтальной плоскостью и перпендикуляром к этой плоскости соответственно.

На борту подвижного объекта принимают суммарную электромагнитную волну (2) в собственном синфазном круговом поляризационном базисе, единичные орты которого соответствуют волнам с левой и правой круговой поляризациями, электрические векторы которых в начальный момент времени t=0 совпадают с вектором напряженности электрического поля излучаемой горизонтально линейно поляризованной электромагнитной волны, разделяют принятую суммарную электромагнитную волну (2) на две ортогонально поляризованные по кругу составляющие левого E ˙ → L и правого E → ˙ R направления вращения вектора напряженности электрического поля, измеряют их амплитуды E_L и E_R соответственно и рассчитывают пеленг подвижного объекта по формуле [6]:

β = arcsin [ 2 a r c t g E L E R ⋅ λ 2 π d ] .                                         ( 3 )

Отмечается [6], что отношение амплитуд E L E R , равное:

E L E R = 1 − cos Δ ϕ 1 + cos Δ ϕ = | t g Δ ϕ 2 | ,                                            ( 4 )

не зависит от угла крена подвижного объекта и зависит только от разности фаз Δφ между излучаемыми ортогонально линейно поляризованными электромагнитными волнами в точке приема на подвижном объекте.

Недостатком данного поляризационно-амплитудного способа измерения является ограниченные функциональные возможности, заключающиеся в том, что измеряется только один навигационный элемент - пеленг подвижного объекта - и невозможно измерить его угол крена.

Навигационная система для измерения пеленга подвижного объекта [6] содержит передатчик с подключенными к нему двумя передающими антеннами с ортогональными собственными линейными поляризациями и расположенными в точках с известными координатами в плоскости измерений на расстоянии d друг от друга и расположенные на подвижном объекте приемную всеполяризованную антенну, секцию круглого волновода с встроенной четвертьволновой фазовой пластиной, линейный поляризационный разделитель, амплитудный дискриминатор и вычислитель, при этом вход секции круглого волновода с встроенной четвертьволновой фазовой пластиной соединен с выходом приемной всеполяризованной антенны, а выход секции подключен к входу линейного поляризационного разделителя со стороны круглого волновода, а два его выхода со стороны прямоугольных волноводов подключены к соответствующим двум входам амплитудного дискриминатора, а его выход подключен к входу вычислителя, причем четвертьволновая фазовая пластина ориентирована под углом 45° к широкой стенке прямоугольного волновода одного из плеч линейного поляризационного разделителя.

Работа навигационной системы заключается в следующем.

Передатчик, через подключенные к нему две передающие антенны с ортогональными собственными линейными поляризациями, излучает ортогонально линейно поляризованные электромагнитные волны с равными амплитудами, фазами и длинами волн. На подвижном объекте суммарная электромагнитная волна (2) принимается всеполяризованной приемной антенной и поступает на последовательно соединенные секцию круглого волновода со встроенной четвертьволновой фазовой пластиной и линейный поляризационный разделитель, выполненный в виде круглого волновода с переходом на два ортогонально расположенных по отношению друг к другу прямоугольных волноводов. Сочетание секции круглого волновода со встроенной четвертьволновой фазовой пластиной и линейного поляризационного разделителя позволяет разделить поступающую на вход суммарную электромагнитную волну (2) на две ортогонально поляризованные по кругу волны с левым E → L и правым E → R направлением вращения вектора электрического поля, после чего сигналы с выходов плеч линейного поляризационного разделителя поступают на соответствующие входы амплитудного дискриминатора, на выходе которого формируется напряжение, равное отношению амплитуд E_L/E_R в виде (4). Затем вычислитель, по найденному отношению (4) в соответствии с (3), рассчитывает пеленг подвижного объекта.

К недостаткам данной навигационной системы [6] относятся ограниченные функциональные возможности, проявляющиеся в том, что измеряется только пеленг подвижного объекта и невозможно измерить его угол крена.

Поляризационно-фазовый способ измерения угла крена подвижного объекта заключается в том, что из двух точек с известными координатами, расположенных в плоскости измерений на расстоянии d друг от друга, одновременно излучают ортогонально линейно поляризованные электромагнитные волны с равными амплитудами, фазами и длинами волн, на борту подвижного объекта принимают суммарную электромагнитную волну в собственном круговом ортогональном поляризационном базисе, единичные орты которого соответствуют волнам с правой и левой круговой поляризациями, разделяют принятую суммарную электромагнитную волну на две ортогонально поляризованные по кругу составляющие правого E → R и левого E → L направления вращения вектора напряженности электрического поля, отличается от прототипа тем, что измеряют разность фаз между ними Δφ_RL=φ_R-φ_L и по измеренной разности фаз Δφ_RL рассчитывают угол крена γ между поперечной осью подвижного объекта и горизонтальной плоскостью, при этом точки излучения электромагнитных волн находятся в горизонтальной плоскости, излучаемые электромагнитные волны имеют линейные горизонтальную и вертикальную ориентации плоскости поляризации, совпадающие с горизонтальной плоскостью и перпендикуляром к этой плоскости соответственно, а прием суммарной электромагнитной волны осуществляется в собственном несинфазном круговом поляризационном базисе, в котором единичные орты соответствуют волнам с левой и правой круговой поляризациями, электрические векторы которых в начальный момент времени t=0 совпадают с горизонтальной и вертикальной ориентацией плоскости поляризации излучаемых электромагнитных волн и совпадают также с поперечной и вертикальной осями подвижного объекта соответственно, при этом абсолютные временные фазы волн между правой и левой круговыми поляризациями, образующими единичные орты кругового поляризационного базиса, отличаются на величину 90°.

Установим связь разности фаз Δφ_RL между ортогонально поляризованными по кругу составляющими правого E → R и левого E → L направления вращения вектора напряженности электрического поля с углом крена γ подвижного объекта, используя известный формализм векторов и матриц Джонса [7, 8]. Очевидно, чтобы установить искомую связь, необходимо представить суммарную электромагнитную волну E → ˙ Σ , заданную своими проекциями в линейном ортогональном поляризационном базисе в виде (2), в круговом ортогональном поляризационном базисе как линейную суперпозицию в виде:

E → ˙ Σ = E ˙ L e → ˙ L + E ˙ R e → ˙ R ,                                      ( 5 )

где базисные векторы e → ˙ L и e → ˙ R определяются как [7, 8]

e → ˙ L = 1 2 [ 1 − j ] и e → ˙ R = 1 2 [ 1 j ] ,                     ( 6 )

и соответствуют единичным волнам с левой и правой круговой поляризациями, заданными своими проекциями в линейном ортогональном поляризационном базисе.

Тогда суммарная электромагнитная волна E → ˙ Σ с произвольным состоянием поляризации, заданная своими проекциями в линейном ортогональном поляризационном базисе в виде (2), может быть определена на борту подвижного объекта, имеющего, в общем случае, крен ±γ, при переходе в круговой несинфазный ортогональный поляризационный базис, опустив временную зависимость сигналов, на входе приемника в виде:

E → ˙ R L = [ E ˙ L E ˙ R ] = 1 2 [ 1 j j 1 ] [ cos γ ± sin γ ∓ sin γ cos γ ] ⋅ E → ˙ Σ ,                               ( 7 )

где E → ˙ Σ = 1 2 [ 1 e j Δ ϕ ] - нормированный, для удобства, вектор Джонса суммарной электромагнитной волны, заданный своими проекциями в линейном ортогональном поляризационном базисе, единичные орты [ e ˙ → x , e ˙ → y ] которого совпадают с осями ОХ и OY прямоугольной системы координат YOX;

[ cos γ ± sin γ ∓ sin γ cos γ ] - оператор поворота на произвольный угол крена ±γ,

1 2 [ 1 j j 1 ] - оператор перехода из линейного ортогонального поляризационного базиса в круговой несинфазный ортогональный поляризационный базис [9], в котором в начальный момент времени t=0 абсолютные временные фазы волн правой и левой круговых поляризаций, образующих единичные орты кругового поляризационного базиса (6), отличаются на величину 90°.

Подставляя в (7) значения +γ и осуществив необходимые матричные вычисления, получим аналитические выражения для ортогонально поляризованных по кругу составляющих левого E ˙ L и правого E ˙ R направления вращения на входе приемника в виде:

E ˙ L = 1 2 [ ( cos γ − sin ( Δ ϕ − γ ) ) + j ( cos ( Δ ϕ − γ ) − sin γ ) ]                          ( 8 )

и

E ˙ R = 1 2 [ ( cos ( Δ ϕ + γ ) − sin γ ) + j ( cos γ + sin ( Δ ϕ + γ ) ) ] .                        ( 9 )

Используя известные соотношения [9], амплитуды A_L и A_R, а также фазы φ_L и φ_R сигналов (8) и (9) имеют вид:

A L = 2 2 1 − sin Δ ϕ ,           ( 10 ) и ϕ L = a r c t g cos ( Δ ϕ − γ ) − sin γ cos γ − sin ( Δ ϕ − γ ) ,            ( 11 )

A R = 2 2 1 + sin Δ ϕ ,           ( 12 ) и ϕ R = a r c t g cos γ + sin ( Δ ϕ + γ ) cos ( Δ ϕ + γ ) − sin γ ,              ( 13 )

Соответственно отношение амплитуд A_L/A_R и разность фаз Δφ_RL ортогонально поляризованных по кругу составляющих E ˙ L и E ˙ R после преобразований для положительных углов крена +γ имеют вид:

A L A R = 1 − sin Δ ϕ 1 + sin Δ ϕ = | t g ( 45 ∘ − Δ ϕ 2 ) | ,                            ( 14 )

Δ ϕ R L = ϕ R − ϕ L = 2 γ ,                                                 ( 15 )

откуда следует, что:

γ [ г р а д . ] = Δ ϕ R L 2 [ г р а д . ] .                                             ( 16 )

Аналогично, подставляя в (7) значения -γ, получим аналитические выражения для ортогонально поляризованных по кругу составляющих левого E ˙ L и правого E ˙ R направления вращения на входе приемника в виде:

E ˙ L = 1 2 [ ( cos γ − sin ( γ + Δ ϕ ) ) + j ( sin γ + cos ( γ + Δ ϕ ) ) ] ,                           ( 17 )

E ˙ R = 1 2 [ ( sin γ + cos ( Δ ϕ − γ ) ) + j ( cos γ + sin ( Δ ϕ − γ ) ) ] .                              ( 18 )

Соответственно амплитуды A_L и A_R, а также фазы φ_L и φ_R сигналов (17) и (18) имеют вид:

A L = 2 2 1 − sin Δ ϕ ,         ( 19 ) и ϕ L = a r c t g sin γ + cos ( γ + Δ ϕ ) cos γ − sin ( γ + Δ ϕ ) ,               ( 20 )

A R = 2 2 1 + sin Δ ϕ ,          ( 21 ) и ϕ R = a r c t g cos γ + sin ( Δ ϕ − γ ) sin γ + cos ( Δ ϕ − γ ) ,                 ( 22 )

Выполнив необходимые преобразования, отношение амплитуд A_L/A_R и разность фаз Δφ_RL=φ_R-φ_L ортогонально поляризованных по кругу составляющих E ˙ L и E ˙ R для отрицательных углов крена -γ имеют вид:

A L A R = 1 − sin Δ ϕ 1 + sin Δ ϕ = | t g ( 45 ∘ − Δ ϕ 2 ) | ,                                ( 23 )

и

Δ ϕ R L = ϕ R − ϕ L = − 2 γ ,                                      ( 24 )

откуда следует, что

γ [ г р а д . ] = − Δ ϕ R L 2 [ г р а д . ] .                                 ( 25 )

Из анализа (14) и (23) следует, что отношение амплитуд A_L/A_R ортогонально поляризованных по кругу составляющих E ˙ L и E ˙ R зависит только от разности фаз Δφ между излучаемыми ортогонально линейно поляризованными электромагнитными волнами в точке приема на подвижном объекте, т.е. зависит только от угловых координат подвижного объекта и не зависит от угла крена γ подвижного объекта. В то же время из анализа (15) и (24) видно, что разность фаз Δφ_RL между ортогонально поляризованными по кругу составляющими E ˙ R и E ˙ L , наоборот, определяется только углом крена γ подвижного объекта и не зависит от его угловых координат. Сравнивая (16) и (25), окончательно имеем выражение для определения угла крена γ подвижного объекта в виде:

γ [ г р а д . ] = ± Δ ϕ R L 2 [ г р а д . ] ,                                    ( 26 )

где «+» - соответствует положительному углу крена γ, когда правая, по ходу движения, поперечная ось подвижного объекта находится ниже горизонтальной плоскости,

«-» - соответствует отрицательному углу крена γ, когда правая, по ходу движения, поперечная ось подвижного объекта находится выше горизонтальной плоскости,

Δφ_RL=φ_R-φ_L - разность фаз между ортогонально поляризованными по кругу составляющими правого E ˙ R и левого E ˙ L направления вращения на входе приемника [град.].

В случае, если из двух точек, расположенных в горизонтальной плоскости на расстоянии d друг от друга, излучать в равносигнальном направлении, совпадающем с перпендикуляром к середине базы d, соединяющей эти точки, ортогонально линейно поляризованные электромагнитные волны с равными амплитудами и длинами волн, но с начальной разностью фаз Δφ₀=90°, то соотношения (14) и (23) преобразуются к виду:

A L A R = 1 − cos Δ ϕ 1 + cos Δ ϕ = | t g Δ ϕ 2 | ,                                       ( 27 )

что полностью согласуется с выражением (4), полученным в прототипе [6].

Таким образом, проводя сравнительный анализ полученных выражений (15) и (24), видим, что при появлении крена подвижного объекта одновременно возникает фазовый сдвиг между ортогонально поляризованными по кругу составляющими E ˙ R и E ˙ L суммарной электромагнитной волны E ˙ Σ , принятой на подвижном объекте в круговом поляризационном базисе, обусловленный, в общем случае, изменением угла ориентации эллипса поляризации (или плоскости поляризации) принятой суммарной электромагнитной волны. Последнее определяет физическую основу определения крена подвижного объекта по измеренной разности фаз Δφ_RL между ортогонально поляризованными по кругу составляющими E ˙ R и E ˙ L .

Использование заявляемой совокупности признаков для измерения угла крена подвижного объе