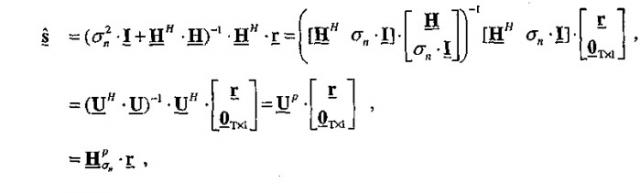Эффективный расчет весовых коэффициентов фильтра для системы mimo

Эффективный расчет весовых коэффициентов фильтра для системы mimo

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Изобретение, в общем, относится к области связи и, более конкретно, к методикам расчета весовых коэффициентов фильтров в системе связи.

Уровень техники

В системе связи с множеством входов и множеством выходов (MIMO, МВМВ) для передачи данных используется множество (T) передающих антенн передающей станции и множество (R) приемных антенн приемной станции. Канал MIMO, формируемый T передающими антеннами и R приемными антеннами, может быть разложен на S пространственных каналов, где S≤min {T, R}. S пространственных каналов можно использовать для передачи данных таким образом, чтобы достичь большей общей пропускной способности и/или более высокой надежности.

Передающая станция может одновременно передавать T потоков данных через T передающих антенн. В этих потоках данных возникают искажения в соответствии с откликом канала MIMO, и их качество дополнительно ухудшается в результате воздействия шумов и взаимных помех. Приемная станция принимает передаваемые потоки данных через R приемных антенн. Принимаемый сигнал от каждой приемной антенны содержит масштабированную версию T потоков данных, переданных передающей станцией. Переданные потоки данных, таким образом, диспергированы среди R сигналов, принятых через R приемных антенн. Приемная станция затем выполняет пространственную обработку приемника для R принятых сигналов, используя матрицу пространственного фильтра, для восстановления переданных потоков данных.

Определение весовых коэффициентов матрицы пространственного фильтра требует объемной обработки. Это связано с тем, что матрицу пространственного фильтра обычно получают на основе функции, которая содержит обращение матрицы, и прямые расчеты обращения матрицы требуют объемных вычислений.

Таким образом, в данной области техники требуется разработка методики для эффективного расчета весовых коэффициентов фильтра.

Сущность изобретения

Здесь описаны методики эффективного расчета весовых коэффициентов матрицы пространственного фильтра. Эти методики позволяют исключить непосредственный расчет обращения матрицы.

В первом варианте воплощения для получения матрицы М пространственного фильтра Эрмитову матрицу P итерационно получают на основе матрицы H отклика канала, и обращение матрицы опосредованно рассчитывают путем итерационного получения Эрмитовой матрицы. Эрмитова матрица может быть инициализирована до единичной матрицы. Одну итерацию затем выполняют для каждой строки матрицы отклика канала, и эффективную последовательность расчетов выполняют для каждой итерации. Для i-й итерации получают промежуточный вектор a _i строки на основе вектора h _i отклика канала, который представляет собой i-ю строку матрицы отклика канала. Скалярное значение r _i получают на основе промежуточного вектора строки и вектора строки отклика канала. Промежуточную матрицу C _i также получают на основе промежуточного вектора строки. Эрмитову матрицу затем обновляют на основе скалярного значения и промежуточной матрицы. После окончания всех итераций, получают матрицу пространственного фильтра на основе Эрмитовой матрицы и матрицы отклика канала.

Во втором варианте воплощения выполняют множество поворотов для итерационного получения первый матрицы P ^1/2 и второй матрицы B для псевдообращенной матрицы отклика канала. Одну итерацию выполняют для каждой строки матрицы отклика канала. Для каждой итерации формируют матрицу Y, содержащую первую и вторую матрицы из предыдущей итерации. Множество поворотов Гивенса затем выполняют для матрицы Y для обнуления элементов в первой строке матрицы, для получения обновленных первой и второй матриц для следующей итерации. После того как все итерации будут закончены, получают матрицу пространственного фильтра на основе первой и второй матриц.

В третьем варианте воплощения формируют матрицу X на основе матрицы отклика канала и разлагают (например, с использованием разложения по собственным значениям), для получения унитарной матрицы V и диагональной матрицы Λ. Разложение может быть получено в результате итерационного выполнения поворотов Якоби для матрицы X. Матрицу пространственного фильтра затем получают на основе унитарной матрицы, диагональной матрицы и матрицы отклика канала.

Различные аспекты и варианты выполнения изобретения более подробно описаны ниже.

Краткое описание чертежей

Свойства и сущность настоящего изобретения будут более понятны из подробного описания, приведенного ниже, которое следует рассматривать совместно с чертежами, на которых одинаковыми номерами ссылочных позиций обозначены соответствующие элементы на всех чертежах.

На фиг.1, 2 и 3 представлены процессы, выполняемые для расчета матрицы пространственного фильтра MMSE (МСКО, минимальная среднеквадратическая ошибка), на основе первого, второго и третьего вариантов воплощения, соответственно.

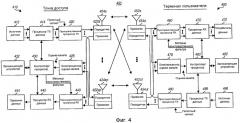
На фиг.4 показана блок-схема точки доступа и терминала пользователя.

Подробное описание изобретения

Слово "примерный", используемое здесь, означает "используемый в качестве примера, случая или иллюстрации". Любой вариант выполнения или конструкция, описанный здесь как "примерный", необязательно следует рассматривать как предпочтительный или преимущественный по сравнению с другими вариантами выполнения или конструкциями.

Описанные здесь методики расчета весовых коэффициентов фильтра можно использовать для системы MIMO с одной несущей и системы MIMO с множеством несущих. Множество несущих могут быть получены с использованием мультиплексирования с ортогональным частотным разделением сигналов (OFDM), при множественном доступе с разделением частот с перемежением (IFDMA), локализованном множественном доступе с разделением частот (LFDMA), или некоторой другой методики модуляции. OFDM, IFDMA и LFDMA эффективно разделяют общую полосу пропускания системы на множество (K) ортогональных частотных подполос, которые также называются тонами, поднесущими, элементами сигнала и частотными каналами. Каждую подполосу ассоциируют с соответствующей поднесущей, которая может быть модулирована данными. В системе OFDM символы модуляции передают в области частот для всех или поднабора K подполос. В IFDMA передают символы модуляции в области времени по подполосам, которые равномерно распределены по K подполосам. В LFDMA передают символы модуляции в области времени и обычно в соседних подполосах. Для ясности большая часть следующего описания направлена на систему MIMO с одной несущей, в которой используется одна поднесущая.

Канал MIMO, сформированный множеством (T) передающих антенн в передающей станции и множеством ® приемных антенн в приемной станции, может характеризоваться матрицей H отклика канала размером RxT, которая может быть задана как:

Уравнение (1)

где h_i,j , для i=1,...,R и j=1,...,T обозначает усиление связи или комплексное усиление канала между передающей антенной j и приемной антенной i; и

h _i представляет собой вектор строки отклика канала размером 1×T для приемной антенны i, который представляет собой i-ю строку матрицы H.

Для простоты в следующем описании предполагается, что канал MIMO имеет полный ранг и, что количество пространственных каналов (S) задается как: S=T≤R.

Передающая станция может передавать T символов модуляции одновременно через T передающих антенн в каждый период символа. Передающая станция может выполнять или может не выполнять пространственную обработку для символов модуляции перед передачей. Для простоты в следующем описании предполагается, что каждый символ модуляции передают через передающую антенну без какой-либо пространственной обработки.

Приемная станция получает R принятых символов из R приемных антенн в каждый период символа. Принятые символы могут быть выражены как:

Уравнение (2)

где s представляет собой вектор размером T×1, в котором T символов модуляции переданы передающей станцией;

r представляет собой вектор размером R×1, где R принимаемых символов получают в приемной станции через R приемных антенн; и

n представляет собой вектор шумов размером R×1.

Для простоты можно предположить, что шумы представляют собой аддитивный белый Гауссов шум (AWGN) с нулевым средним вектором и матрицей ковариации δ² _n×I, где δ² _n представляет собой дисперсию шума и I представляет собой единичную матрицу.

В приемной станции могут использоваться различные методики пространственной обработки для восстановления символов модуляции, переданных передающей станцией. Например, приемная станция может выполнять пространственную обработку приемника с минимальной среднеквадратичной ошибкой (MMSE), следующим образом:

Уравнение (3)

где M представляет собой матрицу пространственного фильтра MMSE размером T×R;

P представляет собой Эрмитову матрицу ковариации размером T×T для ошибки оценки s-;

представляет собой вектор размером T×1, который представляет собой оценку s; и

" ^H " обозначает сопряженную перестановку.

Матрица P ковариации может быть задана как P=E[(s-)×(s-)^H], где E[] представляет собой операцию математического ожидания. P также представляет собой Эрмитову матрицу, недиагональные элементы которой имеют следующие свойства p_i,j=p*_i,j, где "*" обозначает комплексно сопряженное число.

Как показано в уравнении (3), матрица М пространственного фильтра MMSE имеет расчет обращенной матрицы. Прямой расчет обращения матрицы требует выполнения большого объема компьютерных операций. Матрица пространственного фильтра MMSE может быть более эффективно получена на основе вариантов выполнения, описанных ниже, которые позволяют опосредованно рассчитывать обращение матрицы с использованием итеративного процесса, вместо непосредственного расчета обращения матрицы.

В первом варианте воплощения расчета матрицы М пространственного фильтра MMSE рассчитывают Эрмитову матрицу P на основе уравнении Риккати. Эрмитова матрица P может быть выражена следующим образом:

Уравнение (4)

Эрмитова матрица P _i размером TxT может быть определена как:

Уравнение (5)

Лемма обращения матрицы может быть применена к уравнению (5) для получения следующего:

Уравнение (6)

где r _i представляет собой скалярную действительную величину. Уравнение (6) называется уравнением Риккати. Матрица P _i может быть инициализирована как P ₀=•I. После выполнения R итераций уравнения (6), для i=1,...,R, получают матрицу P _R как матрицу P, или P=P _R.

Уравнение (6) может быть перемножено на определенные коэффициенты для получения следующего:

Уравнение (7)

где матрицу P _i инициализируют как P ₀=I, и матрицу P получают как P=•P _R. Уравнения (6) и (7) отличаются от решения уравнения (5). Для простоты использовали те же переменные P _i и r_i для обоих уравнений (6) и (7), даже, несмотря на то, что эти переменные имеют разные значения в двух уравнениях. Конечные результаты, полученные по уравнениям (6) и (7), то есть, P _R для уравнения (6) и •P _R для уравнения (7), эквивалентны. Однако расчеты для первой итерации уравнения (7) упрощаются, благодаря использованию P ₀ в качестве единичной матрицы.

Каждая итерация уравнения (7) может быть выполнена следующим образом:

Уравнение (8a)

Уравнение (8b)

Уравнение (8c)

Уравнение (8d)

где a _i представляет собой вектор промежуточной строки размером 1×T элементов с комплексным значением; и

C представляет собой промежуточную Эрмитову матрицу размером T×T.

В системе (8) уравнений последовательность операций структурирована для эффективного расчета с помощью аппаратных средств. Скалярное значение r_i рассчитывают перед матрицей C _i. Разделение по r_i в уравнении (7) достигается с помощью обращения и умножения. Обращение r_i может быть выполнено параллельно с расчетом C _i. Обращение r_i достигается со сдвигом для нормализации r_i и с применением справочной таблицы для получения обращенного значения r_i. Нормализация r_i может быть компенсирована умножением на C _i.

Матрицу P _i инициализируют как Эрмитову матрицу или P ₀=I, и она остается Эрмитовой матрицей во всех следующих итерациях. Следовательно, только верхнюю (или нижнюю) диагональную матрицу требуется рассчитывать для каждой итерации. После окончания R итераций получают матрицу P, как P=•P _R. Матрица пространственного фильтра MMSE может затем быть рассчитана следующим образом:

Уравнение (9)

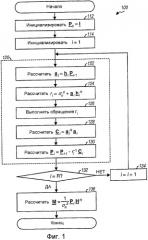
На фиг.1 показан процесс 100 расчета матрицы M пространственного фильтра MMSE, основанной на первом варианте воплощения. Матрица P _i инициализирована как P ₀=1 (блок 112), и индекс i используется для обозначения номера итерации, инициализируется как i=1 (блок 114). Затем выполняют R итераций уравнения Риккати.

Каждую итерацию уравнения Риккати выполняют с помощью блока 120. Для i-й итерации вектор a _i промежуточной строки рассчитывают на основе заявленного вектора h _i отклика канала и Эрмитовой матрицы P _i+1 предшествующей итерации, как показано в уравнении (8a) (блок 122). Скалярное значение r_i рассчитывают на основе дисперсии δ ² _n шумов, вектора a _i промежуточной строки и вектора h _i строки отклика канала, как показано в уравнении (8b) (блок 124). Скалярная величина r _i после этого становится обращенной (блок 126). Промежуточную матрицу C _i рассчитывают на основе a _i промежуточной строки, как показано в уравнении (8c) (блок 128). Матрицу P _i затем обновляют на основе инвертированной скалярной величины r _i и промежуточной матрицы C _i, как показано в уравнении (8d) (блок 130).

Затем определяют, были ли выполнены все R итераций (блок 132). В случае отрицательного ответа, выполняют последовательное приращение индекса i (блок 134), и процесс возвращается к блоку 122 для выполнения другой итерации. В противном случае, если все R итераций были выполнены, рассчитывают матрицу М пространственного фильтра MMSE на основе Эрмитовой матрицы P _R для последней итерации, матрицы H отклика каналов и дисперсии δ ² _n шумов, как показано в уравнении (9) (блок 136). Матрицу М затем можно использовать для пространственной обработки приемника, как показано в уравнении (3).

Во втором варианте воплощения расчета матрицы М пространственного фильтра MMSE определяют Эрмитову матрицу P путем получения квадратного корня P, который представляет собой P ^1/2, на основе итерационной процедуры. Пространственная обработка приемника в уравнении (3) может быть выражена следующим образом:

Уравнение (10)

где U= представляет собой дополненную матрицу канала размером (R+T)×T;

U ^p представляет собой псевдообращенную матрицу размером T×(R+T), полученную в результате операции обращения или псевдообращения Мура-Пенроуза для U, или U ^p=(U ^H ∙ U)^-1 ∙ U ^H;

0 _Tx1 представляет собой вектор размером T×1, содержащий одни нули; и

H ^p _δn представляет собой подматрицу размером T×R, содержащую первые R столбцов U ^p.

Разложение QR может быть выполнено для матрицы с дополненным каналом следующим образом:

Уравнение (11)

где Q представляет собой матрицу размером (R+T)×T с ортонормированными столбцами;

R представляет собой матрицу размером T×T, которая не является единичной матрицей;

B представляет собой матрицу размером R×T, содержащую первые R строк матрицы Q; и

Q ₂ представляет собой матрицу размером T×T, содержащую последние T строк матрицы Q.

QR (КО, квазиобращенное) разложение в уравнении (11) разлагает матрицу дополненного канала на ортогональную матрицу Q и на не единичную матрицу R. Ортогональная матрица Q имеет следующее свойство: Q ^H•Q=I, что означает, что столбцы ортогональной матрицы являются ортогональными относительно друг друга, и каждый столбец имеет единичную степень. Не единичная матрица представляет собой матрицу, для которой может быть рассчитана обращенная матрица.

Эрмитова матрица P может быть затем выражена как:

Уравнение (12)

R представляет собой разложение Колецкого или квадратный корень матрицы P^-1. Следовательно, P ^1/2 равно R ^-1 и называется квадратным корнем матрицы P.

Псевдообращенная матрица в уравнении (10) затем может быть выражена как:

Уравнение (13)

Подматрица H ^P _δn, которая также представляет собой матрицу пространственного фильтра MMSE, затем может быть выражена как:

Уравнение (14)

Уравнение (10) затем может быть выражено как:

Уравнение (15)

Матрицы P ^1/2 и B могут быть рассчитаны итерационно следующим образом:

или Уравнение (16)

Уравнение (17)

где Y _i представляет собой матрицу размером (T+R+1)×(T+1), содержащую элементы, полученные на основе P ^1/2 _i-1, B _i-1 и h _i;

θ _i представляет собой унитарную матрицу преобразования размером (T+1)×(T+1);

Z _i представляет собой преобразованную матрицу размером (T+R+1)×(T+1), содержащую элементы для P_i ^1/2, B _i и r _i;

e _i представляет собой вектор размером R×1 с единицей (1,0) в качестве i-го элемента и с остальными нулевыми элементами; и

k _i представляет собой вектор размером T×1 и I _i представляет собой вектор R×1, причем оба они являются несущественными.

Матрицы P ^1/2 и B инициализируют как P ₀ ^1/2=•I и B ₀=0 _RxT.

Преобразование в уравнение (17) может быть выполнено итерационно, как описано ниже. Для ясности каждую итерацию уравнения (17) называют внешней итерацией. R внешних итераций уравнения (17) выполняют для R векторов h _i отклика канала для i=1,...,R. Для каждой внешней итерации унитарная матрица δ _i преобразования в уравнении (17) преобразуется в трансформированную матрицу Z _i, содержащую все нули в первой строке, за исключением первого элемента. Первый столбец преобразованной матрицы Z _i содержит r_i ^1/2, k _i и I _i. Последние T столбцов Z _i содержат обновленные P _i ^1/2 и B _i. Первый столбец Z _i не требуется рассчитывать, поскольку только P _i ^1/2 и B _i используются в следующей итерации. P _i ^1/2 представляет собой верхнюю треугольную матрицу. После окончания R внешних итераций получают P _R ^1/2 как P ^1/2, и B _R получают как B. Матрица М пространственного фильтра MMSE может быть затем рассчитана на основе P ^1/2 и B, как представлено в уравнении (14).

Для каждой внешней итерации i преобразование по уравнению (17) может выполняться путем последовательного обнуления одного элемента в первой строке Y _i одновременно с 2×2 поворотами Гивенса. T внутренних итераций поворота Гивенса могут быть выполнены для обнуления последних T элементов в первой строке Y _i.

Для каждой внешней итерации i, матрица Y _i,j может быть инициализирована как Y _i1=Yi. Для каждой внутренней итерации j для j=1,...,T, внешней итерации i, первоначально формируют подматрицу Y′_i,j размером (T+R+1)×2, содержащую первый и (j+1)-й столбцы Y _i,j. Затем выполняют поворот Гивенса для подматрицы Y′_i,j для генерирования подматрицы Y"_i,j размером (T+R+1)×2, содержащей ноль во втором элементе в первой строке. Поворот Гивенса может быть выражен как:

Уравнение (18)

где G _i,j представляет собой матрицу поворота Гивенса размером 2×2 для j-й внутренней итерации i-й внешней итерации, которая описана ниже. Матрицу Y _i,j+1 затем формируют вначале путем установки Y _i,j+1=Y _i,j, затем замены первого столбца Y _i,j+1 первым столбцом Y"_i,j и затем замены (j+1)-го столбца матрицы Y _i,j+1 вторым столбцом Y"_i,j. Поворот Гивенса, таким образом, модифицирует только два столбца Y _i,j j-й внутренней итерации для получения Y _i,j+1 для следующей внутренней итерации. Поворот Гивенса может быть выполнен на месте двух столбцов Y _i для каждой внутренней итерации, в результате чего промежуточные матрицы Y _i,j, Y′_i,j, Y"_i,j и Y _i,j+1 не нужны и описаны выше для ясности изложения.

Для j-й внутренней итерации i-й внешней итерации матрица G _i,j поворота Гивенса определяется на основе первого элемента (который всегда представляет собой действительную величину) и (j+1)-го элемента в первой строке матрицы Y _i,j. Первый элемент может быть обозначен как α, и (j+1)-й элемент может быть обозначен как b-e^jθ. Матрица G _i,j поворота Гивенса затем может быть получена следующим образом:

Уравнение (19)

где c= и s= для уравнения (19).

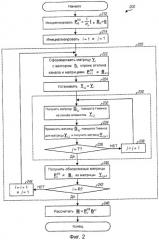
На фиг.2 показан процесс 200, предназначенный для расчета матрицы М пространственного фильтра MMSE на основе второго варианта воплощения. Матрицу P _i ^1/2 инициализируют как P₀ ^1/2=•I, и матрицу B _i инициализируют как B ₀=0 (блок 212). Индекс i для обозначения номера внешней итерации инициализируют как i=1, и индекс j, используемый для обозначения номера внутренней итерации, инициализируют как j=1 (блок 214). Затем выполняют R внешних итераций унитарного преобразования в соответствии с уравнением (17) (блок 220).

Для i-й внешней итерации вначале формируют матрицу Y _i с вектором h _i строки отклика канала и матрицы P _i-1 ^1/2 и B _i-1, как показано в уравнении (17) (блок 222). Матрица Y _i затем обозначается как матрица Y _i,j для внутренних итераций (блок 224). T внутренних итераций поворота Гивенса затем выполняют для матрицы Y _i,j (блоке 230).

Для j-й внутренней итерации получают матрицу G _i,j поворота Гивенса на основе первого и (j+1)-го элементов в первой строке Y _i,j, как показано в уравнении (19) (блок 232). Матрицу G _i,j поворота Гивенса затем применяют для первого и (j+1)-го столбцов Y _i,j для получения Y _i,j+1, как показано в уравнении (18) (блок 234). Затем определяют, были ли выполнены все T внутренние итерации (блок 236). Если ответ представляет собой "Нет", тогда индекс j увеличивают на единицу (блок 238), и обработка возвращается к блоку 232 для выполнения другой внутренней итерации.

Если все T внутренние итерации были выполнены для текущей внешней итерации, и ответ представляет собой "Да" для блока 236, тогда последняя Y _i,j+1 равна Z _i в уравнении (17). Обновленные матрицы P _i ^1/2 и B _i получают из последней Y _i,j+1 (блок 240). Затем определяют, были ли выполнены все R внешних итераций (блок 242). Если будет получен ответ "Нет", тогда индекс i увеличивают на единицу, и индекс j повторно инициализируют как j=1 (блок 244). Обработка затем возвращается в блок 222 для выполнения другой внешней итерации с P _i ^1/2 и B _i. В противном случае, если все R внешние итерации были выполнены, и ответ представляет собой "Да" для блока 242, тогда рассчитывают матрицу М пространственного фильтра MMSE, на основе P _i ^1/2 и B _i, как показано в уравнении (14) (блок 246). Матрицу М можно затем использовать для пространственной обработки приемника, как показано в уравнении (15).

В третьем варианте воплощения расчета матрицы М пространственного фильтра MMSE выполняют разложение по собственным значениям P ^-1 следующим образом:

Уравнение (20)

где V представляет собой унитарную матрицу T×T собственных векторов; и

Λ представляет собой диагональную матрицу размером T×T с действительными собственными значениями вдоль диагонали.

Разложение по собственным значениям Эрмитовой матрицы X _2x2 размером 2×2 может быть получено с использованием разных методик. В варианте воплощения разложение по собственным значениям X _2x2 получают путем выполнения сложного поворота Якоби для X _2x2, для получения матрицы V _2x2 размером 2×2 собственных векторов X _2x2. Элементы X _2x2 и V _2x2 могут быть заданы как:

Уравнение (21)

Элементы V _2x2 могут быть рассчитаны непосредственно из элементов X _2x2 следующим образом:

Уравнение (22a)

Уравнение (22b)

Уравнение (22c)

Уравнение (22d)

Уравнение (22e)

Уравнение (22f)

Уравнение(22g)

Уравнение (22h)

Уравнение (22i)

Уравнение (22j)

Уравнение (22k)

Разложение по собственным значениям Эрмитовой матрицы X размером T×T, которая больше чем 2×2, может быть выполнено в итеративном процессе. В таком итеративном процессе неоднократно используется поворот Якоби для обнуления недиагональных элементов в X. Для итеративного процесса индекс i обозначает номер итерации и инициализируется как i=1. X представляет собой Эрмитову матрицу размером T×T, которая должна быть разложена, и устанавливается как X=P ^-1. Матрица D _i представляет собой аппроксимацию диагональной матрицы Λ в уравнении (20) и инициализируется как D ₀=X. Матрица V представляет собой аппроксимацию унитарной матрицы V в уравнении (20) и инициализируется как V ₀=I.

Одиночная итерация поворота Якоби для обновления матриц D _i и V _i может быть выполнена следующим образом. Вначале Эрмитову матрицу D _pq размером 2×2 формируют на основе текущей матрицы D _i следующим образом:

Уравнение (23)

где d_p,q представляет собой элемент в местоположении (p,q) матрицы D _i, p{1,...,T}, g{1,...,T} и p≠q. D _pq представляет собой подматрицу D _i размером 2×2, и четыре элемента D_pq представляют собой четыре элемента в местоположениях (p, p), (p, q), (q, p) и (q, q) матрицы D _i. Индексы p и q могут быть выбраны, как описано ниже.

Затем выполняют разложение по собственным значениям D _pq, как показано в уравнении (22), для получения унитарной матрицы V _pq размером 2×2 собственных векторов D _pq. Для разложения по собственным значениям D _pq, X _2x2 в уравнении (21) заменяют на D _pq, и V _2x2 из уравнения (22j) или (22k) представляют как V _pq.

Матрица T_pq сложного поворота Якоби размером TxT затем формируется с V _pq, T _pq и представляет собой единичную матрицу с четырьмя элементами в местоположениях (p, p), (p, q), (q, p) и (q, q), которые заменены элементами v_1,1, v_1,2, v_2,1 и v_2,2, соответственно, в матрице Y _pq.

Матрица D _i затем обновляется следующим образом:

Уравнение (24)

Уравнение (24) обнуляет два недиагональных элемента в местоположениях (p, q) и (q, p) в матрице D _i. Расчет может изменять значения других недиагональных элементов в D _i.

Матрицу V _i также обновляют следующим образом:

Уравнение (25)

V _i можно рассматривать как матрицу кумулятивного преобразования, которая содержит все матрицы T _pq поворота Якоби, использовавшиеся для D _i.

Каждая итерация с поворотом Якоби обнуляет два недиагональных элемента матрицы Di. Множество итераций поворота Якоби могут быть выполнены для разных значений индексов p и q, для обнуления всех недиагональных элементов D _i. Один проход по всем возможным значениям индексов p и q может быть выполнен следующим образом. Индекс p последовательно изменяется от 1 до T-1 с приращением единица. Для каждого значения p индекс q последовательно изменяется от p+1 до T с приращением единица. Поворот Якоби выполняют для каждой разной комбинации значений p и q. Множество проходов могут быть выполнены до тех пор, пока D _i и V _i не станут представлять достаточно точные оценки Λ и V, соответственно.

Уравнение (20) может быть переписано следующим образом:

Уравнение (26)

где Λ ^-1 представляет собой диагональную матрицу, элементы которой представляют собой обращенные значения соответствующих элементов Λ. Разложение по собственным величинам X=P ^-1 представляет оценки Λ и V. Λ может быть инвертирована для получения Λ ^-1.

Матрица пространственного фильтра MMSE может быть затем рассчитана следующим образом:

Уравнение (27)

На фиг.3 представлен процесс 300, предназначенный для расчета матрицы М пространственного фильтра MMSE, на основе третьего варианта воплощения. Эрмитову матрицу P ^-1 первоначально получают на основе матрицы H отклика канала, как показано в уравнении (20) (блок 312). Затем выполняют разложение по собственным величинам P ^-1 для получения унитарной матрицы V и диагональной матрицы Λ, как также показано в уравнении (20) (блок 314). Разложение по собственным величинам может итерационно выполняться с множеством поворотов Якоби, как описано выше. Матрицу М пространственного фильтра MMSE затем получают на основе унитарной матрицы V, диагональной матрицы Λ и матрицы H отклика канала, как показано в уравнении (27) (блок 316).

Матрица М пространственного фильтра MMSE, полученная на основе каждого из описанных выше вариантов воплощения, представляет собой смещенное решение MMSE. Смещенную матрицу М пространственного фильтра можно масштабировать с помощью диагональной матрицы D _mmse для получения несмещенной матрицы MMSE M _mmse пространственного фильтра. Матрица D _mmse может быть получена как D_mmse=[diag[M•H]]^-1, где diag[М•H] представляет собой диагональную матрицу, содержащую диагональные элементы М•H.

Описанные выше расчеты также можно использовать для получения матриц пространственного фильтра для методики с обращением в нуль не значащих коэффициентов (ZF) (которая также называется методикой обращения матрицы с корреляцией канала (CCMI, ОМКК)), методики комбинирования максимального отношения (MRC, КМО) и так далее. Например, приемная станция может выполнять пространственную обработку приемника с обращением в нуль не значащих коэффициентов и MRC, следующим образом:

Уравнение (28)

Уравнение (29)

где M _zf представляет собой матрицу пространственного фильтра размером T×R с обращенными в ноль не значащими коэффициентами;

M _mrc представляет собой матрицу пространственного фильтра MRC с размером T×R;

P _zf=(H^H•H)^-1 представляет собой Эрмитову матрицу размером T×T; и

[diag(P _zf)] представляет собой диагональную матрицу размером T×T, содержащую диагональные элементы P _zf.

Обращение матрицы необходимо для непосредственного расчета P _zf. P _zf могут быть рассчитаны с использованием вариантов воплощения, описанных выше для матрицы пространственного фильтра MMSE.

В приведенном выше описании предполагается, что T символов модуляции передают одновременно через T передающие антенны, без какой-либо пространственной обработки. Передающая станция может выполнять пространственную обработку перед передачей следующим образом:

Уравнение (30)

где x представляет собой вектор размером T×1 с T символами передачи, которые должны быть переданы через T передающих антенн; и

W представляет собой матрицу передачи размером T×S. Матрица W передачи может представлять собой (1) матрицу с правыми единичными векторами, полученными путем выполнения разложения единичного значения H, (2) матрицу собственных векторов, полученную путем выполнения разложения по собственным величинам H ^H H, или (3) управляющую матрицу, выбранную для пространственного распределения символов модуляции по S пространственным каналам в канале MIMO. Матрица H _eff эффективного отклика канала, наблюдаемого по символам модуляции, затем может быть задана как H _eff = H•W. Описанная выше комбинация может выполняться на основе H _eff вместо H.

Для ясности приведенного выше описания, в нем приведена система MIMO с одной несущей, с одной подполосой. Для системы MIMO с множеством несущих матрица H(k) отклика канала может быть получена для каждой подполосы k, представляющей интерес. Матрица М(k) пространственного фильтра затем может быть получена для каждой подполосы k на основе матрицы H(k) отклика канала для этой подполосы.

Описанные выше расчеты для матрицы пространственного фильтра могут быть вы