Катушки гельмгольца-ишкова

Катушки гельмгольца-ишкова

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к электротехнике и может быть использовано для создания устройств с однородным магнитным полем, протяженность которого сравнима с радиусом возбуждающих обмоток. Технический результат состоит в повышении однородности магнитного поля и эффективности его создания. Устройство состоит из катушек Гельмгольца и внешнего магнитопровода. Катушки Гельмгольца типичные круглые. Внешний магнитопровод состоит из двух частей цилиндрической формы с цилиндрическими выемками для размещения катушек Гельмгольца и глухими торцовыми частями. Внешний магнитопровод уменьшает магнитное сопротивление внешней части магнитной цепи, благодаря чему повышается и уровень или однородность магнитного поля между его полосами.

Предлагаемое изобретение относится к области техники магнитных полей и может быть применено для создания эталонных магнитных полей заданного уровня однородности и величины.

Аналогом предлагаемого изобретения являются сами катушки Гельмгольца, которые представляют собой систему двух идентичных круглых катушек, которые размещены соосно на расстоянии радиуса катушек и включены согласно так, что образуются единые магнитные линии магнитного поля и величина магнитного поля на оси системы катушек между плоскостями катушек получается достаточно однородной.

Недостаток аналога состоит в ограниченности однородности поля и эффективности его создания. Для улучшения однородности магнитного поля в рабочей области применяют еще дополнительные пары катушек большого размера со встречным включением дополнительного поля. Это увеличивает габариты лабораторного оборудования и снижает эффективность энергетических затрат на питание, которое должно быть стабильным.

Прототипом предлагаемого изобретения является соленоид Ишкова по патенту RU 2364000. Он состоит из обмотки возбуждения прямоугольного сечения и вешнего магнитопровода в форме цилиндрической оболочки и двух торцевых фланцев, внутренние поверхности которых являются полюсами. Внутри соленоида между полюсами при пропускании электрического тока по обмотке возбуждения создается магнитное поле повышенной однородности.

Недостаток прототипа в свете поставленной цели предлагаемого изобретения состоит в том, что доступ во внутреннее пространство соленоида сопряжен с необходимостью демонтажа фланцев при аксиальном доступе в рабочее пространство соленоида. Особенно сложна проблема радиального доступа в рабочее пространство соленоида.

Техническим решением проблемы свободного доступа в область однородного магнитного поля по оси и радиусу является магнитопровод из двух цилиндрических половинок, из которых нижняя закреплена, а верхняя является съемной частью так, что при поднятой верхней части открывается доступ в рабочее пространство катушек Гельмгольца и по оси, и по радиусу. В качестве примера устройство показано на фиг.1.

Устройство состоит из катушек Гельмгольца 1 и внешнего магнитного провода цилиндрической формы 2, который сам состоит из верхней части 3 и нижней части 4. Торцы магниторовода 2 закреплены по радиусу катушек Гельмгольца 1. По периферии неявных полюсов 5 закреплены обмотки катушек Гельмгольца 1. Исследуемый объект 6 помещается в центральной части устройства. Конструктивно магнитопровод состоит из двух идентичных цилиндрических частей с цилиндрическими выемками для катушек Гельмгольца 1, которые стыкуются плоскими торцами. Отличие верхней подъемной части 3 состоит в наличии конической юбочки 7, которая сопрягается с коническим срезом 8 на нижней неподвижной части магнитопровода 4.

Подъем верхней части 3 и ее фиксация к нижней части 4 осуществляется известными способами.

Действует устройство следующим образом.

При поднятой верхней части 3 в центральную часть устройства помещается исследуемый объект 6, соединительные коммуникации с ним осуществляются через нижнюю часть 4 известными способами. При опускании верхней части 3 она однозначно фиксируется к нижней части 4 посредством конической юбочки 7 и конического среза 8.

При пропускании электрического тока по обмоткам катушек Гельмгольца 1 между полюсами 5 возникает необходимое магнитное поле 9. Величина магнитного поля определяется магнитодвижущей силой катушек, а однородность поля обеспечивается специфическим перераспределением структуры линий магнитного поля во внешнем магнитопроводе 2.

На фиг.2 представлен ход линий магнитного поля в предлагаемом изобретении. Самая длинная линия магнитного поля проходит в центральной части полюсов и имеет длину 2πR+2R(π+1).

Самая короткая линия поля проходит по периферии полюсов и имеет длину 2R, где R - радиус катушек Гельмгольца.

Для центральной линии магнитного поля отношение длин межполюсной части к магнитопроводной составляет величину 1 2 ( π + 1 ) ≃ 1 8 ,

для периферийной линии магнитного поля это отношение будет

R 2 R = 1 2 > 1 8 .

Из приведенных соотношений следует, что для центральных магнитных линий только восьмая часть проходит между полюсами, а для периферийных магнитных линий только половина. Следовательно, применение внешнего магнититопровода для катушек Гельмгольца деформирует линии магнитного поля так, что уменьшает магнитное сопротивление. Для центральных магнитных линий многократно, а для периферийных магнитных линий - лишь двукратно. Это существенно повысит однородность магнитного поля в предлагаемом изобретении и повысит его уровень при том же токе в катушках Гельмгольца.

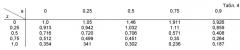
В Табл.1 представлена радиальная зависимость отношений длины магнитной линии в магнитопроводе к длине магнитной линии между полюсами магнитопровода l_F, которая определена по вышеприведенной методике. Для простоты записи принято R=1, а r - радиальное удлинение от центра полюсов. Это нелинейная зависимость.

Табл.1
r	0	0,2	0,4	0,6	0,8	1,0
ℓ F = 2 π ( 1 − r ) + 1 ℓ o = 1	7,28	6,024	4,768	3,512	2,256	1,0

Аналитический расчет магнитиных полей, создаваемых тонким проводником с током, основывается на законе Био-Савара-Лапласа, см. Савельев В.И. «Курс общей физики», т. 2, М., Наука, 1970 с.132.

d B → = μ o 4 π i d ℓ r 2 sin ( d ℓ →     ^ r ⇀ )

где µ_о=4·10^-7 _, Гн/м - магнитная постоянная;

i - сила электрического тока, А;

dl - элементарный участок с током I;

r ⇀ _- радиус-вектор из исследуемой точки к элементарному току;

d ℓ →     ^ r ⇀ - угол между элементарным током d ℓ → и радиус-вектором r ⇀ _, фиг.3.

Дифференциал магнитного поля в центре кругового тока на его оси,

где d B → = μ o 4 π ⋅ i d ℓ R 2

R - радиус кругового тока, м.

Величина магнитного поля в центре кругового тока определяется интегралом В = μ o 4 π i R 2   ∫ d ℓ = μ o 4 π ⋅ i R 2   ∫ o 2 π d φ = μ o 2 i R 2 [ Т л ] ,

где dl=Rdφ.

Вне плоскости витка магнитное поле имеет две компоненты, фиг.4. Аксиальная компонента магнитного поля зависит от угла β.

B_z=Bsinβ, где sinβ= β = R R 2 + z 2 .

В конечном виде получается формула

B Z = μ o 2 R 2 ( R 2 + Z 2 ) 3 / 2

где Z - аксиальное расстояние исследуемой точки от центра кругового тока на его оси. Для случая R = z ˙ = 1 формула упрощается

B z ' = μ o 2 1 ( 1 + Z 2 ) 3 / 2 .

Для второй катушки Гельмгольца эта формула примет вид

B Z ' ' = μ o 2 1 ( 1 + ( 1 − Z ) 2 ) 3 / 2

и в целом на оси катушек Гельмгольца будет

B Z = B z ' + B Z ' ' = μ o 2 ( 1 ( 1 + z 2 ) 3 / 2 1 ( 1 + ( 1 − Z ) 2 ) 3 / 2 )

Расчеты по приведенным формулам представлены в табл.2.

Анализ табличных данных показывает, что аксиальное распределение уровня магнитной индукции представляется симметричной криволинейной зависимостью с прогрессивным спадом при удалении от центра кругового тока. Эта же зависимость для катушек Гельмгольца имеет максимум в центре системы катушек с пологим спадом при удалении от него. Поле в центре катушек превышает поля в центрах катушек на 5,3%.

Абсолютный уровень магнитного поля даже во многовитковых катушках невелик, потому что множитель, представляющий магнитную постоянную, имеет порядок 10^-7. Для полей с уровнем Iтл=10⁴ Гс требуются катушки с количеством ампервитков, измеряемых тысячами. Поэтому применение внешнего магнитопровода существенно повышает эффективность питания катушек и снижает энергозатраты на питание и охлаждение электромагнитных установок.

Радиальное распределение магнитного поля в плоскости кругового витка с током можно исследовать по схеме на фиг.5,

где а - радиальное смещение исследуемой точки по диаметру кругового тока,

r - расстояние исследуемой точки от элемента тока d ℓ → , произвольного,

R - радиус кругового тока,

φ - азимут элемента тока d ℓ → .

Для произвольной точки, лежащей на диаметре кругового витка, можно записать

{ d B → = μ o 4 π i d ℓ r 2 sin ( d ℓ →     ^ r ⇀ ) , r 2 = R 2 + а 2 − 2 R a cos φ

Действительно, h=a·sinφ, b=a·cosφ.

Следовательно, r²=h²+(R-b)²=R²+a²-2Racosφ.

Поскольку угол между элементом тока d ℓ → и вектором r → d ℓ →     ^ r ⇀ = π 2 + α , то α = arc   s i n a     s i n φ r .

В результате подстановки полученного выражения в исходную формулу закона БСЛ и последующего интегрирования получаем закон радиального распределения магнитной индукции по диаметру кругового тока

B ( a ) = μ 0 2 π i R ∫ o π 1 r 2 s i n ( π 2 + a r c s i n a s i n ϕ r ) d ϕ

Для случая R=i=1 интеграл упрощается

{ B ( a ) = μ 0 2 π ∫ o π 1 r 2 s i n ( π 2 + a r c s i n a s i n ϕ r ) d ϕ r 2 = 1 ` + a 2 − 2 a c o s ϕ

В табл. 3 представлены результаты числового интегрирования и экспериментального исследования радиального распределения магнитной индукции в плоскости кругового витка с током.

В авторском эксперименте использовался круглый виток диаметром 100 мм из медной проволоки диаметром 1 мм при токе 35 А. При токах большего значения виток нагревался докрасна. Поле измерялось измерительной катушкой диаметром 5 мм и миливольтметром. В последней графе приведены результаты исследования сверхпроводящего короткого соленоида диаметром 1,8 м, см. Хоукинс С.Р. "Сверхпроводящие соленоиды", изд Мир, 1965, с.238-258.

Анализ табличных данных показывает, что теоретический расчет автора верен и подтвержден экспериментально с достаточной точностью.

Главный вывод состоит в том, что радиальное распределение магнитной индукции в плоскости кругового витка с током неоднородно и его неоднородность растет прогрессивно по мере удаления к периферии витка, где оно возрастает многократно. Эта величина аксиально убывает, а радиально в плоскости витка растет и на центр витка приходится условный максимум типа седла.

Величину магнитной индукции вне плоскости кругового тока можно определить, если исследуемую точку поместить на плоскости, совмещенной с осью симметрии кругового тока, фиг. 6. Координаты этой точки будут: a, z, φ,

где a - расстояние исследуемой точки от оси симметрии кругового тока,

z - расстояние исследуемой точки от плоскости кругового тока,

φ - азимутальный угол.

Теперь аксиальная составляющая магнитной индукции будет определяться углом β по формуле B z ( a ,   z ) = B ( a ,   z ) s i n β = B ( a ,   z ) r ρ ,

где r²=R²+a²-2Racosφ,

ρ²=R²+a²+z²-2Racosφ.

При R= i=1 расчетная формула примет вид

{ B z ( a ,   z ) = μ 0 2 π ∫ o π r ( r 2 + z 2 ) 3 / 2 s i n ( π 2 + a r c s i n a s i n ϕ r ) d ϕ . r = 1 ` + a 2 − 2 a c o s ϕ

В табл. 4 представлены результаты расчета по этой интегральной формуле. По горизонтали представлены относительные значения величины магнитной индукции при радиальном переведении расчетной точки, а по вертикали соответственно при аксиальном ее перемещении. За 1 принято значение магнитной индукции в центре кругового тока.

Анализ содержания табл. 4 показывает, что при перемещении расчетной точки только по оси симметрии кругового тока или только по радиусу в плоскости кругового тока числовые значении магнитной индукции повторяются в соответствии с таблицами 2 и 3. Вне плоскости кругового тока радиальном перемещении расчетной точки величина магнитной индукции монотонно убывает.

В табл. 5 в относительных единицах представлено распределение магнитной индукции в диаметральной плоскости катушек Гельмгольца. Анализ содержания этой таблицы показывает, что это поле симметрично относительно плоскости z=0,5. В геометрическом центре катушек Гельмгольца поле имеет условный максимум типа седла, от которого отходят линии хребтов к центрам сечении токовозбуждающих проводников, при приближении к которым расчетная величина магнитной индукции возрастает многократно.

Неоднородность магнитного поля в центре катушек Гельмгольца зависит от размеров выбранной области. Для цилиндра высотой и диаметром 0,5 R неоднородность составляет 1,5%.

В случае катушек конечного прямоугольного сечения закон БСЛ примет вид d B = μ o 4 π j d z d r d l r 2 sin ( d ℓ →     ^ r ⇀ )

где jdzdr - элемент тока в катушке.

Величина магнитной индукции в точке, отстоящей на а от оси симметрии катушки и на z от медианной плоскости катушки, определится тройным интегралом

B ( a , z ) = μ o 2 π j ∫ R 1 R 2 ∫ − Z 1 2 Z 1 2 ∫ o π r 1 ( r 1 2 + z 2 ) 3 2 sin ( π 2 + arcsin a sin ϕ r 1 ) d ϕ d z d r

где r 1 2 = r 2 + a 2 − 2 a r cos ϕ

R₁ - внутренний радиус катушки,

R₂ - внешний радиус катушки,

Z 1 2 - половина толщины катушки.

В табл. 6 представлены результаты вычислений для R₁=1, R₂=1, 2, j=30.

Анализ содержании табл. 6 показывает, что в медианной плоскости катушки конечного сечения величина магнитной индукции тоже возрастает при удалении от центра катушки, но крутизна роста слабее, чем в тонкой одновитковой катушке. Аксиальный спад величины магнитной индукции сохраняется, но он тоже слабее.

В табл. 7 представлено диаметральное распределение величины магнитной индукции толстых катушек Гельмгольца.

В центре толстых катушек Гельмгольца магнитная индукция имеет по-прежнему максимум, но он на 15 % выше, чем в тонких при той же магнитодвижущей силе. Общий характер вариации распределения величины магнитной индукции сохраняется. Неоднородность же существенно ухудшилась и для цилиндра высотой и диаметром 0,5 R составила по высоте 3%, а по радиусу 9%.

В качестве общих выводов следует сделать следующее.

Катушки с диаметром сечения обмотки менее 0,1 диаметра катушки можно считать тонкими с достаточной инженерной точностью.

Для катушек конечного сечения обмотки получена универсальная интегральная формула для расчета величины магнитной индукции во внутреннем пространстве катушки.

При создании магнитной системы с однородным магнитным полем не следует увлекаться толстыми катушками.

У Говоркова В.А. "Электрические и магнитное поля", М., Энергия, 1968 на стр. 205-207 приведен приближенный расчет напряженности магнитного поля внутри кругового тока, на стр. 207-210 приведен расчет аксиального распределения напряженности магнитного поля тонкого соленоида.

Устройство для создания однородного магнитного поля, содержащее катушки Гельмгольца и внешний магнитопровод броневого типа, отличающееся тем, что указанный магнитопровод выполнен из верхней и нижней идентичных состыкованных торцами частей с цилиндрическими полостями для катушек Гельмгольца и исследуемых объектов, оси которых совмещены, внешние торцы магнитопровода скруглены радиусом, равным радиусу катушек Гельмгольца.