Способ определения смачиваемости мелкодисперсных порошков

Способ определения смачиваемости мелкодисперсных порошков

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования характеристик порошков, в частности их смачиваемости. Смачиваемость порошков играет важную роль в эффективности целого ряда технологических процессов - мокром пылеулавливании, пылеподавлении, флотации, фильтровании, комковании порошковых материалов, формировании керамических композиций, пропитке и т.д. [1].

Смачиваемость сажи, например, определяет процесс гранулирования и регламентирует выход сажи, используемой для резиновой промышленности, при производстве лаков и красок, а также при получении каучуков. Смачиваемость порошков угля является одним из показателей, определяющих эффективность процесса отделения минералов от пустых пород при обогащении угля [2] и технологии нейтрализации угольной пыли в шахтах [3].

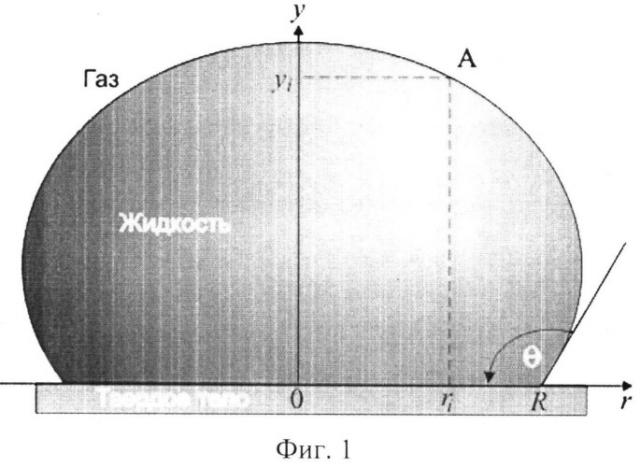
Основной характеристикой смачиваемости плоской поверхности твердого тела жидкостью является краевой угол θ [4], который отсчитывается от касательной к свободной поверхности капли жидкости, проведенной в точке раздела трех фаз (жидкой, твердой, газообразной), в сторону жидкости (Фиг.1). Известны способы определения смачиваемости твердых материалов [1, 5], основанные на измерении краевого угла по профилю капли жидкости y(r), расположенной на плоской поверхности твердого тела, путем проведения касательной в точке трехфазного контакта R (Фиг.1). Здесь y(r) - расстояние точки A профиля капли от плоской подложки для радиальной координаты r.

Для порошковых материалов такой способ определения краевого угла затруднен из-за малости размеров частиц порошка (вплоть до субмикронных) и отсутствия, как правило, плоских поверхностей у частиц. Для порошков известен ряд косвенных способов определения характеристик смачиваемости, основанных на измерении величин, связанных с явлением смачиваемости.

Известен способ определения краевого угла для порошков, заключающийся в помещении капли жидкости на пластину с нанесенным на нее тонким слоем связующего раствора и монослоем порошка [1]. При этом порошок образует слой прилипших частиц. Этот способ обладает низкой точностью, вызванной шероховатостью поверхности за счет неоднородности дисперсного состава порошка и наличием промежутков между частицами.

Известны способы определения краевого угла порошковых материалов, основанные на измерении профиля капли y(r), помещенной на брикет, полученный прессованием порошка [6, 7]. К недостаткам этих способов относятся проблема получения стационарной капли, связанная с просачиванием жидкости в поры, и деформация частиц порошка в процессе прессования брикета, в результате которой возможно нарушение идентичности частиц порошка в брикете исходным частицам.

Известен способ определения смачиваемости порошковых материалов путем измерения скорости впитывания влаги слоем порошка при контакте его с влажной поверхность [8]. При этом по результатам измерений строят кривые кинетики смачивания слоя порошка; смачиваемость тем больше, чем больше объем поглощенной влаги. Данный способ дает лишь качественную оценку смачиваемости.

Наиболее близким по технической сущности является способ определения смачиваемости порошков методом пленочной флотации [9]. Этот способ основан на определении доли массы затонувших за определенное время частиц порошка, насыпанных тонким равномерным слоем на поверхность жидкости. Массовую долю осевших частиц порошка (смоченных частиц) или параметр смачиваемости определяют по формуле

β = m c m ⋅ 100 % ,

где m_c - масса осевших частиц;

m - масса исходной навески порошка.

Данный способ также позволяет получить лишь качественную оценку смачиваемости и разделить порошки на три группы - плохо смачиваемые (β<30%), средне смачиваемые (β=30÷80%) и хорошо смачиваемые (β>80%).

Техническим результатом настоящего изобретения является разработка более точного способа определения смачиваемости порошков, обеспечивающего проведение измерений непосредственно в пылевоздушной смеси.

Технический результат изобретения достигается тем, что разработан способ определения смачиваемости мелкодисперсных порошков, основанный на расчете доли смоченных частиц порошка. В кювете с прозрачными плоско-параллельными стенками создают взвесь равномерно распределенных частиц порошка с максимальным диаметром не более 5 мкм и измеряют спектральный коэффициент пропускания зондирующего лазерного излучения взвеси, в кювету подают поток монодисперсных капель диаметром 0.8÷2.5 мм из равномерно распределенных по поперечному сечению кюветы капельниц и повторно измеряют спектральный коэффициент пропускания, причем начальную концентрацию частиц порошка выбирают из условия T₀≤0.2, промежуток времени подачи капель определяют из условия T_k>2T₀. Параметр смачиваемости β рассчитывают по формуле

β = 4 V ln [ ( ln 1 T 0 ) ( ln 1 T k ) − 1 ] η π D 2 h n f t k ,

где V - объем кюветы;

T₀, T_k - спектральный коэффициент пропускания до и после осаждения капель;

η = ( S t k S t k + 0.125 ) 2 - коэффициент захвата;

S t k = ρ p D 20 u 18 μ D - осредненное число Стокса;

ρ_p - плотность частиц порошка;

D₂₀ - среднеквадратичный диаметр частиц порошка;

u - скорость гравитационного осаждения капли;

µ - коэффициент динамической вязкости воздуха;

D - диаметр капли;

h - высота кюветы;

n - количество капельниц;

f - частота падения капель;

t_k - промежуток времени подачи капель в кювету.

Рассмотрим обоснование предлагаемого способа. В качестве характеристики смачиваемости примем массовую долю осевших на одиночной капле частиц порошка (смоченных частиц)

β = m c m ,                                                                               ( 1 )

где m_c - масса смоченных частиц порошка (осевших на каплю); m - масса частиц порошка, столкнувшихся с каплей в процессе ее гравитационного осаждения в кювете.

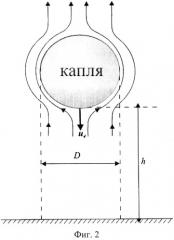
При осаждении капли жидкости диаметром D в кювете высотой h величина m рассчитывается по формуле (Фиг.2)

m = π D 2 4 h c η ,

где c - массовая концентрация частиц порошка в кювете;

η≤1 - коэффициент захвата.

Масса смоченных частиц порошка с учетом (1) равна

m c = β m = β π D 2 4 h c η .                                                        ( 2 )

При анализе осаждения частиц порошка на движущуюся каплю необходимо учитывать искривление линий тока запыленного потока пылевоздушной среды (Фиг.2). Коэффициент захвата η - это отношение числа частиц, соударяющихся с препятствием (каплей), к числу частиц, которые соударились бы, если линии тока не отклонились бы препятствием. В результате этого эффекта не все частицы, расположенные в сечении S=nD²/4 (миделевом сечении капли), столкнутся с ней. Доля столкнувшихся частиц определяется (для потенциального обтекания) формулой Лэнгмюра-Блоджетта [10]

η = ( S t k S t k + 0.125 ) 2 ,                                                            ( 3 )

где Stk - число Стокса.

Для монодисперсных частиц порошка диаметром D_p число Стокса определяется выражением

S t k = ρ p D p 2 u 18 μ D .

Поскольку взвесь порошка представляет собой совокупность полидисперсных частиц, то необходимо использовать осредненное число Стокса [10]:

S t k = ∫ 0 ∞ ρ p D p 2 ϕ ( D p ) u 18 μ D d D p = ρ p u 18 μ D ∫ 0 ∞ D p 2 ϕ ( D p ) d D p = ρ p u 18 μ D D 20 ,

где φ(D_p) - дифференциальная функция счетного распределения частиц порошка по размерам;

D 20 = ∫ 0 ∞ D p 2 ϕ ( D p ) d D p - среднеквадратичный диаметр частиц порошка.

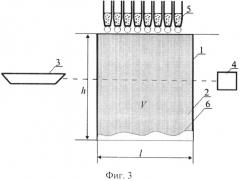
Для подачи потока монодисперсных капель в верхней части кюветы (Фиг.3) установлены n капельниц, расположенных равномерно в поперечном сечении кюветы. Все капельницы образуют капли одинакового диаметра D с частотой подачи f (количество образующихся капель в секунду). Таким образом, за промежуток времени t через кювету пройдет N капель:

N=nft.

Поскольку масса частиц порошка, осевших на одной капле, определяется формулой (2), то для N капель суммарная масса смоченных частиц равна

M c = β π D 2 4 h c N η = β π D 2 4 h c n f t η .                                                    ( 4 )

Для определения параметра смачиваемости β необходимо учесть изменение во времени массовой концентрации частиц порошка в кювете, так как некоторая доля частиц осаждается на каплях. Для этого запишем уравнение (4)в виде

d M c ( t ) = β π D 2 4 h c ( t ) n f η d t ,                                                    ( 5 )

где dM_c(t) - масса смоченных частиц за время dt.

Смоченные частицы вместе с каплями осаждаются на дно кюветы, поэтому уменьшение суммарной массы частиц M(t), взвешенных в кювете, равно

d M ( t ) = − d M c ( t ) .                                                                       ( 6 )

С учетом (6) уравнение (5) примет вид

d M ( t ) = − β π D 2 4 h c ( t ) n f η d t .

Разделив это уравнение почленно на объем кюветы V, получим:

d c ( t ) = − β B c ( t ) d t ,                                                                       ( 7 )

где

B = π D 2 4 V h n f η = c o n s t .                                                               ( 8 )

Уравнение (7) представим в виде

d c ( t ) c ( t ) = − β B d t .                                                                            ( 9 )

Интегрируя (9) в пределах от t=0 до t, получим:

ln [ c ( t ) c 0 ] = − β B t .

Отсюда следует, что

c ( t ) = c 0   exp ( − β B t ) ,                                                        ( 10 )

где c(t) - массовая концентрация частиц порошка в произвольный момент времени t>0;

c₀ - начальная массовая концентрация частиц порошка.

Из уравнения (10) можно определить параметр смачиваемости β:

β = ln [ c 0 / c ( t ) ] B t .                                                                   ( 11 )

Подставляя в (11) выражение для В из уравнения (8), получим:

β = 4 V ln [ c 0 / c k ] π D 2 h n f t k η ,                                                                    ( 12 ) ,

где c_k - концентрация в момент времени t_k, соответствующий прекращению подачи капель.

Для определения параметра смачиваемости β по формуле (12) необходимо определить массовую концентрацию частиц порошка в кювете в начальный момент времени c₀ (начало подачи капель) и после осаждения капель c_k.

Для этого равномерно распределенную в воздухе взвесь частиц порошка создают в кювете с плоско-параллельными стенками из прозрачного материала, например, оптического стекла (Фиг.3). С помощью источника зондирующего излучения (лазера) и приемника излучения измеряют спектральный коэффициент пропускания в кювете

T = I I 0 ,

где I - интенсивность прошедшего через взвесь частиц излучения;

I₀ - интенсивность излучения входящего пучка.

В соответствии с законом Бугера [11]

T=exp(-τ),

где τ=Kcl - спектральная оптическая плотность слоя частиц порошка;

K - спектральный показатель ослабления, который характеризует ослабление света единичным объемом среды, содержащим независимо рассевающие частицы;

l - ширина кюветы (толщина слоя частиц порошка).

Для слоя полидиснерсных частиц с функцией распределения φ(D_p) показатель ослабления равен [11]

K = 3 c 2 ρ p ∫ 0 ∞ Q ( α , m ¯ ) D p 2 ϕ ( D p ) d D p ∫ 0 ∞ D p 3 ϕ ( D p ) d D p ,

где

Q ( α , m ¯ ) - фактор эффективности ослабления;

α=πD_p/λ - безразмерный параметр дифракции (параметр Ми);

λ - длина волны зондирующего излучения;

m ¯ - комплексный показатель преломления материала частиц.

В предположении, что в процессе осаждения частиц порошка на каплю функция распределения φ(D_p) не изменяется, можно записать

c 0 c k = τ 0 τ k = ln ( 1 T 0 ) ln ( 1 T 0 ) ,                                                                     ( 13 )

где τ₀, τ_k - спектральная оптическая плотность слоя частиц порошка до и после осаждения капель соответственно.

Подставляя (13) в (12), получим рабочую формулу для расчета β

β = 4 V ln [ ( ln 1 T 0 ) ( ln 1 T k ) − 1 ] π D 2 h n f t k η .                                                    ( 14 )

Полученный положительный эффект изобретения связан со следующими факторами:

1. Измерение смачиваемости частиц порошка проводится непосредственно в пылевоздушной смеси. В процессе измерений порошковые материалы не подвергаются механическим воздействиям (брикетирование, полировка и т.д.).

2. Выбор диаметра капли в диапазоне 0.8÷2.5 мм связан с тем, что при осаждении в кювете капля должна сохранять сферическую форму. Согласно экспериментальным данным [12, 13] капля не деформируется и сохраняет сферическую форму при значениях числа Вебера We<0.15. В работе [13] экспериментальные данные по деформации капли аппроксимированы выражением

ψ = exp ( 0.03 W e 1.5 ) ⋅ 100 % ,                                                           ( 15 )

где ψ - мера деформации.

Скорость стационарного осаждения капель воды определялась путем решения уравнения гравитационного осаждения сферической частицы для значения коэффициента сопротивления C D = 24 / Re + 4 / Re 3 [10], где Re=ρuD/µ - число Рейнольдса; ρ - плотность воздуха; µ - коэффициент динамической вязкости воздуха.

Число Вебера рассчитывалось по формуле [10] We=ρu²D/σ, где σ - коэффициент поверхностного натяжения жидкости. Расчеты проводились для следующих значений параметров: ρ=1.205 кг/м³; ρ_l=1000 кг/м³ - плотность воды; µ=1.808·10^-5 кг/(м·с). Результаты расчетов (таблица 1) показали, что для капель воды диаметром 0.8 мм и 2.5 мм при осаждении в воздухе значение числа Вебера составляет We=0.13 и We=2.5 соответственно. Согласно (15) при данных значениях числа Вебера мера деформации формы капли не превышает ψ≈0.1÷5%. Использование капелл меньшего диаметра связано с технической проблемой получения мелкодисперсных капель. В таблице 1 приведены также экспериментально определенные значения скорости осаждения капель воды в воздухе при давлении p=100 кПа и температуре T=20°C [14], которые хорошо согласуются с расчетными данными.

Таблица 1
Параметры осаждения капли воды в воздухе
D, мм	0.1	0.5	0.8	1	1.5	2	2.5	3
u, м/с	0.25	2.01	3.15	3.9	5.5	7	7.8	8.6
uэксп, м/с	0.27	-	-	4.03	-	6.49	-	8.06
We	10-4	0.03	0.13	0.25	0.75	1.6	2.5	3.7

3. Выбор диаметра частиц порошка D_p≤5 мкм связан с тем, что при D_p>5 мкм время осаждения частиц мало и частицы быстро осаждаются на дно измерительного объема. Результаты проведенных расчетов для скорости и времени осаждения частиц угольного порошка приведены в таблице 2.

Скорость и время осаждения частиц угля рассчитывались по формулам для Стоксовского режима [10]

u p = g ρ p D p 2 18 μ , t_p=h/u_p,

где h=0.2 м - высота измерительного объема;

ρ_p=1200 кг/м³ - плотность угольных частиц.

При значении диаметра частиц D_p=5 мкм время их осаждения составляет более 2 мин. Этого времени достаточно для измерения коэффициента пропускания до и после подачи совокупности капель.

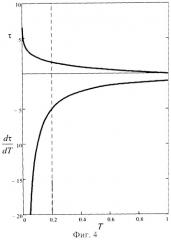
4. Выбор начального коэффициента пропускания T₀≤0.2 связан с тем, что погрешность расчета оптической плотности τ тем меньше, чем больше чувствительность τ от коэффициента пропускания. На Фиг.4 приведены зависимости τ(T) и d τ d T ( T ) , из которых видно, что при значении T₀≤0.2 наблюдается большая чувствительность оптической плотности от коэффициента пропускания.

5. Выбор T_k>2T₀ определяется из условия максимальной точности измерения коэффициента пропускания.

Таблица 2
Параметры осаждения частиц угольного порошка в воздухе
Dp=20 мкм
Stk	5.8	5.7	5.4	5.2	4.6
η	0.96	0.96	0.96	0.95	0.95
tp, с	14	14	14	14	14
Dp=10 мкм
Stk	1.5	1.4	1.4	1.3	1.2
η	0.85	0.85	0.84	0.83	0.81
tp, с	55	55	55	55	55
Dp=5 мкм
Stk	0.36	0.36	0.34	0.32	0.29
η	0.55	0.55	0.53	0.52	0.49
tp, с	221	221	221	221	221
Dp=4 мкм
Stk	0.23	0.23	0.22	0.21	0.18
η	0.42	0.42	0.40	0.39	0.35
tp, с	346	346	346	346	346
Dp=3 мкм
Stk	0.13	0.13	0.12	0.12	0.10
η	0.26	0.26	0.24	0.23	0.21
tp, с	615	615	615	615	615
Dp=2 мкм
Stk	0.06	0.06	0.05	0.05	0.05
η	0.1	0.01	0.09	0.09	0.07
tp, мин	23	L23	L23	23	23
Dp=1 мкм
Stk	CL02|	0.01	0.01	0.01	0.01
η	0.01	0.01	0.009	0.008	0.007
tp, мин	92	92	92	92	92

Сущность изобретения поясняется чертежами и графиками.

На Фиг.1 приведена равновесная форма капли, помещенной на горизонтальную твердую поверхность.

На Фиг.2 приведена схема осаждения капли.

На Фиг.3 приведена схема экспериментальной установки для определения смачиваемости порошковых материалов.

На Фиг.4 приведена зависимости оптической плотности τ и ее производной dτ/dT от коэффициента пропускания.

На Фиг.5 приведена дифференциальная функция счетного распределения частиц угольного порошка по размерам.

На Фиг.6 приведена зависимость концентрации частиц угольной пыли с распределением (16) от времени подачи капель для значения параметра смачиваемости β=0.8, рассчитанная по формуле (10).

На Фиг.7 приведена зависимость отношения оптических плотностей τ₀ и τ_k частиц с распределением (16) от времени подачи капель для значения параметра смачиваемости β=0.8, рассчитанная по формуле (13).

Пример реализации заявляемого способа (Фиг.3). В кювете 1 с прозрачными плоско-параллельными стенками создают равномерную взвесь 2 частиц порошка. С помощью лазера 3 и приемника излучения 4 измеряют спектральный коэффициент пропускания T₀ взвеси частиц. Из системы подачи капель 5 в кювету поступает поток капель в течение некоторого промежутка времени t_k. После чего повторно измеряют спектральный коэффициент пропускания T_k и определяют параметр смачиваемости частиц порошка по формуле (14).

Эффективность заявляемого способа, схема которого приведена на Фиг.2, определяли проведением прямых расчетов изменения концентрации и оптической плотности среды на примере частиц угольной пыли при их осаждении в воздухе при подаче капель воды для значений параметров, приведенных в таблице 3. Функция распределения угольных частиц, полученная с помощью установки Mastersizer 2000 (MALVERN, Великобритания), приведена на Фиг.5. Среднеквадратичный диаметр частиц равен D₂₀=1.9 мкм. Полученная функция аппроксимирована гамма-распределением

ϕ ( D p ) = 15.9 D p 5.5 exp ( − 3.6 D p ) ,                                                   ( 16 )

где [φ(D_p)]=мкм^-1; [D_p]=мкм.

Таблица 3
Значения параметров для расчета β
ρр=1200 кг/м3	µ=1.808·10-5 кг/м·с	n=50	f=2c-1
ρ=1.205 кг/м3	h=0.2 м	V=0.002 м3	η=0.53
ρl=1000 кг/м3	D=l.5 мм	c0=1000 кг/м3

Результаты расчетов представлены на Фиг.6, 7. На Фиг.6 приведена зависимость концентрации взвеси частиц угольной пыли от времени подачи капель для значения параметра смачиваемости β=0.8. На Фиг.7 приведена зависимость оптической плотности от времени подачи капель в кювету при значении β=0.8. Проверку адекватности способа можно провести, используя Фиг.6 и Фиг.7.

Выбираем промежуток времени подачи капель t_k=100 c, при котором заметно изменение начальной концентрации взвеси и выполняется условие T_k>2Т₀ для спектрального коэффициента пропускания (Фиг.6, 7). При значении времени t_k=100 c концентрация взвеси и отношение оптических плотностей равны c_k=470 кг/м³, τ₀/τ_k=2.1 соответственно.

Подставляем найденные значения в конечную формулу (14) для расчета параметра β

β = 4 ⋅ 0.002 ⋅ ln ( 2.1 ) 3.14 ⋅ ( 1.5 ⋅ 10 − 3 ) 2 ⋅ 0.2 ⋅ 50 ⋅ 2 ⋅ 100 ⋅ 0.53 = 0.8 .

Как видно из приведенного примера, заданное и рассчитанное значения параметра смачиваемости совпадают (β=0.8). Аналогичные результаты получаются и для любого значения параметра смачиваемости в диапазоне β=0÷1.0. Таким образом, предлагаемый способ позволяет повысить точность определения характеристик смачиваемости мелкодисперсных порошков и проводить измерение непосредственно в пылевоздушной смеси. Данный способ может найти применение для исследований широкого класса органических и неорганических порошковых материалов.

Литература:

1. Зимон А.Д. Адгезия жидкости и смачивание. - М.: Химия, 1974. - 416 с.

2. Годэн A.M. Основы обогащения полезных ископаемых. - М.: Государственное научно-техническое издательство литературы по черной и цветной металлургии, 1946. - 535 с.

3. Пирумов А.И. Обеспыливание воздуха. - М.: Стройиздат, 1981. - 296 с.

4. Де Жен П.Ж. Смачивание: статика и динамика // Успехи физических наук. - 1987. - Т.151. - Вып.4. - С.619-678.

5. Пат. РФ 2460987, МПК G01N 13/02. Способ определения коэффициента поверхностного натяжения и угля смачивания / М.А.Пономарева, В.А.Якутенок - №2011122481/28; заявл. 02.06.2011; опубл. 10.09.2012.

6. Kossen N.W., Heertjes P.M. The determination of the contact angle for systems with powder // Chemical Engineering Science. - 1965. - V.20. - №6. - P.593-599.

7. Пат. РФ 2457464, МПК G01N 13/00. Способ определения смачиваемости порошковых материалов / В.А. Архипов, Д.Ю. Палеев, В.Ф. Трофимов, А.С. Усанина. - №2011107818; заявл. 28.02.2011; опубл. 27.07.2012.

8. Коузов П.А., Скрябина Л.Я. Методы определения физико-химических свойств промышленных пылей. - Л.: Химия, 1983. - 143 с.

9. Биргер М.И., Вальдберг А.Ю., Мягков Б.И. Справочник по пыле- и золоулавливанию. - М.: Энергоатомиздат, 1983. - 312 с.

10. Шиляев М.И., Шиляев A.M. Аэродинамика и тепломассообмен газодисперсных потоков. - Томск.: Издательство Томского государственного архитектурно-строительного университета, 2003. - 272 с.

11. Архипов В.А., Бондарчук С.С.Оптические методы диагностики гетерогенной плазмы продуктов сгорания: учеб. пособие. - Томск: Томский государственный университет, 2010. - 265 с.

12. Гонор А.Л., Ривкинд В.Я. Динамика капли. Итоги науки и техники. Сер. Механика жидкости и газа. - М.: ВИНИТИ. 1982. Т.17. - С.86-159.

13. Раушенбах Б.В., Белый С.А., Беспалов И.В., Бородачев В.Я., Волынский М.С., Прудников А.Г. Физические основы рабочего процесса в камерах сгорания воздушно-реактивных двигателей. - М.: Машиностроение, 1964. - 525 с.

14. Матвеев Л.Т. Физика атмосферы. - СПб.: Гидрометеоиздат, 2000. - 751 с.

Способ определения смачиваемости мелкодисперсных порошков, основанный на расчете доли смоченных частиц порошка, отличающийся тем, что в кювете с прозрачными плоско-параллельными стенками создают взвесь равномерно распределенных в воздухе частиц порошка с максимальным диаметром не более 5 мкм и измеряют спектральный коэффициент пропускания зондирующего лазерного излучения взвеси, в кювету подают поток монодисперсных капель диаметром 0.8÷2.5 мм из равномерно распределенных по поперечному сечению кюветы капельниц и повторно измеряют спектральный коэффициент пропускания, причем начальную концентрацию частиц порошка выбирают из условия T₀≤0.2, промежуток времени подачи капель определяют из условия T_k>2T₀, a параметр смачиваемости рассчитывают по формуле где V - объем кюветы;T₀, T_k - спектральный коэффициент пропускания до и после осаждения капель; - коэффициент захвата; ρ_p - плотность частиц порошка;D₂₀ - среднеквадратичный диаметр частиц порошка;u - скорость гравитационного осаждения капли;µ - коэффициент динамической вязкости воздуха;D -диаметр капли;h - высота кюветы;n - количество капельниц;f - частота падения капель;t_k - промежуток времени подачи капель в кювету.