Способ персональной автономной навигации

Способ персональной автономной навигации

Иллюстрации

Показать все

Реферат

Изобретение относится к области приборостроения, в частности к способам персональной навигации (пешеходной, автомобильной и пр.), и может быть использовано при решении задач локальной навигации (мининавигации): для задач автономной навигации при проведении геологической, геофизической и военной разведки; навигации наземных транспортных средств при изыскании, строительстве и мониторинге дорог, трасс, трубопроводов; пешеходной или автомобильной навигации в неизвестной малоизученной местности или в пределах незнакомого города; технологической навигации мобильных роботов в закрытых пространствах при выполнении аварийно-спасательных работ в чрезвычайных ситуациях; групповой (корпоративной) навигации для осуществления походов и путешествий (в области альпинизма, спорта, охоты, рыболовства, активного отдыха на природе и пр.).

Известен угломерно-дальномерный способ персональной автономной навигации (журнал «Гироскопия и навигация», №4,2004, с.50-75), в котором направление движения объекта (пешехода или его индивидуального транспортного средства) определяется по показаниям цифрового магнитного компаса (ЦМК) и гироскопа (взаимно корректирующих друг друга), а величина пройденного пути определяется с помощью хорошо откалиброванного инерциального измерительного модуля на основе реализации интегрального алгоритма инерциального счисления пройденного пути и использования шагомера.

В данном способе геомагнитная информация используется только для определения направления движения пешехода или его транспортного средства. Информация о магнитном поле Земли (МПЗ) непосредственно для целей навигации (т.е. для определения координат местоположения объекта) в этом способе не используется. Однако ошибки интегрального инерциального способа счисления пути и ошибки шагомера в этом способе остаются.

Недостаток угломерно-дальномерного способа персональной автономной навигации на основе использования информации от ЦМК, гироскопа инерциального модуля и шагомера заключается в недостаточно высокой точности навигации, обусловленной накоплением погрешности во времени и в зависимости от пройденного пути.

Также известен способ персональной навигации, основанный на использовании сигналов глобальных спутниковых навигационных систем (GPS, ГЛОНАСС, Бэйдоу, Galileo). Использование способа спутниковой навигации для целей персональной навигации отражено в ряде заявок и патентов (US 20050033515 А1, опубл. 10.02.2005 г.; US 20070282565 А1, опубл. 06.12.2007 г.) и реализовано в многочисленных производственных образцах фирм Garmin, GlobalSat, Magellan и др., широко применяемых на практике.

Персональные спутниковые навигаторы обеспечивают высокоточное определение всех координат (φ, λ, r) точек текущего местоположения подвижного объекта (ПО), на котором находится навигатор. Однако этот способ не является автономным. Кроме того, реализация этого способа на практике характеризуется значительной сложностью: большими материальными, техническими, технологическими и финансовыми затратами, высокой себестоимостью, невысоким показателем помехоустойчивости, отказоустойчивости и доступности в любой точке околоземного пространства. Недостатками данного способа навигации являются такие реальные факторы, как многолучевость антенн спутников и навигатора; вредное влияние ионосферы Земли на радиосигналы навигационных спутников; влияние неполной и нерациональной геометрической конфигурации навигационных спутников (альманаха навигационных спутников); вредное влияние фактора «затенения» радиосигналов навигационных спутников наземными объектами.

В этих условиях приходится искать альтернативное решение, способное обеспечить достойную конкуренцию способу спутниковой навигации. В качестве такого альтернативного конкурентоспособного решения в настоящее время считается интегрированный способ инерциально-спутниковой навигации, в котором объединены два способа: способ спутниковой навигации и способ инерциальной навигации. При этом за счет интеграции двух способов навигации в одном способе обеспечивается взаимное подавление недостатков каждого отдельного способа и усиление их достоинств.

Известен способ определения параметров навигации (патент RU №2338160 от 10.11.2008 г.), в котором для достижения высоких показателей точностей навигации осуществляют комплексирование сигналов спутниковой и инерциальной навигационных систем. Путем сравнения показаний этих систем определяют скорректированные параметры навигации и величины ошибок значений параметров, вырабатываемых инерциальной навигационной системой. Затем осуществляют передачу вычисленных по эти ошибкам величин поправок в инерциальную навигационную систему для коррекции вырабатываемых ею в последующие моменты времени параметров навигации.

Недостатки интегрированного способа инерциально-спутниковой навигации заключаются в том, что этим способом не обеспечивается полная автономность решения задачи персональной навигации. Кроме того, интегрированные персональные навигаторы, работающие по способу комплексной обработки информации, отличаются относительной сложностью, ненадежностью, дороговизной и необходимостью реализации алгоритмов вычисления навигационных невязок (алгоритмов RAJM - технологий).

Известны также способы навигации по аномальным геофизическим полям, основанные на обзоре этих полей и последующей обработке полученной при обзоре многомерной информации с использованием алгоритмов поиска экстремумов, базирующихся на корреляционно-экстремальных принципах вычисления корреляционных функций и определения их экстремумов (И.Н.Белоглазов, Г.И.Джанжгава, Г.П.Чигин. Основы навигации по геофизическим полям. - М.: Наука, 1985. - с.5-19). Эти способы относятся к типу обзорно-сравнительных способов (сравнение реализации наблюдения с эталоном-шаблоном), они удовлетворяют условиям автономности, высокой информативности и точности. Однако они сравнительно ненадежны и сложны, требуют реализации достаточно сложных алгоритмов хранения первичной информации (в виде шаблонов - цифровых карт аномальных геофизических полей) и обработки текущей информации (алгоритмов поиска экстремумов, сравнения, рекурсии). Кроме того, эти способы практически непригодны для целей персональной навигации из-за невозможности реализации обзора аномальных геофизических полей, формирования текущей информации и построения соответствующих коореляционных функций при наблюдении за этими полями в одной точке (точке нахождения наблюдателя с навигатором на поверхности Земли).

Наиболее близким к предлагаемому изобретению является способ автономной инерциальной безынтегральной начальной выставки навигационных систем («Гироскопия и навигация», №2, 2003, с.65-78), принятый за прототип, заключающийся в том, что на основе инерциальной информации о векторе напряженности поля тяжести g ¯ Земли и векторе угловой скорости суточного вращения Ω ¯ планеты, получаемой в режиме остановки основания (в режиме ZUPT) в проекциях на оси связанной (приборной) системы координат XYZ, с использованием алгоритмов инерциальной безынтегральной выставки (алгоритмов гиро-горизонт-широт-компасирования) определяются в любой произвольной точке на поверхности Земли А (φ, λ, r) географическая широта (φ) и углы ориентации основания (ψ; ϑ; γ).

В настоящее время алгоритм гиро-горизонт-широт-компасирования используется на практике только для решения задачи начальной выставки инерциальных навигационных систем и не используется для решения автономной навигации.

Недостаток этого способа (прототипа) заключается в том, что он не дает возможности решать задачу автономной навигации в полном объеме (не позволяет определять две другие географические координаты: долготу (λ) и радиус-вектор (r), что сужает область применения этого способа для определения географических координат объекта.

Задача настоящего изобретения заключается в разработке комплексного инерциально-магнитометрического способа персональной автономной навигации, обеспечивающего полное определение географических координат местоположения наблюдателя (φ, λ, r) в реальном масштабе времени на основе расширения информации о параметрах геофизических полей (поля тяжести Земли - g ¯ ; поля векторов угловых скоростей вращения Земли - Ω ¯ ; нормального геомагнитного поля - T ¯ ) коррекции и обработки полученной многомерной информации по комплексным безынтегральным алгоритмам персональной автономной геофизической навигации, что обеспечивает автономность определения географических координат объекта, достоверность и полноту получения параметров навигации для объекта и отсутствие накапливающихся погрешностей измерений и вычислений навигационных параметров объекта при пройденном пути в реальном масштабе времени.

Поставленная задача достигается путем получения в режиме остановки основания объекта по двум каналам инерциальных измерений комплексной информации о параметрах геофизических полей - напряженности g ¯ поля тяжести Земли и угловой скорости Ω ¯ суточного вращения планеты и вычисления на основании полученной инерциальной информации по алгоритмам аналитического гиро-горизонт-широт-компасирования географической широты φ и параметров ориентации основания объекта: курса ψ, тангажа ϑ, крена γ; новым является то, что в дополнение к двум каналам инерциальных измерений организуют третий канал путем проведения операции идентификации магнитных свойств основания объекта, измерения вектора напряженности T ¯ магнитного поля Земли, его коррекции и сравнения оценок векторов напряженностей МПЗ T ¯ ∧ g и T ¯ ∧ g H , вычисленных для контрольной А и базовой A₀ точек маршрута, и определение по алгоритмам дифференциальной геомагнитной навигации оценок вариаций ( Δ r ¯ ∧ ) и координат ( r ¯ ∧ ) текущих контрольных точек маршрута и дополнительных навигационных параметров - географической долготы λ и радиуса - вектора r.

Согласно предлагаемому решению на основе расширения, коррекции и использования комплексной (инерциальной ( g ¯ ; Ω ¯ ) и магнитометрической ( T ¯ )) информации применительно к области персональной автономной геофизической навигации обеспечивается возможность не только вычисления географической широты (φ) гравиметрическим и тахометрическим методами, но и определения географической долготы (λ) и географического радиуса - вектора (r) (магнитометрическим методом) в реальном масштабе времени.

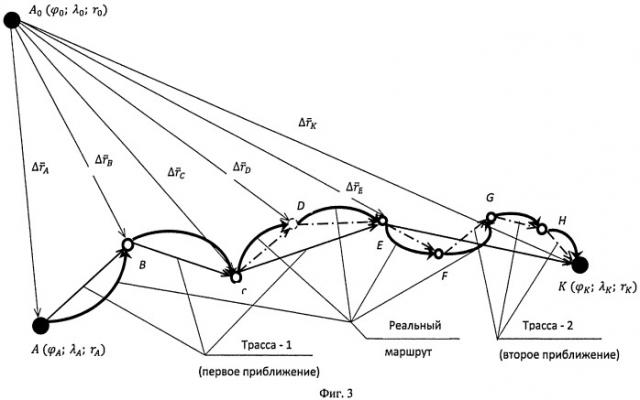
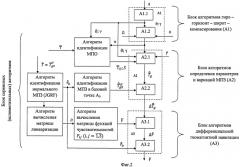
Предлагаемое изобретение поясняется чертежами. На Фиг.1 представлена схема способа персональной автономной геофизической навигации. На Фиг.2 представлена схема, иллюстрирующая последовательность реализации алгоритмов персональной автономной геофизической навигации при прохождении пешеходом маршрута. На Фиг.3 представлена схема формирования маршрута пешехода (или транспортного средства) с использованием персонального геофизического навигатора, работающего по алгоритмам персональной автономной геофизической навигации.

Способ автономной персональной геофизической навигации заключается в следующем.

1. В режиме остановки основания объекта в контрольных точках маршрута определяют комплексную информацию о параметрах геофизических полей - напряженности g ¯ поля тяжести Земли и угловой скорости Ω ¯ суточного вращения Земли:

1) гравиметрическую информацию (ГМ - информацию, получаемую с использованием трехкомпонентного блока гравиметров-акселерометров ( α ¯ = [ a x a y a z ] T ) ;

2) тахометрическую информацию (ТМ-информацию), получаемую с помощью трехкомпонентного блока гиротахометров (например, прецизионных волоконно-оптических гироскопов - ВОГ)

( Ω ¯ = [ Ω x Ω y Ω z ] T ) .

1. По алгоритмам гиро-горизонт-широт-компасирования вычисляют географическую широту φ и параметры ориентации основания объекта - курс ψ, тангаж ϑ, крен γ.

3. Выполняют операцию идентификации магнитных свойств основания объекта.

4. Далее получают и используют расширенную геофизическую информацию - магнитометрическую информацию (ММ-информацию), получаемую с помощью трехкомпонентного блока навигационных магнитометров (например, прецизионных магнитометров - феррозондов) ( T ¯ = [ T x T y T z ] T ) .

5. Осуществляют коррекцию полученного вектора напряженности T ¯ и сравнение оценок векторов напряженностей МПЗ T ¯ ∧ g и T ¯ ∧ g H , вычисленных для контрольной А и базовой A₀ точек маршрута.

6. Вычисляют по алгоритмам дифференциальной геомагнитной навигации оценки вариаций ( Δ r ¯ ∧ ) и координат ( r ¯ ∧ ) текущих контрольных точек маршрута и дополнительные параметры навигации - географическую долготу λ и радиус - вектор r.

Данную комплексную геофизическую информацию получают, накапливают и обрабатывают (Фиг.1, 2) дискретно в режиме остановок в контрольных точках маршрута (Фиг.3). Полученную комплексную геофизическую информацию обрабатывают по трем каналам измерений: гравиметрическому ( g ¯ ), тахометрическому ( Ω ¯ ) и магнитометрическому ( T ¯ ). В канале гравиметрических измерений реализуют алгоритм аналитического горизонтирования основания навигатора, тахометрический канал работает по алгоритму аналитического гиро-горизонт-широт-компасирования, а в магнитометрическом канале реализуют алгоритм дифференциальной геомагнитной навигации. В результате такой комплексной обработки информации по алгоритмам персональной автономной геофизической навигации в совокупности по всем трем каналам измерений вычисляют координаты текущего местоположения объекта r ¯ (φ; λ; r).

С помощью алгоритма работы канала гравиметрических измерений ( g ¯ ) обеспечивают определение углов крена γ_i и тангажа ϑ_i корпуса навигатора в каждом i-м сеансе измерений в режиме остановки основания объекта:

sin ϑ i = − a x i g ; cos ϑ i = a y i 2 + a z i 2 g sin γ i = a z i a y i 2 + a z i 2 ; cos γ i = − a y i a y i 2 + a z i 2 } ( i = 1, n ¯ )   ( 1 )

где α_xi; α_yi; α_zi - показания соответствующих акселерометров в i-м сеансе измерений

( i = 1, n ¯ ) ;

g - напряженность поля тяжести Земли в точке местоположения наблюдателя.

Причем

g = α x i 2 + α y i 2 + α z i 2   ( i = 1, n ¯ )   ( 2 )

Для упрощения решения задачи измерений по гравиметрическому каналу измерений горизонтирование корпуса объекта может быть выполнено не алгоритмически с использованием формул (1)-(2), а физически (с обеспечением условия механического горизонтирования ϑ=γ=0) с использованием пузырьковых микроуровней, встроенных в корпус навигатора.

На основе алгоритма работы канала тахометрических измерений ( Ω ¯ ) обеспечивают определение углов курса ψ_i корпуса объекта и географической широты φ месторасположения объекта в каждом i-м сеансе измерений в режиме остановки основания объекта:

sin ϕ = Ω x sin ϑ + ( Ω y cos γ − Ω z sin γ ) cos ϑ Ω cos ψ = Ω ⋅ sin ϕ cos ϑ − Ω y cos γ + Ω z sin γ Ω cos ϕ sin ϑ cos ψ = Ω x − Ω sin ϕ sin ϑ Ω cos ϕ cos ϑ   ( 3 )

При этом принимают Ω=2π/Т_з (Т_з - звездные сутки, T_з=23 ч 56 мин 4,091 с=86164,091 с).

Ω = 2 π T з = 7,2921158 ⋅ 10 − 5 с − 1 = 15,041 г р а д ч = 15,041069   у г л .   с е к / с   ( 4 )

Из анализа выражений (1)-(4) видно, что блок гравиметров (акселерометров) с вычислителем выполняет функцию аналитического горизонта, а блок гироскопов (тахометров) с вычислителем выполняет функции аналитического гиро-широт-компаса. Роль долготно-высотного измерителя (измерителя долготы λ и радиуса-вектора r) выполняет в предлагаемом способе магнитометрический канал измерений, который организуют путем определения вектора напряженности T ¯ и его коррекции при предварительном определении (идентификации) магнитных свойств основания объекта.

В отличие от каналов гравиметрических и тахометрических измерений канал магнитометрических измерений является более информативным, но вместе с тем и менее помехозащищенным.

Показания блока магнитометров с учетом параметров нормального МПЗ и магнитных свойств основания объекта описываются уравнением Пуассона в векторно-матричной форме:

T ¯ = ( S + E ) ⋅ A y ⋅ A ϑ ⋅ A ψ ⋅ T ¯ g + T ¯ п ,   ( 5 )

где T ¯ - вектор показаний блока магнитометров в приборной (связанной) системе координат XYZ,

T ¯ g - вектор напряженности геомагнитного поля в осях нормальной земной системы координат X_gY_gZ_g (ГОСТ 20058-80),

T ¯ п - вектор постоянной составляющей магнитного поля объекта (МПО) и навигатора в приборной системе координат XYZ,

S - матрица коэффициентов индуктивной составляющей МПО,

Е - единичная матрица (3×3).

Решение векторно-матричного уравнения (5) модно представить в следующем виде:

T ¯ ∧ g = A ψ T ⋅ A ϑ T ⋅ A γ T ⋅ ( S + E ) − 1 ⋅ ( T ¯ − T ¯ п ) .   ( 6 )

Или в развернутой форме:

[ T ^ x g T ^ y g T ^ z g ] = A ψ T A ϑ T A γ T ⋅ [ a + 1 b c d e + 1 f g h k + 1 ] − 1 ⋅ [ T x − P T y − Q T z − R ] .   ( 7 )

где T ^ x g ; T ^ y g ; T ^ z g - оценки параметров нормального МПЗ в проекциях на оси системы координат X_gY_gZ_g;

Т_х; T_y; T_z - показания соответствующих магнитометров в проекциях на оси XYZ;

A ψ T ; A ϑ T ; A γ T - транспонированные матрицы ориентации корпуса навигатора (по курсу ψ, тангажу ϑ и крену γ).

Выражения (6) или (7) представляют собой алгоритм определения вектора напряженности нормального МПЗ T ¯ g , вычисленного по показаниям блока магнитометров T ¯ = [ T x T y T z ] T . При этом информацию об углах ориентации корпуса объекта (ϑ, γ, ψ) получают в режиме остановки основания объекта по каналам гравиметрических и тахометрических измерений в соответствии с алгоритмами гиро-горизонт-широт-компасирования (1)-(4).

Информацию о магнитных свойствах основания объекта (информацию о матрице S и векторе T ¯ П ) получают, воспользовавшись методикой, технологией и алгоритмами идентификации МПО (изложенными в патенте РФ №1633930, опубл. 20.01.1996 г.). Если же объект или навигатор не обладают собственным магнитным полем (МПО), то P=Q=R=S=0.

С другой стороны, в соответствии с теорией геомагнитного потенциала выражения для компонент вектора T ¯ g представляют в виде разложения его в сферический ряд Гаусса:

T ^ x g H = ∑ n = 1 ∞ ( R r ) n + 2 ∑ m = 0 n ( g n m cos m λ + h n m sin m λ ) ⋅ ∇ P n m

T ^ y g H = ∑ n = 1 ∞ ( n + 1 ) ⋅ ( R r ) n + 2 ∑ m = 0 n ( g n m cos m λ + h n m sin m λ ) ⋅ P n m ( sin ϕ )   ( 8 )

T ^ z g H = ∑ n = 1 ∞ ( R r ) n + 2 ∑ m = 0 n m ⋅ ( g n m sin m λ − h n m cos m λ ) ⋅ P n m ( sin ϕ ) cos ϕ

где T ^ x g H ; T ^ y g H ; T ^ z g H - оценки проекций вектора напряженности нормального МПЗ на оси X_gY_gZ_g;

R - средний радиус Земли (R=6371110 м),

r - модуль радиуса вектора r ¯ (φ, λ, r),

P n m ( sin ϕ ) - присоединенные функции Лежандра n-й степени порядка m (зависят от географической широты φ),

∇ P n m - широтный градиент первого порядка n-й степени m-го порядка присоединенной функции Лежандра P n m ( sin ϕ ) (m≥0, n = 1, m ¯ ),

g n m ; h n m - коэффициенты гармонического ряда разложения (коэффициенты Гаусса-Шмидта).

Оценки T ^ x g H , T ^ y g H , T ^ z g H вычисленные по формулам (8), отличаются от оценок T ^ x g ; T ^ y g ; T ^ z g , вычисленных по показаниям блока магнитометров по формулам (6) или (7), на величины разностей, не превышающих погрешностей измерений и вычислений. Практически эти оценки совпадают. Численные значения коэффициентов Гаусса-Шмидта представляются геофизической службой глобальных наблюдений за МПЗ на каждый пятилетний период (эпоху) в соответствии с принятой моделью JGRF Международного геомагнитного поля World Magnetic Model for 2010-2015-WMM-2010 (сайт сети Internet http://www.ngdc.noaa.gov. режим доступа свободный), широко используемый в геофизике. Размерность модели WMM-2010 (n-й степени порядка m, m = 1, n ¯ , n = 0, ∞ ¯ ) выбирают в зависимости от требований к точности воспроизведения геомагнитного поля в навигаторе.

Уравнения (8) задают в общем и в явном виде зависимости параметров МПЗ ( T x g H ; T y g H ; T z g H ) от навигационных параметров - координат местоположения объекта (φ, λ, r). Однако эти уравнения не приспособлены для целей навигации в связи с тем, что эти зависимости существенно нелинейные, не позволяющие выразить в общем и явном виде обратные зависимости навигационных координат (φ, λ, r) от параметров наблюдения за геомагнитным полем. Для преодоления указанного недостатка используют дифференциальный подход, основанный на методе линеаризации (методе Ньютона). Тогда вместо выражений (8) можно написать линеаризованные функции:

T ^ g = [ T ^ x g H T ^ y g H T ^