2525262 - Способ анализа кроны и места произрастания березы на склоне оврага

Способ анализа кроны и места произрастания березы на склоне оврага

Иллюстрации

Показать все

Изобретение относится к дендрометрии и может быть использовано для разработки экологических и климатических технологий, а также при дендроэкологическом мониторинге за развитием овражной сети и рационализации землепользования. Способ анализа включает выбор поперек склона пробной полосы леса с расположенными вдоль нее деревьями. У каждой березы на пробной полосе вдоль склона измеряют высоту кроны и угол местного склона поперек общего склона у комля дерева. Для анализа роста и развития высоты кроны березы, произрастающей на склоне, по множеству измеренных параметров высоты кроны берез и угла местного склона места их произрастания статистическим моделированием выявляют взаимосвязь между высотой кроны березы и углом местного склона места ее произрастания. Такая технология позволит обеспечить защиту земельных участков около оврагов и холмов от водной эрозии. 1 з.п. ф-лы, 6 ил.

Реферат

Изобретение относится к дендрометрии при изучении влияния склона оврагов и холмов на рост и развитие кроны березовых деревьев с учетом места произрастания каждой березы на этом склоне, разработке мероприятий по защите земельных участков около оврагов и холмов от водной эрозии и может быть использовано для разработки экологических и климатических технологий, а также при дендроэкологическом мониторинге за развитием овражной сети и рационализации землепользования с учетом изменений высоты кроны растущих на склоне оврага или холма березовых деревьев.

Известен способ анализа древесного ствола по патенту №2254707, включающий разметку ствола на секции кратной или некратной длины в зависимости от расположения неровностей ствола с измерением соответствующих расстояний от корневой шейки, секции некратной длины размечают на неровностях комлевой части ствола, по крайней мере, дважды в трех точках неровности, а измерения вдоль и поперек ствола по секциям выполняют гибкой мерной лентой, причем поперек ствола измеряют гибкой мерной лентой периметр сечения ствола.

Недостатком является то, что измерения выполняют у деревьев, растущих на ровной местности. При этом известный способ не позволяет учитывать влияние комля ниже корневой шейки деревьев. Кроме того, в анализе ствола не учитывается крона деревьев. Причем березы могут произрастать на склоне оврага, сильно изменяя угол местного склона и пытаясь поднять крону выше за счет формирования небольшого холмика на общем склоне оврага или холма, а также общего склона берега малой реки или озера.

Известен также способ анализа комля растущего дерева для определения поперечного профиля оврага по патенту №2416193 РФ, характеризующийся тем, что поперек оврага выбирают пробную полосу леса с расположенными вдоль нее деревьями, измеряют расстояния и общий угол склона в поперечном сечении оврага между серединами диаметров корневой шейки смежных вдоль пробной полосы деревьев.

Недостатком является отсутствие измерений высоты кроны растущего дерева, что не позволяет изучать влияние размера кроны на место произрастания в виде угла местного склона каждого дерева на общем склоне оврага или холма. Кроме того, в дендрометрии до сих пор не выделены те лимитирующие факторы дерева, которые влияют на параметры места произрастания отдельного дерева или популяции деревьев на пробной площади.

Технический результат - расширение функциональных возможностей анализа параметров деревьев березы, произрастающих на склоне оврага или холма, в частности при сопоставлении высоты кроны с углом местного склона на общем склоне оврага, холма или иного ландшафтного объекта. По другим породам деревьев нужны другие научные исследования.

Этот технический результат достигается тем, что способ анализа кроны и места произрастания березы на склоне оврага, характеризующийся тем, что поперек оврага выбирают пробную полосу леса с расположенными вдоль нее деревьями, измеряют расстояния и общий угол склона в поперечном сечении оврага между серединами диаметров корневой шейки смежных вдоль пробной полосы деревьев, отличающийся тем, что у каждой березы на пробной полосе вдоль оврага дополнительно измеряют высоту кроны и угол местного склона поперек общего склона у комля, а по множеству измеренных берез выполняют статистическое моделирование идентификацией многочленной однофакторной математической модели.

По множеству измеренных высот кроны берез и угла склона мест их произрастания выполняют статистическое моделирование идентификацией многочленной однофакторной математической модели вида:

ϕ 1 = a 1 exp ( a 2 H к р а 3 ) ,

ϕ 2 = a 4 H к р а 5 exp ( − a 6 H к р а 7 ) ,

y i = b 1 i H к р b 2 i exp ( − b 3 i H к р b 4 i ) cos ( π Н к р / ( b 5 i + b 6 i H к р b 7 i ) − b 8 i ) ,

где φ - угол местного склона для места произрастания, град;

φ₁ - первая детерминированная составляющая модели в виде устойчивого закона экспоненциального роста угла местного склона в зависимости от высоты кроны у множества измеренных берез, град;

φ₂ - вторая детерминированная составляющая модели в виде устойчивого биотехнического закона, показывающего стрессовое возбуждение мест произрастания популяции берез (по-видимому, при адаптации этого места произрастания к водной эрозии почвы на склоне оврага или холма) по ускоренному увеличению угла местного склона на каком-то интервале изменения высоты кроны деревьев в популяции берез, град;

y_i - волновые составляющие модели, показывающие колебательное возмущение места произрастания по углу местного склона в зависимости от изменения высоты кроны деревьев в популяции берез, град;

i - номер волновой составляющей в виде асимметричного вейвлет-сигнала о колебательном взаимодействии кроны у популяции берез с местами их произрастания, шт.;

m - общее количество волновых функций, зависящее от вычислительной возможности программной среды (CyrveExpert дает только две дополнительные составляющие, то есть только до 19 параметров модели) и погрешности измерений (измерение угла в один градус и высоты в один метр дали возможность получить четырехчленную модель с коэффициентом корреляции более 0,9;

Н_кр - высота кроны дерева, м;

а₁…а₇, 6₁…6₈ - параметры статистической модели, численные значения которых выявляются в программной среде при обработке конкретных массивов данных измерений (высота кроны и угол местного склона места произрастания) по всем березам из каждой популяции.

Сущность технического решения заключается в том, что наиболее часто на склонах оврагов в лесостепной зоне России произрастают березы естественного происхождения. Они закрепляют овраги от водной эрозии, и происходит симбиоз между березняком и почвой на склоне оврага: березы своими корнями защищают почву от смыва, а почва наращивает свое плодородие, позволяя расти березам продуктивно без потери питательных веществ.

Сущность технического решения заключается также в том, что именно береза обладает замечательным свойством стать древесным растением для климатических и экологических технологий по изменению местного климата лесостепной зоны (стабилизируя температуру и водный баланс в почве в течение года) на земельных участках, подверженных водной эрозии, и предотвращает дальнейшее развитие овражной сети.

Сущность технического решения заключается также и в том, что в некоторых природно-антропогенных условиях частично восстанавливается полноводность и регулярность водотока в течение года на дне оврага.

Сущность технического решения заключается также и в том, что факторный анализ множества измеренных параметров берез и места каждой березы по углу местного склона на общем склоне оврага показал наибольшую тесноту факторной связи между углом местного склона места произрастания каждой из 30 измеренных берез и высотой кроны этих же берез.

Положительный эффект достигается тем, что выявление среднестатистической закономерности изменения угла местного склона места произрастания берез на пробной площади, заложенной на склоне оврага или холма, в зависимости от высоты кроны, позволяет проводить экологический мониторинг за состоянием и развитием самого оврага на участке с изучаемым березняком. Это позволит даже дистанционно следить за укреплением склонов оврагов и холмов от водной эрозии в ходе роста и развития посаженных берез.

Такой мониторинг, по мере накопления опыта и данных измерений, даст возможность рекомендовать экологические и климатические технологии вначале на территориях лесостепной зоны России, а затем и в степной зоне. Это, по опыту США (с 1960 года) и Китая (с 1970 года), значительно повысит урожайность зерновых культур на полях около оврагов и холмов, а также повысит продуктивность травяного покрова пойменных лугов на склонах оврагов со ставшими полноводными от влияния водных потоков ручейками, а также на склонах холмов и берегов малых рек и их притоков.

Новизна технического решения заключается в том, что впервые измерения проводят ниже корневой шейки ствола растущего дерева по углу местного склона места произрастания дерева, что позволит в будущем подойти к поиску научно-технических решений и по изучению изменений формы кроны дерева и ее влияния на параметры места произрастания. Кроме того, научная новизна заключается в том, что впервые получена математическая закономерность влияния высоты кроны у берез на изменение угла местного склона на месте произрастания каждой березы.

Предлагаемое техническое решение обладает существенными признаками, новизной и значительным положительным эффектом. Материалов, порочащих новизну технического решения, нами не обнаружено. Поэтому предлагаемое изобретение становится обоснованным научно-техническим решением, полученным на основе выявления фундаментальной закономерности влияния параметра кроны березы на параметр места ее произрастания.

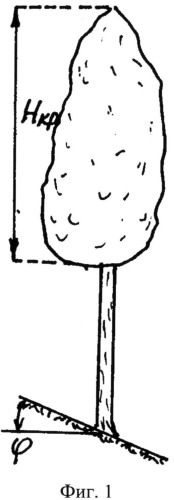
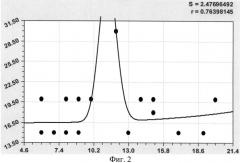
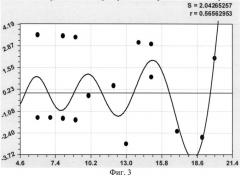
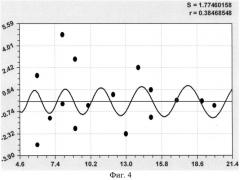
На фиг.1 приведена схема измерения высоты кроны и места произрастания березы: φ - угол местного склона для места произрастания; Н - высота кроны, измеряемая крономером, эклиметром или другими известными дендрометрическими приборами; на фиг.2 показан график детерминированной модели φ=f(Н_кр) с двумя устойчивыми законами; на фиг.3 показан график третьей составляющей математической модели в виде волновой функции; на фиг.4 - то же на фиг.3 четвертой составляющей; на фиг.5 дан график общей математической (статистической) модели φ=f(Н_кр) с четырьмя составляющими; на фиг.6 показан график остатков, то есть абсолютных погрешностей, после модели φ=f(Н_кр) с четырьмя составляющими.

Способ анализа кроны и места произрастания березы на склоне оврага выполняется следующими действиями.

Вначале выбирают по прототипу пробную площадь с березами, в виде полосы на склоне вдоль оврага, а также холма, малой реки, озера или другого элемента рельефа или ландшафта. На этой полосе выбирают учетные деревья для измерений. Для измерений высоты кроны и угла местного склона в простейшем случае применяют крономер (или эклиметр) и транспортир с отвесом на гибкой нитке.

ϕ 1 = a 1 exp ( a 2 H к р а 3 ) ,

ϕ 2 = a 4 H к р а 5 exp ( − a 6 H к р а 7 ) ,

y i = b 1 i H к р b 2 i exp ( − b 3 i H к р b 4 i ) cos ( π Н к р / ( b 5 i + b 6 i H к р b 7 i ) − b 8 i ) ,

где φ - угол местного склона для места произрастания, град;

φ₁ - вторая детерминированная составляющая модели в виде устойчивого биотехнического закона, показывающего стрессовое возбуждение мест произрастания популяции берез (по-видимому, при адаптации этого места произрастания к водной эрозии почвы на склоне оврага или холма) по ускоренному увеличению угла местного склона на каком-то интервале изменения высоты кроны деревьев в популяции берез, град;

Н - высота кроны дерева, м;

a₁…a₇, b₁…b₈ - параметры статистической модели, численные значения которых выявляются в программной среде при обработке конкретных массивов данных измерений (высота кроны и угол местного склона места произрастания) по всем березам из каждой популяции.

Способ анализа кроны и места произрастания березы на склоне оврага, например, с ручейком на дне оврага, имеющего на склоне березняк естественного происхождения, реализуется следующим образом.

У каждой березы на пробной полосе вдоль оврага дополнительно измеряют высоту кроны и угол местного склона, а по множеству измеренных берез выполняют статистическое моделирование идентификацией многочленной однофакторной математической модели.

По множеству крон измеренных берез и мест их произрастания по углу местного склона выполняют статистическое моделирование по формуле:

ϕ 1 = a 1 exp ( a 2 H к р а 3 ) ,

ϕ 2 = a 4 H к р а 5 exp ( − a 6 H к р а 7 ) ,

y i = b 1 i H к р b 2 i exp ( − b 3 i H к р b 4 i ) cos ( π Н к р / ( b 5 i + b 6 i H к р b 7 i ) − b 8 i ) ,

где φ - угол местного склона для места произрастания, град;

Н - высота кроны дерева, м;

Пример. Для снижения линейной эрозии почвы оврагами применяют растения. Цель исследования - изучение формы комля деревьев, растущих в овраге, для выявления закономерностей взаимодействия между древесными растениями и склоном. Объектом исследования был лесной овраг около деревни Ямолино Горномарийского района Республики Марий Эл. Эксперименты были проведены летом 2011 года.

Методика измерения дерева выполняется следующим образом (фиг.1).

Сначала определяли участок оврага по методике, изложенной в патенте №2416193 РФ по прототипу, на склоне которого растут деревья. Выбрали учетные деревья для измерений в количестве 30 штук. Для измерений применяли гибкую мерную ленту и транспортир с отвесом.

После факторного анализа 14 измеренных параметров комля и места произрастания берез оказалось, что имеются сильная факторная связь влияния высоты кроны на угол местного склона места произрастания деревьев. При этом обратное влияние угла местного склона на высоту кроны березы по коэффициенту корреляции составляет менее 0,3. Поэтому прямое влияние φ=f(Н_кр) является высокоадекватным.

По принципу «от простого к сложному» можно предложить (табл.1) «кирпичики» для построения, по ходу структурно-параметрической идентификации биотехнического закона, любой статистической модели.

Таблица 1
Математические конструкты для построения статистической модели
Фрагменты без предыстории изучаемого явления или процесса	Фрагменты с предысторией изучаемого явления или процесса
у=ax - закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы)	у=а - закон не влияния принятой переменной на показатель, который имеет предысторию значений
у=ax^b - закон показательного роста (закон показательной гибели y=ax^-b не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной	у=аехр(±cx) - закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создан метод операторных исчислений
y=ax^bexp(-cx) - биотехнический закон в упрощенной форме	у=aexp(±cx^d) - закон экспоненциального роста или гибели, - по автору статьи
у=ax^bexp(-cx^d) - биотехнический закон, предложенный проф. П.М.Мазуркиным

В таблице 1 показаны все «нормальные» фрагменты, у которых впереди могут быть расположены оперативные константы, в виде знаков «+» или «-». Все шесть устойчивых законов распределения являются частными случаями биотехнического закона, показанного внизу таблицы 1.

Как известно из классической математической статистики, грубая классификация уровней коэффициента корреляции следующая:

а) до 0,3 - нет связи между факторами (то есть можно не учитывать эти связи, хотя они в других условиях проявления могут оказаться даже сильными по факторной связи);

б) от 0,3 до 0,7 - есть связь между двумя факторами, но она считается достаточно слабой, чтобы ее учитывать в практических выводах, однако дополнение волновыми возмущениями может перевести в сильные связи;

в) выше 0,7 - имеется сильная связь между переменными факторами даже при не волновых биотехнических закономерностях.

По множеству крон измеренных берез по их высоте и мест их произрастания по углу местного склона выполнили статистическое моделирование идентификацией многочленной математической модели общего вида:

ϕ 1 = a 1 exp ( a 2 H к р а 3 ) ,

ϕ 2 = a 4 H к р а 5 exp ( − a 6 H к р а 7 ) ,

y i = b 1 i H к р b 2 i exp ( − b 3 i H к р b 4 i ) cos ( π Н к р / ( b 5 i + b 6 i H к р b 7 i ) − b 8 i ) ,

где φ - угол местного склона для места произрастания, град;

Н_кр - высота кроны дерева, м;

а₁…а₇, b₁…b₈ - параметры статистической модели, численные значения которых выявляются в программной среде при обработке конкретных массивов данных измерений (высота кроны и угол местного склона места произрастания) по всем березам из каждой популяции.

Исходные данные для моделирования приведены в таблице 2.

Таблица 2
Результаты измерений комля и места произрастания берез
№ березы	Высота кроны Н_кр, м	Угол φ, град	№ березы	Высота кроны Н_кр, м	Угол φ, град	№ березы	Высота кроны Н_кр, м	Угол φ, град
1	20,0	20	11	8,2	15	21	8,0	15
2	14,5	18	12	10,0	20	22	6,0	20
3	12,5	15	13	15,0	20	23	7,0	15
4	17,0	15	14	10,0	20	24	6,0	15
5	19,0	15	15	7,0	15	25	8,0	15
6	16,0	30	16	9,0	20	26	8,0	15
7	10,0	20	17	8,0	20	27	8,0	15
8	11,5	30	18	6,0	20	28	10,0	20
9	14,0	20	19	6,0	20	29	9,0	15
10	9,0	15	20	8,0	15	30	9,0	15
Примечание. Береза №6 резко отклоняется по значению угла местного склона, поэтому она была исключена из статистической выборки для моделирования.

Вначале получили тренд, то есть тенденцию (фиг.2), с детерминированными составляющими в виде формулы

ϕ = 16,43825 exp ( 8,94563 ⋅ 10 − 6 Н к р 3,05565 ) + + 6,84873 ⋅ 10 − 130 Н к р 168,44551 exp ( − 2,43554 Н к р 1,56371 )

Затем наращиванием этой статистической модели дополнительно получили две волновые составляющие (фиг.3 и фиг.4), а после их объединения получилась конкретная четырехчленная модель (фиг.5) вида:

φ=φ₁+φ₂+φ₃+φ₄,

ϕ 1 = 16,30066 exp ( 1,30789 ⋅ 10 − 7 Н к р 4,03577 ) ,

ϕ 2 = 3,61885 ⋅ 10 − 130 Н к р 168,42923 exp ( − 2,44759 Н к р 1,55864 ) ,

φ₃=A₁cos(πН_кр/р₁-4,14127),

A 1 = 1,49326 exp ( 1,87393 ⋅ 10 − 5 Н к р 3,76098 ) ,

p 1 = 1,61867 + 0,029031 Н к р 0,98269 ,

φ₄=A₂cos(πН_кр/p₂-4,68308),

A 2 = − 0,00055948 exp ( 6,02167 Н к р 0,14597 ) ,

p 2 = 0,0055948 + 0,23737 Н к р 0,48312 ) ,

где А₁, А₂ - амплитуды (половина) первого и второго колебательного возмущения угла местного склона на рост кроны дерева по высоте, град,

p₁, p₂ - полупериоды колебательного возмущения угла местного склона в зависимости от высоты кроны березы, м.

Для анализа наглядней запись в матричной форме как обобщенной волновой функции. В этом случае детерминированные составляющие являются амплитудами больших волн, у которых полупериод намного превышает диапазон (интервал) изменения влияющего фактора по оси абсцисс. Тогда получается, что две составляющие детерминированной модели имеют полупериоды колебательного возмущения намного более 20 м (максимальной высоты кроны из 30 берез).

В таблице 3 дана матричная запись всех четырех составляющих.

Таблица 3
Параметры общей математической модели
Номер i	Вейвлет y i = a 1 i x a 2 i exp ( − a 3 i x a 4 i ) cos ( π x / ( a 5 i + a 6 i x a 7 i ) − a 8 i )	Коэфф. коррел. r
амплитуда (половина) колебания	полупериод колебания	сдвиг
a_1i	a_2i	a_3i	a_4i	a_5i	a_6i	a_7i	a_8i
1	16,30066	0	-1,30789е-7	4,03577	0	0	0	0	0,9006
2	3,61885е-130	168,42923	2,44759	1,55864	0	0	0	0
3	1,49326	0	-1,87393е-5	3,76098	1,61867	0,029031	0,98269	4,14127
4	-0,00055948	0	-6,02167	0,14597	0,0055948	0,23737	0,48312	4,68308
Примечание. Функция для матричной записи параметров модели дана наверху таблицы.

Абсолютная погрешность (остатки) четырехчленной модели показывает, что в начале статистического ряда образовались три пары точек, противоположно расположенных относительно оси абсцисс, и они мешают дальнейшей идентификации волновой функции по остаткам. Этот факт указывает на то, что нужно повысить точность измерений высоты кроны от погрешности в ±0,5 м до погрешности ±0,1 м.

Анализ показывает, что по первой детерминированной составляющей с увеличением высоты кроны березы происходит экспоненциальный рост угла местного склона места ее произрастания. По таблице 2 этот процесс является кризисным (отрицательный знак перед параметром a_3i). При благоприятных условиях произрастания комли деревья стараются выравнивать склон до горизонтального уровня, формируя листовым аппаратом кроны поднятие комля над общим склоном оврага или холма.

Вторая детерминированная составляющая показывает стрессовое возбуждение комлевой части берез на ускоренный прирост угла местного склона на некотором интервале изменения высоты кроны.

Первая волна возмущения имеет рост по амплитуде колебания. На фиг.3 также видно, что при значительной высоте кроны график сильно раскачивается, что указывает на потерю влияния кроны на место произрастания на склоне оврага при выходе кроны за кромки оврага. Но при этом полупериод колебания нарастает, и процесс адаптации места произрастания в зависимости от высоты кроны успокаивается. В итоге частота колебательного возмущения уменьшается с ростом высоты кроны березы.

Вторая волна на фиг.4 показывает спокойное влияние высоты кроны на формирование места произрастания.

Из общей модели в данном примере можно заключить, что, осматривая кроны берез на склоне оврага или холма, вполне визуально можно оценить по их высоте качество березняка: чем выше высота кроны у каждой березы, тем качественнее формирование ею своего места произрастания.

Таким образом, предлагаемое техническое решение основано на результатах фундаментальных исследований взаимного влияния высоты кроны лесных деревьев, произрастающих как единая популяция и как микрогеотехническая система, десятилетиями на склоне оврага или холма.

Поэтому предлагаемый способ может быть применен в индикации не только лесного рельефа, но и фитоиндикации тех мест произрастания берез, расположенных на склонах оврагов и холмов, берегов малых рек и озер. Минимальное количество деревьев на одной пробной площади в виде полосы вдоль склона определяется возможностью идентификации биотехнических закономерностей и при этом количество учетных деревьев должно быть не менее 30 штук.

1. Способ анализа роста и развития высоты кроны березы, произрастающей на склоне, включающий выбор поперек склона пробной полосы леса с расположенными вдоль нее деревьями, отличающийся тем, что у каждой березы на пробной полосе вдоль склона измеряют высоту кроны и угол местного склона поперек общего склона у комля дерева, а для анализа роста и развития высоты кроны березы, произрастающей на склоне, по множеству измеренных параметров высоты кроны берез и угла местного склона места их произрастания статистическим моделированием выявляют взаимосвязь между высотой кроны березы и углом местного склона места ее произрастания.

2. Способ по п.1, отличающийся тем, что статистическое моделирование выполняют идентификацией многочленной однофакторной математической модели вида: , , , ,где φ - угол местного склона для места произрастания, град;φ₁ - первая детерминированная составляющая модели в виде устойчивого закона экспоненциального роста угла местного склона в зависимости от высоты кроны у множества измеренных берез, град;φ₂ - вторая детерминированная составляющая модели в виде устойчивого биотехнического закона, показывающего стрессовое возбуждение мест произрастания популяции берез по ускоренному увеличению угла местного склона на каком-то интервале изменения высоты кроны деревьев в популяции берез, град;y_i - волновые составляющие модели, показывающие колебательное возмущение места произрастания по углу местного склона в зависимости от изменения высоты кроны деревьев в популяции берез, град;i - номер волновой составляющей в виде асимметричного вейвлет-сигнала о колебательном взаимодействии кроны у популяции берез с местами их произрастания, шт.;m - общее количество волновых функций, зависящее от вычислительной возможности программной среды и погрешности измерений.Н_кр - высота кроны дерева, м;А_,…а₇, b₁…b₈ - параметры статистической модели, численные значения которых выявляются в программной среде при обработке конкретных массивов данных измерений высоты кроны и угла местного склона места произрастания по всем березам из каждой популяции.

Способ анализа кроны и места произрастания березы на склоне оврага

Патент 2525262