Способ определения модуля упругости материала

Способ определения модуля упругости материала

Иллюстрации

Показать все

Реферат

Изобретение относится к способам определения физико-механических свойств материалов путем приложения одиночного ударного усилия, а именно к способам определения модуля упругости материала и может быть использовано при решении целого ряда практических и теоретических задач, для выполнения которых необходима информация об упругих свойствах материалов и сред, а также об изменении данных свойств вследствие влияния различных факторов. Сказанное относится к таким процессам и явлениям, как получение новых материалов и изменение свойств существующих, контроль качества материалов при их производстве, разрушение материалов, уплотнение сыпучих материалов и сред (в строительной отрасли), обогащение и разделение сыпучих материалов по их свойствам и т.д.

Заявляемое изобретение относится к приоритетным направлениям развития науки и технологий «Технологии создания и обработки композиционных и керамических материалов» и «Технологии создания и обработки полимеров и эластомеров» [Алфавитно-предметный указатель к Международной патентной классификации по приоритетным направлениям развития науки и технологий / Ю.Г. Смирнов, Е.В. Скиданова, С.А. Краснов. - М.: ПАТЕНТ, 2008, - с.71, 75].

Существующие разработки не всегда позволяют качественно и быстро определять упругие свойства материалов, особенно в полевых условиях при отсутствии лабораторной базы и в подавляющем большинстве характеризуются низкой точностью. Поэтому проблема разработки эффективного мобильного способа определения упругих свойств материалов остается актуальной.

Определение упругих свойств материалов, в частности модуля упругости, может производиться путем статического сжатия или растяжения соответствующих образцов на прессах или разрывных машинах, например, в способе определения механических характеристик материала при испытании образца на растяжение [Сопротивление материалов / В.И. Феодосьев. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. - с.79].

Признаком аналога, совпадающим с существенным признаком заявляемого способа, является определение величины усилия при деформировании образца материала.

В ходе проведения таких испытаний определяются деформации при соответствующих нагрузках и рассчитывается модуль упругости материала.

Недостатком аналога в результате таких испытаний является ограниченная область применения и необходимость наличия сложного испытательного оборудования и соответствующих лабораторий, а также необходимость изготовления соответствующих образцов.

Более простыми и удобными являются ударные способы определения физико-механических свойств материалов. Согласно им по образцу исследуемого материала наносится удар индентором, например, стальным шариком, и по параметрам ударного взаимодействия судят о физико-механических свойствах материала, а именно упругости, пластичности, прочности, твердости и др. При этом в качестве параметров ударного взаимодействия используют высоту отскока индентора, скорости падения и отскока индентора, продолжительность удара и целый ряд других параметров.

В экспериментальной части близким аналогом к заявляемому способу определения модуля упругости материала является способ определения динамической твердости (а.с. СССР №1307295, кл. G01N 3/48, 30.04.1987).

Признаками аналога, совпадающими с существенными признаками заявляемого способа, являются: ударное воздействие по исследуемому объекту индентором; определение времени между первым и вторым соударениями индентора с исследуемым объектом, которое характеризует высоту отскока, и определение длительности первого соударения (времени удара).

Однако данный способ не позволяет на основе полученной информации оценить модуль упругости материала исследуемого объекта.

Известен способ контроля рабочих свойств акробатических дорожек (патент РФ №2020989, кл. G01N 3/52, 15.10.1994), который также близок к заявляемому в экспериментальной части.

Признаками аналога, совпадающими с существенными признаками заявляемого способа, являются: ударное воздействие по исследуемому объекту индентором; определение времени между первым и вторым соударениями индентора с исследуемым объектом, которое характеризует высоту отскока, и определение длительности первого соударения (времени удара).

Недостатком способа по патенту РФ №2020989 является: невозможность на основе полученной информации оценить модуль упругости материала исследуемого объекта. Определяется так называемая динамическая твердость конструкции акробатической дорожки.

Известен способ определения упругих свойств твердых материалов, согласно которому на поверхность образца исследуемого материала с заданной высоты сбрасывают индентор, например, стальной шарик, измеряют высоту отскока шарика и по высоте отскока судят об упругих свойствах исследуемого материала (Материалы Всесоюзного научно-исследовательского геологического института. Геофизика, сб. 12. - М.: Госгеолиздат, 1948, - с.62-71; а.с. СССР №59701, опубликовано 01.01.1941).

Признаками аналога, совпадающими с существенными признаками заявляемого способа, являются: ударное воздействие по исследуемому объекту индентором; определение высоты отскока индентора.

Недостатком способа является низкая достоверность, так как однозначно оценить упругие свойства исследуемого материала только по высоте отскока индентора практически невозможно. Объясняется это следующим.

В первую очередь высота отскока (или что то же самое при условии неучета аэродинамических сопротивлений движению при свободном отскоке и падении индентора время между первым и вторым соударениями индентора с образцом исследуемого материала) характеризует потери энергии удара на этапе контактного взаимодействия индентора с опорной поверхностью, которой является исследуемый образец. В частности, эти потери энергии могут быть объяснены возникающими в месте контакта пластическими деформациями, рассеянием энергии при упругих деформациях (внутреннее трение в материале), смятием или разрушением микронеровностей в зоне контакта и еще рядом факторов.

Таким образом, например, у материалов, имеющих близкие модули упругости, но различные пластические свойства, при ударе индентора возникают неодинаковые пластические деформации, сопровождаемые разными потерями энергии удара, а следовательно, высота отскока индентора оказывается различной. Из вышесказанного следует, что по высоте отскока индентора оценить упругие свойства материала можно только сложным косвенным способом, если известна взаимосвязь упругих свойств материала с факторами, характеризующими потери энергии на этапе контактного взаимодействия индентора с опорной поверхностью исследуемого образца. Поэтому для повышения достоверности способа необходимо использовать дополнительные параметры ударного взаимодействия, которые могут характеризовать упругие свойства материала более достоверно и точно. Таким параметром, например, может являться время удара.

Известен способ определения модуля нормальной упругости, использующий время удара, (а.с. №1497491, кл. G01N 3/30, 30.07.1989), в котором на образец исследуемого материала воздействуют свободно падающим индентором шарообразной формы с известными свойствами, измеряют время между первым и вторым соударениями индентора с образцом исследуемого материала, кроме этого, дополнительно измеряют диаметр отпечатка индентора и на основе полученной информации рассчитывают модуль упругости исследуемого материала по математической формуле.

Однако данный способ обладает существенными недостатками, основными из которых являются невысокая достоверность, ограниченная область применения и сложность практической реализации. Объясняется это следующим.

Дополнительный параметр, в качестве которого предлагается использовать диаметр отпечатка индентора, в первую очередь характеризует не упругие, а пластические свойства материала, так как исследуются остаточные (пластические) деформации, возникающие вследствие ударного взаимодействия индентора с опорной поверхностью образца исследуемого материала. Таким образом, используется сложная косвенная взаимосвязь искомого параметра (модуля упругости материала) с измеряемыми величинами - временем между первым и вторым соударениями индентора с образцом исследуемого материала и диаметром отпечатка индентора. Как уже отмечалось выше, у материалов, имеющих близкие модули упругости, но различные пластические свойства, при ударе индентора возникают неодинаковые пластические деформации и отпечатки индентора различные. Кроме того, пластические свойства материалов могут изменяться при различных видах обработки материалов. Например, при закалке стали существенно изменяется ее пластичность, хотя модуль упругости остается почти неизменным. Поэтому говорить о высокой достоверности данного способа на наш взгляд не всегда корректно.

Другим существенным недостатком прототипа является ограниченная область применения способа, так как он может быть реализован применительно к пластичным материалам. У хрупких материалов в зоне контакта возникают практически только упругие деформации, которые исчезают после снятия нагрузки. С другой стороны круг таких материалов достаточно широк, к ним относятся, например, каменные материалы (рудные и нерудные), чугуны, легированные закаленные стали и др.

Говоря о сложности практической реализации способа следует отметить, что измерение времени между первым и вторым соударениями индентора с образцом исследуемого материала и измерение диаметра отпечатка индентора можно осуществить только различными методами, требующими применения оборудования различного принципа действия, что ведет к усложнению практической реализации способа.

Наиболее точным и близким к предлагаемому способу является способ определения модуля материала (патент РФ №221221A, кл. G01N 3/32, 20.03.2006), взятый за прототип, в котором на образец исследуемого материала воздействуют свободно падающим индентором шарообразной формы с известными свойствами, измеряют время удара и время между первым и вторым соударениями индентора с образцом исследуемого материала (высоту отскока индентора).

Расчет модуля упругости выполняют с помощью расчетной механореологической упруго-вязкой модели с нелинейным упругим элементом с использованием экспериментально найденных значений времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала, для чего заменяют систему образец исследуемого материала - индентор на этапе контакта индентора с образцом исследуемого материала расчетной механореологической упруго-вязкой моделью с нелинейным упругим элементом, задают предварительное значение коэффициента жесткости упругого элемента модели, при заданном предварительном значении коэффициента жесткости упругого элемента модели рассчитывают время между первым и вторым соударениями модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента вязкости вязкого элемента модели, при котором значение времени между первым и вторым соударениями модели совпадает с измеренным значением времени между первым и вторым соударениями индентора с образцом исследуемого материала, при выбранном численном значении коэффициента вязкости вязкого элемента модели рассчитывают время удара модели, подбирая при этом численное значение коэффициента жесткости упругого элемента модели, а об искомом модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента модели, при котором время удара модели совпадает с измеренным временем удара индентора.

Однако данный способ обладает существенными недостатками, основным из которых является невысокая достоверность при исследовании пластичных материалов, и в связи с этим ограниченная область применения. Объясняется это следующим.

Основными механическими свойствами материала, влияющими на параметры ударного взаимодействия тел, являются упругость, пластичность, вязкость (диссипативные свойства), характеризующая потери энергии при упругом деформировании тела. К основным параметрам ударного взаимодействия тел относятся время и сила ударного взаимодействия тел, высота отскока тела после удара.

Основным недостатком способа является то, что в качестве расчетной механореологической модели используется упруго-вязкая модель. Данная модель имеет в своем составе упругий и вязкий элементы, что не позволяет учитывать влияние пластичности материала на параметры ударного взаимодействия тел. Проведенные исследования показали, что пластичность материала оказывает существенное влияние на динамику ударного процесса. Увеличение пластичности материала приводит к увеличению пластической деформации и времени удара и к снижению силы ударного взаимодействия и высоты отскока тела после удара.

Технический результат изобретения - повышение достоверности и расширение области применения способа определения модуля упругости материала за счет дополнительного измерения силы ударного взаимодействия индентора с образцом исследуемого материала и расчета модуля упругости исследуемого материала образца с помощью расчетной механореологической упруго-вязко-пластичной модели с использованием экспериментально найденных значений времени удара, времени между первым и вторым соударениями индентора с образцом исследуемого материала и силы ударного взаимодействия.

Технический результат достигается тем, что дополнительно измеряют максимальную величину силы ударного взаимодействия индентора с образцом исследуемого материала и устанавливают время, соответствующее максимальной величине силы ударного взаимодействия, расчет модуля упругости выполняют с помощью расчетной механореологической упруго-вязко-пластичной модели с использованием экспериментально найденного значения максимальной величины силы ударного взаимодействия индентора с образцом исследуемого материала и времени, соответствующего максимальной величине силы ударного взаимодействия, для чего заменяют систему образец исследуемого материала - индентор на этапе контакта индентора с образцом исследуемого материала расчетной механореологической упруго-вязко-пластичной моделью, задают предварительное значение коэффициента сдвига элемента сдвига упруго-пластического блока расчетной механореологической упруго-вязко-пластичной модели, при заданном предварительном значении коэффициента сдвига элемента сдвига расчетной механореологической упруго-вязко-пластичной модели рассчитывают время, соответствующее максимальному значению силы ударного взаимодействия индентора с образцом исследуемого материала, подбирая при этом численное значение коэффициента сдвига элемента сдвига расчетной механореологической упруго-вязко-пластичной модели, при котором значение времени, соответствующее максимальному значению силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели, совпадает с измеренным значением времени, соответствующим максимальному значению силы ударного взаимодействия индентора с образцом исследуемого материала, при выбранном численном значении коэффициента сдвига элемента сдвига расчетной механореологической упруго-вязко-пластичной модели рассчитывают максимальную величину силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента жесткости упругого элемента упруго-пластического блока расчетной механореологической упруго-вязко-пластичной модели, а об искомом модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента упруго-вязкого блока расчетной механореологической упруго-вязко-пластичной модели, при котором время удара, время между первым и вторым соударениями расчетной механореологической упруго-вязко-пластичной модели, время, соответствующее максимальному значению силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели, и максимальная величина силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели совпадут с измеренными значениями при ударе индентора с образцом исследуемого материала.

Анализ уровня техники показал наличие новизны в предложенной совокупности новых признаков, а именно:

- дополнительно измеряют максимальную величину силы ударного взаимодействия индентора с образцом исследуемого материала и устанавливают время, соответствующее максимальной величине силы ударного взаимодействия,

- расчет модуля упругости выполняют с помощью расчетной механореологической упруго-вязко-пластичной модели с использованием экспериментально найденных значений времени удара, времени между первым и вторым соударениями индентора с образцом исследуемого материала, времени, соответствующем максимальному значению силы ударного взаимодействия индентора и максимальной величины силы ударного взаимодействия индентора с образцом исследуемого материала,

- заменяют систему образец исследуемого материала - индентор на этапе контакта индентора с образцом исследуемого материала расчетной механореологической упруго-вязко-пластичной моделью;

- задают предварительное значение коэффициента сдвига элемента сдвига упруго-пластического блока расчетной механореологической упруго-вязко-пластичной модели, при заданном предварительном значении коэффициента сдвига элемента сдвига расчетной механореологической упруго-вязко пластичной модели рассчитывают время, соответствующее максимальному значению силы ударного взаимодействия индентора с образцом исследуемого материала, подбирая при этом численное значение коэффициента сдвига элемента сдвига расчетной механореологической упруго-вязко-пластичной модели, при котором значение времени, соответствующее максимальному значению силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели, совпадает с измеренным значением времени, соответствующим максимальному значению силы ударного взаимодействия индентора с образцом исследуемого материала

- при выбранном численном значении коэффициента сдвига элемента сдвига расчетной механореологической упруго-вязко-пластичной модели рассчитывают максимальную величину силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента жесткости упругого элемента упруго-пластического блока расчетной механореологической упруго-вязко-пластичной модели, а об искомом модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента упруго-вязкого блока расчетной механореологической упруго-вязко-пластичной модели, при котором время удара, время между первым и вторым соударениями расчетной механореологической упруго-вязко-пластичной модели, время, соответствующее максимальному значению силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели, и максимальная величина силы ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели совпадут с измеренными значениями при ударе индентора с образцом исследуемого материала.

Рассмотрим влияние отличительных признаков на достижение технического результата. Для повышения достоверности способа необходимо измерение дополнительных параметров ударного взаимодействия индентора с образцом исследуемого материала и более совершенное математическое описание рассматриваемого ударного процесса.

В заявляемом способе использование в качестве дополнительных параметров измерения максимальной величины силы ударного взаимодействия индентора с образцом исследуемого материала и времени, измеренного от начала удара до момента, соответствующего максимальной величине силы ударного взаимодействия, позволяет качественно учесть влияние пластичности материала на динамические параметры ударного взаимодействия расчетной механореологической упруго-вязко-пластичной модели. Как показали проведенные исследования, на указанные дополнительные параметры ударного процесса в первую очередь оказывает влияние элемент сдвига расчетной механореологической упруго-вязко-пластичной модели. С другой стороны этот элемент непосредственно связан с пластичностью материала и обеспечивает адекватность модели реальному материалу по пластическим свойствам.

Таким образом, данная операция позволяет повысить достоверность способа и расширить его область применения и является его неотъемлемой частью.

Для моделирования процесса на компьютере и осуществления расчетов необходима разработка и использование математической модели ударного взаимодействия индентора с исследуемым образцом материала. Необходимость моделирования рассматриваемого процесса объясняется тем, что модуль упругости материала нельзя измерить непосредственно в ходе эксперимента. Это параметр, к которому можно прийти только расчетным путем на основе исходных данных о динамике ударного взаимодействия индентора с исследуемым образцом материала. Разработка математической модели процесса потребовала проведения дополнительных теоретических исследований.

Используемая расчетная модель должна обеспечивать адекватность динамики движения и взаимодействия индентора с образцом исследуемого материала при математическом моделировании процесса. Критериями адекватности согласно заявляемому способу были приняты четыре параметра ударного процесса: время между первым и вторым соударениями индентора с образцом исследуемого материала, время удара, максимальная величина силы ударного взаимодействия индентора с образцом исследуемого материала и время от начала удара до момента, соответствующего максимальной величине силы ударного взаимодействия. Параметры ударного процесса, связанные с силой ударного взаимодействия, характеризуют новизну способа.

Время между первым и вторым соударениями индентора с образцом исследуемого материала характеризует высоту отскока индентора, если не принимать во внимание силы аэродинамических сопротивлений, возникающих при движении индентора в воздухе. Применительно к рассматриваемому случаю это вполне допустимо, так как при незначительных скоростях движения силы аэродинамических сопротивлений несоизмеримо малы по сравнению с собственным весом, например, стального индентора. Высота отскока индентора характеризует потери энергии при ударе на этапе контактного взаимодействия индентора с опорной поверхностью, которой является образец исследуемого материала. Эти потери энергии возникают при упругой деформации материала (внутреннее трение в материале). Для того, чтобы обеспечить адекватность расчетной модели по высоте отскока, т.е. по потерям энергии, она должна иметь соответствующий элемент. Для этой цели нами использован широко распространенный вязкий элемент (Сопротивление материалов / Под ред. Писаренко Г.С. - Киев: Вища шк., 1986. - с.604; Лапшин В.Л., Байбородин Б.А. Аналитическое моделирование процесса разделения руд на вибродеке. - Иркутск: Изд-во Иркутск, гос. техн. ун-та, 1997. - с.24). Изменяя численное значение коэффициента вязкости вязкого элемента расчетной модели, можно регулировать потери энергии при деформации и, следовательно, ее высоту отскока.

Время удара связано с упругими свойствами взаимодействующих тел (сферическое тело-плоскость). Задача о сдавливании сферических тел была решена Г. Герцем еще в 1881 г (Тимошенко С.П. Теория упругости. - Л. - М.: ОМТИ, 1937. - с.451). Им был предложен нелинейный упругий элемент, который позволяет рассчитать деформации при взаимодействии сферических тел в зависимости от их модулей упругости. Последующие практические исследования подтвердили достоверность предложенной модели. Поэтому в качестве упругого элемента упруго-вязкого блока расчетной механореологической упруго-вязко-пластичной модели нами выбран нелинейный упругий элемент Г. Герца. Он позволяет обеспечить адекватность модели по времени удара путем подбора численного значения коэффициента жесткости упругого элемента. При известном значении коэффициента жесткости упругого элемента расчетной упруго-вязкой модели для расчета модуля упругости исследуемого материала образца используется расчетная формула.

Отличительным признаком расчетной механореологической модели является упруго-пластический блок, расположенный последовательно с упруго-вязким блоком модели. Именно упруго-пластический блок позволяет качественно учесть пластичность материала при деформировании материала. Обеспечивая адекватность модели реальному процессу по силе ударного взаимодействия мы устраняем влияние пластичности материала на оценку его упругих свойств и повышаем достоверность способа.

Таким образом, использование для математического описания процесса ударного взаимодействия индентора с образцом исследуемого материала более совершенной расчетной механореологической упруго-вязко-пластичной модели, оценка пластичности материала по максимальной величине силы ударного взаимодействия индентора с образцом исследуемого материала и времени, соответствующем максимальной величине силы ударного взаимодействия, с помощью упруго-пластического блока расчетной механореологической упруго-вязко-пластичной модели являются неотъемлемыми операциями способа, позволяющими на основе исходных экспериментальных данных рассчитать искомый модуль упругости исследуемого материала образца с более высокой достоверностью.

Следует отметить, измерение дополнительных параметров не приводит к усложнению практической реализации способа. Измерение можно осуществить одним и тем же методом, не требующим применения оборудования различного принципа действия, например, с помощью датчика ускорения (акселерометра), который закрепляется на инденторе. Ускорение пропорционально силе ударного взаимодействия и позволяет осуществить измерение всех параметров ударного процесса.

Дополнительный поиск известных решений с признаками, совпадающими с отличительными от прототипа признаками заявляемого способа, не выявил влияния существенных признаков на достижение поставленного технического результата. Поэтому заявляемое изобретение соответствует критерию "изобретательский уровень".

Сущность изобретения поясняется чертежами, где

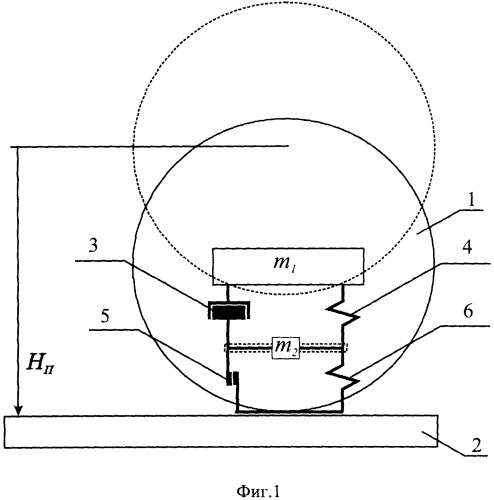
на фиг.1 изображена схема расчетной механореологической упруго-вязко-пластичной модели;

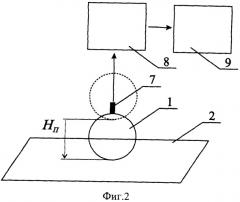
на фиг.2 - схема экспериментальной установки;

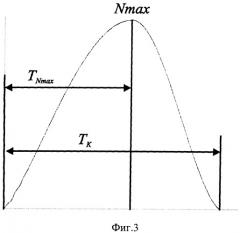
на фиг.3 - график изменения силы ударного взаимодействия.

На чертежах приняты следующие обозначения:

m₁ - масса индентора (тела);

m₂ - масса вспомогательного инерционного элемента;

T_K - продолжительность ударного взаимодействия (время удара);

N_max - максимальная величина силы ударного взаимодействия;

T_Nmax - время, соответствующее максимальному значению силы ударного взаимодействия;

1 - сферический индентор;

2 - образец исследуемого материала;

3 - коэффициент вязкости C вязкого элемента упруго-вязкого блока модели;

4 - коэффициент жесткости упругого элемента K₁ упруго-вязкого блока модели;

5 - коэффициент сдвига f₂ упруго-пластического блока модели или коэффициент податливости материала;

6 - коэффициент жесткости K₂ упругого элемента упруго-пластического блока модели;

7 - датчик ускорения (типа АР-2019);

8 - анализатор спектра (типа A17-U2);

9 - компьютер с программным обеспечением.

Заявляемый способ осуществляется следующим образом. В процессе эксперимента свободно падающим индентором шарообразной формы с известными свойствами наносится удар по образцу исследуемого материала и фиксируются параметры ударного взаимодействия: время удара, время между первым и вторым соударениями индентора с образцом исследуемого материала (высота отскока), максимальная величина силы ударного взаимодействия индентора с образцом исследуемого материала и время, соответствующее максимальной величине силы ударного взаимодействия. Для этого с помощью измерительного оборудования и соответствующего программного обеспечения записывается график изменения силы ударного взаимодействия (фиг.3) при двух последовательных ударах (второй удар происходит после отскока при первом ударе). График строится в масштабе в осях время (t) - ускорение (a), из него определяются все необходимые экспериментальные данные. Сила ударного взаимодействия рассчитывается F=m₁ a. Далее выполняется расчет с помощью разработанной программы. Для этого используется расчетная механореологическая упруго-вязко-пластичная модель.

Рассмотрим расчетную механореологическую упруго-вязко-пластичную модель, схема которой представлена на фиг.1. Данная модель позволяет описать динамику процесса ударного взаимодействия индентора шарообразной формы с образцом исследуемого материала. Дифференциальное уравнение движения центра тяжести индентора шарообразной формы на этапе ударного взаимодействия имеют вид:

m 1 y • • 1 + C 1 ( y • 1 − y • 2 ) ( y 1 − y 2 ) + K 1 ( y 1 − y 2 ) 3 / 2 = − m 1 g ;         ( 1 )

m 1 y • • 2 + K 2 y 2 3 / 2 + f 2 y 2 + C 1 ( y • 2 − y • 1 ) ( y 2 − y 1 ) + K 1 ( y 2 − y 1 ) 3 / 2 = − m 2 g ;         ( 2 )

где y₁,y₂,y₁,y₂ - перемещение и скорость масс m₁ и m₂;

K₁ - коэффициент жесткости упругого элемента упруго-вязкого блока модели;

C - коэффициент вязкости вязкого элемента упруго-вязкого блока модели;

K₂ - коэффициент жесткости упругого элемента упруго-пластического блока модели;

f₂ - коэффициент сдвига упруго-пластического блока модели или коэффициент податливости материала.

Сила ударного взаимодействия определяется:

N 1 = C ( y • 1 − y • 2 ) ( y 1 − y 2 ) + K 1 ( y 1 − y 2 ) 3 / 2 .       ( 3 )

Модель включает в себя два последовательных блока: упруго-вязкий блок K₁-C и упруго-пластический блок K₂-f₂. Блок K₁-C описывает упругие деформации системы и учитывает возникающие при этом потери энергии с помощью демпфера, сопротивление в котором принимается пропорциональным скорости и величине упругой деформации. Блок K₂-f₂ описывает пластические деформации и также учитывает возникающие при этом потери энергии.

Вся масса индентора сосредоточена в инерционном элементе m₁, масса элемента m₂ ничтожно мала (m₂→0) и не оказывает заметного влияние на динамику движения модели. Она введена для удобства математического описания системы с помощью двух дифференциальных уравнений второго порядка.

Функционирование упруго-вязко-пластичной модели осуществляется следующим образом. На этапе нагружения работают оба блока модели, описывающие упругие и пластические (остаточные) деформации. Когда рост деформации прекращается и скорость деформации становится равной нулю, сила ударного взаимодействия достигает максимального значения и наступает этап разгрузки модели. На данном этапе в работу вступает только упруго-вязкий блок, описывающий исчезновение только упругих деформаций. При этом упруго-пластический блок остается в деформированном состоянии, так как характеризует пластические деформации материала.

На базе математической модели была разработана специальная исследовательская программа. Решение системы уравнений (1)-(2) осуществлялось численным методом Рунге-Кутта.

Коэффициент жесткости упругого элемента упруго-вязкого блока расчетной механореолгической упруго-вязко-пластичной модели K₁ связан со свойствами и параметрами индентора и свойствами исследуемого образца материала и рассчитывается по формуле (Тимошенко С.П. Теория упругости. - Л. - М.: ОМТИ, 1937. - с.451):

K 1 = 4 3 π R 1 R 2 ( R 1 + R 2 ) [ 1 − μ 1 2 π E 1 + 1 − μ 2 2 π E 2 ] 2 ,             ( 3 )

где R₁, R₂ - радиусы кривизны индентора шарообразной формы и поверхности образца исследуемого материала;

E₁, Е₂ - модули упругости (модули Юнга) соответственно материала индентора и исследуемого образца;

µ₁, µ₂ - коэффициенты Пуассона соответственно материала индентора и исследуемого образца.

Последовательность определения модуля упругости материала исследуемого образца выглядит следующим образом.

Задаются исходные данные расчетной механореолгической упруго-вязко-пластичной модели m₁, m₂, R₁, R₂, E₁, Е₂, µ₁, µ₂, С, K₂, f и рассчитывается начальная скорость индентора в момент удара (Н_П - исходная высота падения индентора; g - ускорение свободного падения). Для материала индентора параметры E₁, µ₁ являются известными. Если поверхность исследуемого образца материала является плоской, то вышеприведенные формулы так же применимы. В этом случае достаточно принять радиус кривизны поверхности исследуемого образца R₂ намного большим радиуса кривизны индентора R₁ (например R₂=1000 м). Погрешность расчета в этом случае ничтожна мала. Для C, Е₂, K₂, f принимаются ориентировочные значения (например C=0, E₂=E₁, K₂=K₁, f=50). Коэффициент Пуассона материала исследуемого образца, как показали предварительные расчеты, оказывает очень незначительное влияние на конечный результат, даже если его варьировать в широких пределах (например, µ₂=