Способ определения вероятности ошибки на бит по флуктуациям фазы информационных сигналов

Способ определения вероятности ошибки на бит по флуктуациям фазы информационных сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области электрорадиотехники, а именно к технике радиосвязи, и может быть использовано в системах передачи данных, при работе в заданной частотной полосе без введения избыточности, для определения качества канала связи.

Для обеспечения стабильной работы системы передачи данных необходимо осуществлять контроль качества используемого канала связи. Критерием качества канала в цифровых системах связи является вероятность ошибки на бит.

Известен способ измерения вероятности ошибки на бит, описанный в патенте США №4100531. Он заключается в том, что на передающей стороне формируют тестовый сигнал, представляющий собой модулированный псевдослучайный сигнал. Во время прохождения через канал тестовый сигнал изменяется за счет свойств канала, а также к нему добавляется случайный шум. На приемной стороне осуществляют прием сигнала и его демодуляцию, а затем реализуют побитное сравнение принятой последовательности бит с эталонной последовательностью. Несовпадение сравниваемых бит считают ошибкой. Оценку вероятности ошибки определяют как отношение количества зарегистрированных ошибок к длине последовательности.

Данный способ требует прерывания передачи полезной информации на время, необходимое для передачи тестового сигнала. В реальном канале связи его характеристики меняются во времени, и при этом изменяется вероятность ошибки, поэтому эту операцию проводят периодически через определенные промежутки времени. Производимые для этой цели прерывания передачи сообщений усложняют возможность применить этот способ в системах непрерывной передачи данных, а также непосредственно снижают информационную скорость передачи сообщений.

Наиболее близкой к предлагаемому техническому решению, обеспечивающей получение оценки качества канала в условиях непрерывной и безызбыточной передачи данных является система, описанная в патенте РФ №2451407, год регистрации патента 2012 г. Оценка вероятности ошибки определяется с помощью анализа принимаемого полезного сигнала и восстановления плотности разности фаз.

В этой системе на передающей стороне формируют сигнал в модуляторе на основе полезной информации, которую необходимо передать. После модулятора передают сформированный сигнал по каналу связи. Далее, после прохождения сигналом канала, осуществляют его прием на приемной стороне, при этом на приемной стороне принятый сигнал подают параллельно на демодулятор и блок оценки, в котором осуществляют оценку вероятности ошибки на бит, формируя выборочную плотность распределения разности фаз между двумя соседними посылками, на основе доступных для измерения выборочных плотностей распределения разности фаз между двумя сегментами элементарной посылки и фазовой поправки, которая реализуется через преобразователь Фурье, а искомая оценка вероятности ошибки на бит определяется путем интегрирования вычисленной плотности разности фаз между двумя элементарными посылками в заданных пределах, предоставляя постоянно корректируемую оценку качества канала связи.

Для обеспечения возможности использования оценки вероятности ошибки на бит таким способом необходимо, чтобы часть разрешенной частотной полосы оставалась свободной, т.е. не использовалась для передачи.

Таким образом, данный способ не позволяет достичь максимально возможных скоростей передачи сообщений по каналу связи.

Целью настоящего изобретения является обеспечение получения оценки качества канала связи в процессе работы системы передачи данных, не прерывая при этом полезную информацию.

Поставленная цель достигается тем, что способ определения вероятности ошибки на бит по флуктуациям фазы информационных сигналов состоит в том, что на передающей стороне формируют сигнал в модуляторе на основе полезной информации, которую необходимо передать, а после модулятора передают сформированный сигнал по каналу связи, причем после прохождения сигналом канала связи осуществляют его прием на приемной стороне и подают принятый сигнал на демодулятор и блок оценки, в котором осуществляют оценку вероятности ошибки на бит, при этом вычисленные разности фаз передают с демодулятора в блок накопления, в котором производят их накопление, и передают накопленный массив в блок решения уравнения, в котором численным методом, например методом золотого сечения, решают уравнение

∑ i = 1 N cos ( Δ ϕ i ) t h ( D cos ( Δ ϕ i ) ) − N I 1 ( D ) I 0 ( D ) = 0 ,

где Δφ_i - разница фаз между i и i+1 посылкой, N - длина массива, I₀(D) - функция Бесселя нулевого порядка, I₁(D) - функция Бесселя первого порядка, D - искомое решение полученного уравнения, D ^ - оценка величины D, после решения которого полученную оценку D ^ передают в блок восстановления плотности, в котором восстанавливают плотность распределения разности фаз между соседними посылками W ^ 0 ( Δ ϕ ) и используют для этого выражение W ^ 0 ( Δ ϕ ) = 1 2 π I 0 ( D ^ ) e D ^ cos ( Δ ϕ ) , которую далее передают в блок интегрирования, в котором реализуют интегрирование данной плотности в соответствии с заданными пределами интегрирования, получая, таким образом, искомую оценку вероятности ошибки на бит.

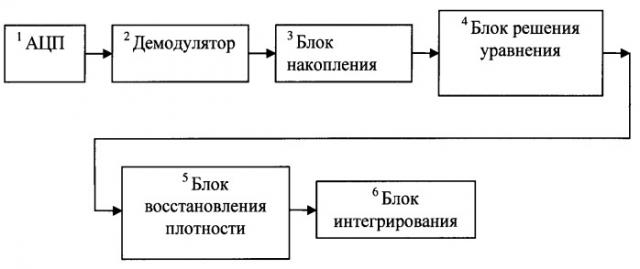
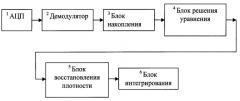
Структурная схема предложенного способа приведена на чертеже.

Поставленная задача решается следующим образом.

Предположим, что на длительности элементарной посылки фаза сигнала не испытывает разрывов, а входной поток данных является двоичным биноминальным случайным процессом, то есть начальная фаза принимает разрешенные значения (позиции) на выходе модулятора с равной вероятностью.

После прохождения канала связи разность начальных фаз между двумя соседними посылками будет отличаться от известного значения, то есть будут наблюдаться ее флуктуации. На основе данных разностей фаз, доступных для измерения, можно сформировать плотность распределения разности фаз для посылок заданной длительности и оценить искомую вероятность ошибки на бит.

Плотность распределения вероятности начальной фазы смеси сигнала и шума (при условии, что начальная фаза сигнала постоянна и равна нулю) достаточно хорошо описывается нормальным угловым законом распределения [1, 3]:

W ( ϕ ) = 1 2 π e − 1 2 h 2 [ 1 + 2 π ⋅ h ⋅ cos ( ϕ ) Φ ( h ⋅ cos ( ϕ ) ) e 1 2 h 2 cos 2 ( ϕ ) ] ,

-π≤φ≤π,

где Φ ( x ) = 1 2 π ∫ − ∞ x e − 1 2 x 2 d x - интеграл вероятности, h²-отношение сигнал/помеха.

Плотность распределения разностей фаз между двумя соседними посылками описывается распределением Мизеса [1, 3]:

W 0 ( ϕ ) = 1 2 π I 0 ( D ) e D cos ( Δ ϕ ) ,

где I₀(D) - функция Бесселя нулевого порядка, интеграл вероятности, D=2h².

Если разность фаз между двумя соседними посылками сигнала с равной вероятностью принимает значения 0 и π, то плотность вероятности разностей фаз такого сигнала может быть описана смесью плотностей:

W 0, π ( Δ ϕ ) = 1 2 W 0 ( Δ ϕ ) + 1 2 W 0 ( Δ ϕ + π ) , -π≤φ≤π.

Обычно в такой ситуации сначала предпринимается попытка классификации выборки измеренных разностей фаз и разделения ее на две подвыборки, которые состоят из случайных величин, распределенных по разным законам. Однако данная операция является неточной и в образованных подвыборках всегда содержатся случайные величины, классифицированные неверно. Поэтому в данной работе предлагается рассматривать всю выборку разностей фаз целиком.

Поэтому данный подход позволяет избежать процедуры классификации.

Если для передачи данных используется двухпозиционная относительная фазовая модуляция, то можно сформировать выборку разностей фаз на некотором временном интервале. Используя в качестве модели теоретическую плотность распределения разностей фаз W_0,π(Δφ) на основе полученной выборки можно оценить параметры распределения. Воспользуемся методом максимального правдоподобия для оценки неизвестного параметра распределения D [2]. Для этого необходимо найти аргумент, при котором функция правдоподобия достигает максимума. Данный аргумент будет являться состоятельной и эффективной оценкой искомого параметра. Функция правдоподобия имеет следующий вид:

L ( D ) ∏ i = 1 N W 0, π ( Δ ϕ i , D ) ,

где Δφ_i - измеренная разность фаз между i и (i+1) посылками, N -объем выборки.

Как известно, для нахождения точек максимума функции L(D) необходимо решить уравнение

∂ L ( D ) ∂ D = 0

∂ ( ∏ i = 1 N ( 1 2 1 2 π I 0 ( D ) e D cos ( Δ ϕ i ) + 1 2 1 2 π I 0 ( D ) e D cos ( Δ ϕ i + π ) ) ) ∂ D =             = ∂ ( 1 ( 2 π I 0 ( D ) ) N ∏ i = 1 N ( c h ( D cos ( Δ ϕ ) ) ) ) ∂ D = 0

Выполнив операцию дифференцирования, получим:

∏ i = 1 N ( c h ( D cos ( Δ ϕ i ) ) ) ( 2 π ) N ( I 0 ( D ) ) N ( ∑ i = 1 N cos ( Δ ϕ i ) t h ( D cos ( Δ ϕ i ) ) − N I 1 ( D ) I 0 ( D ) ) = 0

Оценка может быть определена путем решения данного нелинейного уравнения. В замкнутом виде решение этого уравнения найти не удается. Однако использование численных методов решения позволяет определить корень уравнения с требуемой точностью при незначительных вычислительных затратах, что позволяет использовать этот алгоритм в системах реального времени. Стоит отметить, что быстродействие современных систем обработки сигналов позволяет широко использовать численные методы статистического анализа.

Например, можно воспользоваться методом золотого сечения для оценивания величины D.

Пусть D ^ - это оценка решения полученного уравнения. Найденная оценка может быть использована для восстановления плотности W₀(Δφ). Таким образом, оценка W ^ 0 ( Δ ϕ ) определяется следующим образом:

W ^ 0 ( Δ ϕ ) = 1 2 π I 0 ( D ^ ) e D ^ cos ( Δ ϕ ) ,

-π≤Δφ≤π

Тогда оценка вероятности ошибки на бит определяется выражением:

P ^ = 1 − ∫ − π 2 π 2 W ^ 0 ( Δ ϕ ) d Δ ϕ

Аналогичные выражения могут быть получены и применены для формирования оценки вероятности ошибки на бит для всех возможных режимов (кратностей модуляции), включая используемый в данный момент.

Этот способ может быть применен как для синхронного, так и для асинхронного режима передачи данных.

Отличительной особенностью описанного способа является возможность формировать оценку вероятности ошибки на бит при использовании сигналов с относительной фазовой модуляцией в условиях плотного частотного заполнения канала связи без введения избыточности. Наличие такой оценки позволяет отказаться от применения тестовых сигналов для оценивания качества канала связи. При этом разрешенная частотная полоса используется максимально эффективно, а скорость передачи данных повышается. Кроме того, данная оценка формируется за достаточно короткий интервал времени, что позволяет адаптивным системам связи своевременно реагировать на изменение качества канала связи и изменять свои параметры заранее, обеспечивая при этом передачу данных без обрыва канала связи и максимально возможную в текущей сигнально-помеховой обстановке информационную скорость.

При этом данный способ позволяет использовать для передачи данных всю выделенную частотную полосу, позволяя таким образом увеличить информационную скорость в два раза по сравнению с прототипом.

Описываемый способ работает следующим образом.

Принимаемый сигнал подают на аналогово-цифровой преобразователь 1, в котором получают отсчеты сигнала, которые затем поступают в демодулятор 2, где производят вычисление разностей фаз между соседними посылками принимаемого сигнала. Далее вычисленные разности фаз подают на блок накопления 3, в котором производят накопление вычисленных разностей фаз. Затем накопленный массив разностей фаз передают в блок решения уравнения 4, в котором численным методом, например методом золотого сечения, решают уравнение ∑ i = 1 N cos ( Δ ϕ i ) t h ( D cos ( Δ ϕ i ) ) − N I 1 ( D ) I 0 ( D ) = 0 ,

где Δφ_i - разница фаз между i и i+1 посылкой, N - длина массива, I₀(D) - функция Бесселя нулевого порядка, I₁(D) - функция Бесселя первого порядка, D - искомое решение полученного уравнения, D ^ - оценка величины D. После этого полученную оценку D ^ передают в блок восстановления плотности 5, в котором восстанавливают плотность распределения разности фаз между соседними посылками W ^ 0 ( Δ ϕ ) и используют для этого выражение W ^ 0 ( Δ ϕ ) = 1 2 π I 0 ( D ^ ) e D ^ cos ( Δ ϕ ) . Далее восстановленную плотность распределения передают в блок интегрирования 6, в котором реализуют интегрирование данной плотности в соответствии с заданными пределами интегрирования, получая, таким образом, искомую оценку вероятности ошибки на бит.

Литература

1. В.И.Тихонов. Статистическая радиотехника. М.: Советское радио, 1966, 677 стр.

2. И.Н.Коваленко. А.А.Филиппова. Теория вероятностей и математическая статистика. М.: Высшая школа, 1973, 367 стр.

3. К.Мардиа. Статистический анализ угловых наблюдений. М.: Наука, 1978, 240 стр.

Способ определения вероятности ошибки на бит по параллельным флуктуациям фазы информационных сигналов, заключающийся в том, что на передающей стороне формируют сигнал в модуляторе на основе полезной информации, которую необходимо передать, а после модулятора передают сформированный сигнал по каналу связи, причем после прохождения сигналом канала связи осуществляют его прием на приемной стороне и подают принятый сигнал на демодулятор и блок оценки, в котором осуществляют оценку вероятности ошибки на бит, отличающийся тем, что вычисленные разности фаз передают с демодулятора в блок накопления, в котором производят их накопление, и передают накопленный массив в блок решения уравнения, в котором численным методом, например методом золотого сечения, решают уравнение ∑ i = 1 N cos ( Δ ϕ i ) t h ( D cos ( Δ ϕ i ) ) − N I 1 ( D ) I 0 ( D ) = 0 , где Δφ_i - разница фаз между i и i+1 посылкой, N - длина массива, I₀(D) - функция Бесселя нулевого порядка, I₁(D) - функция Бесселя первого порядка, D - искомое решение полученного уравнения, D ^ - оценка величины D, после решения которого полученную оценку D ^ передают в блок восстановления плотности, в котором восстанавливают плотность распределения разности фаз между соседними посылками W ^ 0 (Δφ) и используют для этого выражение W ^ 0 (Δφ) = 1 2 π Ι 0 ( D ^ ) e D ^ C O S ( Δ ϕ ) , которую далее передают в блок интегрирования, в котором реализуют интегрирование данной плотности в соответствии с заданными пределами интегрирования, получая, таким образом, искомую оценку вероятности ошибки на бит.