Способ центробежной порометрии

Способ центробежной порометрии

Иллюстрации

Показать все

Реферат

Изобретение относится к методам исследования пористой структуры разнообразных природных и искусственных пористых объектов и может быть использовано в тех областях науки и техники, где они исследуются или применяются.

Известен центробежный метод нахождения функции распределения пор по размерам в пористых объектах [Ксенжек О.С., Калиновский Е.А., Петрова С.А., Литвинова В.И. Центробежный метод нахождения функции распределения пор по размерам в пористых средах. //Журнал физической химии, 1967, ХLI, №7, с.1602-1607].

Он основан на естественном заполнении пористого объекта смачивающей жидкостью с последующим удалением ее центрифугированием при наборе возрастающих значений центробежного ускорения (частоты центрифугирования). На каждом из этих значений измеряется объем жидкости в исследуемом образце. Для получения кривой распределения объема пор по их радиусам значения центробежного ускорения необходимо перевести в радиусы пор. В рамках модели пористого пространства в виде параллельных не пересекающихся цилиндров разных радиусов, минимальный радиус пор, из которых вытеснена жидкость, определяется уравнением

r = 2 ⋅ σ ⋅ cos θ d ⋅ ρ ⋅ ( 2 π n ) 2 R                                                                                 (1)

где σ - коэффициент поверхностного натяжения рабочей жидкости,

ρ - ее плотность,

θ - краевой угол смачивания,

d- толщина образца вдоль направления действия центробежной силы,

n - частота вращения ротора центрифуги (об/мин),

R - радиус центрифугирования.

Распределение радиусов пор получают графическим дифференцированием экспериментальной порограммы - кривой распределения объема пор по их радиусам.

Несмотря на ряд преимуществ центробежного метода по сравнению с другими методами порометрии, он не получил практического применения в силу ряда нерешенных проблем его технической реализации. Избранный авторами метод динамического контроля вытеснения жидкости может использоваться при одномоментном исследовании только одного образца и не может обеспечить точности измерения, необходимой для порометрии объектов с малыми объемами пор (исследовались объекты с объемной пористостью 50-70%). Еще одним недостатком, ограничивавшим возможность расширения измеряемого диапазона пор, было использование рабочих жидкостей, которые с увеличением общего времени центрифугирования, будут давать ошибку, обусловленную их неконтролируемым испарением.

Прототипом предлагаемого изобретения служит метод центробежной порометрии, примененный для исследования пористости костной ткани [Луньков А.Е., Куликова Л.Н. //Применение центробежной порометрии для морфометрии костной ткани//, Медицинская физика, 2011, №1, стр.69-74], в котором определение количества жидкости в образцах производится путем взвешивания их на аналитических весах. Малая погрешность взвешивания (±0,1 мг) обеспечивает получение характеристик пористости объектов с объемной пористостью менее 10% в диапазоне радиусов пор от 0,1 до 100 мкм. Погрешность, связанная с испарением рабочей жидкости в процессе центрифугирования, устраняется за счет использования в качестве рабочей жидкости вакуумного масла ВМ-6, имеющего давление насыщенных паров порядка 10^-6 мм рт.ст.

Недостатком прототипа является возможное расхождение экспериментально полученного и реального распределения пор по размерам, которое может возникать для большого числа объектов, пористая структура которых соответствует модели «полостей и горл», то есть локальных внутренних полостей, соединяемых цепочками канальцев (горл) меньшего диаметра.

При любом типе пористой структуры возможность центробежного вытеснения жидкости из цепочки пор переменного сечения ограничивается сечением минимального диаметра. В силу этого при пористой структуре типа «полостей и горл» получается распределение объема полостей по размерам горл, так как возможность освобождения полости определяется радиусами горл, всегда меньшими линейных размеров полостей. При этом имеет место еще одно условие центробежного вытеснения жидкости из каждой случайно выбранной полости, получившее название «перколяционной вероятности».

В теории перколяции (просачивания) [Тарасевич Ю.Ю. //Перколяция: теория, приложения, алгоритмы// 2002, М., изд. «Едиториал УРСС»; Фенелонов В.Б. //Введение в физическую химию формирования супрамолекулярной структуры адсорбентов и катализаторов// 2004, Новосибирск, изд. СО РАН.] установлено, что возможность удаления жидкости из полостей определяется не только радиусами соединенных с ними горл, но и вероятностью того, что эти потенциально проницаемые (при данном центробежном ускорении) горла входят в непрерывную цепочку, соединяющую эти полости с внешней поверхностью пористого тела. Эта вероятность равна N/N₀, где N₀ - общее число потенциально проницаемых горл (радиусы которых больше r соотношения (1)), а N - число этих горл, входящих в цепочки вытеснения жидкости из полостей. Произведение среднего числа горл одной полости Z на эту вероятность, то есть Z в = Z ⋅ N N в называют средним координационным числом перколяционной решетки, состоящей из полостей, связанных проводящими горлами. Перколяционной вероятностью называют отношение числа полостей М, из которых удалена жидкости, к общему числу полостей М₀.

Результатом теории перколяции, имеющим важнейшее практическое значение, является установление общей для любого типа решетки пористости зависимости перколяционной вероятности от Z_в. Согласно этой зависимости, для объемных решеток перколяционная вероятность (М/М₀) меняется от 0 до 1 при изменении Z_в от 1,5 до 2,7. То есть, вытеснение жидкости начинается, когда на каждую полость приходится в среднем 1,5 горла, через которые возможно удаление жидкости при данном центробежном ускорении. При достижении значения Z_в=2,7 все поры освобождены и дальнейшее увеличении центробежного ускорения и, соответственно N₀ не дает никакой информации о горлах меньших диаметров.

Применительно к центробежной порометриии это означает, что от начала до окончания процесса вытеснения жидкости центробежное ускорение и, следовательно, определяемые экспериментально радиусы пор могут измениться незначительно. В силу этого по порограмме будет определяться лишь часть реального диапазона радиусов горл, если они меняются в более широких пределах.

Нами предлагается способ устранения этого недостатка и повышения точности определения спектра радиусов пор. Поставленная задача решается на основе неразрушающего характера центробежной порометрии путем проведения повторного снятия порограмм одного и того же образца после уменьшения его толщины-d.

Сущность предлагаемого способа обосновывается следующими соображениями.

При каждом значении центробежного ускорения перколяционная вероятность может определяться как отношение объема вытесненной жидкости к общему объему пор (или как отношение разности общего объема пор и объема еще не вытесненной жидкости к общему объему пор). Изменение перколяционной вероятности возможно за счет изменения толщины образца, поскольку с ее уменьшением каждая полость приближается к внешней поверхности и увеличивается вероятность образования из потенциально проницаемых горл проводящей цепочки связи с этой полостью.

При больших толщинах образца увеличивается вероятность попадания в проводящие цепочки горл меньших радиусов, за счет чего вытеснение жидкости будет происходить при больших центробежных ускорениях. В силу этого дифференциальные кривые распределения радиусов горл будут смещаться в сторону меньших значений радиусов.

С уменьшением толщины образца вытеснение жидкости становится возможным при меньших центробежных ускорениях, то есть через горла больших радиусов. Следовательно, путем изменения толщины можно смещать процесс вытеснения жидкости по всему реальному диапазону горл исследуемого образца, определяя при разных толщинах образца значения радиусов горл, относящихся к разным участкам этого диапазона.

Для определения исходной (наибольшей) толщины образца d₁ предлагается следующий способ. Исходная толщина d₁ определяется экспериментально по наличию в образце после центрифугирования на максимальном центробежном ускорении остаточного объема невытесненной жидкости V_ост. Это будет означать, что перколяционная вероятность для всех потенциально проницаемых радиусов горл не достигла значения равного 1. Ее максимальное значение можно найти как (V₀-V_ост)/ V₀, то есть как отношение вытесненного объема жидкости к общему V₀.

Уменьшение толщины образца следующего цикла измерений до значения d₂=d₁(V₀-V_ост)/V₀ будет соответствовать увеличению перколяционной вероятности до 1, то есть приведет к полному вытеснению жидкости в том же диапазоне центробежных ускорений. При этом процесс вытеснения жидкости сместится в область больших радиусов горл.

Взяв в качестве третьего значения толщины образца d₃=d₂/2, можно сместить процесс выделение жидкости в сторону еще больших значений радиусов горл.

В результате предлагаемого способа трехкратного снятия порограмм одного и того же образца максимумы дифференциальных кривых распределения радиусов горл, полученных из трех экспериментальных порограмм, оказываются смещенными, и их положения будут определять реальный диапазон радиусов горл, связывающих внутренние полости объекта.

Совпадение (или близость) положения максимумов дифференциальных кривых распределения пор по радиусам, полученных для разных толщин, будет свидетельствовать о монопористости объекта, то есть наличии в нем пор одного или близких радиусов.

В качестве примера реализации предлагаемого способа приводятся результаты измерения распределения радиусов пор в образце компактного вещества костной ткани, имеющей пористую структуру, соответствующую обеим моделям пористости. Пористое пространство компактной кости (внешнего слоя всех трубчатых костей) содержит систему продольных центральных каналов остеонов и систему лакун костных клеток, соединенных канальцами, радиусы которых (0,1-1 мкм) на порядок меньше радиусов лакун и центральных каналов (5-50 мкм). Поэтому вытеснение жидкости из образцов кости происходит вначале из центральных каналов, а затем из костных лакун, освобождение которых определяется радиусами канальцев, причем эти два этапа достаточно достоверно отражаются на порограмме. Методика проведения измерений подробно изложена в вышеуказанном прототипе изобретения и включает следующие основные моменты.

Экспериментальная порограмма есть кривая зависимости удельного объема пор (см³/г) от их радиусов. Общий объем пор и объем еще заполненных пор после центрифугирования на каждом из 9 фиксированных значений центробежного ускорения определялся взвешиванием образца и расчетом по формуле

V = M − m 0 m 0 ρ ( с м   3 г )

где m₀ - исходная масса образца, М - масса образца с находящейся в нем жидкостью, ρ - плотность используемой рабочей жидкости.

Минимальный радиус освободившихся пор определялся по формуле (1). Так как достижимые значения радиусов потенциально проницаемых пор меняются в эксперименте на три порядка (от 100 до 0,1 мкм), изменение объема заполненных пор строится от lg r (нм).

Поскольку определение распределения радиусов пор связано с графическим дифференцированием экспериментальной порограммы, она интерполировалась методом кубических сплайнов, при котором кривая интерполяции обязательно проходит через все экспериментальные точки [Алексеев Е.Р., Чеснокова О.В., Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9, М., NT Press, 2006, 492 с.].

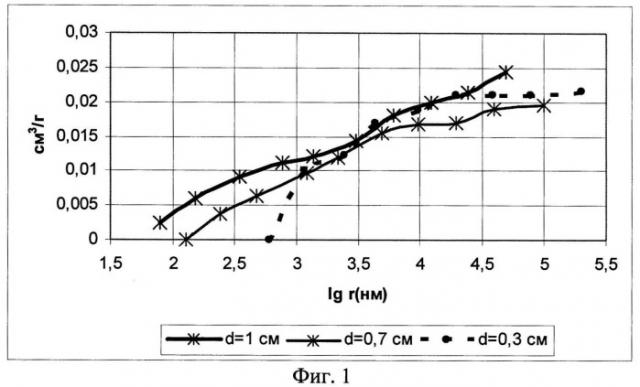
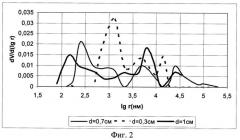
На Фиг.1 приведены порограммы, а на Фиг.2 - дифференциальные кривые распределения радиусов пор, полученные для трех толщин одного и того же образца: 1.0 см, 0.7 см, 0.3 см.

Из интегральных порограмм Фиг.1 видно, что с уменьшением толщины образца полное вытеснение жидкости происходит при больших радиусах канальцев (меньших значения центробежного ускорения), а для толщины 1 см остается не вытесненным остаточный объем пор V_ост=0,0025 см³/г при общем объеме лакун-канальцев порядка V₀=0,0116 см³/г. При этом перколяционная вероятность как отношение освободившегося объема пор к общему (V₀-V_ост)/ V₀=0,78, то есть меньше 1. Именно поэтому это значение толщины взято в качестве начального d₁.

При уменьшении толщины образца до 0,78 см можно ожидать, что для тех же потенциально проницаемых пор перколяционная вероятность возрастет в 1/0,78 раз, то есть достоверно примет максимальное значение, равное 1. Это и наблюдается для толщины образца d₂=0,7 см, при которой полное освобождение пор происходит при меньших значениях центробежного ускорения (через канальцы радиусами более 0,18 мкм). Еще большие значения радиусов потенциально проницаемых пор, в пределах которых произошло полное вытеснение жидкости, наблюдаются при толщине образца d₃=0,3 см, которая примерно вдвое меньше d2.

Основные результаты, вытекающие из кривых Фиг.2, полученных численным дифференцированием соответствующих кривых Фиг.1, сведены в таблицу 1, где lg r(нм) переведены в значения r (мкм). В таблице приведены положения максимумов и их ширина на уровне половины от максимального значения ординаты. I max и II max соответствуют радиусам центральных каналов и их значения мало меняются с изменением толщины образца, что свидетельствует о том, что система центральных каналов в данном случае хорошо соответствует модели параллельных непересекающихся цилиндров разных радиусов.

Таблица 1
Толщины образца d (см)	радиусы пор (мкм)
I max	II max	III max
1	35-25-16	9-6-4,4	0,5-0,2-0,1
0,7	39-25-20	10-5-3,2	0,5-0,3-0,2
0,3	20-14-10	10-5-3,2	2,2-1,2-0,5

Иная ситуация наблюдается для III max, характеризующего радиусы канальцев, поскольку его положение существенно меняется при изменении толщины образца. Система лакун и канальцев имеет пористую структуру типа «полостей и горл», для которой эта зависимость объяснялась выше. Но исследуется фактически один и тот же объект, причем определяются его удельные характеристики пористости (см/г), которые не зависят от его размеров. Очевидно, что экспериментально определяемое распределение пор исследуемого объекта будет существенно ближе к реальному, если спектр пор оценивать не по одному измерению с одной толщиной образца, а по всем трем. Тогда, как следует из значений III max таблицы 1, радиусы канальцев исследованного образца лежат в диапазоне 0,1-2,2 мкм, а преобладающие их значения - в диапазоне 0,2-1,2 мкм, что хорошо согласуется с известными данными, полученными с помощью электронной микроскопии [Травматология и ортопедия (руководство для врачей)//Под ред. чл.-корр. РАМН Ю.Г.Шапошникова. М.: Медицина, 1997, т.I, гл. 20 «Регенерация костной ткани»].

Способ центробежной порометрии, включающий пропитку образца смачивающей жидкостью с последующим удалением ее на фиксированных последовательно возрастающих центробежных ускорениях с определением количества жидкости в образце путем взвешивания, отличающийся тем, что проводят трехкратное снятие порограмм одного и того же образца при разных его толщинах, причем для первой порограммы используют толщину образца d₁, при которой после центрифугирования на максимальном центробежном ускорении остается объем не вытесненной жидкости V_ост, вторую порограмму снимают после уменьшения толщины образца до d₂=d₁(V₀-V_ост)/V₀, третью порограмму снимают для толщины того же образца d₃=d₂/2, а спектр радиусов пор исследуемого объекта определяют по положениям максимумов дифференциальных кривых распределения радиусов пор всех трех порограмм,где d₁ - толщина образца при снятии первой порограммы,d₂ - толщина образца при снятии второй порограммы,d₃ - толщина образца при снятии третьей порограммы,V₀ - общий объем пор,V_ост - остаточный объем не вытесненной из пор жидкости.