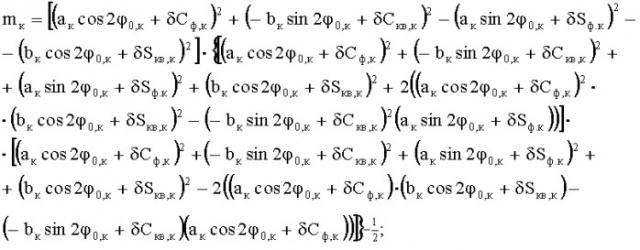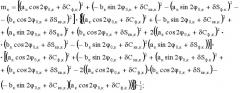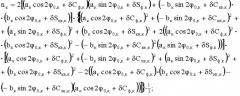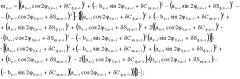Способ определения угла ориентации стоячей волны в твердотельном волновом гироскопе

Способ определения угла ориентации стоячей волны в твердотельном волновом гироскопе

Иллюстрации

Показать все

Реферат

Изобретение относится к области приборостроения и может быть использовано при производстве твердотельных волновых гироскопов и систем ориентации и навигации на их основе.

В современном гироскопическом приборостроении известны способы определения стоячей волны относительно резонатора твердотельного волнового гироскопа, в котором измеряют сигналы ω₁=Acosωtcos2υ,

ω₂=Acosωtsin2υ с датчиков угла гироскопа,

где А - амплитуда колебаний резонатора,

υ - угол ориентации стоячей волны,

ω - круговая частота колебаний рабочей формы, t - время. Используя эти сигналы ,угол ориентации волны определяют из выражения 2υ=arctgω₂/ω₁ (см., например, книгу В.А.Матвеева, В.И.Липатникова, А.В.Алехина «Проектирование волнового твердотельного гироскопа». - М., 1998, стр.50).

В этом способе погрешности определения сигналов ω₁ и ω₂ обуславливают гармонические ошибки определения угла ориентации волны в зависимости от самого угла υ. Для компенсации этих погрешностей требуются трудоемкие калибровочные операции. При этом также необходимо применение алгоритмов определения четверти, в которой находится волна, обеспечивающих требуемую точность нахождения υ, когда ω₁ стремится к нулю.

За прототип взят способ определения ориентации стоячей волны в твердотельном волновом гироскопе, использующий приращение на к-том такте вычислений угла ориентации волны к вычисленному углу на предыдущем к-1 такте (см. отчет ИПМ РАН №1274 «Теоретические исследования, разработка методик, программно-методического обеспечения, регулировки и испытаний твердотельного волнового гироскопа». - М., 1998).

В этом способе для определения ориентации стоячей волны в твердотельном волновом гироскопе по «измерительным» каналам косинуса «С» и синуса «S» измеряют сигналы датчиков углов гироскопа, выделяют синфазные С_ф, S_ф и квадратурные С_кв, S_кв составляющие этих сигналов. Определяют тригонометрические функции синуса и косинуса угла ориентации стоячей волны, используя синфазные и квадратурные составляющие сигналов датчиков углов

cos 4 ϕ 0 = ( C ф 2 + С к в 2 + S ф 2 + S к в 2 ) ⋅ ( A ⋅ B ) − 1 ;

sin 4 ϕ 0 = 2 ( C ф S ф + C к в S к в ) ⋅ ( A ⋅ B ) − 1 ,                                 (1)

где

A = C ф 2 + C к в 2 + S ф 2 + S к в 2 + 2 ⋅ ( C ф S к в − С к в S ф ) ;

B = C ф 2 + C к в 2 + S ф 2 + S к в 2 + 2 ⋅ ( C ф S к в − С к в S ф ) .

Для расчета угла 4φ₀ запоминают его значение и значения его тригонометрических функций на предыдущем шаге съема показаний к-1 4φ_0,к-1, соз4φ_0,к-1, sin4φ_0,к-1.

Вычисляют новые значения тригонометрических функций на к-м шаге cos4φ₀, sin4φ_0,к.

Новое значение угла 4φ_0,к рассчитывают по формуле

4 ϕ 0, к = 4 ϕ 0, к − 1 + Δ ( 4 ϕ 0 ) к ,                            (2)

где Δ(4φ₀)_к=sinΔ(4φ₀)_к=sin4φ_0,кcos4φ_0,к-1-cos4φ_0,кsin4φ_0,к-1.

Полученное значение угла вместе с его тригонометрическими функциями запоминают для использования на следующем шаге в качестве предыдущих.

Однако в существующем способе определения ориентации стоячей волны в твердотельном волновом гироскопе существует погрешность определения угла ориентации волны относительно резонатора при ошибках выработки синфазных и квадратурных составляющих сигналов датчиков угла гироскопа. Эти погрешности имеют зависимость от самого угла расположения волны гармонического характера.

В твердотельном волновом гироскопе вырабатываются приборные значения синфазных и квадратурных составляющих сигналов датчиков угла:

С ф п , к = С ф , к + δ С ф , к ; С ф п , к − 1 = С ф , к − 1 + δ С ф , к − 1 ; С к в п , к = С к в , к + δ С к в , к ; С к в п , к − 1 = С к в , к − 1 + δ С к в , к − 1 ; S ф п , к = S ф , к + δ S ф , к ; S ф п , к − 1 = S ф , к − 1 + δ S ф , к − 1 ; S к в п , к = S к в , к + δ S к в , к ; S к в п , к − 1 = S к в , к − 1 + δ S к в , к − 1             (3)

где

С_ф,к, S_ф,к, С_ф,к-1, S_ф,к-1 - истинные значения синфазных составляющих по каналам косинуса «С» и синуса «S» на к и к-1 тактах вычислений;

С_кв,к, S_кв,к, С_кв,к-1, S_кв,к-1 - истинные значения квадратурных составляющих по каналам «С» и «S» на к и к-1 тактах;

δС_ф,к, δS_ф,к, δС_ф,к-1, δS_ф,к-1 - погрешности выработки синфазных составляющих по каналам «С» и «S» на к и к-1 тактах;

δС_кв,к, δS_кв,к, δ_Скв,к-1, δS_кв,к-1 - погрешности выработки квадратурных составляющих по каналам «С» и «S» на к и к-1 тактах.

Вырабатываемые приборные значения углов на к-м и к-1 такте и приращение угла на к-м такте:

4 ϕ 0 п , к = 4 ϕ 0, к + δ 4 ϕ 0, к ; 4 ϕ 0 п , к = 4 ϕ 0, к + δ 4 ϕ 0, к ;                                     (4) Δ ( 4 ϕ 0 п ) к = Δ ( 4 ϕ 0 ) к + δ Δ ( 4 ϕ 0 ) к ,

где

4φ_0,к,4φ_0,к-1 - истинные значения углов на к и к-1 тактах;

Δ(4φ₀)_к - истинное значение приращения угла на к такте;

δ4φ_0,к; Δ4φ_0,к-1 - погрешности выработки углов на к и к-1 тактах;

δΔ(4φ₀)_к - погрешность выработки угла на к-м такте.

С учетом (4) погрешность определения угла ориентации волны на к-м такте можно представить

δ 4 ϕ 0, к = δ 4 ϕ 0, к − 1 + δ Δ ( 4 ϕ 0 ) к .                                (5)

Рассмотрим погрешность определения угла, вызванную погрешностью приращения угла δΔ(4φ₀)_к.

При точном задании начального угла эта погрешность обуславливает погрешность определения угла ориентации волны.

В выражениях (3) истинные значения синфазных и квадратурных составляющих по измерительным каналам косинуса и синуса можно представить:

С ф , к = a cos 2 ϕ 0. к , С ф , к − 1 = a cos 2 ϕ 0. к − 1 , С к в , к = b sin 2 ϕ 0, к , С к в , к − 1 = b sin 2 ϕ 0, к − 1 , S ф , к = a cos 2 ϕ 0. к , S ф , к − 1 = a cos 2 ϕ 0. к − 1 , S к в , к = b sin 2 ϕ 0, к , S к в , к − 1 = b sin 2 ϕ 0, к − 1 ,             (6)

где

a - большая полуось эллипсовидной траектории точки в плоскости CS, изображающей состояние резонатора, b - малая полуось эллипсовидной траектории точки в плоскости CS, изображающей состояние резонатора.

Используя выражения (1), (2), (3), (6), погрешность приращения угла можно представить в виде:

δ Δ ( 4 ϕ 0 ) к = n к m к − 1 − m к n к − 1 − Δ ( 4 ϕ 0 ) к ,                                  (7)

где

m к = [ ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 + ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 − ( а к sin 2 ϕ 0, к + δ S ф . к ) 2 − − ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 ] ⋅ { [ ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 + ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 + + ( а к sin 2 ϕ 0, к + δ S ф . к ) 2 + ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 + 2 ( ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 ⋅ ⋅ ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 − ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 ( а к sin 2 ϕ 0, к + δ S ф . к ) ) ] ⋅ ⋅ [ ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 + ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 + ( а к sin 2 ϕ 0, к + δ S ф . к ) 2 + + ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 − 2 ( ( а к cos 2 ϕ 0, к + δ С ф , к ) ⋅ ( b к cos 2 ϕ 0, к + δ S к в , к ) − ( − b к sin 2 ϕ 0, к + δ С к в , к ) ( а к cos 2 ϕ 0, к + δ С ф , к ) ) ] } − 1 2 ;

n к = 2 [ ( а к cos 2 ϕ 0, к + δ С ф , к ) ( а к sin 2 ϕ 0, к + δ S ф . к ) + ( − b к sin 2 ϕ 0, к + δ С к в , к ) ⋅ ⋅ ( b к cos 2 ϕ 0, к + δ S к в , к ) ] ⋅ { [ ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 + ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 + + ( а к sin 2 ϕ 0, к + δ S ф . к ) 2 + ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 + 2 ( ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 ⋅ ⋅ ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 − ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 ( а к sin 2 ϕ 0, к + δ S ф . к ) ) ] ⋅ ⋅ [ ( а к cos 2 ϕ 0, к + δ С ф , к ) 2 + ( − b к sin 2 ϕ 0, к + δ С к в , к ) 2 + ( а к sin 2 ϕ 0, к + δ S ф . к ) 2 + + ( b к cos 2 ϕ 0, к + δ S к в , к ) 2 − 2 ( ( а к cos 2 ϕ 0, к + δ С ф , к ) ⋅ ( b к cos 2 ϕ 0, к + δ S к в , к ) − ( − b к sin 2 ϕ 0, к + δ С к в , к ) ( а к cos 2 ϕ 0, к + δ С ф , к ) ) ] } − 1 2 ;

m к − 1 = [ ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 + ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 − ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) 2 − − ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 ] ⋅ { [ ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 + ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 + + ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) 2 + ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 + 2 ( ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 ⋅ ⋅ ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 − ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) ) ] ⋅ ⋅ [ ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 + ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 + ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) 2 + + ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 − 2 ( ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) ⋅ ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) − ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) ) ] } − 1 2 ;

n к − 1 = 2 [ ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) + ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) ⋅ ⋅ ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) ] ⋅ { [ ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 + ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 + + ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) 2 + ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 + 2 ( ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 ⋅ ⋅ ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 − ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) ) ] ⋅ ⋅ [ ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) 2 + ( − b к − 1 sin 2 ϕ 0, к − 1 + δ С к в , к − 1 ) 2 + ( а к − 1 sin 2 ϕ 0, к − 1 + δ S ф . к − 1 ) 2 + + ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) 2 − 2 ( ( а к − 1 cos 2 ϕ 0, к − 1 + δ С ф , к − 1 ) ⋅ ( b к − 1 cos 2 ϕ 0, к − 1 + δ S к в , к − 1 ) − ( − b к sin 2 ϕ 0, к + δ С к в , к ) ( а к cos 2 ϕ 0, к + δ С ф , к ) ) ] } − 1 2 ;

Δ(4φ₀)_к=sin4φ_0,кcos4φ_0,к-1-cos4φ_0,кsin4φ_0,к-1.

Компьютерное моделирование с использованием выражения (7) показало, что погрешности выработки синфазных и квадратурных составляющих вызывают ошибки в определении приращений угла ориентации волны. Эти ошибки возникают при наличии прецессионного движения волны вследствие входной угловой скорости или собственной скорости дрейфа.

На фиг.1 показаны погрешности определения приращения угла ориентации волны на такте при ошибках выработки синфазных и квадратурных составляющих по каналам косинуса и синуса датчика угла на разных углах ориентации волны и разных скоростях ее прецессии:

1 - скорость прецессии волны 12,4°/ч;

2 - скорость прецессии волны 24,8°/ч;

3 - скорость прецессии волны 37,2°/ч.

Погрешность приращения угла ориентации волны имеет синусоидальный характер с периодичностью 180° угла ориентации волны φ₀, ее фазовый сдвиг и наличие постоянной составляющей зависят от величин и соотношений ошибок выработки синфазных и квадратурных составляющих.

Ширина трубки изменения этой погрешности на угле периодичности также обусловлена величиной скорости прецессии волны.

При обработке информации с гироскопа известным способом эти ошибки выработки приращения угла ориентации стоячей волны накапливаются, что снижает точностные характеристики приборов ориентации и навигации.

Техническим результатом, который может быть получен при осуществлении настоящего изобретения, является повышение точности выработки угла ориентации стоячей волны твердотельного волнового гироскопа относительно его резонатора.

Технический результат достигается тем, что в известном способе определения угла ориентации стоячей волны в твердотельном волновом гироскопе, включающем измерение сигналов с синусного и косинусного каналов датчика угла гироскопа, выделение синфазных и квадратурных составляющих этих сигналов, определение тригонометрических функций синуса и косинуса угла ориентации стоячей волны, используя синфазные и квадратурные составляющие сигналов, вычисление угла ориентации волны относительно резонатора гироскопа на каждом такте вычислений по формуле с применением тригонометрических функций синуса и косинуса угла волны, полученных для к-1-го и к-го тактов, а также значение угла ориентации волны на к-1-м такте, дополнительно предварительно располагают гироскоп на платформе поворотного стола таким образом, чтобы его входная ось совпадала по направлению с осью вращения платформы и была направлена вертикально, задают платформе первое эталонное значение угловой скорости и в угловом диапазоне ориентации стоячей волны относительно резонатора ±90° измеряют показания гироскопа, задают второе эталонное значение угловой скорости платформы и на этом же угловом диапазоне ориентации волны измеряют показания гироскопа, определяют разницу в ширине трубок изменений показаний гироскопа в заданном угловом диапазоне ее ориентации при разных угловых скоростях платформы, подбирают корректирующие коэффициенты для вырабатываемых приборных значений синфазных и квадратурных составляющих синусного и косинусного каналов датчика угла гироскопа, минимизирующих эту разницу в ширине трубок изменений показаний гироскопа, после чего в рабочем режиме, используя подобранные корректирующие коэффициенты, определяют угол ориентации стоячей волны относительно резонатора по формуле

ϕ 0, к = 0,25 ( n к m к − 1 − m к n к − 1 ) + ϕ 0, к − 1 ,                                    (8)

где

m к = [ ( С ф п , к − Δ С ф ) 2 + ( С к в п , к − Δ С к в ) 2 − ( S ф п , к − Δ S ф ) 2 − ( S к в п , к − Δ S к в ) 2 ] ⋅ ⋅ { [ ( С ф п , к − Δ С ф ) 2 + ( С к в п , к − Δ С к в ) 2 + ( S ф п , к − Δ S ф ) 2 + ( S к в п , к − Δ S к в ) 2 + + 2 ( ( С ф п , к − Δ С ф ) ( S к в п , к − Δ S к в ) − ( С к в , к − Δ С к в ) ( S ф п , к − Δ S ф ) ) ] ⋅ ⋅ [