Способ измерения сдвига фаз

Способ измерения сдвига фаз

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике, а именно измерительной технике, и имеет целью повысить точность измерения фазового сдвига двух квазигармонических сигналов с медленными по сравнению с несущей частотой изменениями огибающей и частоты при наличии аддитивных и мультипликативных помех.

Известен способ определения сдвига фаз двух синусоидальных сигналов [1], как арктангенса отношения двух величин, которые формируют из измеренных мгновенных значений сигналов. Недостатком способа является ограничение области его применимости синусоидальными сигналами с постоянными амплитудами и частотами, наличие амплитудной и частотной модуляции уменьшает точность измерения сдвига фаз.

Наиболее близким к заявляемому способу по максимальному количеству сходных признаков является способ широкополосной цифровой фазометрии, который принят за прототип [2], заключающийся в том, что посредством двух аналого-цифровых преобразователей и двух распределителей отсчетов сигналов на четные и нечетные из первого и второго сигналов формируют третий и четвертый сигналы путем задержки первого и второго сигналов на один интервал, все произведения четных и нечетных сигналов, первую величину как разность произведения второго сигнала на третий и первого сигнала на четвертый, вторую величину как сумму произведения первого сигнала на второй и третьего сигнала на четвертый и оценку фазового сдвига между первым и вторым сигналами как арктангенс отношения усредненных по времени значений первой и второй величин.

Недостатком этого способа является высокая погрешность измерения сдвига фаз между квазигармоническими сигналами с меняющимися огибающими и мгновенными частотами. Действительно, пусть первый и второй квазигармонические сигналы, между которыми измеряется сдвиг фаз, имеют вид

x₁(t)=a ₁(t)sin[θ(t)+φ₁], x₂(t)=a ₂(t)sin[θ(t)+φ₂],

где a ₁(t), a ₂(t), φ₁ и φ₂ - огибающие и начальные фазы первого и второго сигналов, соответственно, причем выполняются условия медленного изменения огибающих и мгновенной частоты

| ω ˙ ( t ) | < < ω 2 ( t ) ,   | a ˙ 1 ( t ) | < < a 1 ( t ) ω ( t ) ,   | a ˙ 2 ( t ) | < < a 2 ( t ) ω ( t ) ,  

где ω ( t ) = θ ˙ ( t ) - мгновенная частота. Тогда третий и четвертый сигналы будут иметь вид

x 3 ( t ) = x 1 ( t − Δ ) ≈ [ a 1 ( t ) − a ˙ 1 ( t ) Δ ] sin [ θ ( t ) − ω ( t ) Δ + ϕ 1 ] ,

x 4 ( t ) = x 2 ( t − Δ ) ≈ [ a 2 ( t ) − a ˙ 2 ( t ) Δ ] sin [ θ ( t ) − ω ( t ) Δ + ϕ 2 ] ,

где Δ - интервал задержки.

Первая и вторая величины имеют вид

A₁(t)=x₃(t)x₂(t)-x₁(t)x₄(t)≈a ₁(t)a ₂(t)sin(φ(t)Δ)sin(φ)+ΔA₁(t)

A₂(t)=x₁(t)x₂(t)+x₃(t)x₄(t)≈

≈a ₁(t)a ₂(t)[cos(φ)-cos(ω(t)Δ)cos(2θ(t)-ω(t)Δ+φ₁+φ₂)]+ΔA₂(t),

Δ A 1 ( t ) = Δ 2 [ a 1 ( t ) a ˙ 2 ( t ) cos ( ω Δ + ϕ ) − a 2 ( t ) a ˙ 1 ( t ) cos ( ω Δ − ϕ ) ] +

+ Δ 2 [ a 2 ( t ) a ˙ 1 ( t ) − a 1 ( t ) a 2 ( t ) ] cos ( 2 θ ( t ) − ω Δ + ϕ 1 + ϕ 2 ) .

Δ A 2 ( t ) = − Δ [ a 1 ( t ) a 2 ( t ) + a 1 ( t ) a ˙ 2 ( t ) ] [ cos ( ϕ ) − cos ( 2 θ ( t ) − 2 ω ( t ) Δ + ϕ 1 + ϕ 2 ) ] ,

где φ=φ₁-φ₂ - измеряемый сдвиг фаз.

Разлагая числитель и знаменатель отношения усредненных по отрезку времени T>>1/ω(t) первой и второй величин в ряд вблизи ωΔ=π/2, получим:

〈 A 1 ( t ) 〉 〈 A 2 ( t ) 〉 = sin ( ϕ ) sin ( ω ( t ) Δ ) + 〈 Δ A 1 ( t ) 〉 a 1 ( t ) a 2 ( t ) cos ( ϕ ) + 〈 Δ A 2 ( t ) 〉 a 1 ( t ) a 2 ( t ) ≈

≈ t g ( ϕ ) { 1 − 1 2 ( π 2 − ω ( t ) Δ ) 2 + α ( t ) Δ d ( a 1 a 2 ) / d t a 1 a 2 } ,

где α(t) - величина порядка единицы. Таким образом, погрешность оценки сдвига фаз напрямую зависит от близости величины ω(t)Δ к величине π/2 и от скорости изменения огибающих. Для амплитудно-модулированных квазигармонических сигналов с медленно меняющейся в широких пределах мгновенной частотой и эта погрешность может быть довольно велика.

Целью изобретения является уменьшение погрешности измерения сдвига фаз квазигармонических сигналов с медленно меняющимися амплитудами и частотой при наличии аддитивной и мультипликативной помех.

Технический результат достигается тем, что в способе измерения сдвига фаз формируют третий и четвертый сигналы путем задержки первого и второго сигналов на один интервал, все произведения четных и нечетных сигналов, из которых формируют первую и вторую величины, оценку измеряемого сдвига фаз между первым и вторым сигналами как арктангенс отношения усредненных по времени значений первой и второй величин. При этом дополнительно формируют пятый, седьмой и девятый сигналы путем задержки первого сигнала на два, три и четыре интервала, соответственно, шестой, восьмой и десятый сигналы путем задержки второго сигнала на два, три и четыре интервала, соответственно, формируют третью величину как разность произведения второго сигнала на девятый сигнал и произведения первого сигнала на десятый сигнал, четвертую величину как разность произведения четвертого сигнала на седьмой сигнал и произведения третьего сигнала на восьмой сигнал, пятую величину формируют как разность произведения четвертого сигнала на седьмой сигнал и произведения пятого сигнала на шестой сигнал, шестую величину как разность произведения третьего сигнала на восьмой сигнал и произведения пятого сигнала на шестой сигнал, седьмую величину как сумму произведения четвертого сигнала на седьмой сигнал и произведения третьего сигнала на восьмой сигнал, восьмую величину как сумму произведения третьего сигнала на четвертый сигнал и произведения седьмого сигнала на восьмой сигнал, причем измерение проводится в два этапа, на первом этапе первую величину формируют как произведение четвертой величины на сумму пятой и шестой величин и на квадратный корень разности квадрата удвоенной четвертой величины и квадрата третьей величины, а вторую величину формируют как произведение квадрата суммы пятой и шестой величин на сумму удвоенной четвертой и третьей величин, на втором этапе первую величину формируют как произведение модуля четвертой величины на разность произведений третьей и седьмой величин и удвоенной четвертой и восьмой величин и на квадратный корень разности квадрата удвоенной четвертой величины и квадрата третьей величины, а вторую величину формируют как квадрат разности произведения третьей и седьмой величин и произведения удвоенной четвертой и восьмой величин, и из полученных на первом и втором этапах оценок сдвига фаз выбирается оценка, имеющая минимальное среднеквадратичное отклонение.

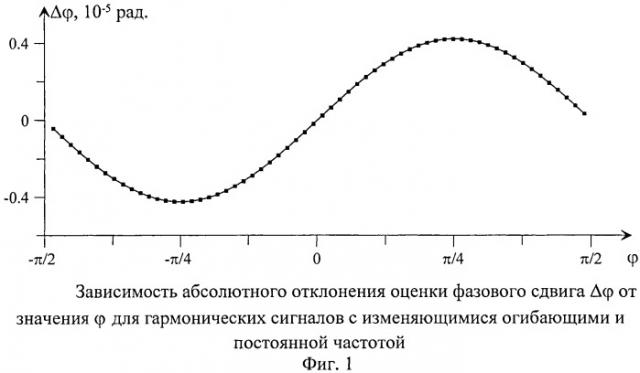
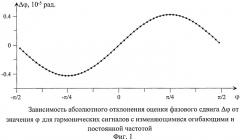
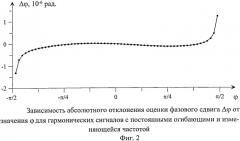
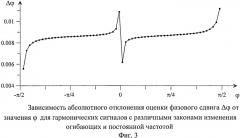
На чертежах представлено: на фиг.1 изображена зависимость абсолютного отклонения оценки фазового сдвига Δφ от значения φ для гармонических сигналов с изменяющимися огибающими и постоянной частотой; на фиг.2 - зависимость абсолютного отклонения оценки фазового сдвига Δφ от значения φ для гармонических сигналов с постоянными огибающими и изменяющейся частотой; на фиг.3 - зависимость абсолютного отклонения оценки фазового сдвига Δφ от значения φ для гармонических сигналов с различными законами изменения огибающих и постоянной частотой; на фиг.4 - систематическая погрешность оценки разности фаз гармонических сигналов в зависимости от значения φ при СКО шума σ_ξ=0,01; на фиг.5 - случайная погрешность оценки разности фаз гармонических сигналов в зависимости от значения φ при СКО шума σ_ξ=0,01.

Способ осуществляют следующим образом. Формируемые третья, четвертая, пятая, шестая, седьмая и восьмая величины, соответственно, имеют вид

A₃(t)=x₁(t-4Δ)x₂(t)-x₁(t)x₂(t-4Δ),

A₄(t)=x₁(t-3Δ)x₂(t-Δ)-x₁(t-Δ)x₂(t-3Δ),

A₅(t)=x₁(t-3Δ)x₂(t-Δ)-x₁(t-2Δ)x₂(t-2Δ),

A₆(t)=x₁(t-Δ)x₂(t-3Δ)-x₁(t-2Δ)x₂(t-2Δ),

A₇(t)=x₁(t-3Δ)x₂(t-Δ)+x₁(t-Δ)x₂(t-3Δ).

Тогда на первом этапе измерения первая и вторая величины имеют вид

A 1 ( t ) = A 4 ( t ) ( A 5 ( t ) + A 6 ( t ) ) 4 A 4 2 ( t ) − A 3 2 ( t ) ,

A₂(t)=(A₅(t)+A₆(t)²(2A₄(t)+A₃(t)),

и полученная на первом этапе оценка φ₁ сдвига фаз между первым и вторым сигналами на отрезке длительностью N интервалов Δ имеет вид

ϕ 1 ≈ a r c t g [ ∑ n = 4 N − 1 A 4 [ n ] ( A 5 [ n ] + A 6 [ n ] ) 4 A 4 2 [ n ] − A 3 2 [ n ] ∑ n = 4 N − 1 ( A 5 [ n ] + A 6 [ n ] ) 2 ( 2 A 4 [ n ] + A 3 [ n ] ) ] ,

где обозначено A_i[n]=A_i(nΔ), i=1, 2, 3, 4, 5, 6, 7, 8. На втором этапе измерения первая и вторая величины имеют вид

A 1 ( t ) = | A 4 [ n ] | ( A 3 [ n ] A 7 [ n ] − 2 A 4 [ n ] A 8 [ n ] ) 4 A 4 2 [ n ] − A 3 2 [ n ] ,

A₂(t)=(A₃[n]A₇[n]-2A₄[n]A₈[n])²

и полученная на втором этапе оценка φ₂ сдвига фаз между первым и вторым сигналами на отрезке длительностью N интервалов Δ имеет вид ϕ 2 ≈ a r c t g [ ∑ n = 4 N − 1 | A 4 [ n ] | ( A 3 [ n ] A 7 [ n ] − 2 A 4 [ n ] A 8 [ n ] ) 4 A 4 2 [ n ] − A 3 2 [ n ] ∑ n = 4 N − 1 ( A 3 [ n ] A 7 [ n ] − 2 A 4 [ n ] A 8 [ n ] ) 2 ] .

При наличии аддитивного и мультипликативного шумов обе полученные оценки могут испытывать флуктуации за время измерения, поэтому в качестве оценки измеряемого сдвига фаз φ между первым и вторым сигналами из оценок φ₂ и φ₂ выбирается оценка с меньшим среднеквадратичным отклонением.

Численное моделирование полученных выражений подтверждает промышленную применимость предложенного способа. Погрешность определения сдвига фаз Δφ чисто гармонических сигналов при отсутствии шума не превышает 10^-14 рад; здесь и далее N=1333, Δ=1. При наличии амплитудной или частотной модуляции, а также аддитивного шума погрешность возрастает. На фиг.1 представлено отклонение фазового сдвига Δφ, полученное для сигналов с одинаковыми законами изменения огибающих и фиксированной частотой f₀=0,147:

x₁[n]=(1+0,17sin(2π·0,0012·n))sin(2π·0,147·n+φ),

x2[n]=(1+0,17sin(2π·0,0012·n))sin(2π·0,147·n).

Огибающая сигналов изменяется от минимума до максимума примерно на 35%, а абсолютное отклонение фазового сдвига остается на уровне 10^-6. Аналогичные результаты получаются для сигналов с постоянными огибающими и изменяющейся частотой (фиг.2):

x₁[n]=sin(2π·0,093·{1+0,15·cos(2π·0,00053·n)}·n+φ),

x₂[n]=sin(2π·0,093·{1+0,15·cos(2π·0,00053·n)}·n).

При несовпадающих законах изменения огибающих появляется сингулярность при малых значениях φ, а также смещение оценки, которое может быть как положительным, так и отрицательным. На фиг.3 показана абсолютная погрешность определения фазового сдвига для следующих моделей сигналов:

x₁[n]=(1+0,11·sin(2π·0,0019·n))sin(2π·0,013·n+φ),

x₂[n]=(1+0,0011·n)sin(2π·0,013·n).

Статистические свойства способа исследовались путем обработки смеси сигналов с аддитивным узкополосным шумом. На фиг.4 и 5 представлены систематическая <Δφ>и случайная σ_φ погрешности определения фазового сдвига от значения φ, полученные по 50 реализациям, для сигналов с постоянными единичными огибающими и фиксированной частотой f₀=0,107.

Численные эксперименты показывают, что оптимальное значение интервала Δ лежит в диапазоне от T/6 до T/4, где Т - среднее за время измерения значение периода сигнала. При соблюдении этого условия погрешность измерения сдвига фаз предложенным способом при наличии 15% амплитудной и частотной модуляции в 10⁵ раз меньше, чем у прототипа [2].

Источники информации

1. Келехсаев Б.Г. Способ определения сдвига фаз двух синусоидальных сигналов. Патент РФ №2039361, опубл. 09.07.1995.

2. Смирнов В.Н., Кучеров М.В. Широкополосный цифровой фазометр // Вопросы радиоэлектроники. 2004, №1. С. 33-41 (прототип).

Способ измерения сдвига фаз, заключающийся в том, что формируют третий и четвертый сигналы путем задержки первого и второго сигналов на один интервал, все произведения четных и нечетных сигналов, из которых формируют первую и вторую величины, оценку измеряемого сдвига фаз между первым и вторым сигналами как арктангенс отношения усредненных по времени значений первой и второй величин, отличающийся тем, что дополнительно формируют пятый, седьмой и девятый сигналы путем задержки первого сигнала на два, три и четыре интервала, соответственно, шестой, восьмой и десятый сигналы путем задержки второго сигнала на два, три и четыре интервала, соответственно, формируют третью величину как разность произведения второго сигнала на девятый сигнал и произведения первого сигнала на десятый сигнал, четвертую величину как разность произведения четвертого сигнала на седьмой сигнал и произведения третьего сигнала на восьмой сигнал, пятую величину формируют как разность произведения четвертого сигнала на седьмой сигнал и произведения пятого сигнала на шестой сигнал, шестую величину как разность произведения третьего сигнала на восьмой сигнал и произведения пятого сигнала на шестой сигнал, седьмую величину как сумму произведения четвертого сигнала на седьмой сигнал и произведения третьего сигнала на восьмой сигнал, восьмую величину как сумму произведения третьего сигнала на четвертый сигнал и произведения седьмого сигнала на восьмой сигнал, причем измерение проводится в два этапа, на первом этапе первую величину формируют как произведение четвертой величины на сумму пятой и шестой величин и на квадратный корень разности квадрата удвоенной четвертой величины и квадрата третьей величины, а вторую величину формируют как произведение квадрата суммы пятой и шестой величин на сумму удвоенной четвертой и третьей величин, на втором этапе первую величину формируют как произведение модуля четвертой величины на разность произведений третьей и седьмой величин и удвоенной четвертой и восьмой величин и на квадратный корень разности квадрата удвоенной четвертой величины и квадрата третьей величины, а вторую величину формируют как квадрат разности произведения третьей и седьмой величин и произведения удвоенной четвертой и восьмой величин, и из полученных на первом и втором этапах оценок сдвига фаз выбирается оценка, имеющая минимальное среднеквадратичное отклонение.