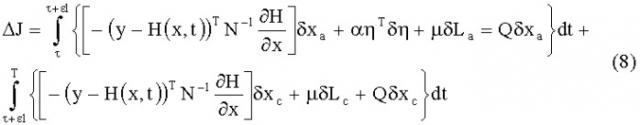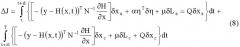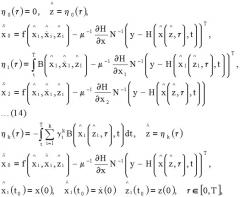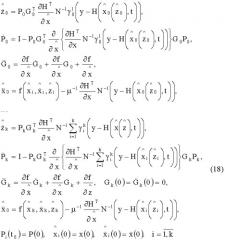Устройство идентификации лагранжевых динамических систем на основе итерационной регуляризации

Устройство идентификации лагранжевых динамических систем на основе итерационной регуляризации

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой вычислительной техники и может быть использовано в автоматических и автоматизированных системах различного назначения для идентификации параметров.

Известно устройство идентификации параметров динамических систем, в основе которого лежит фильтр Калмана. Его эффективное функционирование возможно в случае априорной определенности законов распределения внешних воздействий, что является существенным недостатком.

Наиболее близким по технической сущности к заявленному изобретению является устройство идентификации параметров динамических систем на основе вариационных принципов [1]. Однако его использование в условиях неизвестных воздействий не позволяет получить требуемую точность.

Цель изобретения - повысить точность идентификации параметров динамических систем. Указанный технический результат достигается за счет устройства идентификации Лагранжевых динамических систем на основе итерационной регуляризации, которое содержит следующие блоки: первый, второй блоки хранения констант; первый, второй, третий блоки формирования функций f ( x ^ i , x ˙ ^ i , z ^ i ) , H ( x ^ i , ( z ^ i ) , t ) , (1-γ_i-1), соответственно; первый, второй, третий, четвертый, пятый блоки формирования производной; первый, второй, третий, четвертый, пятый, шестой, седьмой, восьмой, девятый, десятый, одиннадцатый блоки формирования произведения; первый, второй, третий блоки формирования разности; первый, второй, третий блоки формирования суммы; первый, второй блоки транспонирования; первый, второй, третий, четвертый, пятый, шестой блоки интегрирования; при этом на первый информационный вход первого блока хранения констант, который является входом устройства, поступает значение наблюдаемой величины; первый информационный выход первого блока хранения констант соединен с первым информационным входом первого блока формирования произведения; второй, третий и четвертый информационные выходы первого блока хранения констант соединены соответственно с первым, вторым и третьим информационными входами первого блока формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) ; второй и четвертый информационные выходы первого блока хранения констант соединены соответственно с первым и вторым информационными входами второго блока формирования функции H ( x ^ i , ( z ^ i ) , t ) ; пятый информационный выход первого блока хранения констант соединен со вторыми информационными входами первого, второго, третьего и шестого блоков интегрирования, а также с первыми информационными входами четвертого и пятого блоков интегрирования; шестой информационный выход первого блока хранения констант соединен со вторым информационным входом второго блока формирования разности; седьмой информационный выход первого блока хранения констант соединен с первым информационным входом третьего блока формирования функции (1-γ_i-1); восьмой информационный выход первого блока хранения констант соединен со вторым информационным входом третьего блока формирования функции (1-γ_i-1) и третьим информационным входом первого блока формирования суммы; девятый информационный выход первого блока хранения констант соединен со вторым информационным входом третьего блока формирования произведения; десятый информационный выход первого блока хранения констант соединен с первым и вторым информационными входами соответственно шестого и девятого блоков формирования произведения; одиннадцатый информационный выход первого блока хранения констант соединен с первым информационным входом второго блока транспонирования, а также с первыми информационными входами восьмого и девятого блоков формирования произведения; двенадцатый информационный выход первого блока хранения констант соединен с первым информационным входом седьмого блока формирования произведения; тринадцатый информационный выход первого блока хранения констант соединен с первым информационным входом третьего блока формирования разности; информационный выход первого блока формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) соединен со вторым информационным

входом первого блока формирования разности, а также с первыми информационными входами второго, третьего и четвертого блоков формирования производной; информационный выход второго блока формирования функции H ( x ^ i , ( z ^ i ) , t ) соединен с первыми информационными входами первого блока транспонирования и второго блока формирования разности, информационный выход которого соединен с первым информационным входом второго блока формирования произведения, 1 информационный выход которого соединен с первыми информационными входами второго блока хранения констант и первого блока формирования суммы; информационный выход второго блока хранения констант соединен со вторым информационным входом первого блока формирования суммы, информационный выход которого соединен с первым информационным входом третьего блока формирования произведения, информационный выход которого соединен с первым информационным входом четвертого блока формирования произведения; информационный выход первого блока транспонирования соединен с первым информационным входом первого блока формирования производной, информационный выход которого соединен со вторым информационным входом четвертого блока формирования произведения, информационный выход которого соединен соответственно со вторым информационным входом первого блока формирования произведения и первыми информационными входами пятого блока формирования произведения и пятого блока формирования производной, информационный выход которого соединен с первым информационным входом десятого блока формирования произведения; информационный выход второго блока транспонирования соединен со вторым информационным входом шестого блока формирования произведения, информационный выход которого соединен соответственно со вторыми информационными входами пятого и десятого блоков формирования произведения, информационный выход которого соединен со вторым информационным входом одиннадцатого блока формирования произведения; информационный выход девятого блока формирования произведения соединен с первым информационным входом одиннадцатого блока формирования произведения, информационный выход которого соединен со вторым информационным входом третьего блока формирования разности, информационный выход которого соединен с первым информационным входом шестого блока интегрирования, информационный выход которого соединен с первым и вторым информационными входами соответственно шестого и девятого блоков формирования произведения; информационный выход первого блока формирования произведения соединен с первым информационным входом первого блока формирования разности, информационный выход которого соединен с первым информационным входом первого блока интегрирования, информационный выход которого соединен со вторым информационным входом первого блока формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) и первым информационным входом второго блока интегрирования, информационный выход которого соединен с первыми информационными входами первого и второго блоков формирования функции H ( x ^ i , ( z ^ i ) , t ) ; информационный выход пятого блока формирования произведения соединен с первым информационным входом третьего блока интегрирования, информационный выход которого является выходом устройства, с него же снимается значение искомого вектора идентификации параметров и подается на второй и третий информационные входы соответственно второго и первого блоков формирования функции H ( x ^ i , ( z ^ i ) , t ) , и f ( x ^ i , x ˙ ^ i , z ^ i ) ; информационный выход второго блока формирования производной соединен со вторым информационным входом седьмого блока формирования произведения, информационный выход которого соединен с первым информационным входом второго блока формирования суммы; информационный выход третьего блока формирования производной соединен со вторым информационным входом восьмого блока формирования произведения, информационный выход которого соединен со вторым информационным входом второго блока формирования суммы, информационный выход которого соединен с первым информационным входом третьего блока формирования суммы; информационный выход четвертого блока формирования производной соединен со вторым информационным входом третьего блока формирования суммы, информационный выход которого соединен со вторым информационным входом пятого блока интегрирования, информационный выход которого соединен с первым информационным входом седьмого блока формирования произведения и вторым информационным входом четвертого блока интегрирования, информационный выход которого соединен с первым информационным входом второго блока транспонирования, а также с первыми информационными входами восьмого и девятого блоков формирования умножения.

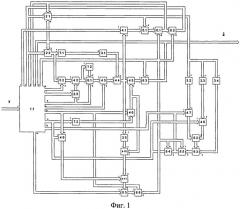
Сущность изобретения поясняется чертежами, где на фиг.1 представлено устройство идентификации параметров Лагранжевых динамических систем на основе итерационной регуляризации, которое содержит:

1.1 - первый блок хранения констант;

1.2 - второй блок хранения констант;

2.1- первый блок формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) ;

2.2 - второй блок формирования функции H ( x ^ i , ( z ^ i ) , t ) ;

2.3 - третий блок формирования функции (1-γ_i1);

3.1 - первый блок формирования производной;

3.2 - второй блок формирования производной;

3.3 - третий блок формирования производной;

3.4 - четвертый блок формирования производной;

3.5 - пятый блок формирования производной;

4.1 - первый блок формирования произведения;

4.2 - второй блок формирования произведения;

4.3 - третий блок формирования произведения;

4.4 - четвертый блок формирования произведения;

4.5 - пятый блок формирования произведения;

4.6 - шестой блок формирования произведения;

4.7 - седьмой блок формирования произведения;

4.8 - восьмой блок формирования произведения;

4.9 - девятый блок формирования произведения;

4.10 - десятый блок формирования произведения;

4.11 - одиннадцатый блок формирования произведения;

5.1 - первый блок формирования разности;

5.2 - второй блок формирования разности;

5.3 - третий блок формирования разности;

6.1 - первый блок формирования суммы;

6.2 - второй блок формирования суммы;

6.3 - третий блок формирования суммы;

7.1 - первый блок транспонирования;

7.2 - второй блок транспонирования;

8.1 - первый блок интегрирования;

8.2 - второй блок интегрирования;

8.3 - третий блок интегрирования;

8.4 - четвертый блок интегрирования;

8.5 - пятый блок интегрирования;

8.6 - шестой блок интегрирования.

На фиг.2 представлен первый блок интегрирования:

8.1.1 - блок формирования произведения;

8.1.2 - блок формирования суммы;

8.1.3 - линия задержки.

Устройство идентификации Лагранжевых динамических систем на основе итерационной регуляризации работает следующим образом: на первый информационный вход первого блока 1.1 хранения констант (фиг.1) поступает значение наблюдаемой величины; первый информационный выход первого блока 1.1 хранения констант соединен с первым информационным входом первого блока 4.1 формирования произведения; второй, третий и четвертый информационные выходы первого блока 1.1 хранения констант соединены соответственно с первым, вторым и третьим информационными входами первого блока 2.1 формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) ; второй и четвертый информационные выходы первого блока 1.1 хранения констант соединены соответственно с первым и вторым информационными входами второго блока 2.2 формирования функции H ( x ^ i , ( z ^ i ) , t ) ; пятый информационный выход первого блока 1.1 хранения констант соединен со вторыми информационными входами первого блока 8.1, второго блока 8.2, третьего блока 8.3 и шестого блока 8.6 интегрирования, а также с первыми информационными входами четвертого блока 8.4 и пятого блока 8.5 интегрирования; шестой информационный выход первого блока 1.1 хранения констант соединен со вторым информационным входом второго блока 5.2 формирования разности; седьмой информационный выход первого блока 1.1 хранения констант соединен с первым информационным входом третьего блока 2.3 формирования функции (1-γ_i-1); восьмой информационный выход первого блока 1.1 хранения констант соединен со вторым информационным входом третьего блока 2.3 формирования функции (1-γ_i-1) и третьим информационным входом первого блока 6.1 формирования суммы; девятый информационный выход первого блока 1.1 хранения констант соединен со вторым информационным входом третьего блока 4.3 формирования произведения; десятый информационный выход первого блока 1.1 хранения констант соединен с первым и вторым информационными входами соответственно шестого блока 4.6 и девятого блока 4.9 формирования произведения; одиннадцатый информационный выход первого блока 1.1 хранения констант соединен с первым информационным входом второго блока 7.2 транспонирования, а также с первыми информационными входами восьмого блока 4.8 и девятого блока 4.9 формирования произведения; двенадцатый информационный выход первого блока 1.1 хранения констант соединен с первым информационным входом седьмого блока 4.7 формирования произведения; тринадцатый информационный выход первого блока 1:1 хранения констант соединен с первым информационным входом третьего блока 5.3 формирования разности; информационный выход первого блока 2.1 формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) соединен со вторым информационным входом первого блока 5.1 формирования разности, а также с первыми информационными входами второго блока 3.2, третьего блока 3.3 и четвертого блока 3.4 формирования производной; информационный выход второго блока 2.2 формирования функции H ( x ^ i , ( z ^ i ) , t ) соединен с первыми информационными входами первого блока 7.1 транспонирования и второго блока 5.2 формирования разности, информационный выход которого соединен с первым информационным входом второго блока 4.2 формирования произведения, информационный выход которого соединен с первыми информационными входами второго блока 1.2 хранения констант и первого блока 6.1 формирования суммы; информационный выход второго блока 1.2 хранения констант соединен со вторым информационным входом первого блока 6.1 формирования суммы, информационный выход которого соединен с первым информационным входом третьего блока 4.3 формирования произведения, информационный выход которого соединен с первым информационным входом четвертого блока 4.4 формирования произведения; информационный выход первого блока 7.1 транспонирования соединен с первым информационным входом первого блока 3.1 формирования производной, информационный выход которого соединен со вторым информационным входом четвертого блока 4.4 формирования произведения, информационный выход которого соединен соответственно со вторым информационным входом первого блока 4.1 формирования произведения и первыми информационными входами пятого блока 4.5 формирования произведения и пятого блока 3.5 формирования производной, информационный выход которого соединен с первым информационным входом десятого блока 4.10 формирования произведения; информационный выход второго блока 7.2 транспонирования соединен со вторым информационным входом шестого блока 4.6 формирования произведения, информационный выход которого соединен соответственно со вторыми информационными входами пятого блока 4.5 и десятого блока 4.10 формирования произведения, информационный выход которого соединен со вторым информационным входом одиннадцатого блока 4.11 формирования произведения; информационный выход девятого блока 4.9 формирования произведения соединен с первым информационным входом одиннадцатого блока 4.11 формирования произведения, информационный выход которого соединен со вторым информационным входом третьего блока 5.3 формирования разности, информационный выход которого соединен с первым информационным входом шестого блока 8.6 интегрирования, информационный выход которого соединен с первым и вторым информационными входами соответственно шестого блока 4.6 и девятого блока 4.9 формирования произведения; информационный выход первого блока 4.1 формирования умножения соединен с первым информационным входом первого блока 5.1 формирования разности, информационный выход которого соединен с первым информационным входом первого блока 8.1 интегрирования, информационный выход которого соединен со вторым информационным входом первого блока 2.1 формирования функции f(xitihz.i) и первым информационным входом второго блока 8.2 интегрирования, информационный выход которого соединен с первыми информационными входами первого блока 2.1 и второго блока 2.2 формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) и H ( x ^ i , ( z ^ i ) , t ) , соответственно; информационный выход пятого блока 4.5 формирования произведения соединен с первым информационным входом третьего блока 8.3 интегрирования, с информационного выхода которого снимается значение искомого вектора идентификации параметров z и подается на второй и третий информационные входы соответственно второго блока 2.2 и первого блока 2.1 формирования функции H ( x ^ i , ( z ^ i ) , t ) и f ( x ^ i , x ˙ ^ i , z ^ i ) соответственно; информационный выход второго блока 3.2 формирования производной соединен со вторым информационным входом седьмого блока 4.7 формирования произведения, информационный выход которого соединен с первым информационным входом второго блока 6.2 формирования суммы; информационный выход третьего блока 3.3 формирования производной соединен со вторым информационным входом восьмого блока 4.8 формирования произведения, информационный выход которого соединен со вторым информационным входом второго блока 6.2 формирования суммы, информационный выход которого соединен с первым информационным входом третьего блока 6.3 формирования суммы; информационный выход четвертого блока 3.4 формирования производной соединен со вторым информационным входом третьего блока 6.3 формирования суммы, информационный выход которого соединен со вторым информационным входом пятого блока 8.5 интегрирования, информационный выход которого соединен с первым информационным входом седьмого блока 4.7 формирования произведения и вторым информационным входом четвертого блока 8.4 интегрирования, информационный выход которого соединен с первым информационным входом второго блока 7.2 транспонирования, а также с первыми информационными входами восьмого блока 4.8 и девятого блока 4.9 формирования произведения.

Информационный выход первого блока 5.1 формирования разности соединен с первым информационным входом блока 8.1.1 формирования произведения (фиг.2); пятый информационный выход первого блока 1.1 хранения констант соединен со вторым информационным входом первого 8.1 блока интегрирования, информационный выход которого соединен с первым информационным входом блока 8.1.2 формирования суммы; информационный выход линии задержки 8.1.3 соединен со вторым информационным входом блока 8.1.2 формирования суммы, с информационного выхода которого снимается значение первообразной и подается на первый вход линии задержки 8.1.3 и на второй информационный вход первого блока 2.1 формирования функции f ( x ^ i , x ˙ ^ i , z ^ i ) и первый

информационный вход второго блока 8.2 интегрирования.

Блоки 8.2, 8.3, 8.4, 8.5, 8.6 интегрирования (фиг.1) имеют структуру и связи, аналогичные блоку 8.1, рассмотренному выше.

Заявленное изобретение направлено на повышение эффективности идентификации параметров динамических систем, что весьма важно на всех этапах создания, экспериментальной обработки и эксплуатации объектов ракетно-космической, авиационной, корабельной и других видов техники.

Приведенные результаты позволяют утверждать, что идентификация параметров на основе вариационных принципов с использованием итерационной регуляризации обеспечивает увеличение точности оценок в сравнении с известным фильтром Калмана.

Структура предлагаемого устройства определяется решением задачи, чья постановка приведена ниже.

Принято, что динамическая система описывается следующим векторным уравнением дифференциальным уравнением

x ¨ = f ( x , x ˙ , z ) ,   x ( 0 ) = x ∘ ,   x ˙ ( 0 ) = x ∘ ,   ( 1 )

где x∈Rⁿ - вектор обобщенных координат,

x ∈ R n - вектор обобщенных скоростей,

z∈R^m - вектор неизвестных постоянных параметров, подлежащих идентификации,

f - вектор-функция, непрерывная и дифференцируемая по совокупности аргументов,

n, m - натуральные числа,

T∈[0,T].

Уравнение наблюдения имеет вид

y = H ( x , t ) + n ( t ) ,   ( 2 )

где y∈R^k - вектор наблюдения,

H(x, f) - непрерывная вместе с частными производными вектор-функция,

k - натуральное число,

n(t) - вектор белого гауссовского шума.

Пусть динамика идентифицируемых параметров z определяется уравнением

z ˙ = η ,   z ( 0 ) = z ∘ ,   ( 3 )

где η∈R^m - вектор неизвестных неслучайных возмущений, удовлетворяющий требованиям физической реализуемости η ( t ) ∈ L 2 m [ 0, T ] .

Пусть динамика исследуемой системы определяется принципом Гамильтона-Остроградского. В соответствии с ним

δ ' W = δ S + ∫ 0 T δ ' A d t = ∫ 0 T [ δ L + Q δ x ] d t = 0,   ( 4 )

где S - действие по Гамильтону на интервале времени [0, T],

L - кинетический потенциал,

А - работа вектора обобщенных внешних сил Q∈Rⁿ,

δx - вектор вариаций обобщенных координат, знак δ' обозначает бесконечно малую величину, которая не является вариацией.

Ставится задача определения оценки z ^ вектора z из условия минимума функционала невязки

J 1 = 1 2 ∫ 0 T [ y − H ( x ^ ( z ^ ) , t ) ] T N − 1 [ y − H ( x ^ ( z ^ ) , t ) ] d t → min ,   ( 5 )

где N∈R^m×R^m - матрица односторонней спектральной плотности шума наблюдения, характеризующая интенсивность помех в канале наблюдений.

Задача идентификации параметров динамических систем (1)-(5) является обратной, некорректно поставленной по Адамару. Для ее решения используется метод регуляризации А.Н. Тихонова.

Это требует рассмотрения условий минимума сглаживающего функционала

J α [ z , x ] = J 1 + μ W + α Ω [ η ] ,   ( 6 )

где Ω [ η ] = 1 2 ∫ 0 T η T ( t ) η ( t ) d t - стабилизирующий функционал,

α - положительное число.

Функционал J^α[z, х] неотрицательный, поэтому существует его нижняя грань, и если {α_n} - убывающая последовательность положительных чисел, сходящихся к нулю (α→0), и соответствующая последовательность {η_n(t)}, согласно, сходится к η*(t) при условии, что числовой параметр α удовлетворяет требованиям

lim n → ∞ α n = 0,   lim n → ∞ ∑ k = 1 n α k = ∞ ,   lim n → ∞ ∑ k = 1 n α k < ∞ .

Для дифференцируемого выпуклого функционала J^α[z, x] минимум находится путем определения стационарной точки, в которой

g r a d z J α [ z ^ , x ^ ] = g r a n d x J α [ z ^ , x ^ ] = 0,   ( 7 )

при ограничениях (1) - (3).

Для определения градиента в (7) воспользуемся игольчатым варьированием возмущения η(t) и асинхронным варьированием траектории x(t).

Игольчатой вариацией возмущения будем называть функцию вида

η ε ( t ) = { v ,   t ∈ [ τ , τ + ε l ] , v * ( t ) ,   t ∉ [ τ , τ + ε l ] .

где τ - заданная произвольная точка непрерывности функции η*(t),

v - некоторый постоянный вектор,

l -заданное положительное число,

ε - произвольное положительное число, такое, что τ+εl<T.

Разность η_ε(t)-η*(t)=δη(t) будем называть игольчатой вариацией возмущения, которая порождает вариацию параметров δz(t), вызывающую вариацию траектории δx(t). Обозначим x_ε(t) - траекторию, соответствующую η_ε(t), x*(t) - соответствующую Вариацию траектории вида δx_c(t)=x_ε(t)-x*(t) будем называть синхронной, а вариацию

δ x a ( t ) = x ε ( t + d t ) − x * ( t ) = ∂ x ∂ z δ z = G δ z

асинхронной согласно терминологии.

Здесь G - матрица чувствительности системы (1) по вектору параметров z, удовлетворяющая уравнению

G ¨ = ∂ f ∂ x ˙ G ˙ + ∂ f ∂ x G + ∂ f ∂ x ,   G ( 0 ) = G ˙ ( 0 ) = 0

Вариации δx_c(t) и δx_a(t) обладают следующими свойствами

δx_c(t)=0, t∈[0,τ+εl),

δx_c(t)=0, t∉[0,τ+εl),

δx_c(t)=δx_a(t), t+τ+εl.

Пусть η*(t) - возмущение, доставляющее минимум функционалу (6). Найдем приращение функционала (6), обусловленное игольчатой вариацией η_ε(t). Заметим, что на интервале [τ,τ+εl] за счет скачка η_ε(t) возникает асинхронная вариация δx_a(t), а на интервале [τ+εl,T] возникает синхронная δx_c(t), поскольку приращения обобщенных координат

определяются решением дифференциальных уравнений в вариациях при начальных условиях в момент времени t=τ+εl. Таким образом, имеем

Δ J = ∫ τ τ + ε l { [ − ( y − H ( x , t ) ) T N − 1 ∂ H ∂ x ] δ x a + α η T δ η + μ δ L a = Q δ x a } d t + ∫ τ + ε l T { [ − ( y − H ( x , t ) ) T N − 1 ∂ H ∂ x ] δ x c + μ δ L c + Q δ x c } d t ( 8 )

где δL_a и δL_c - вариации кинетического потенциала, связанные соответственное δx_a(t) и δx_c(Y)-

Учитывая, что z ˙ = η , выполняя преобра