Способ измерения угла тангажа летательного аппарата и радионавигационная система для его реализации

Способ измерения угла тангажа летательного аппарата и радионавигационная система для его реализации

Иллюстрации

Показать все

Реферат

Изобретение относится к радионавигации и может использоваться в пилотажно-навигационных системах ориентации летательного аппарата (ЛА) при заходе на посадку по приборам.

Известные способы и устройства измерения угла тангажа ЛА основаны на использовании инерциальных систем навигации, в частности гироскопических систем ориентации [1-4]. Таким способам измерения и устройствам их реализующим присущ ряд недостатков. Во-первых, с течением времени происходит постоянное накапливание ошибки измерений и за один час полета она составляет величину единицы градусов [2, 3]. Во-вторых, если ЛА развивает значительные перегрузки, то происходит увеличение собственной скорости прецессии гироскопа, что в ряде случаев может привести к полной потере его работоспособности [2].

Поскольку известные способы измерения угла тангажа ЛА и устройства их реализующие основаны на другом физическом принципе, по сравнению с заявляемым, то они не могут рассматриваться в качестве аналогов, так как не имеют общих признаков.

Сущность заявляемого способа измерения угла тангажа ЛА заключается в следующем.

Из точки с известными координатами излучают горизонтально линейно-поляризованные электромагнитные волны, вектор напряженности электрического поля E → ˙ которых совпадает с горизонтальной плоскостью (плоскостью горизонта) и совпадает также с положительным направлением оси ОХ, лежащей в этой плоскости, и совместно с осью OY, перпендикулярной к горизонтальной плоскости, образуют неподвижную прямоугольную систему координат YOX.

На борту ЛА приемная антенна, ось симметрии диаграммы направленности которой перпендикулярна направлению движения ЛА, осуществляет боковой прием электромагнитных волн в круговом ортогональном синфазном поляризационном базисе, где происходит разделение (разложение) принятых электромагнитных волн на две ортогонально-поляризованные по кругу составляющие левого E → ˙ L и правого E → ˙ R направлений вращения вектора напряженности электрического поля E → ˙ . После чего измеряют разность фаз между ними Δφ_LR=φ_L-φ_R и по измеренной разности фаз Δφ_LR рассчитывают угол тангажа ξ ЛА между продольной осью ЛА и горизонтальной плоскостью (плоскостью горизонта).

Установим связь между разностью фаз Δφ_LR ортогонально-поляризованных по кругу волн левого E → ˙ L и правого E → ˙ R направлений вращения составляющих вектора электрического поля E → ˙ и углом тангажа ξ ЛА.

Для установления этой связи воспользуемся известным [5-7] формализмом векторов и матриц Джонса.

Поскольку прием электромагнитных волн на борту ЛА производится в собственном круговом поляризационном базисе, где происходит разделение принятых электромагнитных волн на две волны круговой поляризации с противоположным направлением вращения, представим для наглядности излучаемую горизонтально линейно-поляризованную электромагнитную волну в линейном ортогональном поляризационном базисе, единичные орты (векторы) [ e → x , e → y ] которого совпадают соответственно с осями ОХ и OY неподвижной декартовой прямоугольной системы координат YOX, в виде суммы таких волн. Тогда получим:

E → ˙ = [ E ˙ x E ˙ y ] ⋅ e j ϖ t = [ E m x 2 e j ϖ t E m x 2 e j ( ϖ t − π 2 ) ] + [ E m x 2 e j ϖ t E m x 2 e j ( ϖ t + π 2 ) ] ,   ( 1 )

где E ˙ x , E ˙ y - комплексные амплитуды двух проекций электрического поля E → на оси декартовой прямоугольной системы координат YOX,

ω - круговая частота,

t - время.

Анализируя (1), видим, что первая группа составляющих представляет собой электромагнитную волну, поляризованную по кругу с левым направлением вращения E → ˙ L вектора электрического поля, в то время как вторая группа составляющих представляет волну, поляризованную по кругу с правым E → ˙ R направлением вращения вектора электрического поля. При этом необходимо отметить, что направление вращения вектора электрического поля определено с точки зрения наблюдателя, рассматривающего волну против ее распространения. Подставляя в (1) t=0 и E m x =1, а также используя формализм векторов Джонса [5-7], получим выражение для вектора Джонса E → ˙ излучаемых электромагнитных волн в линейном ортогональном поляризационном базисе в виде:

E → ˙ = [ 1 0 ] = 1 2 { [ 1 − j ] + [ 1 j ] } .   ( 2 )

Тогда вектор Джонса принимаемой горизонтально линейно-поляризованной электромагнитной волны (2), заданной своими проекциями в линейном поляризационном базисе суммой двух волн, поляризованных по кругу с противоположным направлением вращения вектора электрического поля, может быть определен на борту ЛА, имеющего отрицательный -ξ или положительный +ξ тангаж, при переходе в круговой синфазный ортогональный поляризационный базис, на входе приемника в виде:

E → ˙ R L = [ E ˙ L E ˙ R ] = 1 2 ⋅ [ 1 j 1 − j ] ⋅ [ cos ξ ± sin ξ ∓ sin ξ cos ξ ] ⋅ E → ˙ ,   ( 3 )

где E → ˙ = 1 2 { [ 1 − j ] + [ 1 j ] } - вектор Джонса E → ˙ излучаемых горизонтально линейно-поляризованных электромагнитных волн, заданный своими проекциями в линейном ортогональном поляризационном базисе в виде суммы двух волн, поляризованных по кругу с противоположным направлением вращения E → ˙ L и E → ˙ R ,

[ cos ξ ± sin ξ ∓ sin cos ξ ] - оператор поворота на произвольный угол тангажа ∓ ξ ,

-ξ соответствует отрицательному углу тангажа ЛА, когда продольная ось находится ниже горизонтальной плоскости (плоскости горизонта),

+ξ соответствует положительному углу тангажа ЛА, когда продольная ось находится выше горизонтальной плоскости (плоскости горизонта),

[ 1 j 1 − j ] - оператор перехода из линейного поляризационного базиса в круговой синфазный поляризационный базис, в котором базисные единичные векторы соответствуют волнам с левой и правой круговыми поляризациями, электрические векторы которых в момент времени t=0 совпадают с направлением вектора напряженности электрического поля E → ˙ .

После преобразований получим аналитические выражения для ортогонально-поляризованных по кругу составляющих левого E ˙ L и правого E ˙ R направлений вращения вектора электрического поля E → на входе приемника в виде:

E ˙ L = 1 2 2 ⋅ [ 1 j 1 − j ] ⋅ [ cos ξ ± sin ξ ∓ sin ξ cos ξ ] ⋅ [ 1 − j ] ,   ( 4 )

E ˙ R = 1 2 2 ⋅ [ 1 j 1 − j ] ⋅ [ cos ξ ± sin ξ ∓ sin ξ cos ξ ] ⋅ [ 1 j ] .   ( 5 )

Подставляя в (4) и (5) значения -ξ, получим соответственно выражения для E ˙ L и E ˙ R на входе приемника в виде:

E ˙ L = 1 2 ( cos ξ − j   sin ξ ) ,   ( 6 )

E ˙ R = 1 2 ( cos ξ + j   sin ξ ) .   ( 7 )

Используя известные соотношения [7], амплитуды A_L и A_R ортогонально-поляризованных по кругу составляющих левого E ˙ L и правого E ˙ R исправлений вращения, а также их фазы φ_L и φ_R на входе приемника имеют вид:

A L = 1 2 ,   ( 8 )

ϕ L = − a r c t g sin ξ cos ξ ,   ( 9 )

A R = 1 2 ,   ( 10 )

ϕ R = a r c t g sin ξ cos ξ ,   ( 11 )

а их разность фаз Δφ_LR после преобразований имеет вид:

Δ ϕ L R = ϕ L − ϕ R = − 2 ξ ,   ( 12 )

откуда следует, что

ξ = − Δ ϕ L R 2 .   ( 13 )

Из анализа (8) и (10) следует, что амплитуды A_L и A_R составляющих E ˙ L и E ˙ R на входе приемника равны между собой A_L=A_R и не зависят от угла тангажа ξ ЛА. В то же время из анализа (12) видно, что наличие фазового сдвига Δφ_LR между ортогонально-поляризованными по кругу составляющими левого E ˙ L и правого E ˙ R направлений вращения обусловлено углом тангажа ξ ЛА.

Аналогично, подставляя в (4) и (5) значения +ξ, получим выражения для E ˙ L и E ˙ R на входе приемника в виде:

E ˙ L = 1 2 ( cos ξ + j   sin ξ ) ,   ( 14 )

E ˙ R = 1 2 ( cos ξ − j   sin ξ ) .   ( 15 )

Соответственно амплитуды A_L и A_R, а также фазы φ_L и φ_R составляющих E ˙ L и E ˙ R на входе приемника имеют вид:

A L = 1 2 ,   ( 16 )

ϕ L = a r c t g sin ξ cos ξ ,   ( 17 )

A R = 1 2 ,   ( 18 )

ϕ R = − a r c t g sin ξ cos ξ ,   ( 19 )

а их разность фаз Δφ_LR имеет вид:

Δ ϕ L R = ϕ L − ϕ R = 2 ξ ,   ( 20 )

откуда следует, что

ξ = − Δ ϕ L R 2 .   ( 21 )

Из анализа (6) и (18) следует, что амплитуды A_L и A_R составляющих E ˙ L и E ˙ R для положительных углов тангажа +ξ также равны между собой A_L=A_R и не зависят от угла тангажа ξ ЛА. В то же время разность фаз Δφ_LR (20) определяется углом тангажа ξ ЛА. Сравнивая (13) и (21), окончательно имеем выражение для определения угла тангажа ξ ЛА в виде:

ξ [ г р а д ] = ± Δ ϕ L R 2 [ г р а д ] ,   ( 22 )

где «+» соответствует положительному углу тангажа ξ, когда продольная ось ЛА находится выше горизонтальной плоскости,

«-» соответствует отрицательному углу тангажа ξ, когда продольная ось ЛА находится ниже горизонтальной плоскости,

Δφ_LR=φ_L-φ_R - разность фаз между ортогонально-поляризованными по кругу составляющими E ˙ L и E ˙ R .

Проводя сравнительный анализ (12) и (20), видим, что при появлении угла тангажа ЛА возникает одновременно фазовый сдвиг Δφ_LR между ортогонально-поляризованными по кругу составляющими левого E ˙ L и правого E ˙ R направлений вращения на входе приемной антенны, что неизменно приводит к изменению угла ориентации вектора напряженности электрического поля E → принимаемых на борту ЛА электромагнитных волн или, иначе говоря, одновременно изменяется ориентация плоскости поляризации принимаемых электромагнитных волн. Последнее обуславливает физическую основу определения угла тангажа ЛА по измеренной на выходе приемника разности фаз Δφ_LR между ортогонально-поляризованными по кругу составляющими E ˙ L и E ˙ R .

Использование заявляемой совокупности признаков для измерения угла тангажа ЛА в известных решениях автором не обнаружено.

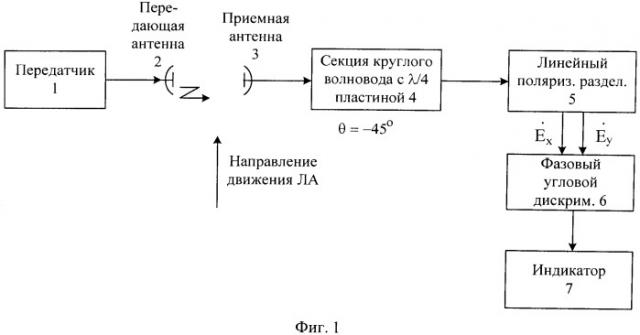
На фиг.1 представлена структурная электрическая схема радионавигационной системы, реализующей предложенный способ измерения угла тангажа ЛА.

Радионавигационная система содержит передатчик 1 и передающую антенну 2, расположенные в точке с известными координатами. На борту ЛА радионавигационная система содержит приемную антенну 3, секцию круглого волновода с встроенной внутрь четвертьволновой фазовой пластиной 4, линейный поляризационный разделитель 5, фазовый угловой дискриминатор 6 и индикатор 7.

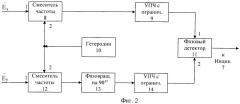
На фиг.2 представлена структурная электрическая схема фазового углового дискриминатора 6, включающего в себя первый и второй смесители частоты 8 и 12, первый усилитель промежуточной частоты (УПЧ) с ограничением по амплитуде 9, гетеродин 10, фазовращатель на 90° 13, второй усилитель промежуточной частоты (УПЧ) с ограничением по амплитуде 14 и фазовый детектор 11.

Радионавигационная система работает следующим образом.

Передатчик 1 через передающую антенну 2 с горизонтальной собственной поляризацией излучает в направлении ЛА горизонтально линейно-поляризованные электромагнитные волны, вектор напряженности электрического поля E → которых совпадает с горизонтальной плоскостью (плоскостью горизонта) и задан своими проекциями в линейном ортогональном поляризационном базисе суммой двух волн, ортогонально-поляризованных по кругу, в виде (2). При этом единичные орты (векторы) [ e → x , e → y ] линейного ортогонального поляризационного базиса совпадают с горизонтальной плоскостью и перпендикуляром к этой плоскости соответственно.

На борту ЛА приемная антенна 3, ось симметрии диаграммы направленности которой перпендикулярна направлению движения ЛА, принимает электромагнитные волны, вектор Джонса которых имеет вид (2), после чего сигнал поступает на последовательно соединенные секцию круглого волновода с встроенной внутрь четвертьволновой фазовой пластиной 4 и линейный поляризационный разделитель 5, выполненный в виде перехода с круглого волновода на два ортогонально расположенных по отношению друг к другу прямоугольных волноводов, орты собственной системы координат которого совпадают с осями плеч прямоугольных волноводов и совпадают также с вертикальной и продольной осями ЛА соответственно. Причем четвертьволновая фазовая пластина ориентирована под углом θ=-45° к одной из стенок прямоугольного волновода линейного поляризационного разделителя 5. Сочетание секции круглого волновода с встроенной внутрь четвертьволновой фазовой пластиной 4 и линейного поляризационного разделителя 5 позволяет, как известно [7, 8], осуществить на борту ЛА прием электромагнитных волн в круговом поляризационном базисе и, таким образом, разделить поступающие на вход электромагнитные волны, вектор Джонса которых задан в виде (2), на две ортогонально-поляризованные по кругу составляющие левого E → L и правого E → R направлений вращения вектора электрического поля E → ˙ и преобразовать их на выходах линейного поляризационного разделителя 5 со стороны ортогонально расположенных прямоугольных волноводов в ортогонально линейно-поляризованные сигналы E ˙ x и E ˙ y соответственно. В этом случае сигналы на выходах плеч линейного поляризационного разделителя 5 определяются с помощью преобразований вида:

E ˙ x = [ 1 0 0 0 ]   [ cos θ sin θ − sin θ cos θ ]   [ 1 0 0 j ]   [ cos θ − sin θ sin θ cos θ ]   [ cos ξ ± sin ξ ∓ sin ξ cos ξ ] ⋅ E → ,   ( 23 )

E ˙ y = [ 0 0 0 1 ]   [ cos θ sin θ − sin θ cos θ ]   [ 1 0 0 j ]   [ cos θ − sin θ sin θ cos θ ]   [ cos ξ ± sin ξ ∓ sin ξ cos ξ ] ⋅ E → ,   ( 24 )

где E → ˙ = 1 2 { [ 1 − j ] + [ 1 j ] } - вектор Джонса E → ˙ излучаемых горизонтально линейно-поляризованных электромагнитных волн, заданный своими проекциями в линейном ортогональном поляризационном базисе [ e → x , e → y ] в виде суммы двух волн, ортогонально-поляризованных по кругу составляющих левого E → ˙ L и правого E → ˙ R направлений вращения,

[ cos ξ ± sin ξ ∓ sin ξ cos ξ ] - оператор поворота на произвольный угол тангажа ∓ ξ ,

[ cos θ − sin θ sin θ cos θ ] - оператор прямого перехода из опорной неподвижной прямоугольной системы координат YOX, в котором записан вектор Джонса E → излучаемых горизонтально линейно-поляризованных электромагнитных волн в собственную систему координат четвертьволновой фазовой пластины λ/4 (θ - угол ориентации четвертьволновой фазовой пластины, λ - длина волны),

[ 1 0 0 j ] - оператор Джонса четвертьволновой фазовой пластины, записанный в собственной системе координат, в которой он имеет диагональный вид,

[ cos θ sin θ − sin θ cos θ ] - оператор обратного перехода из собственной системы координат четвертьволновой фазовой пластины λ/4 в опорную неподвижную прямоугольную систему координат YOX, в которой представлен вектор Джонса E → излучаемых электромагнитных волн,

[ 1 0 0 0 ] - оператор первого плеча линейного поляризационного разделителя, собственный орт которого совпадает с продольной осью ЛА,

[ 0 0 0 1 ] - оператор второго плеча линейного поляризационного разделителя, собственный орт которого совпадает с вертикальной осью ЛА.

Подставляя в (23) и (24) значения -ξ и θ=-45° и проделав необходимые матричные преобразования, получим аналитические выражения для ортогонально линейно-поляризованных сигналов E → ˙ x и E → ˙ y на выходах линейного поляризационного разделителя 5 вида:

E ˙ x = 1 2 { ( cos ξ + sin ξ ) + j ( cos ξ − sin ξ ) } ,   ( 25 )

E ˙ y = 1 2 { − ( cos ξ + sin ξ ) + j ( cos ξ − sin ξ ) } .   ( 26 )

Уместно пояснить суть полученных выражений (25) и (26). Для этого обратимся к соотношению (2), из которого следует, что вектор Джонса E → ˙ излучаемых горизонтально линейно-поляризованных электромагнитных волн, представленный своими проекциями в линейном ортогональном поляризационном базисе в виде суммы двух волн, ортогонально поляризованных по кругу с левым E → ˙ L и правым E → ˙ R направлениями вращения вектора электрического поля, принимается на борту ЛА приемной антенной 2 и поступает на вход секции круглого волновода с встроенной внутрь четвертьволновой фазовой пластиной. При прохождении этой секции ортогонально-поляризованные по кругу электромагнитны