Способ возбуждения механических колебаний силовых факторов с прогнозируемыми параметрами

Способ возбуждения механических колебаний силовых факторов с прогнозируемыми параметрами

Иллюстрации

Показать все

Реферат

Изобретение относится к вибрационной технике, в частности к технике агропромышленного комплекса, и может быть использовано на зерноперерабатывающих предприятиях в технологическом и транспортном оборудовании. Кроме того, изобретение может быть использовано в других отраслях промышленности, связанных с переработкой сыпучих материалов.

Цель изобретения - совершенствование оборудования для сепарирования и транспортирования зерна и других сыпучих материалов путем сообщения рабочим органам машин колебаний с параметрами, соответствующими осуществляемому процессу.

Известны способы возбуждения механических колебаний силовых факторов (силы и/или момента) с применением центробежных вибровозбудителей. При этом вибровозбудитель может содержать один или несколько дебалансов. Дебаланс представляет собой вращающееся неуравновешенное звено. Дисбалансом дебаланса называют произведение неуравновешенной массы m на ее эксцентриситет r относительно оси вращения.

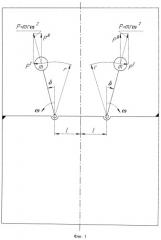
Известен способ возбуждения прямолинейных гармонических колебаний силы [1] центробежным вибровозбудителем (фиг.1), содержащим два дебаланса, имеющих одинаковые дисбалансы, вращающихся вокруг параллельных осей. Оси вращения дебалансов расположены на общем основании. Дебалансы равномерно вращаются с одинаковыми по величине угловыми скоростями в противоположных направлениях. Вращение дебалансов должно быть синхронизировано и согласовано по фазе, так чтобы в любой произвольный момент времени дебалансы располагались симметрично относительно прямой, проходящей перпендикулярно через средину отрезка, соединяющего оси вращения дебалансов. Это достигается соответствующей начальной фазировкой дебалансов и вращением их с одинаковыми по величине угловыми скоростями в противоположных направлениях. Следует заметить, что наиболее простой и легко реализуемой на практике является начальная фазировка, при которой развиваемые дебалансами центробежные силы инерции направлены либо перпендикулярно прямой, соединяющей оси вращения дебалансов, в одну сторону, либо вдоль этой прямой в противоположные стороны.

С целью объяснения возникновения прямолинейно колеблющейся по гармоническому закону силы рассмотрим некоторое произвольное положение дебалансов (фиг.1). На рисунке (фиг.1) показано положение дебалансов после их поворота из начального положения на некоторый произвольный угол δ. Заметим, что за начальное положение дебалансов принято такое положение, при котором центробежные силы инерции дебалансов направлены перпендикулярно прямой, соединяющей оси их вращения. Представим силу инерции каждого дебаланса в виде двух составляющих: вертикальная составляющая - P^B=mrω²cosδ; горизонтальная составляющая - P^г=mrω²sinδ. Как видно из рисунка, горизонтальные составляющие сил инерции дебалансов направлены вдоль одной прямой в противоположных направлениях, а значит уравновешивают друг друга. Вертикальные составляющие, складываясь, образуют результирующую, равную P_Σ=2mrω²cosδ. Результирующая направлена вдоль прямой, проходящей перпендикулярно через середину отрезка, соединяющего оси вращения дебалансов. Таким образом, результирующая сил инерции дебалансов представляет собой прямолинейно колеблющуюся по гармоническому закону силу. Следует заметить, что двухдебалансный центробежный вибровозбудитель может создать силу, прямолинейно колеблющуюся по гармоническому закону, если вращение дебалансов синхронизировано и согласовано по фазе так, что в каждый момент времени дебалансы расположены симметрично относительно прямой, проходящей перпендикулярно через средину отрезка, соединяющего оси вращения дебалансов. Такие условия синхронизации и согласованности вращения дебалансов достигаются при выполнении следующих условий: начальным положением дебалансов может быть выбрано любое положение, при котором они расположены симметрично относительно прямой, проходящей перпендикулярно через средину отрезка, соединяющего оси вращения дебалансов; дебалансы вращаются с угловыми скоростями, одинаковыми по величине и противоположными по направлению.

Следует заметить, что развиваемая таким вибровозбудителем гармонически колеблющаяся сила может вызвать прямолинейные гармонические колебания основания, а следовательно, и связанного с ним рабочего органа машины, только в том случае, если ось симметрии дебалансов, вдоль которой сила совершает колебания, проходит через центр масс колеблемой системы.

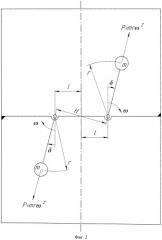
Известен способ возбуждения гармонических колебаний момента [1] центробежным вибровозбудителем, содержащим два одинаковых дебаланса, вращающихся антифазно вокруг параллельных осей (фиг.2). На рисунке (фиг.2) показано произвольное положение дебалансов после их поворота из начального положения на произвольный угол δ. Оси вращения дебалансов расположены на общем основании. Дебалансы вращаются с постоянными одинаковыми по величине и направлению угловыми скоростями. Заметим, что вращение дебалансов антифазно означает: в любом произвольном положении дебалансов развиваемые ими центробежные силы инерции равны друг другу по величине и направлены в противоположные стороны, то есть образуют пару сил. В представленном на рисунке (фиг.2) положении дебалансов развиваемые ими силы инерции образуют пару сил, момент которой равен М=Р×H=2lmrω²cosδ.

Следует заметить, что создаваемая таким центробежным вибровозбудителем пара сил может сообщить гармонические вращательные колебания основанию, а следовательно, и связанному с ним рабочему органу машины, вокруг оси перпендикулярной плоскости действия пары сил и проходящей через центр масс колеблемой системы в том случае, если оси вращения дебалансов расположены симметрично относительно плоскости, перпендикулярной плоскости действия пары и проходящей через центр масс колеблемой системы. На фигуре 2 осевой линией показана линия пересечения таких взаимно перпендикулярных плоскостей.

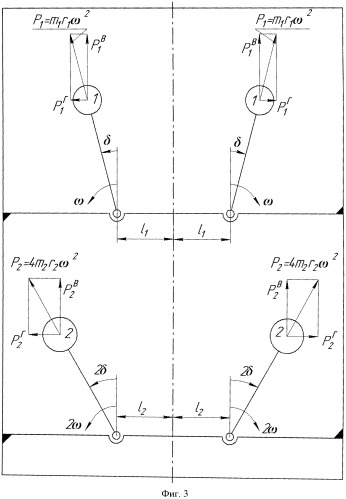
Наиболее близким по технической сущности и достигаемому результату является способ возбуждения негармонических колебаний силы [2] центробежным вибровозбудителем, содержащим четыре дебаланса, вращающиеся вокруг параллельных осей (фиг.3). Оси вращения дебалансов расположены на общем основании. Дебалансы вращаются равномерно и попарно имеют одинаковые по величине угловые скорости противоположного направления. При этом величина угловой скорости первой пары дебалансов вдвое меньше величины угловой скорости второй пары дебалансов, то есть первая пара дебалансов вращается с угловой скоростью ω, а вторая с угловой скоростью - 2ω. Дебалансы, вращающиеся с равными по величине угловыми скоростями, имеют одинаковые дисбалансы, то есть одинаковые по величине произведения неуравновешенной массы m на ее эксцентриситет r относительно оси вращения. Причем дисбалансы дебалансов, вращающихся с частотой 2ω в четыре раза меньше величины дисбалансов дебалансов, вращающихся с частотой ω. Для упрощения дальнейших рассуждений условимся называть одноименными дебалансы, вращающиеся с равными по величине угловыми скоростями, а отрезок, соединяющий оси таких дебалансов, межосевым расстоянием одноименных дебалансов. Оси вращения одноименных дебалансов расположены симметрично относительно прямой перпендикулярной межосевому расстоянию. При этом оси вращения первой пары дебалансов и оси вращения второй пары дебалансов расположены симметрично относительно одной и той же прямой. На рисунке (фиг.3) показано некоторое произвольное положение дебалансов после поворота из начального положения первой пары дебалансов на угол δ, второй пары - на угол 2δ. Как видно из рисунка, горизонтальные составляющие сил инерции одноименных дебалансов взаимно уравновешивают друг друга. Вертикальные составляющие сил инерции дебалансов, складываясь, образуют результирующую силу P=2m₁r₁ω²cosδ+8m₂r₂ω²cos2δ. Таким образом, создается сила, меняющаяся по негармоническому закону, направленная вдоль прямой, представляющей собой ось симметрии расположения осей вращения дебалансов.

Следует заметить, что такая сила способна сообщить основанию и связанному с ним рабочему органу машины прямолинейные негармонические колебания в том случае, если сила проходит через центр масс колеблемой системы.

Этот способ возбуждения колебаний силы реализован в конструкции машин с целью сообщения рабочему органу несимметричных прямолинейных колебаний. Несимметричность закона колебаний означает неравенство наибольшего положительного значения ускорения рабочего органа модулю наибольшего отрицательного значения ускорения.

Использование известных способов сообщения рабочим органам оборудования для переработки зерна таких видов движения как прямолинейные колебания, вращательные колебания или вращательно колебательного движения с различными кинематическими параметрами связано с необходимостью разработки и создания различных конструкций приводных устройств.

Реализация предлагаемого способа возбуждения колебаний силовых факторов с прогнозируемыми параметрами в конструкциях оборудования для переработки зерна позволит создать унифицированный привод, позволяющий в зависимости от его настройки обеспечивать различный вид движения с возможностью варьирования закона движения.

Известно, что одной из причин направленного в среднем движения частиц сыпучего тела по горизонтальной опорной поверхности, совершающей горизонтальные колебания, является несимметрия закона колебаний поверхности, выражающаяся в том, что наибольшее значение ускорения опорной поверхности в одном из направлений отличается по абсолютной величине от наибольшего значения ускорения в противоположном направлении. Величина средней скорости транспортирования частиц сыпучего тела относительно колеблющейся поверхности, при прочих одинаковых условиях (амплитуда и частота колебаний опорной поверхности, коэффициент трения частиц по поверхности), зависит насколько наибольшее положительное значение ускорения плоскости отличается по модулю от наибольшего отрицательного значения ее ускорения.

Средняя скорость виброперемещения является основным параметром, определяющим производительность транспортного оборудования, а в сепарирующем оборудовании - производительность и эффективность, осуществляемого в этом оборудовании процесса. Средняя скорость виброперемещения влияет на эффективность процесса сепарирования через толщину слоя сыпучего материала и время его пребывания на рабочем органе. При неизменной длине рабочего органа (например, длина сита) увеличение средней скорости частиц сыпучего тела уменьшает время протекания процесса сепарирования и толщину слоя. Уменьшение времени сепарирования снижает эффективность процесса. Уменьшение толщины сыпучего тела до определенного предела, как правило, повышает эффективность процесса сепарирования. Дальнейшее уменьшение толщины слоя ниже определенного значения приводит к снижению эффективности сепарирования.

Следовательно, в транспортном оборудовании, для увеличения его производительности, транспортирующему рабочему органу необходимо сообщать несимметричный закон колебаний с наибольшим различием по абсолютной величине максимальных положительного и отрицательного значений ускорения.

На эффективность ситового сепарирования влияют многочисленные факторы. Отметим некоторые из них: размеры и форма ситового канала; способ очистки сита; кинематический режим рабочего органа.

Действие вибраций на сыпучее тело проявляется в разрыхлении и самосортировании этого тела, с одной стороны, и в подаче, обеспечивающей непрерывность процесса, - с другой. Иногда эффективность процесса сепарирования определяется преимущественно самосортированием. Примерами таких процессов могут служить очистка зерна от равновеликой минеральной примеси в камнеотделительных машинах; процесс ситового сепарирования, в котором проходового компонента немного, а толщина сыпучего тела во много раз больше размеров частиц, то через сито просеиваются лишь частицы, находящиеся в нижнем слое, в который они попадают в результате самосортирования. Если концентрация проходового компонента в исходной смеси велика, как, например, при очистке зерна от крупных примесей в сепараторе или при ситовом сепарировании зерносмесей с большой концентрацией мелкой фракции, то самосортирование не оказывает большого влияния на результаты процесса в целом и решающее значение приобретает просеивание. Самосортирование может снижать эффективность процесса сепарирования в целом. Например, при ситовом сепарировании мелкие частицы с меньшей плотностью, чем у крупных, всплывают в верхние слои зернового потока, удаляясь от сита, что уменьшает количество прохода.

Согласно вышеизложенному в сепарирующих машинах несимметрия закона колебаний рабочего органа должна соответствовать виду осуществляемого в машине процесса. В случае необходимости закон колебаний рабочего органа должен обеспечивать эффективное самосортирование зерносмеси. Эффективность самосортирования находится в прямой зависимости от продолжительности воздействия вибраций на сыпучее тело. Создать такие условия можно обеспечив требуемую несимметрию закона колебаний, то есть обеспечив необходимое различие по абсолютной величине между максимальными положительным и отрицательным значениями ускорения опорной поверхности рабочего органа. Заметим, что на эффективность самосортирования влияет также и интенсивность воздействия вибраций, которая определяется абсолютной величиной ускорения опорной поверхности. С увеличением ускорения интенсивность воздействия увеличивается.

Наиболее рациональными с точки зрения уменьшения габаритов, массы и динамических нагрузок привода являются сепараторы с рабочими органами кольцевой формы, совершающими либо вращательные колебания, либо вращательно колебательное движение вокруг центральной вертикальной оси. Сепараторы не требуют уравновешивания сил инерции рабочего органа вследствие неподвижности его центра масс. Кроме того, при осуществлении в таком сепараторе процесса ситового сепарирования при вращательно колебательном движении рабочего органа достаточно просто может быть обеспечена эффективная очистка ситовой поверхности от застрявших частиц зерновой смеси.

Задача изобретения - совершенствование оборудования для транспортирования и сепарирования зерновых смесей путем сообщения рабочим органам машин движения того вида, который соответствует осуществляемому в оборудовании процессу.

Поставленная задача решается предлагаемым способом возбуждения колебаний силовых факторов (силы или момента) центробежным вибровозбудителем, состоящим из четырех дебалансов, оси вращения которых расположены на общем основании, попарно имеющих одинаковые дисбалансы, определенную фазировку и вращающихся равномерно с одинаковыми по величине угловыми скоростями, что обеспечивается передачей синхронизирующей и согласовывающей по фазе вращение дебалансов с передаточным отношением, равным отношению угловой скорости быстровращающихся дебалансов к угловой скорости медленновращающихся, в котором, согласно изобретению, возбуждение колебаний силовых факторов с прогнозируемыми параметрами достигается соответствующей фазировкой дебалансов, передаточным отношением передачи синхронизирующей и согласовывающей по фазе вращение дебалансов и соотношением максимальных силовых факторов, развиваемых силами инерции медленно- и быстровращающихся дебалансов.

Техническим результатом является варьирование скорости транспортирования и повышение технологической эффективности процессов сепарирования зерновых смесей.

Для сообщения рабочим органам машин колебаний с параметрами, соответствующими осуществляемому процессу, применим центробежный вибровозбудитель с четырьмя дебалансами.

Дисбалансы, то есть произведения неуравновешенной массы m на ее эксцентриситет r относительно оси вращения, двух дебалансов одной пары должны быть равны друг другу. Эти дебалансы должны иметь одинаковые по величине частоты вращения ω. Дисбалансы второй пары дебалансов также должны быть равны друг другу и могут отличаться по величине от дисбалансов первой пары дебалансов. Дебалансы второй пары должны иметь одинаковые по величине частоты вращения, но отличающиеся от частоты вращения первой пары дебалансов. Для определенности введем нумерацию дебалансов. Будем считать первой парой дебалансов дебалансы, вращающиеся с частотой ω₁=ω, а второй парой - с частотой ω₂=nω, n - любое действительное число. Для определенности будем считать, что n>1, то есть, что вторая пара дебалансов вращается с большей частотой. Вращение дебалансов должно быть соответствующим образом синхронизировано и согласовано по фазе. Добиться этого можно посредством либо зубчатой (шестеренной) передачи, либо зубчатой ременной передачи. Заметим, что отношение является передаточным отношением передачи, обеспечивающей согласование по фазе и синхронизацию вращения первой и второй пар дебалансов.

Такой вибровозбудитель позволяет получать различные законы изменения возмущающих силовых факторов (сил или моментов). Эти силовые факторы, в зависимости от конструктивного исполнения (расположения) вибровозбудителя, либо передаются на рабочий орган, либо на выходное звено исполнительного механизма, связанное с рабочим органом.

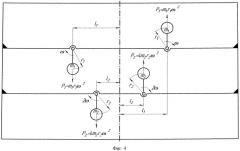
Рассмотрим такое условие начальной фазировки дебалансов, при котором центробежные силы инерции одноименных дебалансов направлены в противоположные стороны вдоль параллельных прямых, отстоящих друг от друга на некотором расстоянии, то есть создают пару сил (момент). Сначала рассмотрим случай, когда дебалансы первой и второй пар вращаются с угловыми скоростями, отличающимися вдвое, то есть передаточное отношение n=2.

На фигуре 4 показано положение дебалансов, при котором центробежные силы инерции одноименных дебалансов параллельны друг другу и направлены в противоположные стороны перпендикулярно прямой, соединяющей оси вращения дебалансов. Заметим, что вследствие равенства этих сил они образуют пару сил, то есть создают момент, действующий на основание, на котором расположены оси вращения дебалансов. В рассматриваемом случае силы инерции первой и второй пар дебалансов создают моменты одинакового направления, а оси вращения одноименных дебалансов расположены симметрично относительно одной и то же прямой.

В соответствии с принятой нумерацией обозначим массу и эксцентриситет каждого дебаланса первой пары соответственно m₁ и r₁, второй пары - m₂ и m₂. Расстояние от осей вращения первой и второй пар дебалансов до прямой, относительно которой оси вращения расположены симметрично, обозначим соответственно l₁ и l₂. При вращении дебалансов возникают центробежные силы инерции. Сила инерции первого дебаланса P₁=m₁r₁ω², сила инерции второго дебаланса Р₂=4m₂r₂ω². Соотношения между массами m₁ и m₂ дебалансов, их эксцентриситетами r₁ и r₂ могут быть различными. Следовательно, могут быть различны соотношения между величинами сил инерции P₁ и P₂ первой и второй пары дебалансов. Например, если m₁=m₂=m и r₁=r₂=r, то сила инерции P₂ в четыре раза больше силы P₁. В том случае, если m₁=m, m₂=0,25m и r₁=r₂=r, то P₁=Р₂. Очевидно, что могут быть созданы условия, при которых будет выполняться условие P₁>P₂. Следует заметить, что варьировать соотношением величин сил инерции P₁ и P₂ следует, варьируя величины m₁, m₂, r₁ и r₂. Соотношение частот вращения первой и второй пар дебалансов один к двум должно сохраняться. Из соотношения частот вращения дебалансов следует, что при повороте первого дебаланса вокруг своей оси вращения на полный оборот второй дебаланс поворачивается вокруг своей оси на два оборота. При вращении дебалансов меняется величина плеча пары сил, следовательно величина момента. Максимальный по величине момент силы инерции одноименных дебалансов создают в том случае, если они направлены перпендикулярно прямой, соединяющей оси вращения дебалансов. Следует заметить, что в рассматриваемом случае силы инерции одноименных дебалансов одновременно создают максимальные по величине моменты одинакового направления. Будем считать это положение дебалансов начальным. Заметим, что максимальная величина момента от сил инерции каждой пары дебалансов зависит как от величины самой силы, так и от максимальной величины плеча пары сил, то есть от расстояния между осями вращения дебалансов. Для первой пары дебалансов максимальная величина плеча равна 2l₁, для второй - 2l₂. Соотношения размеров l₁ и l₂ зависят от расположения осей вращения дебалансов на основании и могут быть следующими: l₁<l₂; l₁=l₂ и l₁>l₂. Следовательно, соотношения между максимальными величинами моментов сил инерции первой и второй пар дебалансов могут быть различными.

Рассмотрим некоторое произвольное положение дебалансов (фиг.5). Произвольное положение дебалансов соответствует повороту из начального положения дебалансов первой пары на произвольный угол δ, а дебалансов второй пары на угол nδ=2δ. Следует заметить, что углы поворота дебалансов связаны между собой передаточным отношением передачи, синхронизирующей и согласовывающей по фазе вращение дебалансов. Запишем выражение результирующего момента, создаваемого центробежными силами инерции дебалансов, в функции углов их поворота. Момент сил инерции первой пары дебалансов

Момент сил инерции второй пары дебалансов

Результирующий момент

Рассмотрим различные сочетания соотношений величин максимальных моментов от сил инерции первой и второй пар дебалансов и определим безразмерные значения экстремумов зависимости результирующих моментов сил инерции дебалансов и оценим степень несимметрии зависимости результирующего момента от угла поворота дебалансов за кинематический цикл вибровозбудителя. Заметим, что кинематическим циклом вибровозбудителя является интервал времени, по истечении которого дебалансы возвращаются в начальное положение.

Определение экстремумов зависимости результирующего момента проведено при следующих значениях соотношения : 0,125 и диапазоне значений от 0,25 до 2,5 с шагом изменения соотношения, равным 0,25.

В качестве примера рассмотрим определение экстремумов зависимости результирующего момента для нескольких значении соотношения .

Пусть m₁=m₂=m, r₁=r₂=r и l₂=2l₁=2l. Тогда выражение результирующего момента имеет вид

Запишем результирующий момент в безразмерном выражении

Исследуем функцию момента от угла поворота дебалансов на экстремумы. Для этого обозначим

Производная функции имеет вид

После преобразований и приравнивания производной нулю, имеем

Последнее уравнение обращается в ноль, если

и

Производная u′(δ) функции u(δ) в течение цикла работы механизма равна нулю при следующих значениях угла δ поворота дебалансов: δ₁=0°, δ₂=91,79°, δ₃=180°, δ₄=268,21° и δ₅=360°. Следует заметить, что функция u(δ) периодическая и в следующем цикле зависимость результирующего момента от угла поворота дебалансов повторяется. Точки δ₁, δ₂, δ₃, δ₄ и δ₅ являются критическими точками функции u(δ). В окрестности точки δ₁ производная меняет знак с плюса на минус, то есть в точке δ₁ функция u(δ) имеет максимум. В окрестности точки δ₂ производная меняет знак с минуса на плюс, то есть в точке δ₂ функция u(δ) имеет минимум. В окрестности точки δ₃ производная меняет знак с плюса на минус. В этом случае в точке δ₃ функция u(δ) имеет максимум. В окрестности точки δ₄ производная меняет знак с минуса на плюс, то есть в точке δ₄ функция u(δ) имеет минимум. В окрестности точки δ₅ производная знак с плюса на минус. В этом случае в точке δ₅ функция u(δ) имеет максимум. Таким образом, функция u(δ) в точках, δ₃ и δ₅ имеет максимумы, а в точках δ₂ и δ₃ - минимумы. Следовательно, зависимость результирующего момента, создаваемого силами инерции дебалансов, от угла поворота дебалансов в течение цикла работы механизма в трех положениях дебалансов имеет максимумы и в двух положениях - минимумы.

Вычислим экстремальные значения функции u(δ)=cosδ+8cos2δ. Результаты расчетов представлены в таблице 1.

Таблица 1
δ, град	u(δ)=cosδ+8cos2δ
0	9
91,79	-8,02
180	7
268,21	-8,02
360	9

Как видно из таблицы 1 функция u(δ)=cosδ+8cos2δ имеет наибольшее значение, равное девяти и наименьшее - минус восемь целых две сотых. В приложении к исследованию значений момента, создаваемого силами инерции дебалансов, это означает, что наибольшие значения момента в противоположных направлениях не равны друг другу. Заметим, что при принятом положительном и отрицательном направлениях момента абсолютная величина наибольшего значения момента в положительном направлении больше абсолютной величины наибольшего значения момента в отрицательном направлении, то есть имеет место несимметрия момента, создаваемого силами инерции дебалансов. Степень несимметрии зависимости результирующего момента от угла поворота дебалансов оценим показателем, характеризующим насколько абсолютная величина наибольшего значения момента в положительном направлении больше абсолютной величины его наибольшего значения в отрицательном направлении в процентах. Таким образом, степень несимметрии зависимости результирующего момента равна

В рассмотренном выше случае, сила инерции Р₂ в четыре раза больше силы инерции P₁, а максимальная величина момента М₂ в восемь раз больше максимальной величины момента M₁, то есть . На рисунке (фиг.6) представлен график функции u(δ)=cosδ+8cos2δ, то есть график зависимости результирующего момента от сил инерции дебалансов в безразмерном выражении от угла поворота дебалансов за цикл работы механизма при .

Рассмотрим случай когда m₁=m₂=m, r₁=r₂=r и l₁=l₂=l. В этом случае соотношение сил инерции P₁ и Р₂ сохраняется, а максимальное значение момента М₂ в четыре раза больше максимального значения момента M₁, то есть .

Зависимость результирующего момента от угла поворота дебалансов в безразмерном выражении запишем в виде

Исследуем функцию u(δ)=cosδ+4cos2δ на экстремумы. Производная функции u(δ) имеет вид

После приравнивания производной нулю и преобразований имеем

Последнее уравнение обращается в ноль, если

и

Производная u′(δ) функции u(δ) в течение цикла работы механизма равна нулю при следующих значениях угла δ поворота дебалансов: δ₁=0°, δ₂=93,58°, δ₃=180°, δ₄=266,42° и δ₅=360°. Точки δ₁, δ₂, δ₃, δ₄ и δ₅ являются критическими точками функции u(δ). Определение знака производной в окрестностях критических точек свидетельствует о том, что функция u(δ) имеет следующие экстремумы: в точке δ₁ - максимум; в точке δ₂ - минимум; в точке δ₃ - максимум; в точке δ₄ - минимум; в точке δ₅ - максимум.

Вычислим экстремальные значения функции u(δ)=cosδ+4cos2δ. Результаты вычислений представлены в таблице 2.

Таблица 2
δ, град	u(δ)=cosδ+4cos2δ
0	5
93,58	-4,03
180	3
266,42	-4,03
360	5

Степень несимметрии зависимости результирующего момента от угла поворота дебалансов составляет

На рисунке (фиг.7) представлен график зависимости результирующего момента сил инерции дебалансов в безразмерном выражении от угла поворота дебалансов за цикл работы механизма при .

Рассмотрим случай когда m₁=2m, m₂=m, r₁=r₂=r, l₁=4l, l₂=l. Тогда момент сил инерции первой пары дебалансов равен

Момент сил инерции второй пары дебалансов

Как видно из уравнений (18) и (19), максимальное значение момента сил инерции первой пары дебалансов в два раза больше максимального значения момента второй пары дебалансов, то есть .

Результирующий момент в безразмерном выражении запишем в виде

Исследуем функцию u(δ)=8cosδ+4cos2δ на экстремумы. Производная функции имеет вид

После приравнивания производной нулю и преобразований, имеем

Производная u′(δ) функции u(δ) в течение цикла работы механизма равна нулю при следующих значениях угла δ поворота дебалансов: δ₁=0°, δ₂=120°, δ₃=180°, δ₄=240° и δ₅=360°. Точки δ₁, δ₂, δ₃, δ₄, и δ₅ являются критическими точками функции u(δ). Определение знака производной в окрестностях критических точек свидетельствует о том, что функция u(δ) имеет следующие экстремумы: в точке δ₁ - максимум; в точке δ₂ - минимум; в точке δ₃ - максимум; в точке δ₄ - минимум; в точке δ₅ - максимум.

Вычислим экстремальные значения функции u(δ)=8cosδ+4cos2δ. Результаты вычислений представлены в таблице 3.

Таблица 3
δ, град	u(δ)=8cosδ+4cos2δ
0	12
120	-6
180	-4
240	-6

360

12

Степень несимметрии зависимости результирующего момента от угла поворота дебалансов составляет

На рисунке (фиг.8) представлен график зависимости результирующего момента сил инерции дебалансов в безразмерном выражении от угла поворота дебалансов за цикл работы механизма при .

Рассмотрим случай когда m₁=4m, m₂=m, r₁=r₂=r, l₁=4l, l₂=l. Тогда момент сил инерции первой пары дебалансов равен

Момент сил инерции второй пары дебалансов

Как видно из уравнений (24) и (25) максимальное значение момента сил инерции первой пары дебалансов в четыре раза больше максимального значения момента второй пары дебалансов, то есть

Результирующий момент в безразмерном выражении запишем в виде

Исследуем функцию u(δ)=16cosδ+4cos2δ на экстремумы. Производная функции имеет вид

После приравнивания производной нулю и преобразований, имеем

Производная u′(δ) функции u(δ) в течение цикла работы механизма равна нулю при следующих значениях угла δ поворота дебалансов: δ₁=0°, δ₂=180° и δ₃=360°. Точки δ₁, δ₂ и δ₃ являются критическими точками функции u(δ). Определение знака производной в окрестностях критических точек свидетельствует о том, что функция u(δ) имеет следующие экстремумы: δ₁ в точке - максимум; в точке δ₂ - минимум; в точке δ₃ - максимум.

Вычислим экстремальные значения функции u(δ)=16cosδ+4cos2δ. Результаты вычислений представлены в таблице 4.

Таблица 4
δ, град	u(δ)=16cosδ+4cos2δ
0	20
180	-12
360	20

Степень несимметрии зависимости результирующего момента от угла поворота дебалансов составляет

На рисунке (фиг.9) представлен график зависимости результирующего момента от сил инерции дебалансов в безразмерном выражении от угла поворота дебалансов за цикл работы механизма при .

Следует заметить, что, как видно из рисунка 9, при зависимость результирующего момента от угла поворота дебалансов в течение кинематического цикла вибровозбудителя имеет два экстремума.

На рисунке (фиг.10) показана зависимость степени несимметрии результирующего момента от соотношения максимальных моментов первой и второй пар дебалансов. Как видно из рисунка, наибольшую степень несимметрии зависимость результирующего момента имеет при отношении величины максимального момента, создаваемого силами инерции медленновращающихся дебалансов, к величине максимального момента, создаваемого силами инерции быстровращающихся дебалансов, равном двум, то есть равном передаточному отношению передачи, синхронизирующей и согласовывающей по фазе вращение дебалансов.

В рассмотренном случае, в соответствии с принятыми условиями, а именно в начальном положении, силы инерции медленно- и быстровращающихся дебалансов создают максимальные моменты одинакового направления и частота вращения одной пары дебалансов отличается от частоты вращения другой пары дебалансов в два раза, зависимость результирующего момента в безразмерном выражении в общем случае имеет вид

где a и b - коэффициенты, зависящие от отношения максимального момента сил инерции медленновращающихся дебалансов к максимальному моменту сил инерции быстровращающихся дебалансов.

Из уравнения (30) следует, что силы инерции медленновращающихся дебалансов создают максимальный момент положительного направления при cosδ=1 и максимальный момент в отрицательном направлении при cosδ=-1. Первое условие выполняется при δ=0° и δ=360°, а второе условие - при δ=180°. Аналогично рассуждая, приходим к выводу: силы инерции быстровращающихся дебалансов создают максимальный момент положительного направления при δ=0°, δ=180° и δ=360°, а максимальный момент отрицательного направления при δ=90° и δ=270°.

Из уравнения (30) следует, что силы инерции медленно- и быстровращающихся дебалансов создают моменты равные нулю соответственно при δ=90° и 270° и при δ=45°, 135°, 225° и 315°.

Из представленных рассуждений следует, что в рассмотренном случае силы инерции медленно- и быстровращающихся дебалансов одновременно создают максимальные моменты одинакового (положительного) направления только в одном положении дебалансов. Таким положением дебалансов является их начальное положение. При δ=180° силы инерции медл