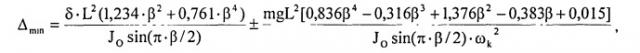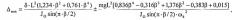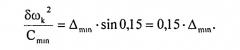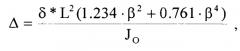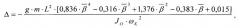Способ монтажа ротора газотурбинного двигателя

Способ монтажа ротора газотурбинного двигателя

Иллюстрации

Показать все

Реферат

Изобретение относится к роторным газотурбинным машинам и может быть использовано при монтаже их роторов, который осуществляется таким образом, что позволяет устранить резонанс роторов на критических частотах вращения, в том числе у высокооборотных газотурбинных двигателей, у которых критические частоты вращения роторов находятся в рабочем диапазоне частот.

Из уровня техники известно, что одной из основных проблем надежной работы газотурбинных машин является устранение резонанса их роторов на критических частотах вращения, когда силы, приводящие к прогибу вала ротора (центробежные силы от неуравновешенной массы ротора и гироскопические моменты роторных дисков), становятся равными силам упругого сопротивления вала и его поперечные перемещения при изгибе вала значительно возрастают.

Известные способы изменения критических частот вращения роторов по изгибной форме колебаний, при которых они теряют устойчивость (резонанс) за счет изменения конструкции: массовых, геометрических характеристик и жесткостей валов (см. Биргер И.А. Расчет на прочность деталей машин / Биргер И.А., Шорр Б.Ф., Иосилевич Г.Б. - М.: Машиностроение, 1979, 431 с.), часто затруднительны в реализации. Это связано с отсутствием возможности проводить конструктивные изменения на существующих двигателях, а также из-за того, что для высокооборотных двигателей невозможно избежать нахождения критических частот вращения в рабочем диапазоне их эксплуатации.

Известен способ безопасного разгона массивного ротора турбомашины, смонтированного в активных магнитных подшипниках, включающий быстрый переход ротора через критические частоты оборотов первых двух мод ротора (мод, соответствующих ротору как жесткому телу), причем у активных магнитных подшипников создают два режима: первый с возможно большей жесткостью, которую обеспечивают ресурсы управления с учетом отработки динамических воздействий в условиях длительной безопасной работы машины, и второй - с жесткостью, на один - четыре порядка, меньшей жесткости первого режима, причем разгон ротора начинают с первого режима, затем, по мере набора оборотов ротором, осуществляют согласно программе плавные (безударные) переключения с первого режима на второй и наоборот таким образом, что при разгоне полностью исключается работа ротора на резонансе и в резонансной области любой из мод в зоне от нуля до рабочих оборотов и при этом на всех режимах выполняется условие η<η_д, где η - перегрузка, η_д - допустимая перегрузка, а первое переключение осуществляют из дорезонансной зоны первой изгибной моды ротора первого режима в зарезонансную зону первой изгибной моды ротора второго режима (см. патент РФ №2265727, кл. F01D 19/00, 2005 г.).

В результате анализа известного решения необходимо отметить, что данный способ применим при отстройке от критических частот вращения роторов при разгоне двигателя, где, как правило, имеются резонансы, связанные со скалочной формой колебаний ротора, при которых вал не прогибается, а колебания происходят за счет упругости опоры и она сильно влияет на критические частоты. На больших частотах вращения характерны резонансы по изгибной форме колебаний ротора. Отстройка от резонанса при наличии критических частот вращения, находящихся в рабочем диапазоне, крайне сложна и не может быть осуществлена только с помощью изменения жесткости опоры, которая мало эффективна для изгибной формы колебаний. Кроме этого, магнитные подшипники представляют сложную конструкцию и не применимы для средних и тяжелых роторов авиационных двигателей, так как для их монтажа требуются громоздкие магнитные системы, а эксплуатация связана с большими затратами электрической энергии.

Известен способ устранения резонанса ротора при критической частоте его вращения, согласно которому вал ротора монтируют в подшипниках с овальными кольцами. В данном случае при вращении ротора круговое перемещение вектора центробежной силы от его неуравновешенной массы передается на опоры и в зонах кольца подшипника одной из опор с овальной дорожкой качения, где радиус-вектор его контура изменяется в направлении действия силы и это приращение превышает радиальное перемещение вала ротора на опоре, приводит к тому, что реакция опоры будет отсутствовать.

При полном отсутствии реакции опоры за время, равное четверти периода собственных колебаний ротора, приведет к тому, что прогиб вала устранится, и это явление будет предотвращать потерю устойчивости ротора при критической частоте вращения.

Устранение прогиба вала при овальной дорожке качения, расположенной на внешнем кольце подшипника, будет происходить в двух четвертях оборота вала, где радиус-вектор контура кольца возрастает (1 и 3 квадранты Фиг.1).

В двух других четвертях (2 и 4 квадранты Фиг. 1) реакция опоры восстановится, и в этот период ротор будет находиться в режиме, который подвержен потери устойчивости, но так как этот процесс будет чрезвычайно кратковременным, потери устойчивости ротора не будет.

Это подтверждает тот факт, что при пребывании на критических оборотах роторов на проходных режимах в течение времени, большего чем четверть оборота, потери устойчивости роторов не происходит. Достаточно, чтобы было обеспечено устранение прогиба вала в одной четверти оборота.

Собственная частота колебаний вращающего ротора на двух опорах будет ниже критической частоты вращения. В этом случае посадка вала ротора на опору и возникновение реакции на ней будет в т.Е (Фиг.1) и угол посадки ротора может определяться из условия

где β - параметр, определяющий посадку вала ротора в т.Е, при условии полного устранения прогиба вала, β=fк/fс; f_К - критическая частота вращения ротора, при которой он теряет устойчивость; fс - собственная частота колебаний ротора на двух опорах; ω_К - круговая скорость вращения ротора на критической частоте его вращения.

Минимальное значение овала при посадке вала ротора на опору, когда вал ротора полностью распрямится, определяется при t=βT/4 из выражения (начало отсчета в т. A)

где Δ_min - параметр овала, Δ_min=(D_max-D_min)/2; δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения

m_i и x_i - масса и координата диска относительно опоры с круговыми дорожками качения;

J_O - суммарный момент инерции ротора при его вращении относительно опоры, с круговыми дорожками качения, J O = ∑ i = 1 i = n m i x i 2 ; ω_k - круговая скорость вращения ротора; β - коэффициент, равный β=f_К/f_С; f_К и f_С - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора.

Здесь знак минус принимается при вращении вектора центробежной силы в первом квадранте, а знак плюс - в третьем.

Устранение реакции опоры при минимальном значении параметра овала Δ_min, обеспечивающего распрямление вала за время, равное четверти периода собственных колебаний ротора, способствует устранению резонанса при критической частоте вращения ротора. Максимальное значение параметра овала Δ_max принимается при посадке вала ротора за время, большее четверти периода собственной частоты колебания ротора при значении параметра β, равного 1,4 (См. Ю.Б. Назаренко. Устранение резонанса на критической частоте вращения роторов при эллиптической траектории вращения оси вала на опоре // Авиационно-космическая техника и технология. - Харьков: ХАИ. - 2013. №10(107). - С.60-65) - наиболее близкий аналог.

В результате анализа известного способа необходимо отметить, что монтаж ротора в подшипниках с овальными дорожками качения колец обеспечивает устранение резонанса ротора при критической частоте его вращения только на абсолютно жестких опорах, что не соответствует реальным условиям работы роторов при жесткостях опор, равных C=10⁶÷10¹⁰ Н/м.

Техническим результатом настоящего изобретения является повышение эффективности работы ротора за счет устранения резонанса ротора на критических частотах его вращения с помощью овализации беговой дорожки наружного кольца, параметры которой определяются с учетом податливости опоры ротора.

Сущность способа заключается в следующем. При монтаже ротора в одной из его опор используют подшипник роликовый с овальной беговой дорожкой кольца подшипника, связанного силовыми элементами со статором двигателя. Причем установку подшипника на опоре осуществляют таким образом, что большая ось овала кольца беговой дорожки совпадает с направлением силы тяжести ротора. Повышение устойчивости ротора на критической частоте его вращения происходит за счет устранения критических прогибов вала ротора. При угловом перемещении вектора центробежной силы от неуравновешенной массы ротора в зонах кольца подшипника, где приращение контура беговой дорожки совпадает с радиальным перемещением вала ротора на опоре и превышает его, реакция на вал со стороны опоры будет отсутствовать. Если реакция опоры будет отсутствовать в течение времени, равного четверти периода собственных колебаний ротора, вал распрямится.

Сущность заявленного способа поясняется чертежами, на которых:

- на фиг.1 - контур овальной дорожки качения кольца подшипника;

- на фиг.2 - ротор с установленными на нем дисками.

Указанный технический результат достигается тем, что параметры овала обеспечивают устранение прогиба вала в первой четверти оборота при посадке во второй четверти, так как в этом случае параметр овала будет минимальным и работа ротора будет стабильной. При этом устанавливают параметры овала, обеспечивающие устранение реакции на опоре в течение четверти периода свободных колебаний ротора с учетом податливости опоры.

Установление параметров овала, обеспечивающих устранение прогиба вала в течение четверти периода свободных колебаний ротора, произведенное с учетом податливости опоры, имеет ряд ограничений, выполнение которых позволит гарантированно обеспечить надежную реализацию данного технического решения.

При превышении собственного веса ротора его центробежной силы от неуравновешенной массы ротора на опоре посадки вала ротора на опоре во втором квадранте может вообще не быть. Принимаем, что центробежная сила на опоре должна в 1.1 раза превышать собственный вес ротора. Это условие реализуется при частоте вращения ротора ω K ≥ 1,1 ⋅ g m / δ .

Для упругих опор с определенной податливостью (обратная величина жесткости) в т.A под действием центробежной силы от неуравновешенной массы ротора происходит упругое смещение опоры. При круговом вращении ротора и его центробежной силы от т. A за отрезок времени Δt точка контакта вала выходит на контур несмещенного кольца и реакция опоры устраняется (Фиг.1).

Определим минимальное значение жесткости опоры для эффективной и надежной реализации способа на упругих опорах. Упругое смещение опоры на малой оси овала определится как отношение центробежной силы ротора на опоре δ ω K 2 от его дисбаланса δ к жесткости опоры C

Уравнение контура кольца овальной формы опишем тригонометрической функцией (Фиг.1)

R=R_O+Δsin(ω_kt),

где R_O - радиус кольца подшипника по малой оси овала; Δ - амплитуда (максимальное значение) отклонения контура кольца на большой оси овала относительно малой оси; ω_К - круговая скорость вращения ротора на критической частоте.

Представляя отклонение овального контура дорожки качения внешнего кольца от радиуса на меньшей оси овала в виде Δ_minsin(ω_kt), с учетом малого значения ω_kΔt, раскладывая в ряд Тейлора, получаем sin(ω_kt)=ω_kt.

Для выполнения условия малости аргумента при устранении реакции на опоре и условия, когда не будет преодолен предельный угол посадки вала ротора на опору, принимаем ω_kΔt=0.15 и приравняем упругое вдавливание вала на малой оси к отклонению контура овала в этой точке

Из последнего выражения получаем минимальное значение жесткости опоры для выполнения условия малости аргумента при выходе вала ротора на контур недеформируемой опоры

где µ_min - минимальное значение параметра овала, µ_min=2Δ_min=(D_max-D_min).

Определим параметры овала с учетом податливости опоры. Центробежная сила в т. A компенсируется реакцией опоры. При круговом движении центробежной силы вал ротора через интервал времени Δt выходит на контур недеформируемой опоры, реакция опоры пропадает и вал находится под действием только центробежной силы.

С этого момента начинает нарастать радиальное перемещение вала на опоре с овальной дорожкой качения. Радиальные перемещения от центробежной силы на податливой опоре будут такими же, как и для абсолютно жесткой опоры, только при увеличении времени до посадки вала ротора на опору на величину Δt.

Посадка вала ротора, определяющего минимальный параметр овала, будет происходить при значении параметра β, увеличенного на β', определяемого из условия α=0.15=β'·π/2

Перемещение вала ротора от статического и динамического дисбаланса на упругой опоре будет равно

где δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; J_O - суммарный момент инерции ротора при его вращении относительно опоры с круговыми дорожками качения, J O = ∑ i = 1 i = n m i x i 2 ; ω_k - круговая критическая скорость вращения ротора; β - коэффициент, равный, β=f_K/f_C; f_K и f_C - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора.

Перемещением вала ротора от его собственного веса определим за время, определяемое с момента устранения реакции и до посадки вала ротора на опору. Однако данное перемещение с достаточной точностью можно определить в интервале времени от t₁=0 до t 2 = T β ¯ / 4 , и оно составит

где β ¯ - коэффициент равный β ¯ = β + 0.095 .

Скорость, которую приобрел ротор в момент устранения реакции, оказывает существенное влияние на радиальные перемещения при посадке вала ротора на опору.

Скорость вала ротора, которую он получит на опоре за время Δt=0.15/ω_k от центробежных сил статического дисбаланса, будет равна

где Δt - время, за которое вал ротора выходит на контур несмещенного кольца и реакция опоры устраняется; ε - угловое ускорение ротора при его перемещении относительно опоры с круговой дорожкой качения, ε = δ ⋅ ω k 2 ⋅ L / J O ; δ - дисбаланс ротора на опоре, с овальной дорожкой качения; J_O - суммарный момент инерции ротора при его угловом перемещении относительно опоры с круговой дорожкой качения (См. Ю.Б. Назаренко. Поведение роторов на критических частотах вращения при овализации дорожки качения роликового подшипника // Двигатель, №6, 2012. - С.23).

Перемещение вала ротора на опоре, которое определим с момента устранения реакции на упругой опоре до момента его посадки от скорости, которую он получил за время Δt, составит

Минимальное значение параметра овала, определенное с учетом центробежных сил, собственного веса и с учетом перемещения от скорости, полученной в момент устранения реакции, составит

где Δ_min - параметр овала, Δ_min=(D_max-D_min)/2;

Минимальное значение параметра овала µ, равное разности максимального D_max и минимального D_min диаметра, определим при значениях β=1, β=1.1, β=1.2 и β=1.3

где λ - параметр, определяемый из выражения, λ=1.234·β²+0.761·β⁴+0.118β и равный 4.226, 5.474, 6.993 и 8.825 при β=1, β=1.1, β=1.2 и β=1.3; η - параметр, определяемый из выражения, η = 0,836 ⋅ β ¯ 4 − 0,316 ⋅ β ¯ 3 + 1,376 ⋅ β ¯ 2 − 0,383 ⋅ β ¯ + 0,015 и равный 4.065, 5.376, 6.983 и 8.933 при β=1, β=1.1, β=1.2 и β=1.3.

При определении минимального значения параметра овала возможна линейная экстраполяция между параметрами, определенными при β=1 и β=1.1, β=1.1 и β=1.2, а также β=1.2 и β=1.3.

Максимальное значение параметра овала Δ_max определяется при параметре β=1.35 и β ¯ = 1 .35 + 0 .095 = 1 .445

Статический дисбаланс ротора на опоре с овальной дорожкой качения определяется на балансировочной установке с технологическим подшипником с круговыми кольцами при диаметре беговой дорожки наружного кольца, равном минимальному диаметру овальной дорожки качения.

Область применения данного подшипника, используемого для устранения резонанса при критической частоте его вращения, определяется условием непревышения критической частоты вращения ротора на 30% собственной частоты колебаний ротора f_кр/f_с<1,3.

Заявленный способ будет более понятен из приведенного ниже примера. Пример реализован на роторе с тремя дисками из стали (Фиг.2), два из которых расположены на удалении от опор на расстоянии L/4 и один - посередине вала. Длина стального вала составляет L=0,5 м, внешний и внутренний диаметры вала равны 80 мм и 60 мм. Массы каждого диска (m₁, m₂, m₃) одинаковы и равны 10,2 кг, диаметр D=300 мм, и толщина t=20 мм. Дисбаланс ротора, приходящийся на опору с овальной дорожкой качения, равен δ=10 г*см.

Для принятых исходных данных собственная частота колебаний вала с дисками на двух опорах составила f_C=291,4 Гц, а критическая частота вращения вала 315,6 Гц (См. Ю.Б. Назаренко, А.Ю. Потапов. Способ устранения резонанса ротора турбореактивного двигателя при критической частоте его вращения с помощью овализации дорожки качения неподвижного кольца роликового подшипника // Двигатель. №1, 2012. - С.17).

Для устранения резонанса при критической скорости вращения ротора ω_k=1983 рад/с при параметре β=1.08 минимальное значение параметра овала на упругой опоре будет равно µ_min=8 мкм. Максимальное значение параметра овала на податливой опоре будет равно µ_max=18 мкм.

Условие превышения минимально допустимой жесткости опоры выполняется при жесткости опоры C>C_min=6.5*10⁸ Н/м. Минимально допустимая критическая скорость вращения составляет ω_К=1454 рад/с, что меньше фактической критической скорости вращения ω_k=1983 рад/с.

Аналогичная картина будет иметь место при овальной дорожке качения неподвижного внутреннего кольца, которое устанавливается на опору. При угловом перемещении вектора центробежной силы от неуравновешенной массы ротора в зонах кольца подшипника на участках с уменьшением радиуса дорожки качения внутреннего кольца и при приращении смещения контура к оси вращения, превышающем радиальное перемещение вала ротора на опоре в этом же направлении, реакция на вал со стороны опоры будет отсутствовать. В течение времени, равного четверти периода собственных колебаний ротора, вал ротора распрямится. Если, например, вектор центробежной силы от неуравновешенной массы ротора направлен на второй квадрант (Фиг.1), то посадка вала ротора на внутреннее кольцо будет осуществляться в первом квадранте. В этом случае силы тяжести будут уменьшать радиальное перемещение ротора и параметры овала будут такими же, как и для неподвижного наружного кольца при посадке вала ротора во втором квадранте.

Применение данного способа позволяет гарантированно обеспечить полное распрямление вала в одном из квадрантов за четверть периода собственных колебаний ротора и предотвратить резонанс ротора при критической частоте его вращения.

Способ монтажа ротора газотурбинного двигателя, согласно которому его устанавливают в подшипниковых опорах качения, отличающийся тем, что при монтаже ротора в одной из его опор используют подшипник роликовый с овальной беговой дорожкой кольца подшипника, связанного силовыми элементами со статором двигателя, причем установку подшипника на опоре осуществляют таким образом, что большая ось овала беговой дорожки кольца совпадает с направлением силы тяжести ротора, жесткость опоры выбирают из условия C > 13,3 ⋅ δ ω k 2 / μ min , параметр овала µ задают в диапазоне от минимального значения μ min = L 2 ( λ ⋅ δ − η ⋅ m ⋅ g / ω K 2 ) / [ sin ( π ⋅ β ¯ / 2 ) ⋅ J O ] и до максимального значения μ max = L 2 ( 12,896 ⋅ δ − 13,132 ⋅ m ⋅ g / ω K 2 ) / J O , где δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; J_O - момент инерции ротора при его угловом перемещении относительно опоры с круговыми дорожками качения подшипника; λ - параметр, равный λ=1,234·β²+0,761·β⁴+0,118β; η - параметр, равный η = 0,836 ⋅ β ¯ 4 − 0,316 ⋅ β ¯ 3 + 1,376 ⋅ β ¯ 2 − 0,383 ⋅ β ¯ + 0,015 ; β - коэффициент, равный β=f_К/f_С; β ¯ - коэффициент, равный β ¯ = β + 0,095 ; f_К и f_С - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора; L - пролет ротора; C - жесткость опоры; µ - параметр овала дорожки качения кольца подшипника, µ=(D_max-D_min); D_max и D_min - максимальный и минимальный диаметр овальной дорожки качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; g - ускорение свободного падения.