Градиентная линза с апланатическими и телескопическими свойствами

Градиентная линза с апланатическими и телескопическими свойствами

Иллюстрации

Показать все

Реферат

1. Область техники, к которой относится изобретение

Предлагаемое изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении для создания объективов, конденсоров, эндоскопов, устройств согласования волоконно-оптических линий связи с источниками излучения и фотоприемниками и т.д.

2. Уровень техники

Известна апланатическая градиентная линза [1], ограниченная первой и второй преломляющими поверхностями вращения, имеющая по оптической оси z толщину d, кратную удвоенному номинальному фокусному расстоянию, выполненная из материала с радиальным распределением показателя преломления n(y), определяемым из уравнения

n ( y ) = n 0 sec h a y = 2 n 0 e a y + e - a y ,   ( 1 )

где n₀ - значение показателя преломления на оси;

а - постоянная;

имеющая образующую y₁(z) первой выпуклой поверхности, определяемую уравнением

y 1 2 ( z ) = ( n 2 ( y ) − 1 ) z 2 + 2 s F ( n ( y ) − 1 ) z ,   ( 2 )

где s_F - передний отрезок;

и имеющая образующую y₂(z) второй вогнутой поверхности, определяемую уравнением

y 2 2 ( z ) = ( n 2 ( y ) − 1 ) ( z − d ) 2 + 2 s ' F ' ( n ( y ) − 1 ) ( z − d ) ,   ( 3 )

где s F ' ' - задний отрезок;

причем s F ' ' = s F .

Заметим, величины s_F и s F ' ' , положительны и указаны здесь и далее без применения правил знаков для отрезков, принятых в геометрической оптике [2].

Форма обеих преломляющих поверхностей в известной линзе одинакова. Образующие (2) и (3) могут быть условно названы гиперболами высшего порядка.

Известно, что длина периодичности L для распределения показателя преломления (ПП), определяемого уравнением (1) и называемого также гиперсекансным, равна [2]

L = 2 π a ,

соответственно, половина длины периодичности

L 2 = π a

Номинальное фокусное расстояние линзы с гиперсекансным распределением ПП

f 0 ' = L 4 = π 2 a ,

удвоенное номинальное фокусное расстояние будет равно половине длины периодичности

F = 2 f 0 ' = L 2 = π a   ( 4 )

При выборе определенной толщины линзы с распределением ПП вида (1) и плоскими 1-й и 2-й поверхностями, перпендикулярными оптической оси, может быть получена фокусирующая, рассеивающая или телескопическая линза [2]. При этом вполне очевидно, что телескопическая линза получается в случае выбора толщины линзы, равной удвоенному номинальному фокусному расстоянию, в результате чего входной параллельный пучок лучей, также параллельный оптической оси, на выходе линзы останется параллельным.

Известно также уравнение траектории хода луча в среде с распределением ПП (1), так, если начальная высота точки, из которой начинает распространяться луч, равна b_T, начальная координата z_T и начальный коэффициент наклона (тангенс начального угла наклона луча) φ₁, то уравнение траектории хода луча принимает следующий вид [3]

y Л ( z ) = 1 a a r s h ( s h a b T cos a ( z − z T ) + ϕ 1 c h a b T sin a ( z − z T ) )   ( 5 )

Соответственно, учитывая, что

a r s h x = ln ( x + x 2 + 1 )

и

[ a r s h x ] ' = 1 x 2 + 1

можно записать

x = s h a b T cos a ( z − z T ) + ϕ 1 c h a b T sin a ( z − z T ) ,   ( 6 )

y Л ( z ) = 1 a ln ( x + x 2 + 1 ) ,   ( 7 )

а производная определяется из выражения

y ' Л ( z ) = ϕ 1 c h a b T cos a ( z − z T ) − s h a b T sin a ( z − z T ) [ s h a b T cos a ( z − z T ) + ϕ 1 c h a b T sin a ( z − z T ) ] 2 + 1   ( 8 )

Отметим, что, если длина отрезка между координатами точки выхода луча из линзы z_ВЫХ и точки входа луча в линзу z_ВХ

d=z_ВЫХ-z_ВХ

равна длине периодичности

L = 2 π a ,

то высота точки выхода луча из линзы y_ВЫХ, согласно (5), будет равна высоте точки входа луча в линзу y_ВХ, или

y В Ы Х = y В Х   ( 9 )

В результате, значение ПП в точке входа луча в линзу будет равно значению ПП в точке выхода луча из линзы

n ( y В Ы Х ) = n ( y В Х ) ,   ( 10 )

При этом, согласно (8), тангенс угла наклона луча φ₂, попадающего в точку выхода луча из линзы перед преломлением, будет равен начальному тангенсу угла наклона φ₁

ϕ 2 = ϕ 1   ( 11 )

а значение производной будет соответствовать исходному

y ' Л ( z В Х ) = y ' Л ( z В Ы Х ) ,   ( 12 )

Если же длина отрезка d между координатами точки выхода луча из линзы z_ВЫХ и точки входа луча в линзу z_ВХ равна половине длины периодичности

L 2 = π a

то высота точки выхода луча из линзы y_ВЫХ, согласно (5), будет равна высоте точки входа луча в линзу y_ВЫХ, взятой с обратным знаком

y В Ы Х = − y В Х ,   ( 13 )

значение ПП в точке входа луча в линзу будет равно значению ПП в точке выхода луча из линзы

n(y_ВЫX)=n(y_ВX),

тангенс угла наклона луча φ₂, попадающего в точку выхода луча из линзы перед преломлением, будет равен начальному тангенсу угла наклона φ₁, взятому с обратным знаком

ϕ 2 = − ϕ 1   ( 14 )

а значение производной будет равно по абсолютной величине исходному, но взятому с обратным знаком

y ' Л ( z В Х ) = − y ' Л ( z В Ы Х ) ,   ( 15 )

В известной линзе, согласно замыслу, каждый луч гомоцентрического пучка излучения, выходящий из точки на оптической оси, после преломления на первой поверхности приобретает направление, параллельное оптической оси. Затем, распространяясь внутри линзы в градиентной среде по криволинейной симметричной траектории, каждый луч достигает второй преломляющей поверхности. В точке пересечения со второй преломляющей поверхностью луч имеет направление, также параллельное оптической оси.

После преломления на второй поверхности каждый луч приобретает исходное направление, позволяющее вновь образовать гомоцентрический расходящийся пучок, центр которого также располагается на оптической оси на расстоянии s F ' ' = s F от центра второй поверхности. При этом s F ' ' является задним отрезком линзы (фиг.1).

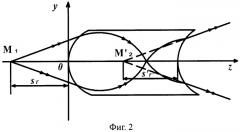
В зависимости от выбираемой толщины линзы d, кратной удвоенному номинальному фокусному расстоянию, преломление на второй поверхности может происходить как выше оптической оси, так и ниже оси (если условно считать начальное преломление на первой поверхности происходящим выше оптической оси), что, однако, не влияет на способность линзы формировать на выходе гомоцентрический расходящийся пучок (фиг.2).

Известная линза выбирается за прототип предполагаемого изобретения.

Известная линза позволяет формировать на выходе расходящийся гомоцентрический пучок излучения только с помощью двух преломляющих поверхностей вращения одинаковой формы, имеющих образующую функцию довольно сложного вида, что усложняет ее изготовление.

Таким образом, невозможность применения в качестве преломляющих поверхностей других поверхностей, в том числе более простой формы, является недостатком известной линзы, ограничивающим возможности ее изготовления.

Кроме того, известная линза является апланатической, но наличие у нее одновременно и телескопических свойств неизвестно.

3. Раскрытие изобретения

Предлагаемое техническое решение призвано устранить указанный недостаток известной линзы.

Техническим результатом, достигаемым при использовании предполагаемого изобретения, является

1) расширение возможностей изготовления за счет возможности выбора разных форм преломляющих поверхностей,

2) упрощение конструкции линзы за счет возможности выбора более простой формы преломляющих поверхностей;

3) расширение функциональных возможностей линзы за счет наличия, наряду с апланатическими, также одновременно телескопических свойств.

Для достижения указанного технического результата предлагается градиентная линза,

ограниченная первой и второй преломляющими поверхностями,

выполненная из материала с радиальным распределением показателя преломления n(y), определяемым из уравнения

n ( y ) = n 0 sec h a y = 2 n 0 e a y + e - a y ,

где n₀ - значение показателя преломления на оси;

а - постоянная;

имеющая по оптической оси z толщину d, кратную удвоенному номинальному фокусному расстоянию F, равному

F = π a ,

имеющая равные величины переднего s_F и заднего s F ' ' , отрезков.

причем при толщине, кратной F, проекция толщины линзы на оптическую ось в любой плоскости, содержащую оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по абсолютной величине высоту относительно оптической оси, но расположенных по разные стороны от оптической оси, равна F,

а при толщине, кратной 2F, проекция толщины линзы на оптическую ось в любой плоскости, содержащую оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по величине высоту относительно оптической оси и расположенных по одну сторону от оптической оси, равна 2F.

В отдельных случаях выполнения в предлагаемой линзе 1-я и 2-я преломляющие поверхности являются поверхностями вращения одинаковой формы, в частности, сферическими.

Кроме этого, в предлагаемой линзе образующие 1-й и 2-й преломляющих поверхностей могут быть прямыми, а сами поверхности представлять собой наклонные плоскости и, в частности, плоскости, перпендикулярные оптической оси линзы.

Помимо этого, в предлагаемой линзе 1-я и 2-я преломляющие поверхности могут быть образованы двумя пересекающимися плоскостями, причем образующие каждой плоскости являются прямыми с разными коэффициентами наклона.

Указанный технический результат можно достичь, если принять во внимание замечательное свойство исходной линзы, имеющей толщину кратную длине периодичности, сохранять на выходе исходное направление луча, попадающего на 1-ю поверхность, вне зависимости от выбранной формы для 1-й и 2-й поверхности, а также от величины переднего отрезка и. соответственно, положения источника излучения.

Линза, имеющей толщину, кратную половине длины периодичности, обладает сходным свойством - сохранять на выходе абсолютное значение коэффициента наклона входного луча, попадающего на 1-ю поверхность, вне зависимости от выбранной формы для 1-й и 2-й поверхности, а также от величины переднего отрезка и, соответственно, положения источника излучения, но при этом на выходе знак коэффициента наклона преломленного луча меняется на противоположный.

Покажем действие этих свойств сначала для линз с минимальной толщиной и выберем для рассмотрения линзы с толщиной, равной длине периодичности L и половине длины периодичности L/2.

Для линз с большей толщиной, кратной половине длины периодичности, действие этих свойств также сохраняется.

Линза толщиной d на оптической оси, равной длине периодичности L, выполнена из материала с радиальным распределением ПП n(y), соответствующим уравнению (1) и известным для заданной длины волны, ограничена 1-й и 2-й преломляющими поверхностями одинаковой формы с образующими y₁(z) и y₂(z) и расположена в однородной среде (примем ПП однородной среды n₁=1 (воздух)).

Одинаковая форма преломляющих поверхностей в рассматриваемом случае линзы с толщиной d, равной длине периодичности L, означает, что 2-я поверхность фактически представляет собой 1-ю поверхность после параллельного переноса вдоль оптической оси z на расстояние d.

В результате, расстояние вдоль оси z между любой отдельно взятой исходной точкой на 1-й поверхности, имеющей определенную высоту над осью z, и точкой на 2-й поверхности, имеющей такую же высоту над осью z и находящейся на одной прямой, параллельной оси z, с исходной точкой на 1-й поверхности, будет одинаковым и равным толщине d=L.

В самом простом случае, 1-я и 2-я преломляющие поверхности могут быть поверхностями вращения, но, в более общем случае, это необязательно.

Вершина 1-й поверхности расположена в начале координат. Ось z представляет собой оптическую ось линзы. Принимая, что линза обладает осевой симметрией, рассмотрение проводится в меридиональной плоскости.

Луч падающего на 1-ю поверхность пучка, выходящего из точки М, на оптической оси, имеет направляющий коэффициент и u_K1=φ₁, преломляется в точке А с координатами z_П1, y_П1. Угол падения луча на 1-ю поверхность обозначим как ε₁, угол преломления на 1-й поверхности - ε 1 ' , нормаль к 1-й поверхности в точке А - N₁, угол падения луча на 2-ю поверхность - ε₂, угол преломления на 2-й поверхности - ε 2 ' , а нормаль ко 2-й поверхности в точке преломления В - N₂.

Направляющий коэффициент входного луча, преломляющегося на 1-й поверхности в точке А обозначим как и u_K1, направляющий коэффициент луча, преломленного на 1-й поверхности в точке А, - u_B1, направляющий коэффициент луча, преломляющегося на 2-й поверхности в точке В, - u_K2, направляющий коэффициент луча, преломленного на 2-й поверхности в точке В, - u_B2.

Направляющий коэффициент u_H1 нормали N₁ к 1-й поверхности в точке А можно выразить в виде

u H 1 = − 1 y 1 ' ( z ) ,   ( 16 )

где y 1 ' ( z ) - первая производная от y₁(z).

Направляющий коэффициент u_H2 нормали N₂ ко 2-й поверхности в точке В можно выразить в виде

u H 2 = − 1 y 2 ' ( z ) ,   ( 17 )

где y 2 ' ( z ) - первая производная от y₂(z).

Случай 1-й выпуклой поверхности для линзы с толщиной, кратной L

Рассмотрим случай 1-й выпуклой поверхности для линзы с толщиной, кратной L.

Случаи преломления на 1-й выпуклой и 2-й вогнутой поверхностях показаны на фиг.3 и 5.

Схемы преломления на фиг.3 и 5 относятся к случаям, когда после преломления направляющий коэффициент и g, преломленного на 1-й поверхности (выходного) луча имеет отрицательное значение (фиг.3) и положительное значение (фиг.5).

Соответственно, общая схема хода лучей в линзе показана для u_B1<0 на фиг.4, а для u_B1>0 - на фиг.6.

Для обеих возможных схем преломления, представленных на фиг.3 и 5, в точке А на 1-й поверхности угол падения ε₁ можно определить из выражения

t g ε 1 = u K 1 − u H 1 1 + u K 1 u H 1 ,   ( 18 )

а угол преломления ε 1 ' - из выражения

t g ε ' 1 = u B 1 − u H 1 1 + u B 1 u H 1 ,   ( 19 )

Кроме того, по закону преломления,

n 1 sin ε 1 = n ( y П 1 ) sin ε 1 ' ,

где n(y_П1) - ПП в точке преломления А.

Тогда, с учетом того, что n₁=1, угол преломления выразится в виде

sin ε 1 ' = sin ε 1 n ( y П 1 ) ,   ( 20 )

Поскольку преломленный в точке А на 1-й поверхности луч. имея начальное направление u_B1, после преломления распространяется по криволинейной траектории с периодом, равным длине периодичности L, то в точке В, после прохождения полного периода,

1) высота y_П2 точки преломления В будет равна высоте y_П1 точки преломления А, согласно условию (9);

2) направляющий коэффициент u_K2=φ₂ падающего на 2-ю поверхность луча будет равен u_B1=φ₁, согласно условию (11), и соответственно,

u K 2 = u B 1 ;   ( 21 )

3) направляющий коэффициент u_H2 нормали N₂ ко 2-й поверхности в точке В будет равен направляющему коэффициенту u_H1 нормали N₁ к 1-й поверхности в точке А, по условию (11) и соотношениям (12), (16) и (17), поскольку форма 1-й и 2-й поверхностей одинакова, и, таким образом,

u H 2 = u H 1   ( 22 )

Угол падения ε₂ в точке В будет равен

t g ε 2 = u K 2 − u H 2 1 + u K 2 u H 2 ,   ( 23 )

Учитывая (21) и (22) и подставляя в (23), получим

t g ε 2 = u B 1 − u H 1 1 + u B 1 u H 1 ,   ( 24 )

Сравнивая (19) и (24), получаем, что

ε 1 ' = ε 2

на основе чего можно также записать

sin ε 2 = sin ε 1 ' ,   ( 25 )

Для точки В на 2-й поверхности, по закону преломления

n ( y П 2 ) sin ε 2 = n 1 sin ε 2 ' ,

где n(y_П2) - ПП в точке преломления В.

С учетом того, что n₁=1, угол преломления выразится в виде

sin ε 2 ' = n ( y П 2 ) sin ε 2

Принимая во внимание соотношения (20) и (25), получим

sin ε 2 ' = n ( y П 2 ) sin ε 1 n ( y П 1 )

Поскольку в точке В, как указано выше, y_П2=y_П1, и, соответственно, согласно условию (10), выполняется соотношение n(y_П2)=n(y_П1), то получим, что

sin ε 2 ' = sin ε 1

и тогда, как следствие,

ε 2 ' = ε 1

и

t g ε 2 ' = t g ε 1   ( 26 )

Угол преломления ε 2 ' в точке В можно также выразить в виде

t g ε 2 ' = u B 2 − u H 2 1 + u B 2 u H 2

Если использовать в этом выражении соотношение (22), то получим

t g ε 2 ' = u B 2 − u H 1 1 + u B 2 u H 1 ,   ( 27 )

Приравняв, на основе (26), выражения (18) и (27) и проведя простые преобразования, получим

u_B2=u_K1

Таким образом, направление выходного луча, преломленного в точке В, будет совпадать с направлением входного луча в точке А.

Случай 1-й выпуклой поверхности для линзы толщиной L/2

Рассмотрим случай 1-й выпуклой поверхности для линзы с толщиной, кратной L/2.

Случаи преломления на 1-й выпуклой и 2-й вогнутой поверхностях показаны на фиг.7 и 9.

Схемы преломления, показанные на фиг.7 и 9, относятся к случаям, когда после преломления направляющий коэффициент u_B1 преломленного на 1-й поверхности луча имеет отрицательное значение (фиг.7) и положительное значение (фиг.9).

Соответственно, общая схема хода лучей в линзе показана для и u_B1<0 на фиг.8, а для u_B1>0 - на фиг.10.

Для обеих возможных схем преломления, представленных на фиг.7 и 9, в точке А на 1-й поверхности угол падения ε₁ можно определить из выражения

t g ε 1 = u K 1 − u H 1 1 + u K 1 u H 1 ,   ( 28 )

а угол преломления ε 1 ' - из выражения

t g ε 1 ' = u B 1 − u H 1 1 + u B 1 u H 1 ,   ( 29 )

Кроме того, по закону преломления,

n 1 sin ε 1 = n ( y П 1 ) sin ε 1 '

Тогда, с учетом того, что n₁=1, угол преломления выразится в виде

t g ε 1 ' = sin ε 1 n ( y П 1 ) ,   ( 30 )

Для линзы с длиной периодичности L/2 преломленный в точке А на 1-й поверхности луч, имея начальное направление u_B1, после преломления распространяется по периодической криволинейной траектории, и в точке В, после прохождения половины периода,

1) высота y_П2 точки преломления В будет равна по абсолютной величине высоте y_П1 точки преломления А, но будет иметь отрицательное значение, согласно условию (13);

2) направляющий коэффициент u_K2=φ₂ падающего на 2-ю поверхность луча будет равен u_B1=φ₁ по абсолютной величине, но будет иметь отрицательное значение, согласно условию (14), и, таким образом,

u K 2 = − u B 1 ;   ( 31 )

3) направляющий коэффициент u_H2 нормали N₂ к 1-й поверхности в точке В будет равен направляющему коэффициенту u_H1 нормали N₁ к 1-й поверхности в точке А по абсолютной величине, но будет иметь отрицательное значение, согласно условию (15)

u H 2 = − u H 1   ( 32 )

Угол падения ε₂ в точке В будет равен

t g ε 2 = u H 2 − u K 2 1 + u K 2 u H 2 ,   ( 33 )

Учитывая (31) и (32) и подставляя в (33), получим

t g ε 2 = u B 1 − u H 1 1 + u B 1 u H 1 ,   ( 34 )

Сравнивая (29) и (34), получаем, что

ε 1 ' = ε 2 ,

на основе чего можно также записать

sin ε 2 = sin ε 1 ' ,   ( 35 )

Для точки В на 2-й поверхности, по закону преломления

n ( y П 2 ) sin ε 2 = n 1 sin ε 2 ' ,

где n(y_П2) - ПП в точке преломления В.

Соответственно, с учетом того, что n₁=1, угол преломления выразится в виде

sin ε 2 ' = n ( y П 2 ) sin ε 2

Принимая во внимание соотношение (30) и (35), получим

sin ε 2 ' = n ( y П 2 ) sin ε 1 n ( y П 1 )

Поскольку в точке В, как указано выше, y_П2=-y_П1, но при этом n(y_П2)=n(-y_П1), то получим, что

sin ε 2 ' = sin ε 1

и тогда, как следствие,

ε 2 ' = ε 1 ,

и

t g ε 2 ' = t g ε 1   ( 36 )

Угол преломления ε 2 ' в точке В можно также выразить в виде

t g ε 2 ' = u H 2 − u B 2 1 + u B 2 u H 2