Способ определения односторонних логарифмических декрементов колебаний

Способ определения односторонних логарифмических декрементов колебаний

Иллюстрации

Показать все

Реферат

Изобретение относится к области экспериментальных исследований характеристик рассеивания энергии при колебаниях, а именно к способам определения односторонних логарифмических декрементов колебаний при резонансных испытаниях, и может быть использовано при исследовании динамических характеристик, прочности и устойчивости конструкций и материалов.

Известны несколько способов определения декрементов колебаний по резонансным кривым. Наиболее близким к предлагаемому способу является способ, принятый за прототип, патент RU №2086943, С1, МПК G01M 7/02, 1997 г., по которому гармонической силой постоянной амплитуды возбуждают колебания исследуемого объекта, регистрируют резонансные частоты f_p и амплитуды перемещений a _p=a(f_p) при резонансных частотах, затем путем изменения частоты f вынуждающей силы снижают амплитуду перемещений до выбранной величины a(f), фиксируют ее и соответствующую ей частоту колебаний f и по формуле:

δ a = π ⋅ z a | 1 − u 2 | | 1 − u 2 z a 2 | , где z a = a ( f ) a ( f p ) - степень спада, u = f f p ,

рассчитывают логарифмический декремент колебаний δ_a.

Все названные признаки, кроме регистрации амплитуды колебаний и расчета логарифмического декремента по вышеприведенной формуле, присутствуют в предлагаемом способе.

Ограниченностью принятого в качестве прототипа способа является невозможность использования для определения логарифмических декрементов колебаний резонансных кривых, основанных на разложении сигналов откликов на синфазную (действительную) и квадратурную (мнимую) составляющие, наиболее широко применяемые в современных системах частотных испытаний. Способ также ограничен в выборе датчиков первичной информации: для его реализации необходимо измерять амплитуду перемещений или пропорциональный ей параметр, например амплитуду относительных деформаций.

Изобретение направлено на создание способа определения односторонних логарифмических декрементов колебаний, свободного от упомянутых ограничений.

Это достигается благодаря тому, что в предлагаемом способе определения односторонних логарифмических декрементов колебаний гармонической силой постоянной амплитуды возбуждают колебания исследуемого объекта, регистрируют резонансные частоты f_p и кинематический параметр q_p=q(f_p) [амплитуды колебаний перемещений (q=a), скоростей (q=ν) или ускорений (q=n), или квадратурные составляющие частотных характеристик перемещений (q=I_a), ускорений (q=I_n), или синфазные составляющие частотных характеристик скоростей (q=R_ν)] при резонансных частотах, затем путем изменения частоты f вынуждающей силы снижают q(f) до выбранной величины фиксируют ее и соответствующую ей частоту колебаний f, по полученным экспериментальным значениям частот f и f_p и величин q(f) и q(f_p) рассчитывают логарифмические декременты колебаний по формулам (u=f/f_p):

δ a = π ⋅ z a | 1 − u 2 | | 1 − u 2 z a 2 | , z a = a ( f ) a ( f p ) , если q=a;

δ n = π z n | 1 − u 2 | u | u 2 − z n 2 | , z n = n ( f ) n ( f p ) , если q=n;

δ ν = π z ν | 1 − u 2 | u | 1 − z ν 2 | , z ν = ν ( f ) ν ( f p ) , если q=ν;

δ 1 a = π | 1 − u 2 | u | u z 1 a − u 2 | , z 1 a = I a ( f ) I a ( f p ) , если q=I_an;

δ 1 ν = π z 1 ν 1 − z 1 ν | 1 − u 2 | u , z 1 ν = R ν ( f ) R ν ( f p ) , если q=R_ν;

δ 1 n = π | 1 − u 2 | u | 1 − u z 1 π | , z 1 n = I n ( f ) I n ( f p ) , если q=I_n.

Отличительными признаками изобретения являются следующие: помимо перемещений измеряемыми величинами могут быть скорости, ускорения, квадратурные составляющие частотных характеристик перемещений и ускорений, синфазные составляющие частотных характеристик скоростей и логарифмические декременты колебаний рассчитывают (если измеряемыми величинами не являются перемещения) по формулам (u=f/f_p):

δ n = π z n | 1 − u 2 | u | u 2 − z n 2 | , z n = n ( f ) n ( f p ) , если q=n;

δ ν = π z ν | 1 − u 2 | u | 1 − z ν 2 | , z ν = ν ( f ) ν ( f p ) , если q=ν;

δ 1 a = π | 1 − u 2 | u | u z 1 a − u 2 | , z 1 a = I a ( f ) I a ( f p ) , если q=I_an;

δ 1 ν = π z 1 ν 1 − z 1 ν | 1 − u 2 | u , z 1 ν = R ν ( f ) R ν ( f p ) , если q=R_ν;

δ 1 n = π | 1 − u 2 | u | 1 − u z 1 π | , z 1 n = I n ( f ) I n ( f p ) , если q=I_n.

В результате поиска по источникам патентной и научно-технической информации решений, содержащих такой признак, не обнаружено.

Следовательно, можно сделать заключение о том, что предложенное решение неизвестно из уровня техники и соответствует критерию охраноспособности - «новое».

Способ может быть осуществлен на конструкциях, элементах конструкций, образцах материалов при изгибных, крутильных или продольных колебаниях, возбуждаемых силовым или кинематическим способом, и может найти применение в машиностроении, ветроэнергетике, строительстве и т.д., где требуется определить динамические характеристики (частоты, формы и логарифмические декременты колебаний) механических конструкций, при исследовании механических свойств материалов, что позволяет сделать вывод о соответствии критерию «промышленная применимость».

Рассмотрим, например, реализацию способа при изгибных колебаниях летательного аппарата с плотным спектром частот при силовом его возбуждении.

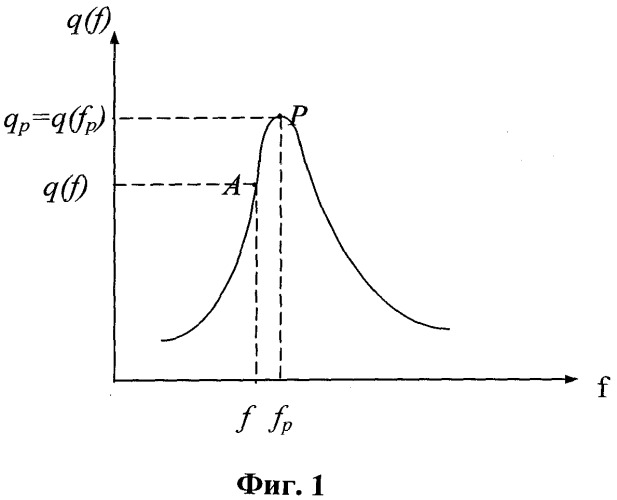
Испытуемый образец мягко подвешивают на резиновых амортизаторах так, чтобы частота его колебаний на амортизаторах не превышала 10% от низшей собственной частоты. В одном из сечений к испытуемому образцу жестко подсоединяют подвижную часть специального электродинамического вибратора и возбуждают колебания при постоянном значении амплитуды возбуждающей силы. Варьируют частоты вынуждающей силы и по изменению какого-либо кинематического параметра q(f), например квадратурной составляющей I_n(f) комплексной передаточной функции одного из акселерометров, установленных на испытуемом образце, определяют резонанс. Регистрируют резонансную частоту f_p колебаний и резонансное значение выбранного кинематического параметра q(f_p). Точка резонансного пика Р с частотой f_p и амплитудой q_p=q(f_p), соответствующая резонансу, представлена на фиг.1. Затем путем изменения частоты f вынуждающей силы снижают q(f) до выбранной величины (точка А), фиксируют ее и соответствующую ей частоту колебаний f.

По полученным экспериментальным данным вычисляют степень спада z=q(f)/q(f_p), после чего определяют по соответствующей формуле логарифмический декремент колебаний δ.

Данный способ реализован в лабораторных условиях. В качестве испытуемого образца использовался корпус летательного аппарата. В качестве кинематического параметра q(f) была принята квадратурная составляющая I_n(f) комплексной передаточной функции одного из акселерометров типа АС 565/1, установленных на корпусе. Возбуждение осуществлялось специальным электродинамическим вибратором 20JE20/C. Управление возбуждением, измерения и выделение синфазной и квадратурной составляющих частотных характеристик осуществлялось управляющей измерительно-вычислительной системой PRIN85, входящей в состав комплекса частотных испытаний PRODERA.

Результаты вычисления логарифмических декрементов по экспериментально полученным значениям f, f_p, I_n(f) и I_n(f_p) приведены в таблице. Там же приведены результаты вычисления логарифмических декрементов по формуле патента (RU №2086943, С1)

δ a = π ⋅ z a | 1 − u 2 | | 1 − u 2 z a 2 | , где z a = a ( f ) a ( f p ) .

Сравнение подтвердило близость полученных при осуществлении изобретения результатов.

Таблица
fp, Гц	f, Гц	δ1n	δa
21,4	21,2	0,05	0,06
	21,6	0,11	0,12
	21,7	0,11	0,13
41,6	38,6	0,54	0,52
	39,6	0,59	0,62
	41,1	0,53	0,49
74,2	76,4	0,33	0,37

Способ определения односторонних логарифмических декрементов колебаний, по которому гармонической силой постоянной амплитуды возбуждают колебания исследуемого объекта, регистрируют резонансные частоты f_p и кинематический параметр q_p=q(f_p): амплитуды колебаний перемещений (q=a), скоростей (q=ν) или ускорений (q=n), или квадратурные составляющие частотных характеристик перемещений (q=I_a), ускорений (q=I_n), или синфазные составляющие частотных характеристик скоростей (q=R_ν) при резонансных частотах, затем путем изменения частоты f вынуждающей силы снижают q(f) до выбранной величины, фиксируют ее и соответствующую ей частоту колебаний f, по полученным экспериментальным значениям частот f и f_p и величин q(f) и q(f_p) рассчитывают логарифмические декременты, отличающийся тем, что помимо перемещений измеряемыми величинами могут быть скорости, ускорения, квадратурные составляющие частотных характеристик перемещений и ускорений, синфазные составляющие частотных характеристик скоростей и логарифмические декременты колебаний рассчитывают (если измеряемыми величинами не являются перемещения) по формулам (u=f/f_p): , , если q=n; , , если q=ν; , , если q=I_a; , , если q=R_ν; , , если q=I_n..