Способ определения логарифмических декрементов колебаний по ширине резонанса равноинтенсивных колебаний

Способ определения логарифмических декрементов колебаний по ширине резонанса равноинтенсивных колебаний

Иллюстрации

Показать все

Реферат

Изобретение относится к области экспериментальных исследований характеристик рассеивания энергии при колебаниях, а именно к способам определения логарифмических декрементов колебаний по ширине резонанса равноинтенсивных колебаний (комплексным частотным характеристикам), и может быть использовано при исследованиях динамических характеристик, прочности и устойчивости конструкций и материалов.

С резонансным методом обычно [Г.М. Мякишев, Б.И. Рабинович «Динамика тонкостенных конструкций с отсеками, содержащими жидкость», М., «Машиностроение», 1971 г., разделы 10.2, 10.3, с.319…329] связывают определение логарифмических декрементов колебаний по ширине резонансного пика на уровне вынужденных колебаний с энергии, составляющей 50% энергии колебаний при резонансе. В этом случае испытуемую конструкцию возбуждают гармонической силой (или моментом) постоянной амплитуды, изменяют частоту вынуждающей силы, измеряют один из кинематических параметров колебаний испытуемого объекта (амплитуды перемещений, скоростей, ускорений или их комплексные отклики: квадратурные и синфазные составляющие откликов), строят по этому параметру резонансные кривые H(f),) (амплитудно-частотные характеристики или составляющие комплексных откликов), находят резонансные частоты f_p, как частоты, соответствующие максимумам резонансных кривых H(f), и характерные частоты f₂>f₁, как частоты, соответствующие точкам пересечения резонансных кривых с прямой, проведенной параллельно оси частот (оси абсцисс) на высоте, равной высоте резонансного пика Н_р=H(f_p), деленной на √2 (если строят амплитудные частотные характеристики) и на 2 (если строят квадратурные составляющие откликов по перемещению или ускорению или синфазные составляющие откликов по скорости). По величине характерных частот f₁ и f₂ находят ширину резонансного пика Δf=f₂-f₁ и по формуле логарифмический декремент колебаний. Все названные признаки, кроме определения ширины резонансных пиков на фиксированной высоте (1/√2)·Н_р (если строят амплитудные частотные характеристики) и (1/2)·Н_р (если строят квадратурные составляющие откликов по перемещению или ускорению или синфазные составляющие откликов по скорости) для расчетов логарифмических декрементов по приведенной формуле присутствуют в настоящем техническом решении.

Таким способом логарифмические декременты легко определяются, если резонансные пики хорошо выражены и достаточно далеко отстоят друг от друга. В противном случае определение логарифмических декрементов способом, принятым в качестве прототипа, затруднено, а порой и невозможно.

Изобретение направлено на создание способа определения логарифмических декрементов колебаний по резонансным кривым, свободного от упомянутых ограничений.

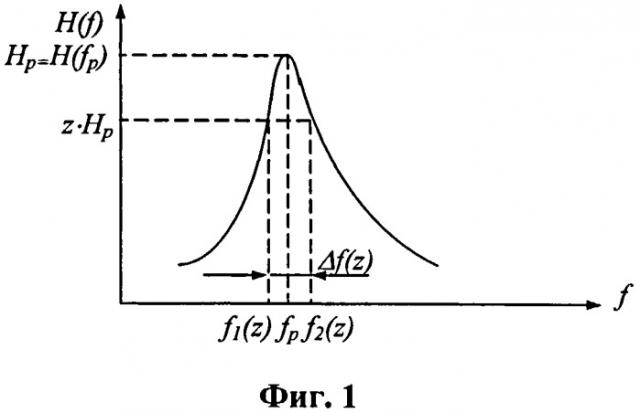
Предлагается способ определения логарифмических декрементов колебаний, по которому гармонической силой (моментом) или ускорением платформы вибростенда постоянной амплитуды и пошагово изменяемой частотой f возбуждают вынужденные колебания испытуемого объекта, измеряют один из кинематических параметров колебаний испытуемого объекта (амплитуды перемещений, скоростей, ускорений или их комплексные отклики), строят по этому параметру резонансные кривые H(f), находят резонансные частоты f_p и высоты резонансных пиков Н_р=H(f_p), определяют характерные частоты f_i(z) и f₂(z)>f₁(z), как частоты точек пересечения резонансной кривой и прямой, проведенной на произвольной высоте z·H_p(z<1,0-величина спада), параллельно оси абсцисс (оси частот), определяют ширину резонансного пика как разность двух характерных частот Δf(z)=f₂(z)-f₁(z), (Фиг.1) и логарифмические декременты колебаний рассчитывают по формулам:

, по амплитудным частотным характеристикам перемещений, скоростей или ускорений;

по квадратурным составляющим комплексных откликов перемещений или ускорений и синфазных составляющих скоростей.

Отличительными признаками изобретения являются следующие: ширину резонансных пиков Δf(z)=f₂(z)-f₁(z) определяют как разность двух характерных частот f₁(z) и f₂(z)>f₁(z), полученных при пересечении резонансных кривых на произвольной высоте z·H_p (z<1,0) прямой, параллельной оси абсцисс (оси частот), и логарифмические декременты колебаний рассчитывают по формулам:

по амплитудным частотным характеристикам перемещений, скоростей или ускорений;

по квадратурным составляющим комплексных откликов перемещений или ускорений и синфазных составляющих скоростей.

В результате поиска по источникам патентной и научно-технической информации решений, содержащих такой признак, не обнаружено. Следовательно, можно сделать заключение о том, что предложенное решение неизвестно до настоящего уровня техники и соответствует критерию охраноспособности - «новое».

Способ может быть осуществлен на образцах материалов, элементах конструкций, на сложных конструкциях с плотным спектром собственных частот при изгибных, крутильных или продольных колебаниях, возбуждаемых силовым или кинематическим способом, и может найти применение в машиностроении, ветроэнергетике, строительстве и т.д., где требуется определять динамические характеристики (частоты, формы и логарифмические декременты колебаний) механических конструкций, в исследовании механических свойств материалов, что позволяет сделать вывод о соответствии критерию «промышленная применимость».

Рассмотрим, например, реализацию способа при изгибных колебаниях летательного аппарата самолетного типа с подвесными двигателями под фюзеляжем. Испытания проводились системой «PRODERA». Возбуждение колебаний осуществлялось электродинамическим вибраторам 20IE 20/С. Измерения колебаний осуществлялись акселерометрами AC-565/1. Первичная информация выдавалась в виде синфазной R_n(f) и квадратурной составляющих комплексных ускорений I_n(f) характеристики виброускорений n(f) [g] в функции частоты/сигналов акселерометров.

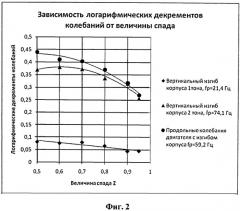
Результаты эксперимента представлены на графиках (Фиг.2) в виде зависимостей логарифмических декрементов колебаний δ oт степени спада z. Величины логарифмических декрементов колебаний, определенные по способу, принятому в качестве прототипа, соответствуют величине δ при z=0,5.

Способ определения логарифмических декрементов колебаний по ширине резонанса равноинтенсивных колебаний, по которому гармонической силой (моментом) или ускорением платформы вибростенда постоянной амплитуды и пошагово изменяемой частотой f возбуждают вынужденные колебания испытуемого объекта, измеряют один из кинематических параметров колебаний испытуемого объекта: амплитуды перемещений, скоростей, ускорений или их комплексные отклики, строят по этому параметру резонансные кривые H(f), находят резонансные частоты f_p и высоты резонансных пиков Н_р=H(f_p), отличающийся тем, что ширину резонансных пиков Δf(z)=f₂(z)-f₁(z) определяют как разность двух характерных частот f₁(z) и f₂(z)>f₁(z), полученных при пересечении резонансных кривых на произвольной высоте z·Hp (z<1,0) прямой, параллельной оси абсцисс (оси частот), и логарифмические декременты колебаний рассчитывают по формулам: по амплитудным частотным характеристикам перемещений, скоростей или ускорений; по квадратурным составляющим комплексных откликов перемещений или ускорений и синфазных составляющих скоростей.