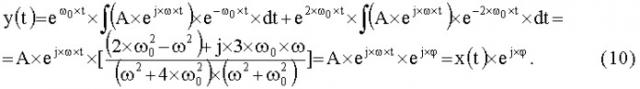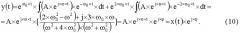Способ определения выходной реакции линейного устройства на входной сигнал

Способ определения выходной реакции линейного устройства на входной сигнал

Иллюстрации

Показать все

Реферат

Изобретение относится к техническим системам, а именно к способам оптимального моделирования устройств электронной техники различного применения - назначения.

В процессе моделирования устройств электронной технике одной из важных проблем является определение выходной реакции линейного устройства y(t) на входной сигнал в виде функции времени x(t), важное значение приобретают способы, позволяющие представить выходную реакцию y(t) в явном виде, то есть в виде функции от входного сигнала x(t).

Известен способ определения выходной реакции линейного устройства y(t) на входной сигнал в виде функции времени x(t), включающий моделирование работы линейного устройства в виде линейного дифференциального уравнения n-го порядка с постоянными коэффициентами a_n-1, …a₁, a₀

d n y ( t ) d t n + a n − 1 × d n − 1 y ( t ) d t n − 1 + … + a 2 × d 2 y ( t ) d t 2 + a 1 × d y ( t ) d t + a 0 × y ( t ) = x ( t ) ,

определение n собственных параметров линейного устройства λ_i (i=1, 2, …n)

путем решения соответствующего характеристического уравнения

λⁿ+a_n-1×λ^n-1+…+a₂×λ²+a₁×λ+a₀=0

и представления его в виде

(λ-λ_n)×(λ-λ_n-1)×…×(λ-λ₂)×(λ-λ₁)=0,

последующее определение реакции линейного устройства

y ( t ) = C n ( t ) × e λ n × t + C n − 1 ( t ) × e λ n − 1 × t + … + C 2 ( t ) × e λ 2 × t + C 1 ( t ) × e λ 1 × t ,

где C_n(t), C_n-1(t), …C₂(t), C₁(t) - варьируемые коэффициенты, которые определяются из решения системы n дифференциальных уравнений [1, стр.118]

d C n ( t ) d t × e λ n × t + d C n − 1 ( t ) d t × e λ n − 1 × t + … + d C 2 ( t ) d t × e λ 2 × t + d C 1 ( t ) d t × e λ 1 × t = 0 ,

λ n × d C n ( t ) d t × e λ n × t + λ n − 1 × d C n − 1 ( t ) d t × e λ n − 1 × t + … + λ 2 × d C 2 ( t ) d t × e λ 2 × t + λ 1 × d C 1 ( t ) d t × e λ 1 × t = 0 ,

λ n 2 × d C n ( t ) d t × e λ n × t + λ n − 1 2 × d C n − 1 ( t ) d t × e λ n − 1 × t + … + λ 2 2 × d C 2 ( t ) d t × e λ 2 × t + λ 1 2 × d C 1 ( t ) d t × e λ 1 × t = 0 ,

λ n n − 1 × d C n ( t ) d t × e λ n × t + λ n − 1 n − 1 × d C n − 1 ( t ) d t × e λ n − 1 × t + … + λ 2 n − 1 × d C 2 ( t ) d t × e λ 2 × t + λ 1 n − 1 × d C 1 ( t ) d t × e λ 1 × t = x ( t )

Недостатками этого способа являются:

во-первых, невозможность представить окончательное решение в явном виде, то есть в виде функции от входного сигнала x(t),

во-вторых, невозможность его применения при моделировании работы линейного устройства в виде линейного дифференциального уравнения n-го порядка с переменными коэффициентами.

Известен способ определения выходной реакции линейного устройства y(t) на входной сигнал в виде функции времени x(t), включающий моделирование работы линейного устройства в виде линейного дифференциального уравнения n-го порядка с постоянными коэффициентами a_n-1, ... a₂, a₁, a₀

d n y ( t ) d t n + a n − 1 × d n − 1 y ( t ) d t n − 1 + … + a 2 × d 2 y ( t ) d t 2 + a 1 × d y ( t ) d t + a 0 × y ( t ) = x ( t ) ,

определение n собственных параметров линейного устройства λ_i (i=1, 2, …n) путем решения соответствующего характеристического уравнения

λⁿ+a_n-1×λ^n-1+…+a₂×λ²+a₁×λ+a₀=0

и представления его в виде

(λ-λ_n)×(λ-λ_n-1)×…×(λ-λ₂)×(λ-λ₁)=0,

последующее определение реакции линейного устройства

y{t)=L^-1{Y(p)}

путем использования обратного преобразования Лапласа L^-1{∗} от функции

Y ( p ) = X ( p ) ( p − λ n ) × ( p − λ n − 1 ) × … × ( p − λ 2 ) × ( p − λ 1 ) ,

где функция комплексной переменной X(p) определяется путем прямого преобразования Лапласа L{∗}

X ( p ) = L { x ( t ) } = ∫ 0 ∞ x ( t ) × e − p × t × d t

функции x(t) [1, стр.129].

Этот способ отчасти позволяет представить окончательное решение в явном виде.

Однако при этом

во-первых, необходимо применять сложные преобразования из области вещественной переменной в область комплексной переменной и обратно,

во-вторых, как и предыдущий способ, его нельзя применять при моделировании работы линейного устройства в виде линейного дифференциального уравнения n-го порядка с переменными коэффициентами.

Техническим результатом изобретения является упрощение способа определения выходной реакции линейного устройства на входной сигнал в виде функции времени и расширение функциональных возможностей в случае моделирования линейного устройства в виде дифференциальных уравнений с переменными коэффициентами.

Указанный технический результат достигается тем, что в известном способе определения выходной реакции линейного устройства на входной сигнал в виде функции времени, включающим моделирование работы линейного устройства в виде линейного дифференциального уравнения порядка n с постоянными коэффициентами, определение n собственных параметров линейного устройства λ_i, при этом i равно 1, 2, …n, последующее собственно определение реакции линейного устройства на входной сигнал.

В котором собственно определение реакции линейного устройства на входной сигнал осуществляют для каждого с номером i собственного параметра линейного устройства путем умножения входного сигнала на экспоненциальную функцию времени с отрицательным знаком при каждом с номером i собственном параметре линейного устройства, полученное произведение интегрируют по времени, результат интегрирования по времени умножают на экспоненциальную функцию времени с положительным знаком при каждом с номером i собственном параметре, далее полученные произведения для каждого с номером i собственного параметра линейного устройства суммируют с соответствующими весовыми множителями по всем n собственным параметрам линейного устройства.

Раскрытие сущности заявленного изобретения.

Заявленная совокупность существенных признаков способа определения выходной реакции линейного устройства на входной сигнал в виде функции времени, а именно когда:

собственно определение реакции линейного устройства на входной сигнал осуществляют для каждого с номером i собственного параметра линейного устройства путем умножения входного сигнала на экспоненциальную функцию времени с отрицательным знаком при каждом с номером i собственном параметре линейного устройства,

полученное произведение интегрируют по времени,

результат интегрирования по времени умножают на экспоненциальную функцию времени с положительным знаком при каждом с номером i собственном параметре,

далее полученные произведения для каждого с номером i собственного параметра линейного устройства суммируют с соответствующими весовыми множителями по всем n собственным параметрам линейного устройства.

Это обеспечит:

во-первых, возможность представления выходной реакции линейного устройства в явном виде и тем самым - упрощение представления выходной реакции линейного устройства - и тем самым упрощение способа определения выходной реакции линейного устройства на входной сигнал.

во-вторых, возможность моделирования линейного устройства в виде дифференциальных уравнений с переменными коэффициентами и, как следствие, расширение функциональных возможностей способа.

Рассмотрим моделирование работы линейного устройства, полученное расчетно-экспериментальным путем, в виде известного линейного дифференциального уравнения n-го порядка с постоянными коэффициентами a_n-1, ... a₁, a₀

d n y ( t ) d t n + a n − 1 × d n − 1 y ( t ) d t n − 1 + … + a 2 × d 2 y ( t ) d t 2 + a 1 × d y ( t ) d t + a 0 × y ( t ) = x ( t ) ,           (1)

с последующим определением n собственных параметров линейного устройства λi (i=1, 2, …n) путем решения соответствующего характеристического уравнения

λ n + a n − 1 × λ n − 1 + … + a 2 × λ 2 + a 1 × λ + a 0 = 0                                  (2)

и представления его в виде

(λ-λ_n)×(λ-λ_n-1)×…×(λ-λ₂)×(λ-λ₁)=0.

Согласно заявленному способу, запишем это дифференциальное уравнение n-го порядка с постоянными коэффициентами a_n-1, …a₁, a₀ с использованием найденных корней характеристического уравнения в виде системы n дифференциальных уравнений первого порядка

d y ( t ) d t − λ 1 × y ( t ) = g 1 ( t ) , d g 1 ( t ) d t − λ 2 × g 1 ( t ) = g 2 ( t ) , d g n − 2 ( t ) d t − λ n − 1 × g n − 2 ( t ) = g n − 1 ( t ) , d g n − 1 ( t ) d t − λ n × g ( t ) n − 1 = x ( t ) .                        (3)

Решение последнего (n-го) уравнения системы (3) имеет вид

g n − 1 ( t ) = Ф n ( t ) ,                                     (4)

где функция Φ_n(t) для n-го собственного параметра линейного устройства находится из выражения

Ф n ( t ) = e λ n × t × ∫ x ( t ) × e − λ n × t × d t ,                                     (5)

при этом функция времени x(t) умножается на экспоненциальную функцию времени с отрицательным знаком при n-м собственном параметре линейного устройства, полученное произведение интегрируется по времени, результат умножается на экспоненциальную функцию времени с положительным знаком при n-м собственном параметре линейного устройства.

Подставляя полученное решение g_n-1(t) в предпоследнее уравнение системы (10) и решая его, получим выражение

g n − 2 ( t ) = e λ n − 1 × t × ∫ g n − 1 ( t ) × e − λ n − 1 × t × d t .                             (6)

Подставляя в формулу (6) выражения (4) и (5) и проводя интегрирование по частям, получаем

g n − 2 ( t ) = e λ n − 1 × t × ∫ g n − 1 ( t ) × e − λ n − 1 × t × d t = e λ n − 1 × t × ∫ [ e λ n × t ∫ x ( t ) × e − λ n × t × d t ] × e − λ n − 1 × t × d t = = e λ n − 1 × t × 1 ( λ n − 1 − λ n ) × [ e ( λ n − λ n − 1 ) × t × ∫ x ( t ) × e − λ n × t × d t − ∫ e ( λ n − λ n − 1 ) × t × x ( t ) × e − λ n × t × d t ] .

Или окончательно

g n − 2 ( t ) = Ф n ( t ) λ n − λ n − 1 + Ф n − 1 ( t ) λ n − 1 − λ n .                                           (7)

Поступая аналогичным образом с последующими уравнениями системы (3), получаем окончательное выражение для реакции линейной системы в виде

y ( t ) = ∑ i = 1 n β i × Ф i ( t ) = ∑ i = 1 n β i × [ ( e t ) λ i × ∫ x ( t ) × ( e t ) − λ i × d t ] ,                                     (8)

где β_i - весовые множители, равные

β i = 1 ∏ k = 1, k ≠ i n ( λ i − λ k ) ,                                              (9)

где i=1, 2, …n, а произведение разностей между собственными параметрами линейного устройства (λ_i-λ_k) вычисляются для всех k от 1 до n за исключением значения k=i.

При моделировании линейного устройства в виде дифференциальных уравнений с переменными коэффициентами можно представить дифференциальное уравнение в виде

t 2 × d 2 y ( t ) d t 2 + a 1 × t × d y ( t ) d t + a 0 × y ( t ) = x ( t ) ,

решить записанное для него характеристическое уравнение

λ²+(a₁-1)×λ+a₀=0

и определить его корни: λ₁ и λ₂.

В процессе определения реакции линейного устройства для каждого i-го собственного параметра линейного устройства функция времени x(t) умножается на экспоненциальную функцию времени с отрицательным знаком при n-м собственном параметре линейного устройства, полученное произведение интегрируется по времени, результат умножается на экспоненциальную функцию времени с положительным знаком при n-м собственном параметре линейного устройства, полученные произведения суммируются с соответствующими весовыми множителями по всем n собственным параметрам линейного устройства.

y ( t ) = ∑ i = 1 2 β i × [ ( e I n   t ) λ i × ∫ x ( t ) × ( e I n  t ) − λ i × d t ] .

Пример конкретной реализации способа определения выходной реакции линейного устройства на входной сигнал.

Рассмотрим реализацию заявленного способа определения выходной реакции линейного устройства на входной сигнал на примере фазовращателя СВЧ.

На вход фазовращателя СВЧ подают сигнал в виде гармонической функции времени x(t)=A×e^{j× ω×t}, где

ω - круговая частота, A - амплитуда, j = − 1 - мнимая единица.

Моделируют работу фазовращателя СВЧ (линейного устройства) дифференциальным уравнением (1) второго порядка (n=2) с постоянными коэффициентами

a₁=-3×ω₀, a₀=2×ω₀,

где ω₀ - значение круговой частоты в центре рабочей полосы частот.

Определяют n собственных параметров линейного устройства λ₁=ω₀ и λ₂=2xω₀ посредством решения характеристического уравнения (2).

Далее собственно определяют реакцию линейного устройства на входной сигнал для каждого i-го собственного параметра линейного устройства путем умножения входного сигнала на экспоненциальную функцию времени с отрицательным знаком при каждом i-м собственном параметре линейного устройства, полученное произведение интегрируют по времени, результат интегрирования по времени умножают на экспоненциальную функцию времени с положительным знаком при каждом i-м собственном параметре, полученные произведения для каждого i-го собственного параметра линейного устройства суммируют с соответствующими весовыми множителями по всем n собственным параметрам линейного устройства, что в конечном итоге выражено формулой (8)

y ( t ) = e ω 0 × t × ∫ ( A × e j × ω × t ) × e − ω 0 × t × d t + e 2 × ω 0 × t × ∫ ( A × e j × ω × t ) × e − 2 × ω 0 × t × d t = = A × e j × ω × t × [ ( 2 × ω 0 2 − ω 2 ) + j × 3 × ω 0 × ω ( ω 2 + 4 × ω 0 2 ) × ( ω 2 + ω 0 2 ) ] = A × e j × ω × t × e j × ϕ = x ( t ) × e j × ϕ .              (10)

Согласно этой формуле, реакция фазовращателя СВЧ (линейного

устройства) на входной сигнал:

во-первых, повторяет входной сигнал в виде функции времени x(t), во-вторых, имеет не зависящий от времени набег фазы φ, величина которого рассчитывается по формуле, полученной из выражения (10)

ϕ = a r c t g [ 3 × ω 0 × ω ( 2 × ω 0 2 − ω 2 ) ] ,                                                  (11)

где arctg(z) - функция, обратная тригонометрическому тангенсу.

Итак, набег фазы является основным и единственным параметром, характеризующим реакцию фазовращателя СВЧ на входной гармонический сигнал, и он однозначно представляется в виде математической формулы, то есть в явном виде.

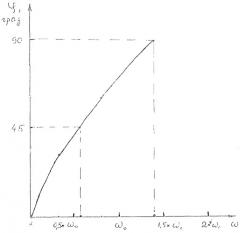
На фиг.1 приведены вычисленные по формуле (11) значения набега фазы фазовращателя СВЧ для разных значений круговой частоты.

Из фиг.1 видно, что на частоте ω = 17 − 3 2 × ω 0 = 4,12 × ω 0 набег фазы составляет ϕ = π 4 = 45 ∘ , а на частоте ω = 2 × ω 0 = 1,41 × ω 0 набег фазы составляет ϕ = π 2 = 90 ∘ .

Таким образом, заявленный способ определения выходной реакции линейного устройства на входной сигнал позволит по сравнению с прототипом:

во-первых, упростить способ благодаря представлению выходной реакции линейного устройства в явном виде,

во-вторых, расширить его функциональные возможности благодаря возможности моделирования линейного устройства в виде дифференциальных уравнений с переменными коэффициентами.

Источники информации

1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969 г., стр.129 - прототип.

Способ определения выходной реакции линейного устройства на входной сигнал в виде функции времени, включающий моделирование работы линейного устройства в виде линейного дифференциального уравнения порядка n с постоянными коэффициентами, определение n собственных параметров линейного устройства λ_i, при этом i равно 1, 2, …, n, последующее собственно определение реакции линейного устройства на входной сигнал, отличающийся тем, что собственно определение реакции линейного устройства на входной сигнал осуществляют для каждого с номером i собственного параметра линейного устройства путем умножения входного сигнала на экспоненциальную функцию времени с отрицательным знаком при каждом с номером i собственном параметре линейного устройства, полученное произведение интегрируют по времени, результат интегрирования по времени умножают на экспоненциальную функцию времени с положительным знаком при каждом с номером i собственном параметре, далее полученные произведения для каждого с номером i собственного параметра линейного устройства суммируют с соответствующими весовыми множителями по всем n собственным параметрам линейного устройства.