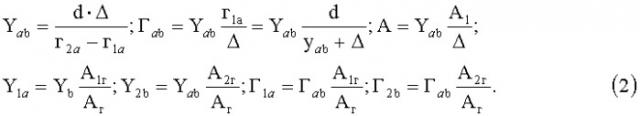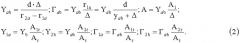Оптический способ измерения размеров и положения объекта и дальномер-пеленгатор

Оптический способ измерения размеров и положения объекта и дальномер-пеленгатор

Иллюстрации

Показать все

Реферат

Изобретение относится к области определения взаимного положения объектов, один из которых служит источником электромагнитного излучения в оптическом диапазоне, а второй - его измерителем, и может использоваться для создания оптических дальномеров, пеленгаторов, теодолитов, телескопов и другой оптической аппаратуры аналогичного назначения. Способ может быть использован для определения формы поверхности объекта на большом расстоянии с заданной относительной погрешностью.

Известен фотограмметрический способ измерений отстояния объекта [1], выбранный в качестве аналога, включающий получение двух отображений объекта на плоскостях измерений, ортогональных оптическим осям идентичных устройств, расположенных на известной базе, измерение координат отображений граничных точек объекта на осях плоскостных систем координат, определение расстояния до объекта, используя как опорный параметр расстояние от точки расположения оптического устройства до плоскости измерений.

Известен оптический способ измерения размеров и положения объекта [2], выбранный в качестве прототипа, включающий измерение в парной проективной системе координат (получение двух отображений объекта на плоскостях измерений, ортогональных оптическим осям идентичных устройств, расположенных на известной базе, управление размером базы и расстоянием от центра проектирования до плоскости измерений, измерение положения отображений граничных точек объекта на осях парной проективной системы координат, определение расстояния до объекта, используя как опорные параметры базу измерений и расстояние от центра проектирования до плоскости измерений) и вычисление по полученным оценкам размеров объекта и его положения.

Дальномер-пеленгатор [2], выбранный в качестве прототипа, состоящий из двух параллельных оптических устройств, установленных на базе, двух измерительных плоскостей, механизма поворота базы по двум осям, устройства изменения размеров базы и отстояния измерительной плоскости от центров оптических устройств, систем переноса отображений на плоскости измерений, блока управления и блока вычислений, блок управления подключен к механизмам поворота базы по двум осям и к устройствам изменения длины базы и отстояния измерительных плоскостей от центров оптических устройств, а измерительные плоскости в виде матриц установлены на общей плоскости, параллельной базе, выходы которых подключены к вычислительному устройству.

Недостатки способа и реализующего его устройства связаны с недостаточной точностью измерений размеров и положения объекта.

Целью заявляемого изобретения является повышение точности и разрешающей способности определения размеров объекта и его положения относительно измерителя по результатам измерений их отображений в парной проективной системе координат, а также создания устройства, обеспечивающего повышение качества (разрешающей способности измерений), при измерении удаленных и малых объектов.

Указанная цель достигается тем, что в оптическом способе измерений размеров и положения объекта, включающем измерение в парной проективной системе координат (получение двух отображений объекта на плоскостях измерений, ортогональных оптическим осям идентичных устройств, расположенных на известной базе, управление размером базы и расстоянием от центра проектирования до плоскости измерений, измерение положения отображений граничных точек объекта на осях парной проективной системы координат) и вычисление по полученным данным размеров объекта и его положения, используя как опорные параметры базу измерений и расстояние от центра проектирования до плоскости измерений, дополнительно выполняют измерение его отображений в дополнительной зеркальной парной проективной системе координат (измерение в двойной парной проективной системе координат).

Указанная цель достигается также тем, что в способе по п.1 разбивают проекции отображения объекта, полученные на осях зеркальной системы координат, опорной мерой, равной расстоянию от центра проектирования до плоскости измерений, максимальное число делений транслируют на все другие проекции путем проведения через точки деления прямых, параллельных гипотенузам, соединяющим концы полученных проекций на ортогональных осях зеркальной системы координат, в том числе и на опорную меру измерений, получая новую опорную меру, вычисляют индивидуальные меры измерений для каждой из проекций, повторяют процесс разделения проекций отображений вновь полученной мерой до получения требуемой разрешающей способности (меры) измеряемых размеров объекта, а требуемые размеры объекта и его положения определяют произведением индивидуальной меры измерений каждой проекции на транслируемое число делений.

Указанная цель достигается также тем, что дальномер-пеленгатор, состоящий из двух параллельных оптических устройств, установленных на базе, двух измерительных плоскостей, механизма поворота базы по двум осям, устройств управления изменением размеров базы и отстояния измерительной плоскости от центров оптических устройств, систем переноса отображений на плоскости измерений, блока управления и блока вычислений, блок управления подключен к механизмам поворота базы по двум осям и устройствам изменения длины базы и отстояния измерительных плоскостей от центров оптических устройств, а измерительные плоскости в виде матриц установлены на общей плоскости, параллельной базе, выходы которых подключены к вычислительному устройству, дополнительно установлены две параллельные матричные измерительные плоскости на той же базе, но ортогональные первой, чувствительные поверхности которых обращены друг к другу, выходы которых подключены к вычислительному устройству.

Пример выполнения заявляемого изобретения

На фиг.1 показана двойная парная проективная система координат и способ измерений в ней.

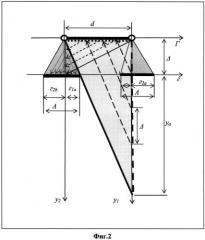
На фиг.2 показан способ трансляции числа делений в двойной парной проективной системе координат

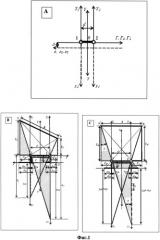
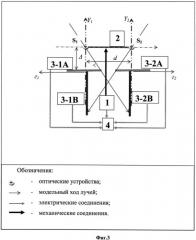
На фиг.3 показана структурная блок схема дальномера-пеленгатора.

Дальномер-пеленгатор, показанный на фиг.3, состоит из пульта управления 1, двух идентичных оптических устройств S₁, S₂, размещенных на базе 2, в плоскости которой установлены матричные измерительные плоскости для каждого оптического устройства 3-1A, 3-1B, 3-2A, 3-2B соответственно, и вычислительного устройства 4. Механизмы поворота базы по двум осям, устройства управления изменением размеров базы и отстояния измерительной плоскости от центров оптических устройств, системы переноса отображений на плоскости измерений и блок управления не показаны, так как они выполняют свои функции в соответствии с назаначением.

Пульт управления 1 (вычислительное устройство), выполнен в виде в виде микропроцессора, например семейства AVR фирмы АТМЕС, обеспечивающего управление механизмами вращения базы по двум осям, изменения размеров базы, изменения расстояния от измерительных плоскостей до оптических устройств.

База 2 - жесткое основание, имеющее механизмы: вращения по двум ортогональным осям и изменения длины базы. На концах базы установлены оптические устройства S₁, S₂ с измерительными плоскостями, ортогональными 3-1A, 3-2A и параллельными 3-1B, 3-2B их оптическим осям. Измерительные плоскости 3-1А, 3-1B, 3-2A, 3-2B выполнены в виде идентичных матричных плоскостей, требуемой дискретности, например 100 точек на 1 мм, на которые проектируются отображения объектов и оптические оси устройств S₁ и S₂. Поверхности измерительных плоскостей 3-1А, 3-2А установлены параллельно направлению базы на отстоянии Δ. С этими сторонами связаны направления измерительных осей г₁ и г₂ соответственно. Поверхности измерительных плоскостей 3-1B, 3-2B установлены ортогонально направлению базы по направлению оптических осей устройств S₁ и S₂ и обращены чувствительными сторонами навстречу друг другу. С этими сторонами связаны направления измерительных осей y₁ и y₂ соответственно. Вычислительное устройство 4 выполнено в виде микропроцессора, например семейства AVR фирмы АТМЕС.

Дальномер-пеленгатор работает следующим образом. Оператор наблюдает ряд объектов, имеющих отображения от двух оптических устройств S₁, S_2, и выбирает одно из них для оценки его положения и размеров. При этом оптические устройства имеют параллельные оптические оси и перекрывающиеся сектора обзора. Установленные размеры базы d и ее отстояния от плоскости измерений Δ поступают с пульта управления 1 в вычислитель 4, для оценки опорного параметра.

Лучи света от объекта попадают в оптические устройства S₁ и S₂ и проектируются на плоскости 3-1A, 3-1B, 3-2A, 3-2B. С матриц измерительных плоскостей снимают информацию по строкам, совпадающим с направлением измерительных осей г₁ и г₂ и y₁ и y₂, в которых участки засветки преобразуются в электрические сигналы, поступающие в вычислитель 4. В вычислителе 4 определяют отстояние и размеры объекта по осям ГY (Г₁, Г₂ и Y₁, Y₂). При необходимости для повышения разрешающей способности изменяют размер d базы 2 (изменяется масштаб отображения на оси y) и отстояние Δ оптических устройств S₁, S₂ от измерительных плоскостей (изменяется мера отображения на оси y).

Парная проективная система координат, имеющая дополнительные зеркальные оси показана на фиг.1A. Она имеет две совмещенные проективные системы: внешнюю и внутреннюю. Для измерения внешней информации используются системы координат: ГY; Г₁Y₁; Y₂Г₂, оси наблюдений Y₁Y₂ которых могут быть совмещены с осями оптических устройств. Отображения объекта получают на внутренней системе координат: гy; г₁y₁; г₂y₂. При этом системы координат (Г₁Y₁; Y₂Г₂) и (г₁y₁; г₂y₂) являются зеркальными и центрированными относительно центра 0, имея постоянное смещение Δ, заданное отстоянием центра проектирования от плоскости измерений. При этом, когда на оси г объект отображается в функции тангенса от «параллактического» угла γ, то на оси y - в функции котангенса. Получили двойную парную проективную систему координат.

Процесс построения отображений в двойной парной проективной системе координат при произвольном положении объекта, когда он наблюдается двумя измерителями показан на фиг.1B.

Объект длиной A в виде прямой линии ab отображен в двойной парной проективной системе координат (ГY; Г₁Y₁; Y₂Г₂, (гy; г₁y₁; г₂y₁), построенных на центрах проектирования 1 и 2.

Проекции его внешнего положения на осях Г₁; Г₂ и Y₁; Y₂ равны: Г_1a; Г_2b; Y_1a; Y_2b.

Проекции отображений объекта и его положения на осях координат г₁y₁; г₂y₂ (показаны на фиг 1B не все, чтобы не перегружать отображение) равны: A_1г; A_2г; г_1a; г_2a; г_1b; г_2b; y_1a; y_2а.

Известны и постоянны на время получения отображений два параметра: Δ, d и измерены следующие 8 параметров: г_1a; г_2a: г_1b; г_2b; y_1a, y_2а, А_1г, А_2г. Необходимо определить размеры A и его положение: Y_1a, Y_2b, Г_1a, Г_2b.

Двойная парная проективная система координат обладает симметрией результатов проектирования относительно центра 0, что позволяет использовать принцип центрирования результатов измерений (суммирования симметричных отображений) при наличии всех необходимых измерений.

Тогда получим 5 осредненных оценок проекций в системе координат гy и 2 оценки в системе координат ГУ, что соответствует модели, показанной на фиг.1B:

; ; ;

г_1a+г_2a=г_1b+г_2b=A₁=A₂; A_1y=A_2y=y_ab

; .

В результате система уравнений, необходимая для определения требуемых параметров, существенно упрощается (Фиг.1C):

Она имеет следующие решения:

Параметр Y_ab является опорным во внешней системе координат ГY; Г₁Y₁; Г₂Y₂, по которому можно оценить все другие параметры, на основе их изменений относительно среднего, а следовательно, и задает и погрешности их определений.

Параметр y_ab является опорным во внутренней системе координат гy; г₁y₁; г₂y₂, который определяет оценки отображений и относительные погрешности всех измеряемых и вычисляемых параметров.

Связь между внутренней и внешней системами координат определяется результатами измерений 4-х параметров: d, Δ, г_1a; г_2a.

Использование результатов измерений параметров y_1a; y_2a обеспечивает существенное повышение ориентационной направленности осей наблюдений на объект. Главный недостаток решения данной системы в том, что при нахождении объекта на большом отстоянии (параллактический угол мал - менее 1') величины г_1a; г_2a; (г_1b; г_2b; A_1г; A_2г) являются малыми, а их разность является очень малой величиной, что обуславливает низкую разрешающую способность (точность) оценки искомых величин.

Для повышения точности оценки отображений требуемых параметров необходимо использовать те результаты отображения, которые можно измерить с наименьшей относительной погрешностью. Этой возможностью обладают проекций на осях y₁ и y₂. Коэффициент повышения точности от использования проекций на осях y₁ и y₂ вместо г₁ и г₂ оценим по сравнению проекций. Луч 1a на оси г отображается отрезком г_1a, а на оси y₁ - отрезком y_1a. Тогда коэффициент усиления за счет использования отрезка y_1a вместо г_1a, будет равен:

.

Обычно отношение отображений d/Δ>10³, а ctgγ<3°, то k>10⁶. То есть правильное использование двойной парной системы координат позволяет получить коэффициент усиления отображения порядка 10⁶. Однако прямая реализация этого достоинства оказалась невозможной.

Повышение оценки искомых величин возможно только при повышении разрешающей способности измерений 4-х параметров: d, Δ, г_1a; г_2a.

Для обеспечения требуемой разрешающей способности оценки отображения объекта представим любую прямую линию A, состоящей из двух параметров: меры отображения (Δ_a) и числа частей (n_a), заключенных в этой прямой:

Δ_a·n_a=A.

Тогда относительная погрешность и масштаб отображения прямой линии определяется выражениями:

ε_a=Δ_a/a=Δ_a/(n_a·Δ_a)=1/n_a

M_a=a/Δ_a=n_a ε_a·M_a=1,

где M_a - масштаб отображения прямой при измерении его мерой Δ_a;

Δ_a - мера или разрешающая способность измерений;

ε_a - относительная погрешность измерений прямой A.

Если все стороны объекта будут измерены с одинаковой относительной погрешностью, то отображение формы объекта будет достоверно. Следовательно, для обеспечения достоверности отображения всех сторон объекта необходимо, чтобы все стороны и их проекции на разные оси координат имели равное количество мерных частей. Тогда длина любой проекции формы объекта должна состоять из равного количества мерных частей (n), но каждая проекция будет иметь свою меру отображения. И именно меру отображения необходимо определять для оценки длины каждой стороны объекта и определять ее длину путем умножения меры на необходимое число мерных частей (n). Этот метод измерений будем называть методом равных относительных погрешностей.

Величины Δ_a и n_a являются числами, к каждому из которых применимы все законы арифметических действий: сочетательности, переместительности, монотонности, дистрибутивности [1,4]. А для всех построенных геометрических фигур сохраняются условия их конгруэнтности, так как произведение М·ε=1. (Две фигуры называются конгруэнтными или равными, если существует изометрия плоскости, которая переводит одну в другую.)

То есть геометрические отношения между прямыми линиями и фигурами, установленные для условия постоянства меры измерений, сохраняются при условии постоянства числа делений в отрезках.

Но изменение числа делений в отрезке приводит к обратной зависимости при установлении меры отображения (разрешающей способности) по каждой из осей координат.

В парной проективной системе координат большинство проекций сторон объектов представляют прямоугольные треугольники, катеты которых параллельны, и их можно рассматривать как проекции на соответствующие оси системы координат (фиг.2).

В парной проективной системе координат в качестве масштаба отображения на осях y₁y₂ используют размер базы d, а в качестве цены деления меры - ее ширину Δ.

Процесс измерений проекций на осях системы координат постоянной мерой общепринят, в нем число делений определяет размер проекции. В этом случае процесс деления и измерения неразделимы. В нем меру будем обозначать значком Δ, а число делений, равное измеренной величине, будем обозначать знаком n со значком, характеризующим проекцию на ось и обозначение прямой, например:

a _Г=n_Гa·Δ; a _Y=n_Ya·Δ.

Процесс отображения - измерения проекций на осях системы координат с постоянным числом делений в настоящее время не используется, поэтому рассмотрим его реализацию при выполнении измерений.

Процесс отображения длины отрезка Δ, имеющего две проекции на ортогональные оси координат, состоит из трех этапов:

1. - этапа определений числа частей в проекциях на осях координат при выполнении измерений опорной мерой Δ и определения максимального числа частей (фиг.1A);

2. - этапа передачи максимального числа частей на все проекции прямых, участвующие в определении требуемых отображений (фиг.2);

3. - этапа определения меры отображения в проекциях прямых, реализуемой при выполнении измерений с постоянным числом частей.

Для передачи числа делений с одного катета прямоугольного треугольника на другой необходимо провести через меры делений одного катета прямые, параллельные гипотенузе, что обеспечит равное число делений на другом катете и измерение на двух катетах с равной относительной погрешностью, но разной мерой. Меры отображения на каждом катете будут прямо пропорциональны числу делений катетов при измерении постоянной мерой. В процессе передачи числа делений их будем обозначать знаком N, а меру отображения, равную определенной величине, будем обозначать знаком m со значком, характеризующим проекцию на ось и обозначение прямой, например:

a _Г=m_Гa·N; a _Y=m_Ya·N.

Если проекции прямой A на осях координат имеют две разные оценки, тогда:

a _Г=n_Гa·Δ=m_Гa·N; и при трансляции частей: ;

а при трансляции мер: .

Мера отображения прямой A определяется на основе мультипликативной зависимости:

Поэтому при использовании метода равных относительных погрешностей в каждом прямоугольном треугольнике количество мерных частей (N) для катетов постоянно. При этом величина этих мер (разрешающая способность) для каждой из сторон будет своя (m_i) и она прямо пропорциональна числу делений измеренных постоянной мерой.

Если все стороны треугольника во внутренней системе координат (гy₁y₂) измерены постоянной относительной погрешностью, то его отношения подобия с внешними треугольниками приведут к оценке внешних размеров с той же постоянной относительной погрешностью, меры измерений которых определяются из выражения:

,

где Y_ab - мера отрезка Y_ab, имеющего число частей, равное N;

m_d, m_Δ, m_г1a, m_г2a - меры отрезков d, Δ, г_1a, г_2a, имеющих число частей, равное N соответственно;

n_d, n_Δ, n_г1a, n_г2a - число частей в отрезках, измеренных постоянной мерой.

Сущность метода равных относительных погрешностей заключена в том, что при проектировании отображений объекта меры измерений его сторон транслируются одновременно с его сторонами и, наоборот, при измерении проекций отображения их меры переносятся через подобие треугольников в разрешающие способности измерений объекта, а измеряют малые отображения и получают на объекте, находящемся на очень большом отстоянии, среднее значение функции - меры на большом отрезке пространства. Метод позволяет уменьшить меру измерений пространства внутренней системы координат до величин, которые физически и реализовать невозможно.

Измерим (фиг.2) катеты треугольника (y_a и d) одной мерой Δ, при этом меньшая сторона d будет иметь n_d частей, а большая сторона (y_a+Δ)-N частей. Сторона d будет оценена с большей относительной погрешностью, чем y_a+Δ>>d. Перенесем число делений с катета (y_a+Δ) на катет d, тогда:

y_a+Δ=Δ·(N+1) и d=Δ·n_d=m_d(N+1); n_d<<N.

Для измерения катета d с той же относительной погрешностью, что и катет (y_a+Δ), необходимо провести прямые, параллельные гипотенузе, и тогда на катете d отложится столько же делений, что и на катете (y_a+Δ), то есть (N+1). Эти действия позволяют изменить меру (разрешающую способность) m_d измерений катета d, величина которой определяется из выражения:

m_d·(N+1)=Δ·n_d; m d = Δ ⋅ n d N ​ + 1 и m_d<<Δ.

Коэффициент уменьшения меры m_d или повышения разрешающей способности измерений катета d равен:

k = n d N + 1 ,

где n_d - число частей на катете d при измерении мерой Δ.

Таким образом, катет d может быть оценен разрешающей способностью m_d, в k раз большей разрешающей способности, чем обеспечивает мера измерений Δ. Этой же относительной погрешностью необходимо измерить проекции г_1a, г_2a, Δ.

Для этого через точки деления отрезка d мерой m_d проводим параллельные гипотенузе отрезки на ширину базы Δ, тогда:

Δ·1=m_Δ·(N+1); m Δ = Δ N ​ + 1 .

После этого транслируем число частей параллельно гипотенузам с ширины базы Δ на отрезки г_1a, г_2a. При этом количество частей на этих отрезках возрастет, а меры уменьшатся (ход деления показан стрелками на фиг.2):

; ;

; ;

То есть во внутренней системе координат все стороны в треугольниках имеют равные число частей и имеют отличия только в размерах мер измерений, что позволяет использовать зависимость (5):

Мера измерений отстояний объекта от измерителей уменьшилась в (N+1) раз относительно используемой Δ, а число частей столько же раз увеличилось.

Определим длину отрезка Y_ab:

Таким образом, отстояние объекта по оси Y осталась без изменений, но оно измерено с большей разрешающей способностью в (N+1) раз. После выполнения первого цикла отображений, его можно повторять несколько раз, до получения требуемой разрешающей способности отображений размеров объекта или его положения:

,

где к=1, 2, 3…n - коэффициент повторных делений.

С этой же относительной погрешностью могут быть оценены все требуемые параметры по зависимостям (3).

Это позволяет при произвольной ориентации объекта для каждой из сторон определить необходимую меру в ее конкретном положении для получения оценки ее длины с заданной относительной погрешностью.

Измерив полученные отображения объекта требуемой мерой на каждом участке, получим в результате объект, все стороны которого оценены постоянной относительной погрешностью, то есть достоверное отображение формы объекта и его положения.

Например, если необходимо измерить объект размером D=10 м на расстоянии Y_ab=100 км: tgγ≈10^-4. Проекция его размера на оси г будет равна 10^-3 м, для обеспечения разрешающей способности объекта 1 м она должна содержать порядка 1000 частей, то есть мера ее измерений должна быть m_г≤10^-7. Используем измеритель с Δ=10^-2 м, d=10^-1 м, которые можно изменять, и осью y=100 м, имеющий матрицу с разрешающей способностью m=10^-4 м. Обеспечим отображение проекции объекта на оси y=100 м, изменив до d=10^-2 м.

Определим коэффициент уменьшения меры y/Δ-(N+1)=10⁴, тогда меры отображения составят: m_d≈10^-6 м, m_Δ≈10^-6 м.

Когда к=2, то (N+1)²=10⁸, а мера отображения базы составит m_d≈m_Δ≈10^-10 м. Тогда высота Y_B будет иметь столько же частей, как и катет d, а ее мера будет пропорциональна отношению :

при к=1 m Y b ≈ d ⋅ Δ г 1 b ⋅ ( N + 1 ) ≈ 10   м , ε=10^-6;

при к=2 m Y b ≈ d ⋅ Δ г 1 b ⋅ ( N + 1 ) 2 ≈ 10 − 3   м , ε=10^-8.

Использование предлагаемого способа обеспечивает измерение объектов, наблюдаемый размер которых менее одной угловой минуты: это малые космические объекты, самолеты, ракеты, которые другие способы измерений обеспечить не могут. Способ может быть использован для определения формы поверхности объекта на большом расстоянии с заданной относительной погрешностью.

Предлагаемое техническое решение является новым, поскольку из общедоступных сведений неизвестна двойная парная проективная система координат и построенный на ее использовании оптический способ измерений размеров и положения объекта, и дальномер пеленгатор, который обеспечивает такую точность определения направления на объект наблюдения, его размеров и пространственного положения.

Дальномер-пеленгатор имеет неоспоримые преимущества перед используемыми дальномерными оптическими средствами наблюдения за космическими объектами, так как его увеличение и разрешающую способность можно обеспечить на порядки больше всех существующих оптических средств.

Предлагаемое техническое решение имеет изобретательский уровень, поскольку из опубликованных научных данных и известных технических решений явным образом не следует, что заявленная последовательность операций и устройство для его осуществления повышает точность измерения расстояний и размеров объекта.

Предлагаемое техническое решение промышленно применимо, так как для его реализации могут быть использованы стандартные устройства, оборудование и приспособления, используемые для оптических измерений.

Технико-экономическая эффективность заявленного способа и устройства заключается в возможности измерения размеров объектов и их положения достоверно с оценкой относительной погрешности.

Использованная литература

1. Физический энциклопедический словарь. - М.: Научное издательство "Советская энциклопедия". - 1983. - 928 с.

2. Гузевич С.Н. Патент №2468336 C1 (№2011120664/28 от 20.05.2011 г.). Стереоскопический способ измерения расстояний и судовой дальномер-пеленгатор. Опубликовано 27.11.2012. Бюл. №33.

3. Гузевич С.Н. Парная проективная геометрия на постулатах Евклида. Издательство: - LAP LAMBERT Academic Publishing GmbH & Co. KG, 2012 - 124 c.

1. Оптический способ измерений объекта и его положения, включающий выполнение измерений в парной проективной системе координат - наведение оси наблюдений на объект, получение отображений объекта на плоскости измерений, ортогональной осям двух идентичных оптических устройств, разнесенных на известной базе, управление размером базы и расстоянием от центров оптических устройств до плоскостей измерений, измерение положений граничных точек отображений объекта на осях координат и вычисление расстояния до объекта и его размеров, используя как опорную меру измерений расстояние от центров оптических устройств до измерительных плоскостей, отличающийся тем, что с целью повышения точности определения размеров объекта и его положения дополнительно выполняют измерения его отображений в дополнительной зеркальной парной проективной системе координат.

2. Способ по п.1, отличающийся тем, что с целью повышения разрешающей способности измерений, разбивают проекции отображения объекта, полученные на осях зеркальной системы координат, опорной мерой, равной расстоянию от центра проектирования до плоскости измерений, максимальное число делений транслируют на все другие проекции путем проведения через точки деления прямых, параллельных гипотенузам, соединяющим концы полученных проекций на ортогональных осях зеркальной системы координат, в том числе и на опорную меру измерений, получая новую опорную меру, вычисляют индивидуальные меры измерений для каждой из проекций, повторяют процесс разделения проекций отображений вновь полученной мерой до получения требуемой разрешающей способности измеряемых размеров объекта, а требуемые размеры объекта и его положения определяют произведением индивидуальной меры измерений каждой проекции на транслируемое число делений.

3. Дальномер-пеленгатор для реализации стереоскопического способа по п.1, состоящий из двух параллельных оптических устройств, жестко установленных на базе, двух измерительных плоскостей, механизма поворота базы по двум осям, устройств управления изменением размеров базы и отстояния измерительной плоскости от центров оптических устройств, систем переноса отображений на плоскости измерений, блока управления и блока вычислений, блок управления подключен к механизмам поворота базы по двум осям и устройствам изменения длины базы и отстояния измерительных плоскостей от центров оптических устройств, а измерительные плоскости в виде матриц установлены на общей плоскости, параллельной базе, выходы которых подключены к блоку вычислений, отличающийся тем, что дополнительно установлены две параллельные матричные измерительные плоскости на той же базе, ортогональные первым, чувствительные поверхности которых обращены друг к другу, выход которых подключен к блоку вычислений.