Способ формирования изображения с субдифракционным разрешением

Способ формирования изображения с субдифракционным разрешением

Иллюстрации

Показать все

Реферат

Изобретение относится к способам и устройствам радиовидения, радиолокации и радиоастрономии (далее все вместе - устройства радиовидения) миллиметрового, терагерцевого и дальнего инфракрасного диапазонов электромагнитного излучения и может быть использовано для построения радиоизображений различных объектов, являющихся источниками первичного и/или вторичного излучения радиоволн указанных диапазонов.

Устройства радиовидения используются для получения изображений различных объектов искусственного и естественного происхождения, являющихся источниками электромагнитного излучения. Такое устройство включает в себя оптическую систему, осуществляющую пространственное преобразование поля излучения источников. Типовым вариантом построения оптической системы является система, имеющая две фокальные плоскости. Идеальная оптическая система такого типа преобразует поле источников излучения, расположенных в одной фокальной плоскости, в электромагнитное поле (поле изображения) в другой фокальной плоскости. При этом преобразованное поле идентично исходному полю с точностью до линейного смещения и масштабирующего множителя, задающего сжатие или растяжение исходного поля. В неидеальной оптической системе существуют оптические искажения изображения (аберрации) и помехи шумовой и другой природы. Предлагаемый способ формирования изображения предназначен для избавления преобразованного поля от искажений и помех в неидеальной оптической системе и формирования (построения) соответствующего изображения, насколько возможно близкого к идеальному.

Принято плоскость, в которой расположены источники излучения, называть плоскостью источников изображения. Реконструированное изображение формируется в этой плоскости. Точки в плоскости источников изображения описываются в системе координат х0у.

Вторую фокальную плоскость оптической системы, в которой создается преобразованное поле, называют просто фокальной плоскостью оптической системы. Она может быть единственной фокальной плоскостью в том случае, когда плоскость источников удалена на достаточно большое расстояние от оптической системы, которое можно считать бесконечным. Такая ситуация характерна для устройств радиоастрономии. Точки в фокальной плоскости оптической системы описываются в системе координат ξ0η.

В качестве оптической системы могут использоваться зеркальные антенны. Известна оптическая система в виде двухзеркальной антенны Кассегрена (Сазонов Д.М. Антенны и устройства СВЧ. М.: Высшая школа. 1988). Она может быть сфокусирована как на конечном, так и на бесконечном расстоянии до источника излучения.

Известны оптические системы на основе диэлектрических линз (Зелкин Е.Г., Петрова Р.А. Линзовые антенны. М.: Советское радио, 1974). Для построения оптических систем используются также более сложные линзы, например, линза Ротмана и линза Люнеберга (Корнблит С., СВЧ оптика, М.: «Связь», 1980).

Известны стационарные и сканирующие оптические системы.

Заявляемое изобретение относится к сканирующим оптическим системам. В них имеется возможность перемещения поля в фокальной плоскости. Такое перемещение достигается разными способами. Наиболее простым из них является перемещение всей оптической системы. В радиоастрономии при исследовании удаленных объектов используется частный вид перемещения оптической системы - ее вращение. Достоинством сканирования путем механического перемещения оптической системы является отсутствие дополнительных искажений - аберраций, связанных с процессом сканирования.

Известна сканирующая оптическая система на основе двухзеркальной антенны Кассегрена, в которой сканирование достигается за счет перемещения вспомогательного зеркала - субрефлектора (May Т., Zieger G., Anders S., Zakosarenko V.M., Meyer H.-G., Thorwirth G., Kreysa E., Passive stand-off Terahertz imaging with 1 Hertz frame rate // Proc. SPIE, Vol.6949, 6949C (2008); DOI: 10.1117/12.777952). Перемещение субрефлектора, имеющего массу, существенно меньшую массы всей оптической системы, реализуется намного проще. Поэтому скорость сканирования в данном случае много больше, чем при перемещении всей оптической системы. Однако, перемещение субрефлектора приводит к появлению дополнительных аберраций оптической системы.

Выше отмечалось, что идеальная оптическая система преобразует поле в плоскости источников изображения в поле в фокальной плоскости, осуществляя с ним две операции: перемещение и масштабирование. Как правило, оптические системы строятся так, что в них осуществляется сжатие поля. Математически преобразование поля источников с интенсивностью U(x, у) в поле в фокальной плоскости U_f(ξ, η) описывается для идеальной оптической системы следующим образом:

U f ( ξ ,   η ) = A ∫ S U ( x ,   y ) δ ( α ( ξ − ξ ' ) − x ) δ ( α ( η − η ' ) − y ) d x d y ,   ( 1 )

где А - амплитудный множитель, α - коэффициент масштабирования поля, ξ', η' - параметры, задающие сдвиг поля, δ(x) - дельта функция, S - участок плоскости источников, в котором находятся источники изображения.

Функция K_OS(x, y, ξ, η), имеющая вид

K O S ( x ,   y ,   ξ ,   η ) = δ ( α ( ξ − ξ ' ) − x ) δ ( α ( η − η ' ) − y ) ,   ( 2 )

под интегралом в (1) называется аппаратной функцией оптической системы. Для конкретной реальной оптической системы она описывается более сложным образом, который позволяет учитывать существующие в ней аберрации.

Аберрации имеют разную физическую природу и по-разному влияют на вид аппаратной функции оптической системы. Известны геометрооптические аберрации: астигматизм, кома и т.д. Они связаны с тем, что оптическая система осуществляет фокусировку поля неидеально. Аберрации этого типа не носят принципиального характера. Они могут быть уменьшены путем улучшения оптической системы. В качестве путей улучшения можно указать увеличение точек идеальной фокусировки, то есть переход к полифокальным системам. Идеальной безаберрационной оптической системой, например, является упомянутая выше линза Люнеберга, представляющая собой сферу с переменной по радиусу диэлектрической проницаемостью.

Имеются также аберрации, связанные с волновой природой электромагнитного поля. Они носят принципиальный характер, поскольку устранить их путем улучшения конструкции оптической системы невозможно. Влияние таких аберраций на аппаратную функцию оптической системы K_OS(x, y, ξ, η) выражается в том, что даже в отсутствие геометрооптических аберраций она не может быть представлена в виде произведения дельта функций. Типичная аппаратная функция оптической системы без геометрооптических аберраций имеет следующий вид:

K O S ( x ,   y ,   ξ ,   η ) = J 1 ( b r ( x ,   y ,   ξ ,   η ) ) r ( x ,   y ,   ξ ,   η ) ,   ( 3 ) r ( x ,   y ,   ξ ,   η ) = ( ( ξ − ξ ' ) − x / α ) 2 + ( ( η − η ' ) − y / α ) 2 ,

где b - параметр, определяемый оптической системой, J₁(x) - функция Бесселя первого порядка. Параметр b=πD/λF обратно пропорционален длине волны λ.

Из выражений (2) и (3) видно, что любой точечный источник изображения, независимый или входящий в состав источников изображения, находящийся в плоскости источников изображения, превращается в фокальной плоскости в «пятно», ширина которого задается параметром b и свойствами оптической системы. Искажения такого типа получили название дифракционных искажений, а пятно, названное выше, получило название пятна Эйри (Сивухин Д.В., Общий курс физики, том IV, Оптика, Москва, Наука, 1985). Диаметр пятна Эйри h определяется так называемым критерием Рэлея, который устанавливает предел концентрации (фокусировки) электромагнитного поля с помощью оптических систем:

h = 2,44 λ D ⋅ F ,   ( 4 )

где λ - длина волны излучения, D - диаметр первичного зеркала или линзы оптической системы, F - фокусное расстояние оптической системы. Для однозеркальной или однолинзовой системы эквивалентное фокусное расстояние равно фокусному расстоянию зеркала или линзы. Для более сложных многоэлементных систем оно может быть определено по известным соотношениям.

Диаметр пятна Эйри h является важным параметром оптической системы, который определяет ее собственную разрешающую способность в фокальной плоскости. Он показывает минимальное расстояние между полем точечных источников в фокальной плоскости, которое способна зарегистрировать данная оптическая система. Важно отметить, что в силу того, что оптическая система осуществляет масштабирующее преобразование поля в плоскости источников излучения к полю изображения в фокальной плоскости, то для определения минимального расстояния различимых точечных источников в плоскости источников ρ использовать параметр h непосредственно невозможно, поскольку указанное расстояние связано с ним следующим образом:

h=kρ,

где k - коэффициент сжатия поля, который обычно меньше единицы. При k>1 правильнее говорить о растяжении поля в фокальной плоскости.

Параметр ρ определяет собственную разрешающую способность оптической системы в плоскости источников.

Другим важным элементом системы радиовидения является матричный приемник. Матричный приемник представляет собой решетку приемных элементов, которые преобразуют энергию падающего на них электромагнитного поля изображения в электрические сигналы. Приемные элементы располагаются в фокальной плоскости оптической системы. Типичным является размещение приемных элементов периодически в узлах прямоугольной или гексагональной сеток.

Матричный приемник содержит М элементов, каждый из которых описывается своим номером m, 1≤m≤М. Электрический сигнал на выходе m-го приемного элемента p_m связан с полем в фокальной плоскости следующим образом:

p m = ∫ S U ( x ,   y ) K m ( x ,   y ) d x d y ,   ( 5 )

где

K m ( x ,   y ) = A ∫ S m F ( ξ ,   η ) K O S ( x ,   y ,   ξ ,   η ) d ξ d η ,

F(ξ, η) - известная весовая функция, которая определяется структурой приемного элемента, S_m - область в фокальной плоскости, в которой функция F(ξ, η) отлична от нуля, и А - амплитудный множитель.

Функции K_m(х, у,) называются аппаратными функциями оптической

системы вместе с матричным приемником. Аппаратная функция сканирующей оптической системы в общем случае меняется в процессе сканирования. Для их описания используют функции с индексом K_OS,n(x, y, ξ, η), которые являются аппаратными функциями оптической системы на каждом шаге сканирования. Соответственно для сканирующей оптической системы вместе с матричным приемником электрические сигналы и аппаратные функции также имеют два индекса: p_n,m и K_n,m(x, y,).

Аппаратная функция комплекса "оптическая система плюс матричный приемник" является важнейшей характеристикой системы радиовидения. Она может быть рассчитана, а в практическом случае может быть получена в результате ее прямого измерения с помощью независимого точечного источника излучения с характеристикой U(x, y)=Сδ(x-x₀)δ(у-у₀), где С - интенсивность излучаемого этим источником сигнала, при пошаговом перемещении этого точечного источника в плоскости источников изображения и формирования массива значений соответствующих электрических сигналов на выходах матричного приемника. Из приведенных выше соотношений видно, что в этом случае сигналы p_n,m совпадают с искомыми аппаратными функциями. Чтобы отличать их от электрических сигналов, получаемых при измерении излучения от изображения, обозначим их q_n,m. Далее эта процедура рассмотрена более подробно.

Известны разные способы получения изображения источников излучения с помощью сканирующей оптической системы. Они основаны на преобразовании указанного поля излучения на каждом шаге сканирования в электрические сигналы на выходах матричного приемника, который расположен в фокальной плоскости оптической системы, и формирования массива значений указанных электрических сигналов p_n,m, 1≤n≤N, 1≤m≤М, N - общее число шагов перемещения поля излучения в ходе цикла сканирования, М - общее число элементов матричного приемника.

Известен наиболее простой способ получения изображения (Heinz E., May Т., Zieger G., Born D., Anders S., Thorwirth G., Zakosarenko V.М., Schubert М., Krause Т., Starkloff М., Kriiger A., Schulz М., Bauer F., Meyer H.-G., Passive Submillimeter-wave Stand-off Video Camera for Security Applications, J. Infrared Milli Terahz Waves, DOI 10.1007/s10762-010-9716-y, 28 Sept. 2010). Этот способ построения изображения основан на использовании функций отображения x(ξ, η), y(ξ, η). Функции отображения определяются в ходе калибровки системы радиовидения. Для каждого положения приемного элемента в фокальной плоскости, характеризуемого координатами ξ, η, может быть найден максимум аппаратной функции, который находится на плоскости источников в точке с координатами x, у. Функции отображения связывают координаты точек на плоскости источников с координатами точек в фокальной плоскости.

В рамках названного способа формируется массив значений

интенсивности изображения u_n,m следующим образом:

u n , m = p n , m ,   ( 6 )

где p_n,m - сформированный массив электрических сигналов, которые получены с выходов приемных элементов, расположенных в точках ξ_n,m, η_n,m. С помощью функций отображения находятся координаты точек x_n,m, y_n,m на плоскости источников, которые соответствуют массиву значений интенсивности изображения u_n,m. Массив дискретных значений интенсивности изображения несет достаточную информацию для построения методами аппроксимации непрерывной функции U(x, y), описывающей интенсивность изображения в некоторой области на плоскости источников.

Недостатком такого способа построения изображения является его низкая разрешающая способность. Непосредственное использование массива электрических сигналов p_n,m для формирования массива значений интенсивности изображения u_n,m не позволяет устранить влияние дифракционных искажений, связанных с конечными размерами пятна Эйри. В результате изображение оказывается «размытым». Оно не способно передать быстрых изменений распределения интенсивности источников излучения, расположенных в плоскости источников.

Наиболее близкий способ построения изображения к заявляемому описан в патенте РФ (Выставкин А.Н., Пестряков А.В., Банков С.Е., Чеботарев В.М., Патент РФ на изобретение №2398253 «Устройство формирования изображения с субдифракционным разрешением», приоритет от 18 марта 2009 г.). В этом известном способе изображение источников излучения в диапазонах миллиметровых, терагерцевых и дальних инфракрасных волн, расположенных в плоскости источников, формируется с помощью оптической системы, выполненной с возможностью пошагового перемещения поля излучения, которое создается источниками излучения в фокальной плоскости оптической системы, путем преобразования указанного поля излучения на каждом шаге перемещения в электрические сигналы на выходах матричного приемника, который расположен в фокальной плоскости оптической системы, и последующего формирования массива значений указанных электрических сигналов p_n,m. Поле излучения в фокальной плоскости оптической системы в известном способе построения изображения перемещается по окружности, то есть совершает круговое перемещение. При этом, центр этого перемещения смещен относительно центра матричного приемника. В плоскости источников вводится прямоугольная сетка с узлами в точках с координатами x_i и y_j, 1≤i≤N_x, 1≤j≤N_y, где N_x - число ячеек прямоугольной сетки по оси 0х, а N_y - число ячеек прямоугольной сетки по оси 0у. Далее формируется двумерный массив u_i,j значений интенсивности изображения в узлах прямоугольной сетки, двумерный массив u_i,j определяется из условия минимизации функционала L(u):

L ( u ) = ∑ n = 1 N ∑ m = 1 M | p n , m − ∫ S U ( x ,   y ) K n , m ( x ,   y ) d x d y | 2 +   ( 7 ) + α ∫ S | U ( x ,   y ) | 2 d x d y ,

где

U(x, y)=u_i,j

x_i≤x≤x_i+1; y_i≤y≤y_i+1

и S - область, в которой строится изображение, α - малый параметр.

Такой способ построения изображения позволяет получать изображения с разрешающей способностью, превышающей ограничение, устанавливаемое критерием Рэлея.

Недостатком данного способа построения изображения является его неустойчивость по отношению к шумам и помехам других видов. Моделирование практического применения этого способа построения изображения (Bankov S.Е., Chebotarev V.М., Cherepenin V.A., Korjenevsky А.V., Pestryakov А.V., Vystavkin A.N., Image production with sub-diffraction resolution in radio vision devices of the terahertz range using receiving arrays and image scanning procedure, Vestnik Novosibirsk State University, Series: Physics, 2010, Volume 5, issue 4) показало, что формирование изображения с его помощью возможно при отношении сигнал/шум на выходах матричного приемника не меньшем 50. Под сигналом на выходе матричного приемника при определении отношения сигнал/шум понимается сигнал, который получается при настройке аппаратной функции оптической системы вместе с матричным приемником на максимум. Под шумом понимается собственный шум матричного приемника.

Аналогичная картина имеет место и для других случаев применения названного метода с применением процедуры минимизации функционала (7).

Предлагаемое решение нацелено на получение технического результата, выражающегося в повышении разрешающей способности изображения при наличии оптических, конкретно дифракционных искажений, а также шумов и других помех. Получаемый результат выражается в построении в диапазонах миллиметровых, терагерцевых и дальних инфракрасных волн изображений источников излучения с четкостью, превышающей критерий Рэлея для оптической системы с заданными размерами при наличии помех разной природы. Достижение указанного технического результата позволяет снизить стоимость систем радиовидения за счет уменьшения размеров оптической системы при фиксированном уровне разрешающей способности изображения или повысить разрешающую способность при заданных размерах оптической системы.

Предлагаемый способ формирования изображения, создаваемого источниками излучения, которые излучают в диапазонах миллиметровых, терагерцевых и дальних инфракрасных волн и расположены в плоскости источников, с помощью оптической системы, выполненной с возможностью пошагового перемещения поля излучения, которое создается источниками излучения в фокальной плоскости оптической системы, путем преобразования указанного поля излучения на каждом шаге перемещения в электрические сигналы на выходах матричного приемника, который расположен в фокальной плоскости оптической системы, и последующего формирования массива значений указанных электрических сигналов p_n,m, 1≤n≤N, 1≤m≤М, где p_n,m - величина электрического сигнала на n-м шаге перемещения поля излучения на m-м выходе матричного приемника, N - общее число шагов перемещения поля излучения, М - общее число элементов матричного приемника, решает задачу формирования изображения с повышенным разрешением при наличии дифракционных искажений, а также шумов и других помех в оптической системе и окружающей среде.

Эта задача решается за счет того, что в плоскости источников вводится прямоугольная сетка с узлами в точках с координатами x_i и y_i, 1≤i≤N_x, 1≤j≤N_y, где N_x - число ячеек прямоугольной сетки по оси 0х, а N_y - число ячеек прямоугольной сетки по оси 0у, в узлах прямоугольной сетки последовательно размещается независимый точечный источник, осуществляется пошаговое перемещение поля излучения точечного источника и формируется массив значений электрических сигналов на выходах матричного приемника q_n,m,I,j, на каждом шаге перемещения поля излучения точечного источника для каждого положения точечного источника в узлах прямоугольной сетки формируется двумерный массив u_i,j значений интенсивности изображения в узлах прямоугольной сетки, причем двумерный массив u_i,j формируется из условия минимизации вариации интенсивности изображения L(u):

L ( u ) = ∑ i = 1 N x ∑ j − 1 N y − 1 | u i , j + 1 − u i , j | + ∑ i = 1 N x − 1 ∑ j − 1 N y | u i + 1, j − u i , j |   ( 8 )

при ограничениях

max 1 ≤ n ≤ N 1 ≤ m ≤ M | p n , m − ∑ i = 1 N x − 1 ∑ j = 1 N y − 1 u i , j q n , m , i , j Δ x i Δ y j | ≤ δ } ,   ( 9 ) u i , j ≥ 0,

где Δx_j=x_j+1-X_j, Δy_j=y_j+1-y_j, δ - заданная погрешность формирования массива значений интенсивности изображения в узлах прямоугольной сетки, размерность массива величин электрических сигналов на выходах матричного приемника NM выбирается большей числа узлов прямоугольной сетки N_xN_y. Это обеспечивает избыточность данных над числом переменных в задаче, что необходимо для получения ее решения.

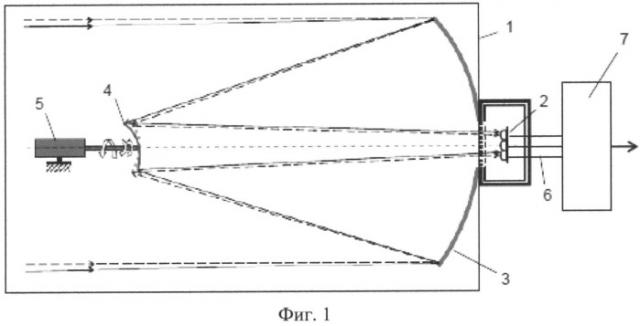
На фиг.1 показан один из возможных вариантов выполнения устройства, реализующего предлагаемый способ формирования изображения. Устройство содержит оптическую систему 1 и матричный приемник 2. Оптическая система 1 выполнена в виде двухзеркального телескопа по схеме Кассегрена. Она содержит главное зеркало 3 и субрефлектор 4. Субрефлектор 4 выполнен с возможностью перемещения, а конкретно, с возможностью вращения и изменения угла наклона относительно оси главного зеркала 3. Возможность вращения и изменения угла наклона обеспечивается комплектом из двух двигателей 5. Матричный приемник расположен в фокальной плоскости оптической системы 1.

Следует заметить, что возможны близкие варианты выполнения устройства, реализующего предлагаемый способ формирования изображения, например, с установкой на выходе оптической системы вращающегося К-зеркала, или другого подвижного зеркала или системы подвижных зеркал, осуществляющих пошаговое перемещение поля излучения в оптической системе. Описываемый способ формирования изображения с субдифракционным разрешением может быть реализован и с их помощью. Дальнейшее описание способа формирования изображения с субдифракционным разрешением проводится на примере оптической системы с двухзеркальной антенной Кассегрена.

Сигналы p_n,m и q_n,m,I,j с выходов 6 матричного приемника 2 поступают в устройство запоминания массивов значений электрических сигналов 7, которое может быть выполнено в виде регистра памяти. Сформированные массивы значений электрических сигналов могут быть переданы с выхода устройства запоминания массивов значений электрических сигналов 7 на внешнее устройство для дальнейшего их использования при осуществлении способа формирования изображения.

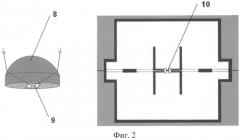
На фиг.2 показан в качестве одного из вариантов элемент матричного приемника 2, который выполнен в виде иммерсионной линзы 8, которая объединена с подложкой. Подложка служит металлическим экраном, в котором выполнена двухщелевая антенна 9. На противоположной стороне подложки размещается проводник микрополосковой линии. В разрыв указанного проводника включен приемный элемент 10, который может быть выполнен, например, в виде сверхпроводникового болометра. Сверхпроводниковые болометры имеют низкий уровень собственных шумов и применяются в приемниках терагерцевого излучения. Низкочастотный сигнал с выхода сверхпроводникового болометра поступает в микрополосковую линию, которая используется в качестве выхода 6 матричного приемника 2.

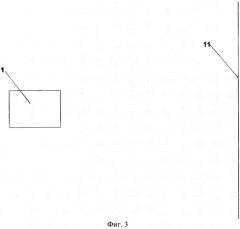
На фиг.3 показано размещение оптической системы 1 относительно плоскости источников 11. Источники излучения имеют различную природу. Это могут быть реальные источники излучения в виде излучателей, на которые подается мощность от генератора. Также источниками излучения могут служить отражающие объекты, которые рассеивают излучение от внешних источников, расположенных вне плоскости источников 11. Возможно также появление виртуальных источников, например, в виде излучения, проходящего через плоскость источников 11.

Независимо от типа источника задачей устройства, реализующего способ формирования изображения, является построение изображения источников, расположенных в плоскости источников 11.

Плоскость источников 11 может находиться на конечном расстоянии от оптической системы 1. В этом случае оптическая система 1 должна быть сфокусирована на плоскость источников 11. В радиоастрономии плоскость источников 11 расположена на расстоянии, которое многократно превышает размеры оптической системы 1. Такое расстояние можно считать бесконечно большим. В этом случае оптическая система должна быть сфокусирована на бесконечность. Фокусировка на разные расстояния достигается выбором формы главного зеркала 3. При конечном расстоянии оно имеет эллиптическую форму, а при бесконечном - параболическую.

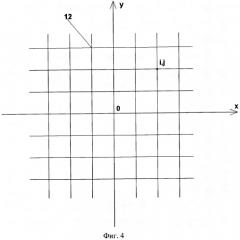
Для формирования (построения) изображения, как указывалось выше, в плоскости источников 11 вводится прямоугольная сетка 12, как показано на фиг.4. Узлы прямоугольной сетки 12 характеризуются индексами i, j, которые изменяются в пределах:

1 ≤ i ≤ N x ,   ( 10 ) 1 ≤ j ≤ N y ,

где N_x и N_y - числа узлов прямоугольной сетки 12 по осям 0х и 0у, соответственно. Общее число узлов прямоугольной сетки 12 равно N_xN_y. Прямоугольная сетка 12 может быть выполнена с постоянным шагом, как показано на фиг.4. Она также может иметь переменный шаг Δx_j=x_j+1-x_i по оси 0x или Δy_j=y_j+1-y_j по оси 0у.

Размерность массива величин электрических сигналов на выходах матричного приемника NM выбирается большей числа узлов прямоугольной сетки N_xN_y, о чем говорилось выше. Это неравенство определяет параметры перемещения поля излучения, которое создается источниками излучения в фокальной плоскости оптической системы 1.

Рассмотрим детально формирование изображения в соответствии с предлагаемым способом. Изображение формируется в несколько этапов. На первом этапе оптическая система 1 и матричный приемник 2 принимают сигналы от источников излучения, которые назовем исследуемыми источниками излучения. Изображение исследуемых источников должно быть сформировано в соответствии с предлагаемым способом.

Излучение исследуемых источников преобразуется оптической системой 1 в поле излучения в фокальной плоскости оптической системы 1. Оптическая система 1 выполнена с возможностью пошагового перемещения поля излучения в фокальной плоскости. Цикл перемещения поля излучения в фокальной плоскости или цикл сканирования включает N шагов. Каждый шаг сканирования описывается номером n, 1≤n≤N. Матричный приемник 2 на каждом шаге перемещения поля излучения в фокальной плоскости оптической системы 1 преобразует поле излучения в фокальной плоскости оптической системы в электрические сигналы p_n,m, 1≤m≤М, на выходах 6 матричного приемника 2. Здесь m - номер выхода 6 матричного приемника 2, а М - общее число выходов 6 матричного приемника 2. Множество электрических сигналов p_n,m образует массив значений электрических сигналов p, который с выходов 6 поступает в устройство запоминания массива значений электрических сигналов 7.

Процесс сканирования поясняется на фиг.5, на которой отображено пошаговое перемещение поля излучения, т.е. изображения в фокальной плоскости оптической системы 1, показанной на фиг.1. Оптическая система 1 в рассматриваемом примере сфокусирована на бесконечность и принимает поле излучения, которое создается спиральной галактикой M101. На фиг.5 белыми кружками условно показаны семь приемных элементов матричного приемника 2. Поле излучения в фокальной плоскости совершает круговое перемещение относительно неподвижного матричного приемника. При этом, центр изображения смещен относительно центра матричного приемника. На фиг.5 представлено четыре кадра, отображающих круговое перемещение для числа шагов N=4. В реальной процедуре сканирования их намного больше с тем, чтобы обеспечить условие NM>>N_xN_y, о котором говорилось выше и которое необходимо для получения решения задачи.

На втором этапе в плоскость источников 11 помещается независимый точечный источник большой интенсивности, излучающий в том же диапазоне радиоволн, что и исследуемые источники излучения. Под большой интенсивностью понимается такой уровень излучаемой мощности, который обеспечивает на каждом выходе 6 матричного приемника 2 в положении, соответствующем максимуму аппаратной функции, отношение сигнал/шум много большее единицы. В этом случае влияние шумов оказывается несущественным. Точечный источник имеет геометрические размеры, много меньшие длины волны в свободном пространстве. В качестве такого источника может использоваться, например, излучающий электрический диполь.

Точечный источник последовательно помещается во все узлы прямоугольной сетки 12 с индексами i,j. Для каждого положения точечного источника осуществляется пошаговое круговое перемещение поля излучения в фокальной плоскости оптической системы 1 по той же стратегии, что и перемещение изображения на фиг.5. Одновременно с выходов 6 матричного приемника 2 снимаются электрические сигналы q_n,m,I,j, которые поступают в устройство запоминания массивов электрических сигналов 7. Таким образом, формируется массив значений электрических сигналов q. Массивы

значений электрических сигналов p и q используются на следующих этапах формирования изображения.

Изображение, подлежащее формированию, описывается функцией U(x, y), которая определена в плоскости источников 11. Эта функция пропорциональна интенсивности (мощности) источника в задаваемой точке с координатами x, у на плоскости источников 11. В соответствии с предлагаемым способом формирования изображения последнее представляет собой массив значений интенсивности изображения u_i,j, в узлах прямоугольной сетки 12. Зная интенсивность изображения в дискретных точках, мы можем, если потребуется, найти ее значение в произвольной точке на плоскости источников 11, используя процедуру аппроксимации. Хорошо известный способ линейной аппроксимации позволяет записать интенсивность изображения в виде билинейной функции:

U ( x ,   y ) = 1 Δ x i Δ y j ( ( x − x i + 1 ) ( y − y j + 1 ) u i , j − ( x − x i + 1 ) ( y − y j ) u i , j + 1 − − ( x − x i ) ( y − y j + 1 ) u i + 1, j − ( x − x i )