Способ определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров

Способ определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой обработки сигналов и может быть использовано для определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров для неразрушающего контроля и диагностики оборудования на основе корреляционного анализа.

Известен способ определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров, используемый при решении задач обнаружения утечек в трубопроводах, выбранный в качестве прототипа [А.Л. Овчинников, Б.М. Лапшин, А.С. Чекалин, А.С. Евсиков. Опыт применения течеискателя ТАК-2005 в городском трубопроводном хозяйстве //Известия Томского политехнического университета. - 2008. -Т. 312. - №2. - С. 196-202], заключающийся в измерении и дискретизации двух аналоговых сигналов, поступающих с датчиков, и расчете функции когерентности этих сигналов, по которой находят частотные границы полезного сигнала, в которых анализируемые сигналы когерентны, т.е. значения функции когерентности принимают единичные и/или ярко выраженные максимальные значения. По найденным диапазонам задают границы полос пропускания цифровых частотных фильтров.

Этот способ имеет существенный недостаток. При наличии в анализируемых сигналах широкополосного шума и низкого отношения сигнал/шум исследуемые сигналы могут быть когерентны практически во всем частотном диапазоне.

Задачей изобретения является определение частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров.

Это достигается тем, что в способе определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров, так же как в прототипе осуществляют измерение и дискретизацию двух аналоговых сигналов.

Согласно изобретению производят прямое преобразования Фурье в форме быстрого преобразования Фурье входных дискретизированных сигналов размерностью 2 n , определяют комплексно-сопряженные значения результатов прямого преобразования одного из сигналов, попарно умножают полученные комплексные сигналы прямого преобразования Фурье с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала, из полученного произведения P j выбирают значения и формируют m сигналов M k ,

где j = 0,   1,   ...   ,   2 n − 1 + 1 ;

m = 2,   3,   ...,   2 n − 1 + 1 ;

k = 0,   1   ,   …   ,   m − 1 ,

согласно выражению

M j k = { P j , k m < j 2 n − 1 + 1 ≤ k + 1 m , 0,   и н а ч е . (1)

Полученные сигналы M k подвергают обратному преобразованию Фурье

Z k = F − 1 [ M k ] ,

По результатам обратного преобразования Фурье определяют взаимную частотно-временную корреляционную функцию

r 12 ( f k , t i ) = Z i k ,(2)

где t i ∈ [ t min ,   t max ]   ;

f k ∈ [ f min ,   f max ] ; t i = i ⋅ 1 f d ; f k = k ⋅ f max m − 1 ; t min = − 2 n − 1 f d ; t max = 2 n − 1 − 1 f d ; f min = f d 2 n ; f max = f d 2 ;

f d - частота дискретизации сигнала.

По полученным результатам строят график взаимной частотно-временной корреляционной функции r 12 ( f , t ) , по которому судят о наличии полезного сигнала и его частотных границах. По найденным границам полезного сигнала определяют границы полос пропускания цифровых частотных фильтров.

Взаимная частотно-временная корреляционная функция в предложенном способе позволяет определять наличие полезного сигнала и его частотные границы для настройки границ полос пропускания цифровых частотных фильтров. При этом использование быстрого преобразования Фурье обеспечивает высокое быстродействие и универсальность способа.

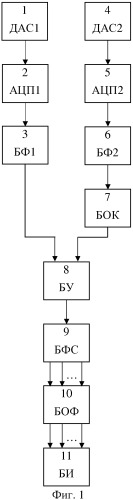
На фиг. 1 приведена аппаратная схема устройства, реализующего рассматриваемый способ определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров.

В таблице 1 приведены исходные данные и результаты анализа тестового примера.

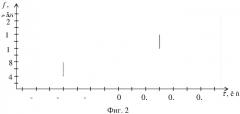
На фиг. 2 приведен график взаимной частотно-временной корреляционной функции результата анализа тестового примера.

Способ определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров может быть осуществлен с помощью устройства (фиг. 1), содержащего первый датчик для получения анализируемого сигнала 1 (ДАС1), подключенный к первому блоку аналого-цифрового преобразования 2 (АЦП1), выход которого соединен с входом первого блока прямого преобразования Фурье 3 (БФ1), второй датчик анализируемого сигнала 4 (ДАС2), к которому последовательно подключены второй блок аналого-цифрового преобразования 5 (АЦП2), второй блок прямого преобразования Фурье 6 (БФ2) и блок определения комплексно-сопряженного значения 7 (БОК). Выходы первого блока прямого преобразования Фурье 3 (БФ1) и блока определения комплексно-сопряженного значения 7 (БОК) соединены с входом блока умножения 8 (БУ), к которому последовательно подключены блок формирования сигналов 9 (БФС), блок обратного преобразования Фурье 10 (БОФ) и блок интерпретации 11 (БИ).

В качестве датчиков анализируемого сигнала 1 (ДАС1) и 4 (ДАС2) могут быть использованы датчики тока, например, промышленные приборы КЭИ-0.1 или датчики напряжения - трансформаторы напряжения (220/5 В). Блоки аналого-цифрового преобразования 2 (АЦП1) и 5 (АЦП2) могут быть реализованы на основе аналого-цифровых преобразователей ADS7827. Блоки прямого преобразования Фурье 3 (БФ1) и 6 (БФ2), блок определения комплексно-сопряженного значения 7 (БОК), блок умножения 8 (БУ), блок формирования сигналов 9 (БФС), блок обратного преобразования Фурье 10 (БОФ), блок интерпретации 11 (БИ) могут быть выполнены на микроконтроллере серии AVR32 производителя Аtmel AT32AP7000.

С выхода датчиков 1 (ДАС1) и 4 (ДАС2) анализируемые сложные сигналы, например,

y 1 ( t ) = y 2 ( t ) = u ( t ) ,

где u ( t ) - многочастотный сигнал напряжения (таблица 1),

поступают на входы аналого-цифровых преобразователей 2 (АЦП1) и 5 (АЦП2), с выхода которых дискретизированные сигналы

y 1 ( t i ) = y 2 ( t i ) = u ( t i ) ,

где t i = Δ t ⋅ i ,

i = 1,   2,   … ,   N ,

где N = 2 n = 2 15 = 32768 - размер выборки для быстрого преобразования Фурье;

Δ t = 1 44100 - шаг дискретизации сигнала u ( t i ) ,

поступают на входы блоков прямого преобразования Фурье (в форме БПФ) 3 (БФ1) и 6 (БФ2), где выполняют прямое преобразование Фурье входных сигналов. С выхода блока прямого преобразования Фурье 6 (БФ2) результаты прямого преобразования Фурье в виде комплексного сигнала размерностью 2 n − 1 + 1 = 1638 5 поступают на вход блока определения комплексно-сопряженного значения 7 (БОК), где определяют комплексно-сопряженные значения для каждого элемента сигнала. Результаты прямого преобразования Фурье БПФ 3 (БФ1) и блока определения комплексно-сопряженного значения 7 (БОК) поступают на вход блока умножения 8 (БУ), где выполняют попарное умножение двух комплексных сигналов. С выхода блока умножения 8 (БУ) результаты умножения в виде комплексного сигнала размерностью 2 n − 1 + 1 = 1638 5 поступают на вход блока формирования сигналов 9 (БФС), где формируют m = 421 комплексных сигналов размерностью 2 n − 1 + 1 = 1638 5 согласно выражению (1). С выхода блока формирования сигналов 9 (БФС) полученные комплексные сигналы поступают на вход блока вычисления обратного преобразования Фурье 10 (БОФ), где выполняют обратное преобразование Фурье над каждым комплексным сигналом. С выхода блока вычисления обратного преобразования Фурье 10 (БОФ) результаты обратного преобразования Фурье в виде действительных m = 421 сигналов размерностью

N = 2 n = 2 15 = 32768

поступают на вход блока интерпретации 11 (БИ), где согласно выражению (2) определяют взаимную частотно-временную корреляционную функцию. Для m = 421 и k = 76 , получили f k = f 76 = 3990 Гц,

при k = 153 получаем f k = f 153 = 8032 .5 Гц,

при k = 228 получили f k = f 228 = 11970 Гц,

при k = 305 получили f k = f 305 = 16012 .5 Гц.

Полученная взаимная частотно-временная корреляционная функция (фиг. 2) имеет две ярко выраженные вертикальные полосы на двух частотных диапазонах, граничные значения которых близки к заданным в тестовом примере. По найденным границам полезного сигнала задают границы полос пропускания цифровых частотных фильтров.

Способ определения частотных границ полезного сигнала и полос пропускания цифровых частотных фильтров, включающий измерение и дискретизацию двух аналоговых сигналов, отличающийся тем, что дискретизированные сигналы подвергают прямому преобразованию Фурье в форме быстрого преобразования Фурье размерностью 2 n , определяют комплексно-сопряженные значения результатов прямого преобразования одного из сигналов, попарно умножают полученные комплексные сигналы прямого преобразования Фурье с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала, из полученного произведения P j , результатов прямого преобразования Фурье первого сигнала с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала выбирают значения и формируют m сигналов M k ,где j = 0,   1,   ...   ,   2 n − 1 + 1 ; m = 2,   3,   ...,   2 n − 1 + 1 ; k = 0,   1   ,   …   ,   m − 1 ,согласно выражению M j k = { P j , k m < j 2 n − 1 + 1 ≤ k + 1 m , 0,   и н а ч е . полученные сигналы M k подвергают обратному преобразованию Фурье Z k = F − 1 [ M k ] ,определяют взаимную частотно-временную корреляционную функцию r 12 ( f k , t i ) = Z i k ,где t i ∈ [ t min ,   t max ]   ; f k ∈ [ f min ,   f max ] ; t i = i ⋅ 1 f d ; f k = k ⋅ f max m − 1 ; t min = − 2 n − 1 f d ; t max = 2 n − 1 − 1 f d ; f min = f d 2 n ; f max = f d 2 ; f d - частота дискретизации сигнала,далее по полученным результатам строят график взаимной частотно-временной корреляционной функции r 12 ( f , t ) , по которому судят о наличии полезного сигнала, его частотных границах, по которым определяют границы полос пропускания цифровых частотных фильтров.