Кодирование точек эллиптической кривой

Кодирование точек эллиптической кривой

Иллюстрации

Показать все

Реферат

Настоящее изобретение касается криптографической обработки сообщений, основанной на использовании точек эллиптической кривой, и, в частности, такой криптографии, которая носит детерминистический характер.

Для применения криптографического вычисления к сообщению традиционно используют алгоритмы включения произвольных значений в математические структуры. Для этого эллиптические кривые являются математическими структурами, которые облегчают применение таких криптографических вычислений и позволяют сэкономить объем памяти по сравнению с применением других криптографических вычислений.

Вместе с тем эффективные алгоритмы включения произвольных значений, использующие эллиптические кривые, являются вероятностными. Следовательно, время применения таких алгоритмов не является постоянным и зависит от кодируемого сообщения. Таким образом, если хакер определяет различные сроки применения используемого алгоритма, он может получить информацию о закодированном сообщении.

Чтобы скрыть время, используемое вероятностным алгоритмом включения, можно предусмотреть добавление бесполезных этапов в этот алгоритм, чтобы его применение всегда занимало период времени одинаковой длины при любом обрабатываемом сообщении.

Однако такая обработка является сложной и занимает много времени.

Настоящее изобретение призвано улучшить эту ситуацию.

В качестве первого объекта изобретением предлагается способ выполнения криптографического вычисления в электронном компоненте, содержащий этап получения точек Р на эллиптической кривой, удовлетворяющих следующему уравнению:

Y 2 + a 1 X Y + a 3 Y = X 3 + a 2 X 2 + a 4 + X + a 6               (1)

где а₁, а₂, а₃, а₄ и a₆ являются элементами множества А элементов,

где А является кольцом Z/qZ целых чисел по модулю q, где q является положительным целым числом, являющимся произведением числа I разных простых чисел, строго превышающих 3, при этом I является целым числом, превышающим или равным 2, или А является конечным полем F_q, где q является показателем степени простого целого числа;

где Х и Y являются координатами точек Р и являются элементами А,

при этом указанный способ содержит этапы, на которых:

/а/ определяют параметр (11);

/b/ получают координаты Х и Y точки Р (13) посредством применения к этому параметру некоторой функции (12);

при этом функция φ Эйлера для множества А удовлетворяет формуле:

φ(А)mod3=1,

причем указанная функция является обратимой и детерминистической функцией, выраженной рациональной дробью в a₁, а₂, а₃, а₄ и а₆ и в указанном параметре в А и достигающей, по меньшей мере, числа d/4^I точек Р при I, равном 1 для конечного поля F_q;

/с/ указанную точку Р используют для применения в криптографии для шифрования, или хеширования, или подписи, или аутентификации, или идентификации.

Под выражением «достигать, по меньшей мере, данного числа точек» следует понимать то, что рассматриваемую функцию адаптируют для получения на выходе, по меньшей мере, этого данного числа разных точек.

Благодаря этим отличительным признакам, в электронном компоненте можно выполнять криптографическое вычисление, которое основано на точках эллиптической кривой, не давая при этом информации возможному хакеру и поддерживая при этом повышенный уровень эффективности выполнения. Действительно, поскольку функция, позволяющая получить точку на эллиптической кривой, является рациональной дробью, за счет этого она является детерминистической функцией, а не вероятностной; время, необходимое для ее вычисления, является постоянным при любом входном параметре. В этих условиях получение точек на эллиптической кривой является эффективным, и время вычисления больше не зависит от кодируемого сообщения в отличие от известных решений.

Кольцо А может быть кольцом RSA (от "Rivest Shamir Adieman" на английском языке). В этом случае это кольцо можно записать как Z/qZ, где q равно произведению двух простых чисел, при котором вычисление φ(А) затруднено.

Необходимо отметить, что функция Эйлера φ на кольце А является функцией, дающей число обратимых элементов в этом кольце А. В случае, когда А является конечным полем F_q, получаем:

φ(A)=q-1

Подставляя в цикл Z/qZ целых чисел по модулю q, где q является положительным целым числом, являющимся произведением числа I разных простых чисел, строго превышающих 3, при этом I является целым числом, превышающим или равным 2, получаем:

φ(А)=ppcm(p₁ - 1, р₂ - 1,…, p_i - 1)

где ppcm обозначает наименьшее общее кратное, и

р_i являются I простыми числами.

Учитывая, что согласно варианту выполнения настоящего изобретения детерминистическую функцию выражают в виде рациональных дробей, их применение всегда занимает одинаковое время, независимо от сообщения или данных, для которых ее применяют.

Действительно, во множестве А функции возведения в степень 3 и 1/3 являются биективными. Следовательно, их можно записать в виде рациональных дробей и, таким образом, детерминистическую функцию f можно записать в виде рациональных дробей. Во множестве А вычисление показателя степени 1/3 является таким же, как и при вычислении показателя степени (2φ(а)+1)/3. Последний является целым числом, так как φ(А)mod3=1. На множестве А справедливо следующее уравнение:

х^φ(A)=1

Из этого уравнения выводят следующее уравнение:

(x³)^{(2φ(А)+1)/3}=x^{3(2φ(А)+1)/3}=x^2φ(A)+1=x

Следовательно, можно записать:

x^(2φ(A)+1)/3=x^1/3

Однако функция f, которая позволяет получить точку Р эллиптической кривой, содержит это возведение в степень 1/3.

Таким образом, благодаря тому, что функцию возведения в степень 1/3 вычисляют за постоянное время при любом элементе совокупности А, можно получать точки эллиптической кривой, не прибегая к рассмотрению вероятностей. Следовательно, время выполнения криптографического вычисления не зависит от сообщения, на котором производят вычисление, как это происходит в случае вероятностного применения такого вычисления в известных решениях.

Кроме того, в случае, когда А соответствует конечному полю F_q, детерминистическая функция f может давать, по меньшей мере, q/4 точек Р эллиптической кривой. В случае, когда А соответствует кольцу Z/qZ целых чисел по модулю q, где q является положительным целым числом, являющимся произведением числа I разных простых чисел, строго превышающих 3, при этом I является целым числом, превышающим или равным 2, детерминистическая функция f может давать по меньшей мере q/4^I точек Р эллиптической кривой.

Такое число точек на эллиптической кривой, полученных детерминистическим путем, обеспечивает многочисленные варианты криптографического применения с повышенным уровнем защиты от возможных атак.

В варианте выполнения настоящего изобретения используемая эллиптическая кривая является кривой типа Вейерштрасса или так называемой кривой характеристики р. В данном случае считают, что q отличается от 2ⁿ.

Формулу (1) можно записать:

Y²=X³+аХ+b, при а=а₂ и b=а₆.

Детерминистическая функция дает координаты точки эллиптической кривой согласно следующим соответствующим формулам:

X = ( ν 2 − b − u 6 27 ) ( 2 ϕ ( A ) + 1 ) / 3 + u 2 3              (4)

и

Y = u x + ν                                (5)

где u является параметром, определенным на этапе /а/, и

где ν=(3а-u⁴)/(6u)

В другом варианте выполнения настоящее изобретение применяют к эллиптическим кривым характеристик 2.

В этом случае q удовлетворяет формуле:

q=2ⁿ;

где n является нечетным целым числом,

и формулу (1) записывают в виде:

Y²+XY=X³+аХ²+b, при а=а₂ b=а₆; и

детерминистическая функция дает координаты точки эллиптической кривой согласно следующим соответствующим формулам:

X = ( w 4 + w 3 + b ) ( 2 ϕ ( A ) + 1 ) / 3 + w                   (16)

Y=uX+w²

где u является параметром, определенным на этапе /а/, и

где w=a+u²+u.

В предпочтительном частном варианте n является нечетным целым простым числом. Действительно, такое n позволяет ограничить определенные атаки.

В этом контексте предпочтительно детерминистическая функция может давать по меньшей мере 2^n-2 точек Р эллиптической кривой.

Предпочтительно эту функцию можно применить к эллиптическим кривым типа Коблитца, то есть для частного случая эллиптических кривых характеристик 2, в котором b равно 1, и а принадлежит к F₂. Действительно, используя эллиптические кривые Коблитца, можно более быстро производить криптографические вычисления.

Можно предусмотреть применение этой детерминистической функции к результату функции хеширования. Так, на этапе /а/ параметр и можно получить посредством применения функции хеширования h.

В варианте выполнения функция хеширования является функцией с одним направлением. Это свойство сохраняется: функция, получаемая из комбинации детерминистической функции и функции хеширования, имеет это свойство однонаправленности.

В данном случае в конечном счете получают функцию на эллиптической кривой, которая имеет единственное направление, такую как функция хеширования. Кроме того, эта функция является устойчивой по отношению к столкновениям.

Можно также применять эту детерминистическую функцию таким образом, чтобы ее нельзя было дифференцировать (или чтобы она имела характеристику "indifferentiable" на английском языке) от произвольной функции, которую можно было бы применить на эллиптической кривой. Эта характеристика имеет преимущество, в частности, когда эту функцию применяют в криптографической схеме, надежность которой подтверждена в модели, где предполагается, что функции хеширования являются произвольными. Действительно, поскольку детерминистическая функция имеет характеристику невозможности дифференцирования от произвольной функции, получают надежную криптографическую схему за счет применения этой функции в этом одном типе криптографической схемы.

На этапе /а/ параметр u можно получить посредством применения первой функции хеширования h и второй функции хеширования h′. Генератор группы точек эллиптической кривой обозначают G. Криптографическое вычисление может содержать применение следующей функции:

f(h)+h′.G,

где f является детерминистической функцией, и

где G является генератором группы точек эллиптической кривой.

Эта группа точек эллиптической кривой может соответствовать точкам, которые используют в криптографическом вычислении согласно варианту выполнения настоящего изобретения.

Вторым объектом настоящего изобретения является способ аутентификации при помощи, по меньшей мере, одного пароля, применяющий способ выполнения криптографического вычисления по первому объекту настоящего изобретения, в котором на этапе /а/ определяют параметр в зависимости от пароля, при этом указанный пароль включен в параметр, и в котором этап аутентификации осуществляют на основании точки P.

Третьим объектом настоящего изобретения является способ шифрования данных, при этом указанное шифрование основано на тождестве Бонеха-Франклина на эллиптической кривой, допускающем операцию сопряжения; где тождество является цифровым значением, идентифицирующим информационный объект,

при этом указанный способ содержит следующие этапы:

/а/ получают точку посредством применения к тождеству способа выполнения криптографического вычисления по п.6;

/b/ получают шифрованные данные, комбинируя указанную точку, произвольный параметр и указанные данные.

В данном случае под термином «комбинировать» следует понимать применение комбинации операций сопряжения, хеширования, операции «исключающее ИЛИ» и скалярного умножения.

Четвертым объектом настоящего изобретения является способ выполнения криптографического вычисления в электронном компоненте, содержащий этап получения точек Р на эллиптической кривой, при этом справедлива следующая формула:

Y 2 + a 1 X Y + a 3 Y = X 3 + a 2 X 2 + a 4 + X + a 6               (1)

где a₁, а₂, а₃, а₄ и а₆ являются элементами множества А элементов,

где А является кольцом Z/qZ целых чисел по модулю q, где q является положительным целым числом, являющимся произведением числа I разных простых чисел, строго превышающих 3, при этом I является целым числом, превышающим или равным 2, или А является конечным полем F_q с показателем степени q простого целого числа;

где Х и Y являются координатами точек Р и являются элементами А,

при этом указанный способ содержит следующие этапы:

/а/ определяют точку Р с координатами Х и Y на эллиптической кривой;

/b/ получают параметр посредством применения некоторой функции к точке Р; при этом функция φ Эйлера для множества А удовлетворяет следующему равенству:

φ(А)mod3=1,

причем указанная функция является обратной функцией детерминистической функции, выраженной рациональной дробью в а₁, а₂, а₃, а₄ и a₆ и в указанном параметре в А и достигающей по меньшей мере числа d/4^I точек Р при I, равном 1 для конечного поля F_q;

/с/ указанную точку Р используют для применения в криптографии для шифрования, или хеширования, или подписи, или аутентификации, или идентификации.

В данном случае необходимо отметить, что детерминистическая функция по первому объекту настоящего изобретения является обратимой функцией. В связи с этим ее можно предпочтительно использовать в направлении, обратном использованию в этом первом объекте настоящего изобретения. Действительно, ее можно применять в области криптографии на основе точек эллиптической кривой для получения параметра, который им соответствует, через функцию, обратную функции, указанной в первом объекте, в частности, для применения уплотнения данных.

Таким образом, пятым объектом настоящего изобретения является способ уплотнения данных, в котором предназначенные для уплотнения данные соответствуют парам данных Х и Y, соответствующим координатам точек Р эллиптической кривой, удовлетворяющей следующему равенству:

Y 2 + a 1 X Y + a 3 Y = X 3 + a 2 X 2 + a 4 + X + a 6               (1)

где а₁, а₂, a₃, a₄ и a₆ являются элементами множества А элементов,

где А является кольцом Z/qZ целых чисел по модулю q, где q является положительным целым числом, являющимся произведением числа I разных простых чисел, строго превышающих 3, при этом I является целым числом, превышающим или равным 2, или А является конечным полем F_q с показателем степени q простого целого числа;

где Х и Y являются координатами точек Р и являются элементами множества А,

при этом для каждой из указанных пар данных применяют этапы /а/-/с/ способа выполнения криптографического вычисления согласно четвертому объекту настоящего изобретения,

причем указанные пары данных представлены параметрами, соответственно полученными на этапе /с/.

Шестым объектом настоящего изобретения является электронное устройство, содержащее средства, предназначенные для применения способа выполнения криптографического вычисления согласно первому объекту настоящего изобретения.

Седьмым объектом настоящего изобретения является электронное устройство, содержащее средства, предназначенные для применения способа выполнения криптографического вычисления согласно четвертому объекту настоящего изобретения.

Восьмым объектом настоящего изобретения является электронная карта, содержащая электронное устройство согласно шестому и седьмому объектам настоящего изобретения.

Другие отличительные признаки, цели и преимущества изобретения будут более очевидны из нижеследующего описания одного из вариантов его выполнения.

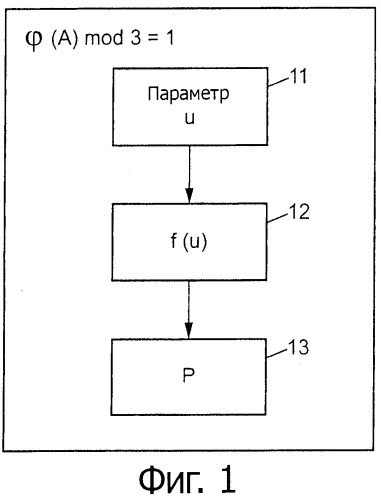
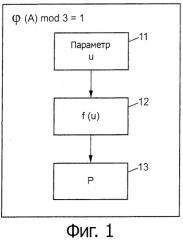
Описание изобретения представлено со ссылками на фиг.1, которая иллюстрирует основные этапы криптографического вычисления согласно варианту выполнения настоящего изобретения.

Любая эллиптическая кривая на множестве А удовлетворяет следующему равенству:

Y 2 + a 1 X Y + a 3 Y = X 3 + a 2 X 2 + a 4 + X + a 6               (1)

где a₁, а₂, a₃, а₄ и а₆ являются элементами множества А,

и где Х и Y являются элементами множества А.

Если справедливо следующее равенство:

φ(А)=1mod3, (2)

где φ является функцией Эйлера, применяемой к множеству А, то функция возведения в степень 3 и функция возведения в степени 1/3 являются функциями, эффективно вычисляемыми за постоянное время при любых значениях, для которых их вычисляют. Это свойство позволяет получить детерминистическим путем точку Р эллиптической кривой в зависимости от некоторого параметра, при этом время вычисления не зависит от указанного параметра, к которому применяют эту детерминистическую функцию f.

В дальнейшем эта функция f будет обозначаться также f_a,b или f_a в зависимости от типа уравнения рассматриваемых эллиптических кривых.

На фиг.1 на этапе 11 показано определение параметра u, являющегося элементом рассматриваемого конечного поля F_q. Затем к этому параметру на этапе 12 применяют детерминистическую функцию f, чтобы в конечном счете детерминистическим образом получить точку Р эллиптической кривой. Все эти этапы осуществляют на кольце А, удовлетворяющем равенству (2).

В следующих разделах представлено применение этих свойств к частным случаям уравнений эллиптической кривой. Вариант выполнения настоящего изобретения можно применить к эллиптическим кривым типа Вейерштрасса, то есть по характеристике р при р>3, и к эллиптическим кривым по характеристикам 2.

В следующих разделах рассматриваемой эллиптической кривой является кривая Вейерштрасса над полем F_q.

В этом контексте мощность q конечного поля Галуа равна рⁿ при простом числе р, отличном от значений 2 и 3. Уравнение (1) можно записать в виде следующего уравнения Вейерштрасса:

Y 2 = X 3 + a X + b                            (3)

где а и b являются параметрами эллиптической кривой, обозначенной Е_а,b.

В конечном поле А=F_q, содержащем число q элементов, где q удовлетворяет равенству (2), функция f возведения в степень 3 и функция возведения в степень 1/3 являются биекциями, эффективно вычисляемыми за постоянное время при любых значениях, по которым их вычисляют.

В этих условиях координаты Х и Y точки Р эллиптической кривой удовлетворяют следующим соответствующим равенствам:

X = ( ν 2 − b − u 6 27 ) ( 2 ϕ ( A ) + 1 ) / 3 + u 2 3              (4)

и

Y = u x + ν                                (5)

Y = u X + ν                               (6)

где u является параметром согласно варианту выполнения настоящего изобретения, причем и принадлежит к конечному полю F q * .

Следует отметить, что в конечном поле F_q возведение в степень ((2φ(А)+1)/3 соответствует возведению в степень 1/3.

Таким образом, в случае, когда эллиптическая кривая, используемая для криптографического вычисления, является кривой Вейерштрасса, предпочтительно точки Р эллиптической кривой можно получить в зависимости от параметра и по уравнениям (4) и (5) детерминистическим образом при постоянном времени вычисления относительно параметра u.

Действительно, точка Р с координатами, удовлетворяющими равенствам (4) и (5), соответствует единственной точке эллиптической кривой по уравнению (3), так как пересечение прямой по равенству (5) с рассматриваемой эллиптической кривой (3) соответствует следующей системе уравнений:

Y 2 = X 3 + a X + b                          (7)

и Y = u X + ν                              (5)

Эту систему уравнений можно записать следующим образом:

X 3 − u 2 X 2 + ( a − 2 u ν ) X + b − ν 2 = 0           (8)

Y = u X + ν                               (6)

Эти последние уравнения можно еще упростить следующим образом:

X 3 − u 2 X 2 + ( u 4 3 ) X + b − ν 2 = 0               (9)

Y = u X + ν                               (6)

Таким образом, в конечном итоге эту систему уравнений можно записать:

( X − u 2 3 ) 3 + b − ν 2 + u 6 27 = 0                 (10)

Y = u X + ν                               (6)

Поскольку уравнение (10) соответствует уравнению (4), можно сделать вывод, что Р является точкой рассматриваемой эллиптической кривой,

Следовательно, точка Р, координаты Х и Y которой удовлетворяют уравнениям (4) и (5), является точкой эллиптической кривой по уравнению (3).

При этом обозначим:

- f_a,b функцию, которая приводит в соответствие с элементом F q * точку эллиптической кривой (3).

0 не может быть входом f_a,b, в противном случае было бы возможно деление на 0. Тем не менее, поскольку нейтральный элемент группы точек эллиптической кривой нельзя получить посредством f_a,b, определяют, что 0 на f_a,b соответствует нейтральному элементу группы точек.

Функция f_a,b является детерминистической функцией, когда функция возведения в степень 3 или возведения в степень 1/3 является биективной функцией в рассматриваемом конечном поле Галуа. Можно отметить, что применение такой функции f_a,b в этих условиях приблизительно соответствует возведению в степень в конечном поле F_q.

Чтобы декодировать сообщение, которое было закодировано при помощи вычисления, произведенного в варианте выполнения настоящего изобретения, предусматривают определение одного или нескольких значений параметра u, который позволил получить данную точку Р эллиптической кривой.

Для этого в следующих разделах указано, как вычислять функцию, обратную функции f_a,b.

Предположим, что u₁ и u₂ являются двумя элементами F q * , причем каждый из них является решением следующего уравнения:

u 4 − 6 u 2 x + 6 u y − 3 a = 0                        (11)

где а, x и y являются элементами F_q.

b удовлетворяет следующему равенству:

b=y²-x³-ах

При этих условиях справедливо следующее равенство:

f a , b ( u 1 ) = ( x 1 , y 1 ) = f a , b ( u 2 ) = ( x 2 , y 2 ) = f a , b ( u ) = ( x , y )          (12)

Действительно, прежде всего все точки P₁ с координатами (x₁, y₁), Р₂ с координатами (х₂, y₂) и Р с координатами (x, y) являются точками эллиптической кривой Е_a,b.

Кроме того, согласно уравнению (11) точки Р и P₁ находятся на прямой, определяемой следующим уравнением:

Y = u 1 X + 3 a − u 1 4 6 u 1                                     (13)

Однако, как было указано выше, поскольку q удовлетворяет равенству (2), эллиптическая кривая (3) и прямая (13) пересекаются только в одной точке. Таким образом, точки Р и P₁ соответствуют одной единственной точке.

Применив эти же рассуждения к точкам Р и Р₂, можно сделать вывод, что точки Р и P₂ тоже соответствуют одной точке эллиптической кривой.

Таким образом, существует параметр u, при котором:

f_a,b(u)=(x,y)

если и только если параметр u является решением уравнения (11).

Таким образом, решение уравнения (11) позволяет определить параметр u, в зависимости от которого получают точку Р эллиптической кривой по следующему уравнению:

f_a,b(u)=P

Уравнение (11) можно решать при помощи обычных алгоритмов, таких как алгоритм Берлекампа [Shoup, Journal of Symbolic Computation Vol.20, p.363-397, 1995]. Благодаря этому уравнению (11) можно легко инвертировать функцию f_a,b, чтобы найти параметр u, который соответствует точке Р эллиптической кривой.

Это свойство позволяет также ограничить достигаемое число точек значением f_a,b. Предположим, что Im(f_a,b) является совокупностью точек отображения функции f_a,b. Множество отображения Im(f_a,b) имеет мощность, меньшую чем q, поскольку q является кардиналом F_q. Кроме того, уравнение (11) позволяет показать, что для каждой точки отображения существует максимум 4 антецедента. По сути дела, мощность не превышает 4-кратную мощность Im(f_a,b). В результате получают следующее неравенство:

q/4≤#Im(f_a,b)≤q

Можно также получить эвристический результат в отношении мощности Im(f_a,b). Уравнение (11) является уравнением 4-ой степени в конечном поле. В конечном поле F_q существует вероятность 2/5 того, что некоторый полином 4-й степени не имеет корня. Следовательно, можно считать, что 3/5 точек эллиптической кривой входят во множество точек отображения Im(f_a,b) и поэтому их можно использовать в криптографическом вычислении согласно варианту выполнения настоящего изобретения.

В варианте выполнения настоящего изобретения можно использовать эллиптические кривые на кольце Z/qZ, где q является произведением I простых чисел p₁, …, p_I. Китайская теорема об остатках, результат модулярной арифметики, рассматривающая решение системы конгруэнтностей, утверждает, что Z/qZ является изоморфным к Z/p₁Z x… x Z/p_IZ. Поэтому можно в равной степени исследовать эллиптические кривые на каждом из Z/p_iZ. Однако, поскольку каждое р_i является простым числом, то по сути дела Z/p_iZ является полем, которое можно обозначить F_pi. Кроме того, поскольку каждое р_i строго превышает 3, уравнение эллиптической кривой на F_pi является уравнением типа Вейерштрасса.

Таким образом, поскольку формулы (4) и (5) верны для каждого из F_pi, то они будут также верны и для F_1i x … x F_pI=Z/qZ.

Кроме того, для каждого из F_pi

p_i/4≤#Im(f_a,b)≤p_i

Это позволяет доказать, что на Z/qZ

p₁/4 x … x p_I/4=q/4^I≤#Im(f_a,b)≤p₁ x … x p_I=q

В варианте выполнения настоящего изобретения можно также использовать эллиптические кривые по характеристикам 2, которые удовлетворяют следующему уравнению:

Y 2 + X Y = X 3 + a X 2 + b                            (15)

где а и b являются элементами конечного поля Галуа A = F 2 n .

Число n может быть нечетным простым числом, чтобы ограничить возможные атаки.

В данном случае имеем:

2ⁿmod3=2

В данном случае функция возведения в степень 3 и функция возведения в степень 1/3 тоже является биекцией, вычисляемой за постоянное время при любых значениях, к которым ее применяют, на этом конечном поле Галуа.

Обозначим u и w параметры F 2 n , которые удовлетворяют следующему уравнению:

w=а+u²+u

Точки Р с координатами Х и Y, удовлетворяющие соответственно нижеследующим формулам, находятся на эллиптической кривой (15):

X = ( w 4 + w 3 + b ) ( 2 ϕ ( A ) + 1 ) / 3 + w                            (16)

Таким образом, в случае, когда эллиптическая кривая, используемая для применения криптографического вычисления, является кривой характеристики 2, то предпочтительно можно получить точки Р эллиптической кривой в зависимости от параметра u по формулам (16) и (16′), причем детерминистическим образом.

Действительно, точка Р с координатами, удовлетворяющими формулам (16) и (16′), соответствует единственной точке эллиптической кривой по уравнению (15), так как пересечение прямой по формуле (16′) с рассматриваемой эллиптической кривой (15) удовлетворяет следующей системе уравнений:

Y 2 + X Y = X 3 + a X 2 + b                            (15)

Эту систему уравнений можно также записать следующим образом:

X 3 + ( a + u + u 2 ) X 2 + w 2 X + b + w 4 = 0                   (17)

Эти последние уравнения можно еще упростить следующим образом:

X 3 + w X 2 + w 2 X + b + w 4 = 0                           (18)

Таким образом, в конечном счете эту систему уравнений можно записать:

( X + w ) 3 + b + w 3 + w 4 = 0                             (19)

Поскольку уравнение (19) соответствует уравнению (16), то можно сделать вывод, что Р является точкой рассматриваемой эллиптической кривой.

Следовательно, точка Р, координаты Х и Y которой отвечают уравнениям (16) и (16′), является точкой эллиптической кривой по уравнению (15).

Как и в случае эллиптически кривых типа Вейерштрасса, в данном случае тоже можно ограничить число точек, включенных в отображение Im(f_a,b) функции f_a. Это множество Im(f_a,b) содержит не более 2ⁿ элементов, так как это является числом элементов исходной совокупности F 2 n .

Уравнение (16′) можно записать:

0 = Y + a + u X + u 2 + u 4                               (17)

При значении u, которое решает вышеуказанное уравнение, получаем:

f_a(u)=(x,y)

Уравнение (17) является уравнением 4-й степени. Следовательно, это уравнение имеет решение, по меньшей мере, при четырех разных значениях параметра u. Таким образом, мы имеем, по меньшей мере, 2ⁿ/4=2^n-2 точек отображения f_a. Следовательно, во множестве точек отображения Im(f_a) имеется, по меньшей мере, 2^n-2 элементов.

Благодаря отличительным признакам настоящего изобретения получают детерминистическую функцию f, обозначаемую f_a,b или f_a в зависимости от рассматриваемого типа эллиптических кривых, множество от