Способ измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла

Способ измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла

Иллюстрации

Показать все

Реферат

Изобретение относится к области тепловых испытаний твердых материалов, а именно к области исследования теплофизических характеристик этих материалов.

Известен способ определения комплекса теплофизических свойств твердых материалов [Патент РФ №2374631, кл. G01N 25/18, 2008], включающий тепловое импульсное воздействие на плоскую поверхность исследуемого образца и измерение избыточной температуры на плоской поверхности образца в одной точке в заданном интервале времени. Тепловое импульсное воздействие осуществляют лучистым тепловым потоком известной плотности и длительности, а измерение избыточной температуры с момента подачи теплового импульса проводят в центральной части нагреваемой поверхности образца, при этом регистрируют значение максимальной избыточной температуры и время ее достижения.

К недостаткам этого способа относятся невысокая точность измерения коэффициента температуропроводности и необходимость наличия специальной аппаратуры (инфракрасного излучателя и инфракрасного измерителя температуры).

Известен способ определения комплекса теплофизических свойств твердых материалов [Патент РФ №2125258, кл. G01N 25/18, 1999], включающий воздействие тепловыми импульсами от линейного источника на плоскую поверхность исследуемого и эталонного образцов, измерение избыточных температур в моменты подачи тепловых импульсов в точках, расположенных на фиксированных расстояниях от линии нагрева на поверхности образцов. Измерение температуры приближают с минимальной погрешностью к рассчитанным температурам, формируемых посредством программного управления параметрами теплофизических характеристик. По идентифицированным параметрам образцов и действительным значениям характеристик эталона определяют искомые характеристики.

Недостатками этого способа являются большая длительность и трудоемкость эксперимента, а также необходимость использования эталонного образца.

Наиболее близким техническим решением является способ измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла [Пономарев, С.В. Теоретические и практические основы теплофизических измерений: монография / под ред. С.В.Пономарева. - М.: ФИЗМАТЛИТ, 2008. - 408 с.], заключающийся в том, что из исследуемого материала изготавливают три пластины, причем одну тонкую толщиной х₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает х₀. Между нижней массивной и тонкой пластинами размещают плоский электронагреватель, изготовленный из тонкой нихромовой (манганиновой) проволоки, а датчик температуры, изготовленный из медной проволоки, располагают на расстоянии x=х₀ от нагревателя. Полученную систему предварительно выдерживают при заданной начальной температуре Т₀ не менее двух часов. Активная часть эксперимента начинается в тот момент времени, когда на электронагреватель подается короткий электрический импульс. За время действия этого импульса в единице площади плоского нагревателя выделяется количество тепла Q_n. В течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке x=х₀, определяют максимальное значение температуры T_max. Активную стадию эксперимента завершают при τ>τ_max, где x_max - момент времени, соответствующий достижению максимального значения температуры T_max. По полученным данным (х₀, Q_n, T_max, τ_max) вычисляют искомые теплофизические свойства исследуемого материала.

Недостатком данного способа является невысокая точность измерения теплофизических свойств исследуемого материала, так как сложно достаточно точно определить значение момента времени τ_max.

Техническая задача изобретения - повышение точности измерения теплофизических свойств твердых материалов за счет выбора оптимальных режимных параметров теплофизического эксперимента.

Техническая задача достигается тем, что в способе измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла, заключающемся в том, что образец исследуемого материала изготавливают в виде трех пластин, причем тонкую пластину толщиной х₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает x₀, в плоскости x=0 между нижней массивной и тонкой пластинами размещают плоский электронагреватель, изготовленный из пермаллоевой фольги, а термоэлектрический преобразователь располагают в другой плоскости на расстоянии x=х₀ от нагревателя между верхней массивной и тонкой пластинами, полученную систему предварительно выдерживают при заданной начальной температуре Т₀, затем на электронагреватель подают короткий электрический импульс, в течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке х=х₀ с постоянным шагом во времени, определяют максимальное значение температуры T_max, в отличие от прототипа, активную стадию эксперимента заканчивают, когда разность температур (T_i-Т₀) становится меньше величины α(T_max-T₀), рассчитывают значение температуры T′=β(T_max-T₀)+T₀, соответствующее заданному значению параметра β, определяют четыре ближайших к T′ значения T_j-1<T_j, T_j≤T′, T_j+1>T′, T_j+2>T_j+1, вычисляют параметры b₀, b₁ зависимости Т=b₀+b₁τ методом наименьших квадратов по четырем парам значений (τ_j-1, T_j-1), (τ_j, T_j-1), (τ_j+1, T_j+1), (τ_j+2, T_j+2), определяют момент времени τ′ как корень уравнения Т′=b₀+b₁τ, а искомые теплофизические свойства рассчитывают по формулам:

;

c ρ = Q n z ' exp ( − z ' ) ( T ' − T 0 ) ⋅ x 0 π ;

λ=acρ,

где a - температуропроводность исследуемого материала; cρ - объемная теплоемкость исследуемого материала; X - теплопроводность исследуемого материала; Q_n - количество тепла, мгновенно выделившееся в единице площади плоского нагревателя в момент начала активной стадии эксперимента; z′ - больший корень уравнения z exp ( − z ) = β 2 e ; значение параметра α выбирают из диапазона 0,95…0,98; значение параметра β выбирают из диапазона 0,3…0,6, причем оптимальным является значение β_опт=0,498.

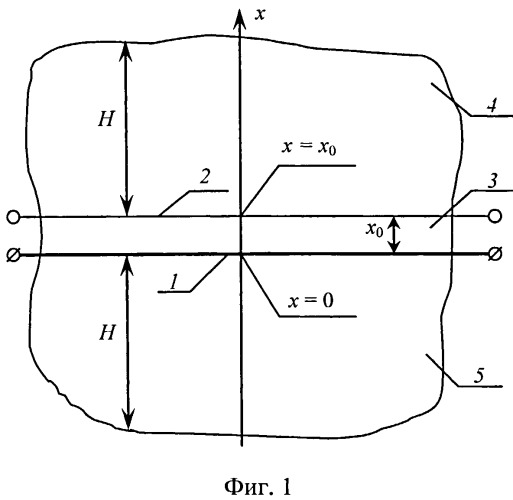
На фиг.1 представлена физическая модель устройства для реализации метода плоского мгновенного источника тепла.

Из исследуемого твердого материала изготавливают три пластины: одну тонкую пластину толщиной х₀, обозначенную на фиг.1 цифрой 3 и две массивные (толстые) пластины, обозначенные цифрами 4 и 5, причем толщина Н этих пластин должна не менее чем в десять-двадцать раз превышать толщину х₀ тонкой пластины 3. Плоский нагреватель 1, изготовленный из тонкой пермаллоевой фольги, размещают между пластинами 3 и 5, а хромель-копелевую термопару 2, обеспечивающую измерение температуры Т(х₀, τ), - с другой стороны, между пластинами 3 и 4. Для уменьшения влияния контактных тепловых сопротивлений нужно обеспечить необходимую силу прижатия пластин к нагревателю 1 и к датчику температуры 2.

Получившуюся систему, включающую в себя пластины 3, 4, 5 с зажатыми между ними нагревателем 1 и измерителем температуры 2, в течение достаточно большого промежутка времени выдерживают при заданной температуре T₀. В абсолютном большинстве случаев для этого требуется не менее двух часов.

Активная часть эксперимента начинается в тот момент времени, когда на электронагреватель 1 подается короткий электрический импульс. За время действия этого импульса в единице площади плоского нагревателя выделяется определенное количество тепла

Q n = ∫ 0 τ и P ( τ ) d τ ≈ P τ и ,

где P - электрическая мощность [Вт/м²], приходящаяся на единицу площади плоского нагревателя; τ_и - длительность импульса.

После действия "мгновенного" источника тепла на протяжении активной стадии эксперимента осуществляют измерение и регистрацию температуры Т(х₀, τ), определяют максимальное значение температуры T_max. Активную стадию эксперимента заканчивают, когда T_i-Т₀≤α(T_max-Т₀), значение параметра α выбирают из диапазона 0,95…0,98.

После завершения активной части эксперимента по полученным данным вычисляют искомые теплофизические свойства исследуемого вещества по расчетным формулам, вывод которых рассмотрим ниже.

Исходя из математической модели данного метода, изложенной в прототипе, можно получить решение, которое имеет следующий вид:

где T(x, τ)- температура в точке с координатой x в момент времени τ; а, с, ρ - соответственно температуропроводность, удельная теплоемкость и плотность исследуемого вещества.

В том же источнике показано, что определение температуропроводности обычно осуществляется по формуле

где τ_max - момент времени, в который достигается максимальное значение температуры T_max.

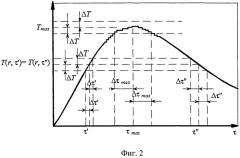
Использование формулы (2) приводит к большим погрешностям, поскольку сложно достаточно точно определить значение момента времени τ_max. Попробуем определить такие моменты времени τ′ и τ′′, используя которые (см. фиг.2), можно минимизировать погрешность определения температуропроводности.

Для этого измерим в точке с координатой x изменение во времени т температуры Т(х, τ) и зарегистрируем эту кривую (фиг.2).

Введем безразмерную переменную . Тогда решение (1) примет вид

,

где объемная теплоемкость исследуемого материала.

Введем переменный параметр

β = T ( x , τ ) − T 0 T max − T 0 .                     ( 3 )

Запишем решение (1) для момента времени τ′=τ′(β):

T ( x , τ ' ) − T 0 = Q n z ( τ ' ( β ) ) exp ( − z ( τ ' ( β ) ) ) c ρ ⋅ x π .                               ( 1 a )

Для момента времени τ=τ_max, когда z | τ max = 1 2 , получаем

T ( x , τ max ) − T 0 ≡ T max − T 0 = Q n 1 2 exp ( − 1 2 ) c ρ ⋅ x π = Q n c ρ ⋅ x 2 π e .                               ( 1 b )

Поделив (1а) на (1b), получаем

β = T ( x , τ ' ( β ) ) − T 0 T max − T 0 = z 1 2 exp [ − z ] 2 e .                     ( 4 )

Преобразовав выражение (4), получаем уравнение

z ⋅ exp [ − z ] = β 2 e .                     ( 5 )

Обозначим z′=z(x′(β)) и z′′=z(τ′′(β)) соответственно больший и меньший корни уравнения (5). После преобразований легко получаем формулы для вычисления искомой температуропроводности а по экспериментально измеренным значениям моментов времени τ′ и τ′′:

из следует, что

из следует, что

где τ′ и τ′′ - меньший и больший моменты времени, соответствующие большему Jz′ и меньшему z′′ корням уравнения (5), при которых достигается заданное значение параметра β, определенное формулой (3).

Для вычисления объемной теплоемкости сρ на основе зависимости (1а) легко получается формула:

с ρ = Q n z ( τ ' ( β ) ) exp ( − z ( τ ' ( β ) ) ) [ T ( x , τ ' ( β ) ) − T 0 ] x π ,                           ( 7 )

которая при z | τ max = 1 2 , с учетом (1b) принимает вид:

с ρ = Q n [ T max − T 0 ] x π .                     ( 7 a )

Теплопроводность исследуемого материала λ определяется по формуле

Значение параметра β выбирают из диапазона 0,3…0,6, причем оптимальным является значение β_oпт=0,498.

С учетом вышеизложенного, обработка экспериментальных данных после завершения активной стадии эксперимента производится в следующей последовательности:

- рассчитывается значение температуры T′=β(T_max-Т₀)+Т₀, параметр β выбирается из диапазона 0,3…0,6;

- определяются четыре ближайших к T′ значения T_j-1<T_j, T_j≤T′, T_j+1>T′, T_j+2>T_j+1;

- вычисляются параметры b₀, b₁ зависимости Т=b₀+b₁τ методом наименьших квадратов по четырем парам значений (τ_j-1, T_j-1), (τ_j, T_j), (τ_j+1, T_j+1), (τ_j+2, T_j+2);

- определяется момент времени τ′ как корень уравнения Т′=b₀+b₁τ;

- вычисляется значение z′ как больший корень уравнения (5);

- искомые теплофизические свойства рассчитываются по формулам (6), (7) и (8).

Способ измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла, заключающийся в том, что образец исследуемого материала изготавливают в виде трех пластин, причем тонкую пластину толщиной x₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает x₀, в плоскости х=0 между нижней массивной и тонкой пластинами размещают плоский электронагреватель, изготовленный из пермаллоевой фольги, а термоэлектрический преобразователь располагают в другой плоскости на расстоянии x=x₀ от нагревателя между верхней массивной и тонкой пластинами, полученную систему предварительно выдерживают при заданной начальной температуре Т₀, затем на электронагреватель подают короткий электрический импульс, в течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке х=х₀ с постоянным шагом во времени, определяют максимальное значение температуры T_max, отличающийся тем, что после достижения максимального значения температуры T_max активную стадию эксперимента заканчивают, когда разность температур (T_i-T₀) становится меньше величины α(T_max-T₀), рассчитывают значение температуры T′=β(T_max-T₀)+T₀, соответствующее заданному значению параметра β, определяют четыре ближайших к T′ значения T_j-1<T_j, T_j≤T′, T_j+1>T′, T_j+2>T_j+1, вычисляют параметры b₀, b₁ зависимости Т=b₀+b₁τ методом наименьших квадратов по четырем парам значений (τ_j-1, T_j-1), (τ_j, T_j-1), (τ_j+1, T_j+1), (τ_j+2, T_j+2), определяют момент времени τ′ как корень уравнения Т′=b₀+b₁τ, а искомые теплофизические свойства рассчитывают по формулам: ; c ρ = Q n z ' exp ( − z ' ) ( T ' − T 0 ) ⋅ x 0 π ;λ=acρ; а - температуропроводность исследуемого материала;сρ - объемная теплоемкость исследуемого материала;λ - теплопроводность исследуемого материала;Q_n - количество тепла, мгновенно выделившееся в единице площади плоского нагревателя в момент начала активной стадии эксперимента;z′ - больший корень уравнения z exp ( − z ) = β 2 e ;значение параметра α выбирают из диапазона 0,95…0,98;значение параметра β выбирают из диапазона 0,3…0,6, причем оптимальным является значение β_опт=0,498.