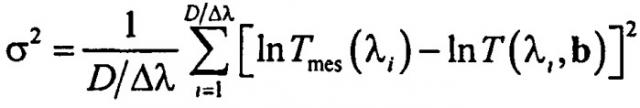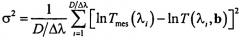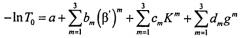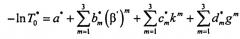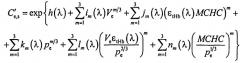Способ определения содержания производных гемоглобина в крови

Способ определения содержания производных гемоглобина в крови

Иллюстрации

Показать все

Реферат

Изобретение относится к медицинской диагностике в области гематологии и может быть использовано для контроля газового состава крови в реанимации, токсикологии, при интенсивной терапии, для определения влияния на гемоглобинный состав физиологических, патологических и экологических факторов, а также в родильных домах, акушерских и педиатрических стационарах для контроля гематологических показателей новорожденных и мониторинга гипербилирубинемии.

Известен способ для определения оксигенации гемоглобина в оптически доступных тканях [1]. Для проведения оксиметрии исследуют избранную зону ткани. С помощью коллимированного зондирующего света двух определенных длин волн в полосе поглощения гемоглобина вокруг изобестической длины волны поглощения около 501 нм измеряют интенсивность отраженного зондирующего света от ткани, определяют адекватные насыщению кислородом коэффициенты отражения для изобестической и неизобестической длин волн и по их значениям определяют оксигенацию гемоглобина. Недостатком этого способа является определение лишь степени оксигенации гемоглобина, не позволяющее проводить более полную диагностику состояния пациента. Кроме того, при расчетах пренебрегают содержанием карбоксигемоглобина и метгемоглобина, что в некоторых случаях существенно снижает точность оксиметрии. Способ не может быть использован при исследовании патологических состояний.

Известен способ определения относительных концентраций производных гемоглобина [2], включающий помещение проб крови в две кюветы с различной величиной оптического пути, измерение коэффициентов диффузионного отражения и относительного пропускания двух слоев на длинах волн 660, 700, 805 нм, расчет относительных концентраций мет-, окси-, и дезоксигемоглобина по установленным значениям оптических плотностей слоя крови на фотометрируемых длинах волн. Достоинством этого способа является учет при расчетах диффузионного рассеяния, что повышает точность получаемых результатов; а также определение трех производных гемоглобина, в том числе метгемоглобина, что позволяет использовать данный способ при ряде острых отравлений. Известный способ не предусматривает определение содержания карбоксигемоглобина, а также абсолютных концентраций исследуемых производных гемоглобина, что существенно снижает в большинстве случаев его информативность.

Наиболее близким к заявляемому является способ определения содержания производных гемоглобина в крови, основанный на фотометрировании раствора крови на m длинах волн, выбранных методами линейного программирования в диапазоне 450-650 нм, измерении оптической плотности раствора крови на выбранных длинах волн [3]. Концентрации производных гемоглобина, в частности оксигемоглобина, дезоксигемоглобина, карбоксигемоглобина, метгемоглобина, определяют по известным молярным коэффициентам поглощения из системы уравнений, связывающих определяемые параметры с измеренными оптическими плотностями раствора крови. Данный способ позволяет определять абсолютные значения четырех производных гемоглобина. Однако он требует подготовки проб крови (например, ультразвуком под давлением либо с добавлением химического гемолизирующего раствора), что усложняет анализ крови и увеличивает время анализа. Кроме того, данный способ не учитывает содержание сульфгемоглобина в крови, характерная полоса поглощения которого (максимум поглощения на λ=622 нм) перекрывается с характерной полосой поглощения метгемоглобина (максимум поглощения на λ=630 нм), что при некоторых патологических состояниях может служить причиной ошибочного диагноза.

Предлагаемое изобретение направлено на решение задачи расширения функциональных возможностей за счет одновременного определения всех производных гемоглобина (оксигемоглобина, дезоксигемоглобина, карбоксигемоглобина, метгемоглобина, сульфгемоглобина), а также гематокрита и концентрации билирубина в крови; возможности определения производных гемоглобина в цельной крови; повышение точности измерений определяемых параметров.

Для решения данных задач фотометрирование цельной крови осуществляют в видимом и ближнем ИК-диапазоне длин волн, измеряют спектральные коэффициенты пропускания кюветы с цельной кровью, а количественные значения концентрации основных производных гемоглобина определяют путем минимизации невязки

,

где вектор b - определяемые концентрации производных гемоглобина (окси, деокси, карбокси, мет- и сульфгемоглобин), общего гемоглобина, билирубина, а также гематокрит;

T_meas(λ), T(λ_i, b) - соответственно экспериментальные и расчетные значения коэффициентов пропускания крови;

D - используемый диапазон длин волн,

Δλ - используемое спектральное разрешение,

D/Δλ - количество длин волн фотометрирования крови;

,

,

,

где r, r^* - соответственно коэффициенты отражения света от кюветы с кровью и внутренних стенок кюветы;

Т₀, Т^* - соответственно коэффициенты пропускания кровью коллимированного и диффузного излучения;

а средний косинус индикатрисы рассеяния g, транспортный коэффициент рассеяния β′ и коэффициент поглощения k рассчитываются с учетом полученных путем численного моделирования аппроксимационных зависимостей между сечением поглощения и рассеяния C_e,a, , среднего косинуса индикатрисы рассеяния эритроцитов g_e, которые имеют вид:

,

,

,

где ε_tHb - молярный коэффициент поглощения гемоглобина;

МСНС - концентрация гемоглобина в эритроците;

P_e - параметр формы эритроцита;

V_e - средний объем эритроцита,

а a, b, …u - численные коэффициенты, рассчитанные заранее методом наименьших квадратов при аппроксимации указанными выше уравнениями статистических данных о множестве смоделированных связей между оптическими характеристиками, оптическими и биофизическими параметрами крови в известных диапазонах разброса последних.

Сущность данного изобретения поясняется с помощью фиг.1-5. На фиг.1 представлены молярные коэффициенты поглощения производных гемоглобина, на фиг.2 сопоставлены коэффициенты пропускания кюветы с кровью, рассчитанные аналитически и методом Монте-Карло, на фиг.3 приведена гистограмма погрешностей полученных аналитических выражений относительно метода Монте-Карло, на фиг.4 представлены погрешности аналитических расчетов оптических параметров частиц, моделирующих эритроциты крови, на фиг.5 изображен спектр коэффициента пропускания, смоделированный методом Монте-Карло при заданных значениях модельных параметров (точки) и подобранный в результате решения обратной задачи (кривая).

Для получения аналитических соотношений, связывающих спектральные коэффициенты пропускания кюветы с кровью с определяемыми параметрами (концентрациями основных производных гемоглобина и билирубина), требуется использование модели переноса света в крови, позволяющей численно рассчитывать спектр пропускания кюветы с кровью с учетом многократного рассеяние света эритроцитами и возможных вариаций их формы. Рассмотрим эффективность предлагаемого решения на примере тонкой кюветы с цельной кровью (толщиной 200 мкм) при ее направленном освещении. Выбор такой малой толщины связан с тем, что кровь является сильно поглощающей средой и производить ее фотометрирование спектральной в области λ<600 нм, где сосредоточены основные полосы поглощения таких хромофоров крови как билирубин и окси-, деокси- и карбоксигемоглобин (фиг.1), можно только в тонких кюветах.

Модель переноса света в крови. Основными морфологическими и биохимическими параметрами цельной крови, определяющими ее оптические свойства в видимом и ближнем ИК спектральных диапазонах, являются [4-13]:

1) средний объем эритроцита V_e=60-200 мкм³;

2) концентрация гемоглобина в эритроците МСНС=280-380 г/л;

3) параметр формы эритроцита p_e=2-5 (смысл его будет пояснен ниже);

4) объемная концентрация эритроцитов в крови (гематокрит) H=0.2-0.7;

5) гемоглобинный состав, характеризующийся относительными концентрациями оксигемоглобина c_HbO2≤0.98, карбоксигемоглобина - c_COHb≤0-2, метгемоглобина - c_MetHb≤0.2, сульфгемоглобина - c_SHb≤0.1 и деоксигемоглобина c_Hb=1-c_HbO2-c_COHb-c_MetHb-c_SHb;

6) концентрация билирубина (продукта распада гемоглобина) в плазме C_bil≤230 мг/л.

Знание вышеуказанных параметров позволяет рассчитать и ряд других, важных параметров крови, например концентрацию общего гемоглобина в крови C_tHb=МСНС·Н=80-200 г/л и счетную концентрацию эритроцитов (количество эритроцитов в 1 мм³) N_e=H/V_e=(3.5-6.5)·10⁶ мм^-3.

Поскольку гемоглобин неравномерно перемешан в крови, а локализован в эритроцитах, то спектры поглощения цельной и гемолизированной крови существенно различаются [10, 14]. В связи с этим для расчета коэффициентов поглощения и рассеяния цельной крови будем использовать методы теории дифракции света на частицах, моделирующих эритроциты. Для этого необходимо задать размер, форму эритроцитов и спектральную зависимость их комплексного показателя преломления (КПП), а также окружающей их среды (плазмы).

Действительная часть n_e КПП эритроцитов определяется преимущественно содержанием гемоглобина в их составе (МСНС):

где n H 2 O - показатель преломления воды; α - эмпирический коэффициент [15]. Поскольку содержание солей, сахаров и других органических компонентов в цитоплазме эритроцитов незначительно, то при проведении расчетов полагается, что спектральная зависимость цитоплазмы эритроцитов коррелирует со спектральной зависимостью показателя преломления воды [7].

Мнимая часть χ_e КПП эритроцитов связана с молярным коэффициентом поглощения гемоглобина ε_tHb следующим образом [6-10]:

µ_tHb=64.5 г/ммоль - молярная масса гемоглобина; λ - длина волны света в нм. Коэффициент ε_tHb рассчитывается в соответствии с гемоглобинным составом:

где ε_HbO2, ε_Hb, ε_COHb, ε_MetHb и ε_SHb - молярные коэффициенты полгощения соответственно окси- (HbO₂), деокси- (Hb), карбокси- (COHb), мет- (MetHb) и сульфгемоглобина (SHb) в мм^-1/(ммоль/л) [16]. Спектральные зависимости этих коэффициентов представлены на фиг.1. Как видно, спектры поглощения производных гемоглобина существенно перекрываются, причем спектр поглощения COHb практически подобен спектру поглощения HbO₂. В связи с этим для комплексного определения концентраций производных гемоглобина необходимо выполнять измерения спектрального пропускания крови с достаточно малым шагом по λ (чтобы количество спектральных участков во много раз превышало количество анализируемых производных гемоглобина). Это позволяет существенно повысить устойчивость обратной задачи к погрешностям оптических измерений и сузить диапазон равноприемлемых модельных решений (одинаково хорошо воспроизводящих данные измерений в пределах экспериментальной точности).

Спектральная зависимость показателя преломления плазмы крови n_pl в спектральном диапазоне 400-1000 нм описывается эмпирическим выражением [7]:

Эритроциты будем моделировать хаотически ориентированными сплюснутыми сфероидами. В этом случае параметр формы эритроцитов имеет ясную геометрическую интерпретацию и определяется как p_e=a/b, где a и b - большая и малая полуоси оптически-эквивалентного сфероида, обладающего такими же оптическими характеристиками, как и реальный эритроцит. Такое предположение основано на том факте, что сфероидальные частицы позволяют достаточно хорошо аппроксимировать частицы различных форм [8, 17, 18].

Наиболее эффективным методом расчета оптических характеристик хаотически ориентированных сфероидов (коэффициента поглощения, коэффициента рассеяния, индикатрисы рассеяния) является метод Т-матриц [19]. Данный метод обладает наибольшим быстродействием по сравнению с другими методами теории дифракции света на частицах, основанными на строгом решении уравнений Максвелла. Однако использование данного метода для оптически «мягких» частиц с размерами и параметрами формы, характерными для эритроцитов, осложняется плохой сходимостью соответствующих им рядов в расчетных формулах для элементов Т-матрицы. В связи с этим используется упрощенный подход к расчету оптических характеристик оптически «мягких» сфероидов, предложенный в работе [20]. Суть его заключается в переходе от хаотически ориентированного сфероида к набору шаров с распределением по дифракционному параметру типа степенного, плотность которого

где x и xp_e - минимальный и максимальный значения дифракционного параметра сфероида; x=2πb/λ; b - малая полуось сфероида; x₀=2πr₀/λ; r₀ - радиус сферической частицы. В работе [20] путем сравнения с методом Т-матриц показано, что взвесь хаотически ориентированных монодисперсных сфероидальных частиц по своим оптическим свойствам практически не отличается от полидисперсных сферических частиц с плотностью распределения (5). Таким образом, оптические сечения поглощения C_e,a, рассеяния C_e,s и индикатрису рассеяния P_e сфероидальных частиц, моделирующих эритроциты в плазме, можно рассчитать согласно известным правилам сложения соответствующих оптических величин для полидисперсного ансамбля сферических частиц:

где m_e=(n_e+iχ_e)/n_pl - относительный КПП эритроцитов; C_a, C_s и S₁₁ - оптические сечения поглощения, рассеяния и индикатриса рассеяния сферической частицы; θ - угол рассеяния.

При плотной упаковке частиц, как это имеет место в случае цельной крови, необходимо учитывать влияние интерференционного сложения волн, рассеянных соседними частицами, на объемные коэффициенты поглощения k, рассеяния β и индикатрису рассеяния Р(θ) среды. Учет кооперативного взаимодействия плотноупакованных эритроцитов является далеко не тривиальной задачей, требующей дальнейших экспериментальных и теоретических исследований. Немногочисленные экспериментальные данные по зависимостям оптических параметров крови от объемной концентрации эритроцитов (H), имеющиеся в литературе [21, 22], демонстрируют практически линейную зависимость коэффициента k от H (по крайней мере, в диапазоне H=0-0.45). Исходя из этих данных коэффициент поглощения крови k будем рассчитывать как сумму коэффициентов поглощения суспензии эритроцитов (пропорционального H) и растворенного в плазме билирубина:

где ε_bil - молярный коэффициент поглощения билирубина в мм^-1/(ммоль/л) [23]; µ_bil=585 мг/ммоль - молярная масса билирубина.

Экспериментальные зависимости β от H являются линейными лишь до H<0.1. Для более высоких значений H экспериментальные данные существенно расходятся, что, по-видимому, связано с большими погрешностями определения коэффициента β при большой оптической плотности исследуемого вещества [21]. Очевидно, что в пределе H→1, когда эритроциты слипаются вместе, образуя однородную массу поглощающего гемоглобина, коэффициент рассеяния крови должен стремиться к нулю. Это приводит к следующему приближенному выражению для β [24]:

где множитель (1-H) отвечает за подавление рассеяния при H→1.

Что касается влияния плотности упаковки эритроцитов на индикатрису рассеяния крови Р(θ), то имеющиеся в литературе данные относятся лишь к ее среднему косинусу и также существенно отягощены погрешностями измерений [21]. В связи с этим будем полагать, что эффекты кооперативного взаимодействия эритроцитов не оказывают значимого влияния на индикатрису рассеяния крови, поэтому Р(θ)=Р_е(θ). Отметим, что это предположение используется практически во всех известных работах по моделированию процесса переноса света в цельной крови [4-10].

Расчет характеристик переноса света в кювете с кровью осуществляется с использованием метода Монте-Карло [25, 26], основанного на статистическом моделировании траекторий большого количества фотонов от точки их влета в среду до их поглощения или вылета из среды. Первоначальный ″вес″ каждого фотона равен единице. При ″блуждании″ фотона в среде его ″вес″ уменьшается за счет френелевского отражения от поверхности среды (в данном случае от стенок кюветы), а также за счет процессов поглощения и рассеяния в среде. Коэффициент пропускания кюветы с кровью рассчитывается как отношение суммарного ″веса″ фотонов, попавших на приемник излучения или объектив камеры, к суммарному числу фотонов, падающих на среду.

Метод расчета спектрального пропускания крови.

Вышеописанная модель позволяет по известным значениям морфологических и биохимических параметров крови численно рассчитывать спектр пропускания крови и другие ее оптические характеристики, измеряемые в эксперименте, т.е. решать прямую задачу. Однако для количественной интерпретации получаемых в эксперименте результатов требуется многократное решение прямой задачи при различных значениях модельных параметров, что является весьма трудоемким даже для современной вычислительной техники. В связи с этим нами разработан простой метод расчета спектрального пропускания крови, позволяющий выполнять интерпретацию результатов спектрофотометрических измерений в режиме реального времени. Аналитические выражения, используемые в данном методе, получены на основе аппроксимации данных, рассчитанных с использованием вышеописанной модели при различных значениях модельных параметров (структурных и биохимических параметров крови).

Моделирование выполнялось для слоя цельной крови толщиной 200 мкм. В численных расчетах принимается, что пучок излучения, состоящий из 10⁶ фотонов, падает нормально на стеклянную кювету с показателем преломления n_gl=1.5, а приемник излучения регистрирует все фотоны, прошедшие через кювету. Разумеется, что методом Монте-Карло можно проводить вычисления фотометрических сигналов, соответствующих и любой другой геометрии эксперимента.

Оптические параметры крови (Р(θ), k и β) и коэффициент пропускания (КП) кюветы с кровью T(λ) рассчитывались в диапазоне λ=450-850 нм с шагом 5 нм. Расчет проведен для 750 случайных реализации модельных параметров, соответствующих вышеуказанным диапазонам их вариаций (с учетом ограничений по зависящим от них параметрам C_tHb и N_e). Смоделированные данные использовались для получения аналитических выражений, аппроксимирующих зависимости КП крови от ее оптических параметров, а также оптических параметров от структурных и биохимических параметров.

Общий вид выражения для КП кюветы с кровью выбран исходя из физических соображений. Фотоны на своем пути через слой крови испытывают большое количество актов рассеяния даже при малой толщине слоя, в результате чего излучение существенно отклоняется от своего первоначального направления. У стенок кюветы и будем считать это излучение полностью диффузным. Такое упрощение позволяет достаточно просто учесть многократные переотражения света между стенками кюветы. Действительно, в этом случае коэффициент отражения света от внутренних стенок кюветы (r^*) не зависит от оптических параметров крови, и полный поток излучения, прошедшего через кювету, можно найти как сумму переотраженных потоков, образующих бесконечно убывающую геометрическую прогрессию со знаменателем , где - коэффициент пропускания кровью диффузного излучения. Искомый КП определяется как отношение прошедшего через кювету диффузного потока к падающему на нее направленному потоку:

где r - френелевский коэффициент отражения коллимированного излучения от кюветы с кровью, T₀ - коэффициент пропускания кровью коллимированного излучения. Несоответствие коэффициента r^* в формуле (11) угловой структуре излучения у стенок кюветы можно учесть в зависимостях коэффициентов Т₀ и от оптических параметров крови. Исходя из вышеописанных расчетов КП методом Монте-Карло эти зависимости хорошо аппроксимируются полиномами следующего вида:

где g - средний косинус индикатрисы рассеяния; β′=β(1-g) - транспортный коэффициент рассеяния. Значения коэффициентов в формулах (12), (13) указаны в табл.1.

Значения оптических параметров цельной крови, при которых справедливы полученные выражения, охватывают, по меньшей мере, следующие диапазоны: k=0.1-28 мм^-1, β=79-232 мм^-1, β′=0.7-3.5 мм^-1, g=0.977-0.997, Т=0.001-0.779. Данные диапазоны соответствуют λ=450-850 нм и вышеуказанным вариациям морфологических и биохимических параметров крови. О точности расчетов Т(λ) с использованием выражений (11)-(13) можно судить на основании их сравнения с вышеописанными численными расчетами T(λ) методом Монте-Карло. На фиг.2 сопоставлены значения КП, рассчитанные численно - T_MC и аналитически - T, при различных значениях оптических параметров крови, а на фиг.3 изображено распределение v(δ_T) соответствующих им погрешностей δ T = 100 % ⋅ | T − T M C | / T M C . Как видно, различие между коэффициентами T_МС и T находится в пределах погрешности фотометрических измерений, причем в среднем δ_T≈0.5%. Следует отметить, что выражения (11)-(13) можно с успехом использовать для аппроксимации коэффициента пропускания, соответствующего любой апертуре фотоприемника. Отличия будут заключаться лишь в численных значениях коэффициентов аппроксимации.

Как следует из выражений (11)-(13), коэффициенты пропускания тонкой кюветы с кровью определяется коэффициентом поглощения k, транспортным коэффициентом рассеяния β′ и средним косинусом g индикатрисы рассеяния крови. В вышеописанных численных расчетах данных характеристик наиболее трудоемким является этап расчета сечений поглощения (С_е,a), рассеяния (C_e,s) и индикатрисы рассеяния Р_е(θ) эритроцитов по формулам (6)-(8). Очевидно, для количественного анализа спектра пропускания цельной крови необходим оперативный метод расчета оптических характеристик эритроцитов. В связи с этим нами получены выражения, с высокой точностью аппроксимирующие зависимости g_e, С_е,а и С′_e,s=С_е,s(1-g_e) от морфологических параметров и биохимического состава эритроцитов:

где a, b, …, u - численные коэффициенты, рассчитанные заранее методом наименьших квадратов в диапазоне λ=450-850 нм (видимый и ближний ИК-диапазон) с шагом 5 нм при аппроксимации указанными выше уравнениями статистических данных о множестве смоделированных связей между оптическими характеристиками, оптическими и биофизическими параметрами крови в известных диапазонах разброса последних.

Средние погрешности аппроксимации спектральных зависимостей C_e,a(λ), и g_e(λ) выражениями (14)-(16) приведены на фиг.4. При известных значениях C_e,a и C_e,s расчет коэффициентов k и β′ цельной крови выполняется по формулам (9) и (10). В предположении, что индикатриса рассеяния крови не зависит от плотности упаковки эритроцитов, очевидно, что g=g_e.

Таким образом, выражения (11)-(16) позволяют в простом аналитическом виде рассчитывать КП тонкой кюветы с цельной кровью в диапазоне λ=450-850 нм с учетом многократного рассеяния света и формы эритроцитов, что является основой для оперативной количественной интерпретации получаемых в эксперименте результатов.

Количественный анализ спектра пропускания крови.

Количественные оценки морфологических и биохимических параметров крови b по данным спектрофотометрических измерений основываются на минимизации невязки между экспериментальным T_mes(λ) и расчетным Т(λ,b) спектрами пропускания кюветы с кровью:

где D и Δλ - используемые диапазон длин волн и спектральное разрешение.

Погрешности определения параметров крови с использованием предлагаемого способа оценивались на основе замкнутых численных экспериментов, суть которых поясняется фиг.5. Спектр T_meas(λ), используемый для нахождения параметров крови (модельных параметров), изображен на фиг.5 точками. Данный спектр получен как Т_МС(λ)+δТ(λ), где Т_МС(λ) - спектр пропускания крови, рассчитанный методом Монте-Карло при заданных значениях модельных параметров (V_e=90 мкм³, p_e=3.0, МСНС=340 г/л, H=0.4, S=0.8, c_COHb=0.05, c_MetHb=0.05, c_SHb=0.05, C_bil=50 мг/л); δT(λ) - случайные флуктуации в пределах 2% от Т_МС(λ), моделирующие погрешности фотометрических измерений. Спектр Т(λ,b) рассчитывался с использованием полученных аналитических выражений (11)-(16). Минимизация невязки (17) выполнялась методом Левенберга-Марквардта [27]. Аналитический спектр Т(λ,b), соответствующий минимуму невязки (17) (σ≈0.005), изображен на фиг.5 сплошной кривой. Данному спектру соответствуют следующие значения модельных параметров: V_e=93 мкм³, p_e=3.7, МСНС=336 г/л, H=0.4, S=0.81, c_COHb=0.047, c_MetHb=0.048, c_SHb=0.006, C_bil=49 мг/л.

Сравнивая заданные b и восстановленные b∗ значения модельных параметров, можно оценить погрешности восстановления параметров крови. Аналогичные численные эксперименты проводились для 750 реализации b и T_mes(λ), на основании чего оценены средние погрешности δb восстановления параметров крови и коэффициент корреляции ρ между b и b∗. Значения этих характеристик, соответствующие максимально широкой вариации параметров крови и погрешности фотометрических измерений ~2%, приведены в табл.2.

Табл.2.
Средние погрешности δb восстановления модельных параметров b и коэффициент корреляции ρ между заданными и восстановленными значениями параметров b
b	δb, %	ρ
cHb	2.3	0.9998
c H b O 2	0.8	0.9997
cCOHb	5.4	0.9993
cMetHb	3.9	0.9997
cSHb	3.3	0.9997
Cbil	3.8	0.9996
CtHb	0.7	0.9987
H	1.3	0.9974

Как видно из представленных результатов, заявляемый способ позволяет оперативно и с высокой точностью определять концентрации производных гемоглобина в крови, а также концентрацию билирубина и гематокрит крови. При этом не требуется предварительная обработка крови и использование дополнительных операций, присутствующих в большинстве известных методов анализа крови (например, разбавление, гемолиз, центрифугирование, сферизация эритроцитов и т.д.). Расширяются функциональные возможностей за счет одновременного определения всех производных гемоглобина (оксигемоглобина, дезоксигемоглобина, карбоксигемоглобина, метгемоглобина, сульфгемоглобина), а также гематокрита и концентрации билирубина в крови.

Литература

1. Патент США №5318122, МПК A61B 5/00, 6/00, 07.06.1994.

2. Авт. св. СССР №1613955, G01N 33/49, 15.12.1990.

3. Патент РФ №2140083, G01N 33/52, G01N 33/72, 20.10.1999.

4. Single scattering by red blood cells / M. Hammer [et. al.] // Appl. Opt. 1998. V.37, №31. P.7410-7418.

5. Кириллин, М.Ю. Моделирование распространения лазерного пучка в плоском слое суспензии эритроцитов методом Монте-Карло: сравнение вкладов рассеяния с различными кратностями в угловое распределение света / М.Ю. Кириллин, А.В. Приезжев // Квантовая электроника. 2002. Т.32, №10. С.883-887.

6. Faber, D.J. Oxygen saturation-dependent absorption and scattering of blood / D.J. Faber [et. al.] // Phys. Rev. Let. 2004. V.94, №2. P.028102-1-028102-4.

7. Башкатов, А.Н. Иммерсионное просветление крови человека в видимом и ближнем ИК спектральных диапазонах / А.Н. Башкатов [и др.] // Оптика и спектр. 2005. Т.98, №4. С.695-703.

8. Mroczka, J. Modeling of light transmittance measurement in a finite layer of whole blood - a collimatwd transmittance problem in Monte Carlo simulation and diffusion model / J. Mroczka, R. Szczepanowski // Optica Applicata. 2005. V. XXXV, №2. P.311-331.

9. Clancy, N.Т. Effect of glucose on the optical properties of arterial blood using Mie theory simulations / N.T. Clancy, M.J. Leahy // Diagnostic Optical Spectroscopy in Biomedicine III, edited by Mary-Ann Mycek, Proc. of SPIE-OSA Biomedical Optics. 2005. SPIE Vol.5862. P.58620Y-1-58620Y-7.

10. Roggan, A. Determination of optical properties of human blood in the spectral range 250 to 1100 nm using Monte Carlo simulations with hematocrit-dependent effective scattering phase functions / A. Roggan, G. Müller, M. Meinke // J. Biomed. Opt. 2006. V.11, №3. P.034021-1-034021-10.

11. Yarynovska I.H., Bilyi A.I. Absorption spectra of sulfhemoglobin derivates of human blood // Proc. of SPIE. 2006. V.6094. P.60940G-1-60940G-6.

12. Suzaki, Н. Noninvasive measurement of total hemoglobin and hemoglobin derivatives using multiwavelength pulse spectrophotometry / Н. Suzaki [et. al.] // Engineering in Medicine and Biology Society 2006. EMBS ′06, 28th Annual International Conference of the IEEE. New York: IEEE, 2006. P.799-802.

13. Костюков, Д.В. Спектральные исследования плазмы и крови новорожденных [Электронный ресурс] / Д.В. Костюков [и др.] // Техномедика, - Режим доступа: http://www. technomedica.com/bib/3-Spectra.pdf. свободный.

14. Барун, В.В. Локализованное поглощение света гемоглобинами суспензии эритроцитов / В.В. Барун, А.П. Иванов // Журн. прикл. спектр. 2009. Т.76, №4. С.516-524

15. Friebel, M. Model function to calculate the refractive index of native hemoglobin in the wavelength range of 250-1100 nm dependent on concentration / Friebel M., Meinke M. // Appl. Opt. 2006. V.45, №12. P.2838-2842.

16. Zijlstra W.G., Buursma A., Assendelft O.W. Visible and near infrared absorption spectra of human and animal haemoglobin. Utrecht: VSP, 2000. P.150-157.

17. Dubovik, O. Application of spheroid models to account for aerosol particle nonsphericity in remote sensing of desert dust / O. Dubovik [et. al.] // J. Geophys. Res. 2006. V. 111, D11208, doi:10.1029/2005JD006619.

18. Лопатин, В.Н. [и др.]. Методы светорассеяния в анализе дисперсных биологических сред, Москва: ФИЗМАТЛИТ, 2004. С.135-150.

19. Mishcenko, M.I. Travis, L.D. Lacis, A.A. Scattering, absorption, and emission of ligtht by small particles. New York: NASA Goddard Institute for space studies, 2004. P.100-115.

20. Сидько, Ф.Я. Лопатин, В.Н. Парамонов, Л.Е. Поляризационные характеристики взвесей биологических частиц, Новосибирск: Наука, 1990. С.15-20.

21. Roggan, A. Optical properties of circulating human blood in the wavelength range 400-2500 nm / A. Roggan [et. al] // J. Biomed. Opt. 1999. V.4, №1. P.36-46.

22. Meinke, M. Empirical model functions to calculate hematocrit-dependent optical properties of human blood / M.Meinke [et. al.] // Appl. Opt. 2007. V.46, №10. P.1743-1753.

23. Du, H. PhotochemCAD: A Computer-Aided Design and Research Tool in Photochemistry / H. Du [et. al.] // Photochemistry and Photobiology. 1998. V.68, №2. P.141-142.

24. Twersky, V. Absorption and multiple scattering by biological suspensions //J. Opt. Soc. Am. 1970. V.60, №8. P.1084-1093.

25. Wang, L. MCML - Monte Carlo modeling of photon transport in multi-layered tissues / L. Wang, S.L. Jacques, L. Zheng // Computers Methods and Programs in Biomedicine. - 1995. - №47. - P.131-146.

26. Васильев А.В., Мельникова И.Н. Коротковолновое солнечное излучение в атмосфере Земли. Расчеты. Измерения. Интерпретация. СПб.: НИИХ СПбГУ, 2002. С.45-50.

27. Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. Numeric recipes. The art of scientific computing. Third edition, New York: Cambridge University Press, 2007. P.345-352.

Способ определения концентрации производных гемоглобина в крови, основанный на фотометрировании крови на длинах волн видимого диапазона, отличающийся тем, что осуществляют фотометрирование цельной крови в видимом и ближнем ИК-диапазоне длин волн, измеряют спектральные коэффициенты пропускания кюветы с цельной кровью, а количественные значения концентрации основных производных гемоглобина определяют путем минимизации невязки ,где вектор b - определяемые концентрации производных гемоглобина (окси, деокси, карбокси, мет- и сульфгемоглобин), общего гемоглобина, билирубина, а также гематокрит;T_meas(λ), T(λ_i,b) - соответственно экспериментальные и расчетные значения коэффициентов пропускания крови;D - используемый диапазон длин волн,Δλ - используемое спектральное разрешение,D/Δλ - количество длин волн фотометрирования крови; , , ,где r, r^* - соответственно коэффициенты отражения света от кюветы с кровью и внутренних стенок кюветы;Т₀, Т^* - соответственно коэффициенты пропускания кровью коллимированного и диффузного излучения;а средний косинус индикатрисы рассеяния g, транспортный коэффициент рассеяния β′ и коэффициент поглощения k рассчитываются с учетом полученных путем численного моделирования аппроксимационных зависимостей между сечением поглощения и рассеяния C_e,a, , среднего косинуса индикатрисы рассеяния эритроцитов g_e, которые имеют вид: , , ,где ε_tHb - молярный коэффициент поглощения гемоглобина;МСНС - концентрация гемоглобина в эритроците;p_e - параметр формы эритроцита;V_e - средний объем эритроцита,а a, b, …u - численные коэффициенты, рассчитанные заранее методом наименьших квадратов при аппроксимации указанными выше уравнениями статистических данных о множестве смоделированных связей между оптическими характеристиками, оптическими и биофизическими параметрами крови в известных диапазонах разброса последних.