Способ развертывания и закрутки относительно центра масс космической тросовой системы с помощью гравитационных и внутренних сил

Способ развертывания и закрутки относительно центра масс космической тросовой системы с помощью гравитационных и внутренних сил

Иллюстрации

Показать все

Реферат

Изобретение относится к космической технике, преимущественно к космическим тросовым системам (КТС). Изобретение может быть использовано для перевода КТС в режим ее вращения относительно центра масс (космическая «праща») в плоскости орбиты без использования реактивной двигательной установки и, соответственно, без затрат рабочего тела на этот маневр.

Под космической тросовой системой понимаем совокупность из двух космических аппаратов (КА), соединенных длинным тонким тросом. Потенциальные области практического использования КТС предполагают три устойчивых режима движения КТС [1]: стационарный режим (режим гравистабилизации), режим либрационных колебаний и режим ротации. Общим условием реализации устойчивых режимов движения КТС является движение ее центра масс по круговой орбите с натянутым тросом фиксированной длины.

В режиме ротации под действием гравитационных и центробежных сил на КА связки возникает малая искусственная тяжесть. Этот эффект может быть использован для создания комфортных условий для жизни и работы космонавтов, для выращивания в космосе растений, для дозаправки космических аппаратов топливом с удаленного терминала, для проведения медицинских, биологических, технологических и других экспериментов в условиях малой тяжести, уровень которой можно регулировать [1-3].

Вращающиеся КТС могут также использоваться для генерации в токопроводящем тросе переменного электрического тока, для мониторинга физических полей, для выполнения различных орбитальных маневров космических объектов без затрат топлива. Изменяя определенным образом длину троса КТС, можно осуществлять эволюции параметров ее орбиты, а также взаимное маневрирование концевых объектов связки. При отделении КА от быстро вращающейся связки (космическая «праща») можно сообщить КА достаточно большую дополнительную скорость с целью перевода его на высшую или низшую орбиту, спуск на Землю или перевод на траекторию межпланетного полета. С помощью выстроенных определенным образом в космическом пространстве совокупности «пращей», можно организовать постоянно действующий транспортный канал в космическом пространстве [6-8].

Устойчивые режимы движения КТС, указанные выше, имеют интеграл энергии и количественно могут быть ранжированы безразмерной величиной энергии углового движения натянутой связки относительно своего центра масс. По определению В.В.Белецкого [1], интеграл энергии - это безразмерная величина, значение которой определяется начальными условиями углового движения:

h = ϕ ˙ ¯ 2 − 3 cos 2 ϕ = ϕ ˙ ¯ o 2 − 3 cos 2 ϕ o ,

где φ - фаза углового положения линии визирования объектов КТС;

ϕ ˙ ¯ = ϕ ˙ / ω c - приведенная скорость углового движения КТС;

ω c = μ / r c 3 - угловая скорость орбитального движения центра масс КТС;

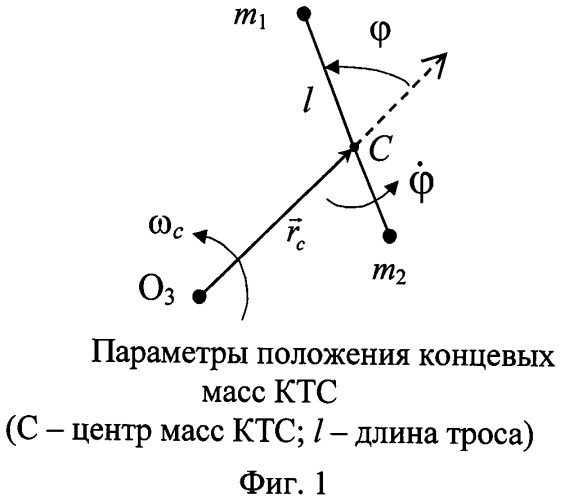
r_с - геоцентрический радиус круговой орбиты центра масс КТС (фиг.1);

µ - константа гравитационного поля Земли.

В режиме гравистабилизации КТС интеграл энергии h_гр=-3.

В режиме либрационных колебаний с амплитудой φ_o∈(0°, 66°) значение интеграла энергии изменяется в диапазоне h_либ=(-3; -0,5).

В режиме попутной ротации значение интеграла энергии h_вр>0.

Перевод КТС в устойчивый режим движения с заданным значением интеграла энергии на тросе заданной длины осуществляют из начального положения, когда два КА, как единое целое, совершают движение по исходной круговой орбите, при этом трос компактно уложен на устройстве подачи-выборки, расположенном на одном из КА.

В техническом аспекте задача перевода КТС в устойчивый режим движения не является тривиальной, поскольку она предполагает одновременное решение двух основных задач:

1) развертывание троса на заданную длину и

2) обеспечение требуемых значений параметров положения и скорости в конце участка развертывания КТС.

Развертывание троса на заданную длину технически может быть реализовано различными способами:

- с помощью импульсного расталкивания - пассивное развертывание;

- с помощью импульсного расталкивания и последующего управления силой натяжения троса - активное развертывание;

- с помощью непрерывной тяги реактивных двигателей, установленных на одном или двух КА связки - активное развертывание;

- с помощью управления комплексированием реактивных сил и упругих сил натяжения троса.

В первых двух вариантах развертывание производится за счет внутренних сил системы.

Обеспечение требуемых терминальных условий в конце участка разведения может быть реализовано:

- подбором начальных условий движения при расталкивании и пассивном развертывании КТС;

- подбором начальных условий движения и параметров программы управления силой натяжения троса в процессе развертывания КТС;

- путем силовой выборки троса и изменения момента инерции углового движения;

- с помощью реактивных двигателей.

В первых трех вариантах перевод КТС в устойчивый режим движения производится за счет внутренних сил системы.

Различные комбинации вариантов управления развертыванием троса и вариантов достижения требуемых терминальных условий определяют различные способы перевода КТС в устойчивые режимы движения.

Рассмотрим известные и исследованные способы развертывания и закрутки космической тросовой системы.

В работах [4, 6] описан и исследован с помощью математических моделей способ развертывания троса и перевода КТС в режим либрационных колебаний [6] и режим ротации [4] с помощью реактивного двигателя, установленного на одном из КА связки. Процесс закрутки КТС выполняется в три этапа:

1. Первое включение двигателя для разведения объектов до некоторого заданного рубежа и предварительной закрутки КТС.

2. Пассивное разведение КА с помощью центробежных сил на заданную длину троса. Относительная скорость в конце участка разведения равна нулю.

3. Второе включение двигателя при фиксированной длине троса для достижения заданных параметров ротации.

Приведены условия, минимизирующие расход рабочего тела на выполнение маневра.

В работе [5] описан и исследован способ «гравитационной закрутки двухсекционного КА» с помощью двух реактивных двигателей, установленных на КА. Процесс закрутки КТС выполняется в три этапа:

1. Включение двигателей для разведения КА и разматывания троса на длину, превышающую требуемое значение. В конце первого этапа КТС переводится в режим либрационного движения из положения максимальной амплитуды.

2. Пассивное либрационное движение КТС до выхода углового положения линии визирования ее концевых объектов в окрестность местной вертикали.

3. Быстрое стягивание КТС в окрестности местной вертикали путем силовой выборки троса для уменьшения момента инерции и перевода КТС в режим ротации.

Исследованы три закона выборки троса: стягивание с постоянной скоростью, выборка троса при постоянной мощности лебедки и стягивание со скоростью, пропорциональной расстоянию между КА. Описанный способ является предпочтительным по критерию расхода рабочего тела.

Достоинством этих способов является принципиальная возможность реализации любых по энергетике режимов ротации КТС произвольной длины. К недостаткам этих способов следует отнести:

- сложность конструктивного исполнения из-за наличия реактивных двигателей и запасов рабочего тела к ним и, как следствие, - низкая надежность;

- исчерпаемость и конечность энергоресурса;

- программы управления движением в обоих способах предполагают наличие нетривиальной системы управления.

Этих недостатков лишена группа способов закрутки, которые основаны на поочередном катапультировании пружинным толкателем с борта массивной орбитальной платформы концевых элементов КТС [2]. Способы различаются начальными условиями катапультирования и условиями подачи троса при развертывании КТС. Способы имеют общие характерные признаки:

1. Перед развертыванием КА закреплены на орбитальной платформе, которая движется по орбите, практически совпадающей с требуемой орбитой центра масс КТС. Трос компактно уложен на устройстве депонирования и подачи, расположенном на одном из КА связки.

2. Оси пружинных толкателей ориентированы в плоскости исходной орбиты. Отделение импульсное за счет внутренних сил системы. Величина импульса скорости отделения - единицы метров за секунду.

3. Массы КА, образующих связку, составляют 1-10 кг, длина троса - порядка 100 метров, угловая скорость вращения системы - 0,1-1,0 с^-1, время развертывания и закрутки системы составляет единицы процентов от периода обращения орбитальной платформы. Достоинством этих способов является простота технической и технологической реализации закрутки КТС в плоскости орбиты, а также возможность многократного запуска с борта орбитальной платформы вращающихся КТС без расхода рабочего тела на проведение маневра.

Основным недостатком этих способов являются существенные массово-габаритные ограничения, накладываемые на КТС.

Предлагаемый способ развертывания и закрутки КТС относительно центра масс с помощью гравитационных и внутренних сил аккумулирует в себе достоинства рассмотренных аналогов и, практически, свободен от перечисленных выше недостатков. Способ не имеет принципиальных ограничений ни по массе КА связки, ни по длине соединительного троса, ни по ресурсозатратам.

Наиболее близким аналогом среди рассмотренных способов закрутки КТС является способ «гравитационной закрутки двухсекционного КА» с помощью двух реактивных двигателей [5], который рассматривается в качестве прототипа. Главным отличием предлагаемого способа закрутки от прототипа является использование внутренних сил системы на первом этапе маневра, что позволяет исключить применение реактивных двигателей. Развертывание КТС в этом случае в плоскости орбиты ее центра масс происходит из начального монолитного состояния системы путем расталкивания объектов с малой начальной относительной скоростью. Концевые массы КТС m_i, i=1, 2 соединены тонким тросом, длина которого может изменяться с помощью устройства подачи-выборки троса. Устройство подачи-выборки может быть установлено на одном из КА связки. В исходном положении до разделения система совершает монолитное движение по круговой орбите радиуса r_с. Разделение объектов производится по линии вектора местной круговой скорости механическим толкателем. Потенциальная энергия толкателя обеспечивает стартовый импульс разделения ΔV. Связанные тросом объекты удаляются друг от друга по свободным траекториям при свободной подаче троса. Процесс развертывания троса завершается переводом КТС в фазовое состояние, из которого она переходит в устойчивый режим попутного маятникового движения на натянутом тросе фиксированной длины.

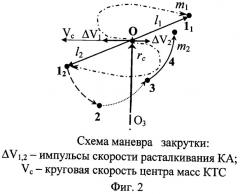
Графически схема маневра закрутки КТС представлена на фигуре 2 в виде годографа векторов концевых масс [9]. Для равновеликих концевых масс связки их траектории относительного движения практически симметричны относительно центра масс. Технологически маневр закрутки КТС можно разделить на несколько этапов:

1 Этап. Точка О на фиг.2, 3 - импульсное трансверсальное разделение объектов КТС на исходной орбите О_с и переход КА на эллиптические орбиты O₁ и О₂.

2 Этап. Участок траектории 0-1 на фиг.2. Пассивное развертывание КТС при свободной подаче троса.

3 Этап. Участок траектории 1₂-2. Попутное маятниковое движение КТС на натянутом тросе фиксированной длины.

4 Этап. Участок траектории 2-3. Стягивание КТС путем силовой выборки троса с постоянной скоростью.

5 Этап. Участок траектории 3-4. Ротация КТС с заданным значением интеграла энергии при фиксированной длине троса.

Предлагаемый способ развертывания и закрутки КТС относительно ее центра масс исследован на математической модели при следующих допущениях:

- движение КТС рассматривается в ньютоновском поле притяжения;

- трос - невесомая, гибкая и нерастяжимая нить из высокомодульного материала;

- при пассивном развертывании КТС (участок 0-1) подача троса с устройства происходит без сопротивления;

- стягивание КТС производится с постоянной скоростью выборки троса.

Исследования проведены в рамках следующей постановки задачи. В исходном состоянии КТС, состоящая из двух КА массой m_i i=1, 2, монолитным блоком движется по круговой орбите с геоцентрическим радиусом r_с. Соединительный трос уложен на устройстве подачи-выборки, которое установлено на одном из КА. Устройство позволяет реализовать свободную подачу троса при удалении КА друг относительно друга после их расталкивания, а также производить силовую выборку троса с постоянной скоростью сматывания а=const. Расталкивание КА производится по линии вектора орбитальной скорости с помощью пружинного толкателя, реализующего стартовый импульс скорости разделения ΔV. Максимальные значения скорости сматывания троса и импульса скорости расталкивания КА имеют одинаковый порядок и не превышают 10 м/с.

Необходимо определить величину импульса расталкивания, параметры траектории пассивного развертывания, маятникового движения и силовой выборки троса со скоростью, позволяющей перевести КТС из исходного состояния в режим ротации с заданной величиной интеграла энергии h_вр>0 при заданной длине троса.

Решение задачи с целью обобщения ее результатов представляется в безразмерных параметрах и переменных:

- m ¯ = m 2 / m 1 - соотношение масс концевых элементов КТС;

- Δ V ¯ = Δ V / V C - безразмерный импульс расталкивания, где V C = μ / r C - круговая скорость центра масс КТС;

- l ¯ = l / r C - относительная длина троса.

1 этап. Для определенности полагаем, что при расталкивании КА массой m₁ получил разгонный импульс скорости ΔV₁, а КА массой m₂ - тормозной импульс ΔV₂. На основе аддитивности импульса (количества движения) - «импульс системы равен сумме импульсов ее отдельных частиц вне зависимости от возможности пренебрежения взаимодействием между ними» [10] - с учетом ограничений на потенциал толкателя ΔV₁+ΔV₂=ΔV, получим импульсы скорости расталкивания:

Δ V ¯ 1 = m ¯ m ¯ + 1 Δ V ¯ ,          Δ V ¯ 2 = 1 m ¯ + 1 Δ V ¯ .                             (2)

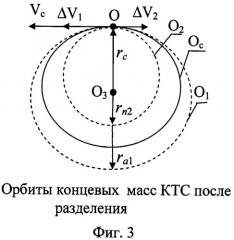
Расчет движения по эллиптическим орбитам O₁ и О₂ (фиг.3), геометрические параметры которых зависят от импульсов скорости расталкивания:

p ¯ 1 = p 1 r C = ( 1 + m ¯ m ¯ + 1 ⋅ Δ V ¯ ) 2 ,             e 1 = p ¯ 1 − 1 ;

p ¯ 2 = p 2 r C = ( 1 − 1 m ¯ + 1 ⋅ Δ V ¯ ) 2 ,             e 2 = 1 − p ¯ 2 .

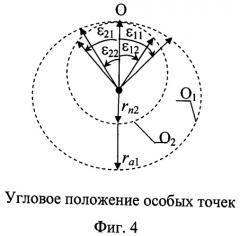
Относительное и абсолютное движение концевых масс по этим траекториям подробно рассмотрено в монографии [9]. Установлено, что на этих траекториях существуют две особые точки, в которых скорость относительного движения концевых масс равна нулю, а ускорения имеют противоположные знаки. Эти особые точки являются границами реверсного относительного движения КА. Угловое положение особых точек не зависит от массового соотношения объектов КТС и величины импульса скорости расталкивания в диапазоне значений ΔV<30 м/с. Эти точки расположены на эллиптических орбитах (фиг.4) практически симметрично относительно точки О разделения КТС на стартовой орбите.

Угловое положение первой особой точки: ε₁₁=42,5⁰ (истинная аномалия ϑ₁₁=317,5°) и ε₁₂=41° (ϑ₁₂=139°). Время прибытия концевых тел в эту точку, выраженное в единицах периода обращения орбиты центра масс, равно t ¯ р е в =0,886. Расстояние между концевыми телами l ¯ р е в = 19 , 32 ⋅ Δ V ¯ . В первой особой точке начинается реверсный режим движения КТС и связанная с этим необходимость выборки свободного троса. Этот процесс завершается во второй особой точке, при этом параметры относительного движения КТС удовлетворяют условиям безударного перевода КТС в режим попутного колебательного движения. На фиг.2 вторая особая точка обозначена символами «l₁» и «l₂». Угловое положение второй особой точки:

ε21=ϑ₂₁=40,5° и ε₂₂=41° (ϑ₂₂=221°). Время прибытия в точку t ¯ 1 ≈ 1 , 113 . Расстояние между концевыми телами l ¯ 1 = 18 , 4 ⋅ Δ V ¯ . Если зафиксировать эту длину, то система перейдет в режим попутного маятникового движения с начальными условиями:

,

и значением интеграла энергии:

h 1 = ϕ ˙ ¯ 1 2 − 3 cos 2 ϕ 1 = 0 , 003.                                 (5)

Это значение интеграла энергии близко к нулю и соответствует переходному состоянию между либрационным и ротационным движениями КТС.

2 этап. Попутное маятниковое движение КТС на натянутом тросе описывается уравнениями [9]:

ϕ ¨ ¯ + 2 a / l ¯ ( ϕ ˙ ¯ + 1 ) + 3 sin ϕ cos ϕ = 0 ,

n C = ( ϕ ˙ ¯ + 1 ) 2 − 1 + 3 cos 2 ϕ ,

где n_с - местная перегрузка от силы натяжения троса F n = m 1 m 2 / ( m 1 + m 2 ) ⋅ l ⋅ ω c 2 ⋅ n c .

Если зафиксировать длину троса, то угловое движение КТС на интервале φ∈(φ₁, φ₂) можно описать уравнением ϕ ¨ ¯ + 3 sin ϕ ⋅ cos ϕ = 0 .

Время движения КТС на этом этапе определяется угловой фазой начального и конечного состояний [9]:

t ¯ 12 = 1 2 π 3 ⋅ ln ( 1 + sin ϕ 1 1 + sin ϕ 2 ⋅ cos ϕ 2 cos ϕ 1 ) .

3 Этап. Стягивание КТС с постоянной скоростью. Конечное состояние системы после ее стягивания до заданного уровня энергии ротации h_вр однозначно определяется фазовым углом φ₃, остаточной длиной троса l₃ и приращением безразмерной энергии вращения Δh. В соответствии с [1], параметры конечного состояния КТС определяются с помощью интеграла энергии:

ϕ ˙ ¯ 3 2 − 3 cos 2 ϕ 3 = ϕ ˙ ¯ 2 2 − 3 cos 2 ϕ 2 + Δ h .

Возникает задача достижения конечного состояния за минимальное время стягивания. Минимизация времени стягивания при постоянной скорости выборки троса адекватна задаче максимизации кинетического момента вращения КТС. Стягивание КТС производится путем силовой выборки троса. Программа управления стягиванием в виде скорости выборки троса a=const в угловом секторе φ₂<φ<φ₃ определяет приращение энергии ротации на величину Δh. Переходная траектория описывается системой уравнений:

d ϕ d ϕ = 1 ; ϕ ˙ ¯ d l ¯ d ϕ = − a ; ϕ ˙ ¯ d ϕ ˙ ¯ d ϕ = 2 a ϕ ˙ ¯ + 1 l ¯ − 3 sin ϕ ⋅ cos ϕ .

Приходим к задаче оптимального управления с двумя подвижными концами: определить оптимальную программу стягивания КТС

а(φ) для φ₂<φ<φ₃ и соответствующую ей переходную траекторию, которая переводит систему из начального состояния

в конечное

ϕ ˙ ¯ 2 ( ϕ 3 ) − 3 cos 2 ϕ 3 − Δ h = 0

при минимальной длине выбранного троса

Δ l ¯ = l ¯ ( ϕ 2 ) − l ¯ ( ϕ 3 ) = ∫ ϕ 2 ϕ 3 a ϕ ˙ ¯ d ϕ .

Гамильтониан этой системы

H = u ¯ ϕ ˙ ¯ + Ψ 1 − Ψ 2 u ¯ ϕ ˙ ¯ + Ψ 3 ( 2 a ϕ ˙ ¯ ⋅ ϕ ˙ ¯ + 1 l ¯ − 3 ϕ ˙ ¯ sin ϕ ⋅ cos ϕ )

линейно зависит от управления. Это означает, что оптимальное управление является релейной функцией:

a=const≠0 при φ∈(φ₂, φ₃); а=0 при φ∉(φ₂, φ₃),

а задача оптимального управления при этом превращается в задачу на быстродействие с поиском границ углового сектора (φ₂, φ₃) по знаку функции переключения.

Используя условия трансверсальности и необходимые условия экстремума в виде:

H * = max ︸ u H ( Ψ * , x * , a ) ; H * ( ϕ 2 ) = H * ( ϕ 3 ) = 0 ,

можно решить краевую задачу для уравнения

Δ h = 4 a ∫ ϕ 2 ϕ 3 ϕ ˙ ¯ ( ϕ ) + 1 l ¯ d ϕ = − 4 ∫ l ¯ 1 l ¯ 3 ϕ ˙ ¯ ⋅ ( ϕ ˙ ¯ + 1 ) l ¯ d l ¯ .

Этот интеграл можно приближенно вычислить при условиях, позволяющих применить теорему о среднем:

Δ h = A ( ln l ¯ 1 − ln l ¯ 3 ) = A ⋅ ln l ¯ 1 l ¯ 1 − Δ l ¯ ,

где A = 4 ϕ ˙ ¯ с р ( ϕ ˙ ¯ с р + 1 ) ; ϕ ˙ ¯ с р = 1 2 ( ϕ ˙ ¯ 2 + ϕ ˙ ¯ 3 ) ;

ϕ ˙ ¯ 2 = 3 cos 2 ϕ 2 ; ϕ ˙ ¯ 3 = 3 cos 2 ( ϕ 2 + Δ ϕ ) + Δ h .

Полученное выражение устанавливает связь между изменением энергии ротационного движения Δh и ресурсными затратами на маневр в виде выбранной длины троса Δ l ¯ . Как видно из этих соотношений, ресурсные затраты зависят от начальной φ₂ и конечной фазы выборки троса φ₃=φ₂+Δφ. Это позволяет исходную задачу оптимального управления свести к задаче поиска экстремума параметрической функции ресурсных затрат:

ϕ 2 = arg min ϕ 2 ∈ ( ϕ 1 ; − ϕ 1 ) { Δ l ¯ ( ϕ 2 ; Δ ϕ ) } ,

где критериальная функция

Δ l ¯ = l ¯ 1 − l ¯ 3 = l ¯ 1 ( 1 − exp ( − Δ h / A ) )

и исследуется на экстремум. Необходимое условие экстремума дает уравнение

ϕ ˙ ¯ 3 ⋅ cos ϕ 2 sin ϕ 2 + ϕ ˙ ¯ 2 ⋅ cos ( ϕ 2 + Δ ϕ ) sin ( ϕ 2 + Δ ϕ ) = 0 ,

решение которого определяет аргумент экстремума:

ϕ 2 = π − 1 2 arctan sin 2 Δ ϕ B ( Δ ϕ ) + cos 2 Δ ϕ ,       B( Δ ϕ ) = 1 + Δ h 3cos 2 Δ ϕ 2 .

При Δh→0 слагаемое B(Δφ)→1 и φ₂≈π-0,5·Δφ, то есть угловой сектор области стягивания КТС симметричен относительно местной вертикали центра масс в окрестности зенита и надира. С увеличением значения параметра Δh симметрия нарушается и сектор совершает попутное смещение.

Порядок решения задачи перевода КТС в режим ротации:

- задают исходные данные: r_с, ΔV, Δh, Δφ;

- вычисляют вспомогательные параметры: Δ V ¯ = Δ V / V c , V c = μ / r c , ω c = μ / r c 3 , T c = 2 π / ω c ;

- определяют параметры движения КТС в конце развертывания:

φ₁=91,5°, ϕ ˙ ¯ 1 = 0 , 071 , l ¯ 1 = 18 , 4 ⋅ Δ V ¯ ;

- определяют границы области свертывания КТС φ∈(φ₂, φ₂+Δφ);

- определяют средние значения параметров ϕ ˙ ¯ с р и А;

- вычисляют параметры, характеризующие процесс закрутки КТС:

1. Относительная длина выбранного троса Δ l ¯ = l ¯ 1 ( 1 − exp ( − Δ h / A ) ) .

2. Доля выбранного троса после стягивания КТС: J = Δ l ¯ / l ¯ 1 = 1 − exp ( − Δ h / A ) .

3. Удельная доля выбранного троса J_h=J/Δh.

4. Время выборки троса Δ t ¯ = Δ ϕ 2 π ⋅ ϕ ˙ ¯ с р .

5. Относительная скорость выборки троса a = Δ l ¯ Δ ϕ ϕ ˙ ¯ с р .

6. Время окончания маневра:

t ¯ 3 = 1 , 114 + 1 2 π 3 ln ( − 1 + sin ϕ 1 1 + sin Δ ϕ / 2 ⋅ cos Δ ϕ / 2 cos ϕ 1 ) + Δ ϕ 2 π ϕ ˙ ¯ с р .

Отсчет времени производится от момента расталкивания объектов на стартовой орбите. Приближенная оценка времени маневра составляет полтора периода обращения по орбите ц