Способ измерения резонансной частоты

Способ измерения резонансной частоты

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может быть использовано для высокоточного определения резонансной частоты электромагнитных резонаторов, а также величин, которые функционально связаны с резонансной частотой резонаторов, входящих в состав радиочастотных датчиков и применяемых в различных областях техники и научных исследованиях. В частности оно может быть использовано в радиочастотных резонансных датчиках влагосодержания нефтепродуктов, концентрации растворов и резонансных уровнемерах различных сред.

Известны различные способы измерения резонансной частоты. Широкое применение получил способ, реализованный в устройстве (SU 1758510 А1, 30.08.1992), которое выполнено на базе экстремального регулятора. В этом устройстве высокочастотный генератор, управляемый напряжением (ГУН), автоматически настраивается на резонансную частоту радиочастотного датчика и отслеживает все ее изменения. При этом частота высокочастотного генератора осциллирует около максимума амплитудно-частотной характеристики (АЧХ) этого датчика и усредненное значение этой частоты считается резонансной частотой этого датчика. Указанный способ имеет следующие недостатки:

1) АЧХ резонатора должна быть только с одним максимумом, так как при наличии других локальных максимумов возможно ложное срабатывание и захват локального максимума вместо основного;

2) поскольку резонансная частота определяется как среднее значение осциллирующей частоты ГУН, то для получения точного значения резонансной частоты необходимо измерять частоту ГУН в течение длительного времени;

3) при измерении резонансной частоты с использованием перестраиваемых генераторов на выходе резонатора наблюдается динамическая резонансная кривая, максимум которой сдвинут относительно максимума статической резонансной кривой, что приводит к дополнительной погрешности измерения резонансной частоты. Этот сдвиг объясняется наличием переходного процесса в резонаторе при перестройке частоты возбуждения и величина этого сдвига s определяется по формуле (Харкевич А. А. Спектры и анализ. М.: Государственное издательство технико-теоретической литературы. 1957)

s = 8 λ / ( ω r 2 d 2 ) ,

где λ - скорость изменения частоты генератора;

ω_r - резонансная частота;

d - затухание резонатора.

Наиболее близким к предлагаемому способу по технической сущности является способ измерения резонансной частоты, описанный в устройстве (RU 2427805 С1, 27.08.2011) и принятый в качестве прототипа. Согласно этому способу с помощью синтезатора частоты, управляемого микропроцессором, в резонаторе (радиочастотном датчике) последовательно возбуждают колебания различных частот из заданного диапазона. На выходе резонатора амплитуда этих колебаний преобразуется в цифровую форму с помощью аналого-цифрового преобразователя (АЦП) и затем эта амплитуда и соответствующая ей частота фиксируются с помощью микропроцессора. После этого микропроцессор определяет максимум напряжения на выходе резонатора и соответствующую этому максимуму частоту, которую принимают равной резонансной частоте.

Недостатком способа-прототипа, реализованного в указанном устройстве, является наличие существенной погрешности измерения резонансной частоты, обусловленной как дискретностью перестройки частоты синтезатора, так и влиянием помех, вызванных переходными процессами при возбуждении резонатора серией радиоимпульсов, каковыми, по сути, являются сигналы на выходе синтезатора.

В результате этого на огибающую сигнала на выходе резонатора накладываются колебания с частотой Ω, являющиеся результатом сложения затухающих собственных колебаний резонатора с частотой ω₀ и колебаний синтезатора с частотой ω_i.

Ω = | ω 0 − ω i | .   ( 1 )

Эти колебания искажают форму получаемой таким способом АЧХ, и поэтому максимум этой АЧХ не соответствует резонансной частоте.

Задачей настоящего изобретения является расширение арсенала технических средств.

Техническим результатом изобретения является уменьшение погрешности измерения резонансной частоты, обусловленной дискретностью частот возбуждения и влиянием переходных процессов и случайных помех, а также уменьшение времени измерения указанной резонансной частоты без ухудшения точности измерения.

Технический результат достигается тем, что предлагаемый способ измерения резонансной частоты, основанный на последовательном возбуждении в резонаторе колебаний различных частот из заданного набора и фиксирования этих частот и соответствующих им значений амплитуды выходного сигнала резонатора, отличается тем, что для каждой из частот возбуждения фиксируют амплитуду выходного сигнала после затухания переходного процесса в резонаторе, аппроксимируют полученную дискретную зависимость амплитуды от частоты непрерывной функцией и резонансную частоту резонатора определяют по максимуму этой функции.

Предлагаемое изобретение поясняется следующими рисунками.

Фиг.1 - вид сигналов в характерных точках схемы, реализующей предлагаемый способ, где 1 - зависимость частоты выходного сигнала синтезатора ω_i от времени t (фиг.1а); 2 - сигнал на выходе детектора, получаемый при дискретном изменении частоты возбуждения (дискретная АЧХ); 3 - график функции, аппроксимирующей полученную дискретную АЧХ резонатора (фиг.1б).

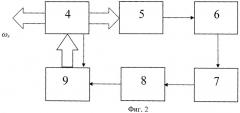
Фиг.2 - структурная схема устройства, реализующего предлагаемый способ, где 4 - цифровой сигнальный процессор (ЦСП), 5 - синтезатор частоты, 6 - фильтр низких частот (ФНЧ), 7 - резонатор, 8 - детектор, 9 - аналого-цифровой преобразователь (АЦП).

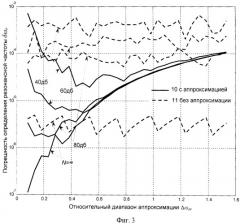
Фиг.3 - экспериментальные кривые зависимости погрешности определения резонансной частоты от относительного диапазона частот, в котором производится аппроксимация, для различных способов определения резонансной частоты (кривые 10 - аппроксимация дискретной АЧХ полиномом 4-ой степени и определение резонансной частоты по максимуму полинома и кривые 11 - определение резонансной частоты непосредственно по максимуму дискретной АЧХ) и для различных значений отношения сигнал/шум N.

Фиг.4 - вид сигнала с шумами на выходе детектора (кривая 12) и полинома 4-ой степени, аппроксимирующего этот сигнал (кривая 13).

Сущность предлагаемого изобретения заключается в том, что заданный диапазон измерения резонансной частоты разбивают на N интервалов, каждому из которых соответствует частота ω_i. Сигнал с частотой ω_i - в момент времени t_i подается на резонатор. Откликом этого резонатора будет сигнал u(t), который, как показано в (Харкевич А.А. Основы радиотехники. М.: Государственное издательство литературы по вопросам связи и радио. 1962), имеет вид

u ( t − t i ) ≈ U m ε i 2 + d 2 [ sin ( ω i ( t − t i ) + ϕ ) − e − α ( t − t i ) sin ( ω 0 ( t − t i ) + ϕ ) ] ,   ( 2 )

где ε i = 1 − ω i 2 / ω 0 2 - относительная расстройка;

α=dω₀/2- постоянная затухания резонатора;

U_m - амплитуда сигнала на входе резонатора;

t - текущее время;

φ - начальная фаза;

d - затухание резонатора;

ω₀ - собственная частота резонатора.

Огибающая этого сигнала на выходе резонатора U_i(t-t_i) выражается формулой

u ( t − t i ) ≈ U m ε i 2 + d 2 1 + e − α ( t − t i ) − 2 e − α ( t − t i ) cos ( Ω ( t − t i ) ) ,   ( 3 )

Из выражения (3) может быть получена формула для длительности переходного процесса в резонаторе τ при условии, что

е^-ατ=0,1.

Отсюда

τ = 2 , 3 / α = 4 , 6 L / r = 4 , 6 Q / ω 0 = 4 , 6 / ( ω 0 d )   ( 4 )

Из вышесказанного вытекает, что при подаче на вход резонатора синусоидального сигнала 1 со ступенчато изменяющейся частотой (фиг.1а) сигнал 2 на выходе резонатора после детектирования будет выглядеть как ступенчатая функция времени t, на горизонтальные участки которой накладываются затухающие колебания, описываемые формулой (3) (фиг.1б).

Из фиг.1б видно, что, применяя дискретное возбуждение резонатора в моменты времени t_i сигналом с частотой ω_i - необходимо учитывать наличие переходных процессов, возникающих в каждый из моментов t_i. Поэтому для получения более точных значений дискретной АЧХ авторами предлагается проводить измерение амплитуды сигнала U_i на выходе резонатора в интервале Δt_i только после затухания переходного процесса, вызванного воздействием на резонатор единичного колебания с частотой ω_i. В этом случае величина интервала Δt_i должна быть не меньше суммы длительности переходного процесса в резонаторе τ и длительности цифровой обработки аналогового сигнала, снимаемого с выхода резонатора, τ_р.

Δ t i ≥ τ + τ p .   ( 5 )

В этом случае величина минимального шага перестройки частоты возбуждающего сигнала Δω_s может быть вычислена по формуле

Δ ω s ≥ ( ω max − ω min ) Δ t i / t s k   ( 6 ) ,

где ω_max, ω_min - границы диапазона резонансных частот исследуемого резонатора;

t_sk - длительность сканирования заданного диапазона резонансных частот;

Δt_i - - интервал времени, в течение которого производится возбуждение резонатора единичным колебанием с частотой ω_i.

Чтобы уменьшить погрешность измерения резонансной частоты, обусловленную конечным значением шага перестройки Δω_s и наличием переходных процессов в резонаторе, в изобретении предлагается аппроксимировать дискретную АЧХ резонатора непрерывной функцией. В качестве такой функции могут быть взяты различные аналитические зависимости, широко применяемые для сглаживания экспериментальных данных, например, полином n-ой степени, сплайны, уравнение резонансной кривой и т.д. Рекомендации по выбору вида аппроксимирующей функции сводятся к следующему.

Если аналитическое выражение для АЧХ исследуемого резонатора известно, то в качестве аппроксимирующей функции следует выбрать такое выражение, которое наиболее точно описывает указанную АЧХ, например, уравнение резонансной кривой, в обратном случае следует предпочесть полиномы или сплайны.

Использование полиномов и сплайнов облегчается тем, что для них уже разработаны и доступны различные компьютерные программы аппроксимации. Если, например, для аппроксимации используется полином n-ой степени, то для определения коэффициентов этого полинома необходимо решить систему из n линейных уравнений. Очевидно, что эти уравнения можно получить, имея всего n пар значений U₁, ω_I, однако на практике для наиболее точной аппроксимации необходимо использовать максимально возможное количество пар U_i, ω_i, или учитывая конечное значение шага перестройки Δω_i, увеличивать диапазон частот, в котором производится обработка величин A_i, ω_i. Это обусловлено тем, что на огибающую сигнала на выходе резонатора накладываются различного типа шумы и наводки. Поэтому обработка максимального количества пар A_i, ω_i, например, по методу наименьших квадратов приводит к сглаживанию этой огибающей, что в итоге уменьшает влияние этих шумов и наводок. Это можно объяснить также тем, что применение метода наименьших квадратов при аппроксимации АЧХ резонатора и последующем определении резонансной частоты эквивалентно усреднению данных измерения резонансной частоты. Однако при этом необходимо иметь в виду, что любая аппроксимация наиболее точно описывает АЧХ резонатора только в узкой полосе частот, центральная частота которой совпадает с резонансной частотой, и при увеличении этой полосы увеличивается также и погрешность аппроксимации. Кроме этого, увеличение диапазона аппроксимации приводит к уменьшению отношения сигнал/шум на выходе резонатора. Поэтому существует оптимальное значение полосы частот, при котором суммарная погрешность, то есть погрешность, обусловленная влиянием шумов, плюс погрешность аппроксимации сводится к минимуму. Это оптимальное значение, как показали исследования, зависит от добротности резонатора, уровня шумов, шага перестройки частоты, степени аппроксимирующего полинома, но всегда находится в пределах полосы пропускания резонатора Δω, определенной на уровне 0,707 (Δω=ω₀/Q), что демонстрируют кривые 11 зависимости погрешности определения резонансной частоты от относительного диапазона частот аппроксимации, представленные на фиг.3.

Следует отметить, что существует также оптимальное значение степени аппроксимирующего полинома, при которой погрешность определения резонансной частоты минимальная, и это значение находится в пределах 3÷5. Это обусловлено тем, что хотя для получения высокой точности аппроксимации необходимо максимально увеличивать степень полинома и соответственно требуемое количество уравнений, однако при этом уменьшается количество независимых систем, которые можно составить из этих уравнений, что приводит к снижению эффективности усреднения.

Алгоритм определения резонансной частоты при аппроксимации дискретной АЧХ резонатора непрерывной функцией в общем случае заключается в следующем.

Используя зафиксированные пары значений U_i, ω_i, по методу наименьших квадратов определяются параметры аппроксимирующей функции (для полинома это коэффициенты полинома n-ой степени P(ω); для уравнения резонансной кривой это собственная частота ω₀ и затухание d. Далее численными методами находится максимум этого полинома и соответствующая этому максимуму частота, которая принимается равной резонансной частоте, либо аналитическим методом находятся корни уравнения P'(ω)=0, один из которых принимается равным резонансной частоте. При использовании в качестве аппроксимирующей функции уравнения резонансной кривой резонансная частота ω_r определяется по известной формуле

ω r = ω 0 ( 1 − d 2 / 2 ) .

Поскольку при любой аппроксимации уже в пределах одноразового сканирования обрабатывается максимальное количество пар значений U_i, ω_i, то время измерения без ухудшения точности можно сократить до длительности этого сканирования t_sk, что также является существенным преимуществом предлагаемого способа.

Предлагаемый способ может быть реализован по схеме устройства, представленной на фиг.2.

Указанное устройство работает следующим образом. ЦСП 4 формирует интервалы дискретизации Δt_i и соответствующие коды для управления частотой синтезатора 5 и АЦП 9. Эти коды периодически через интервалы Δt_i подаются на вход синтезатора 5 и по ступенчатому закону изменяют его частоту в диапазоне изменения резонансных частот (фиг.1а). Одновременно эти коды запоминаются ЦСП 4. От ЦСП 4 также поступают коды на управляющий вход АЦП для получения выборок в определенные моменты времени, соответствующие установившемуся режиму в исследуемом резонаторе. Далее высокочастотный сигнал с выхода синтезатора 5 с частотой ω_i поступает на вход ФНЧ 6, который предназначен для подавления гармоник и других составляющих спектра, присутствующих в выходном сигнале синтезатора 5. С выхода ФНЧ 6 высокочастотный сигнал поступает на вход исследуемого резонатора 7 и затем на детектор 8, который выделяет напряжение огибающей этого высокочастотного сигнала U_i (фиг.1б, кривая 2). Напряжение U_i поступает на вход АЦП 9 и в заданные моменты времени преобразуется в цифровой код. От АЦП 9 коды выборок напряжения U_i поступают на ЦСП 4, где накапливаются вместе с соответствующими кодами частот ω_i. По окончании сканирования ЦСП 4 производит логические и вычислительные операции, связанные с выделением значений U_i, ω_i, которые находятся в пределах оптимального частотного диапазона, вычислением коэффициентов аппроксимирующего полинома (или параметров ω₀ и d) и определения резонансной частоты ω₀ по выбранному алгоритму.

Эффективность предлагаемого способа была подтверждена экспериментом с виртуальной моделью резонатора, дискретная АЧХ которого описывается следующим выражением

A i = 1 / ( 1 − ( ω i / ω 0 ) 2 ) 2 + d 2 ω i 2 / ω 0 2 .   ( 7 )

Точное значение резонансной частоты ω_rs для данной модели резонатора вычисляется по формуле

ω r s = ω 0 ( 1 − d 2 / 2 ) ,

и это значение было принято за эталон.

Модель была выполнена в среде Matlab и имела следующие параметры: ω₀=3·10⁸ рад/сек; ω_max=1,2·10⁸ рад/сек; ω_min=0,8·10⁸ рад/сек. Время сканирования t_sk=100 мсек. Для добротности, изменяющейся в интервале Q=20÷100, минимальный шаг перестройки частоты синтезатора с учетом формул (4) (5) и (6) Δω_s=10³ рад/сек. Для приведенных данных по формуле (7) была рассчитана дискретная АЧХ, на которую для имитации помех была наложена случайная функция типа Гауссова шума. На фиг.4 представлены вид этой дискретной АЧХ при отношении сигнал/шум N=80дБ и Q=20 (кривая 12) и результаты аппроксимации этой дискретной АЧХ полиномом 4-ой степени для относительного диапазона аппроксимации Δω_ar=0,3 (кривая 13), который определялся как

Δω_ar=Δω_a/Δω,

где Δω_a - диапазон частот, в котором производилась аппроксимация дискретной АЧХ;

Δω - полоса частот пропускания исследуемого резонатора.

При исследовании влияния относительного диапазона аппроксимации на погрешность определения резонансной частоты отношение сигнал/шум варьировалось в интервале N=40дБ÷∞. Резонансная частота определялась для Q=20 следующими методами:

1) Предложенным авторами способом определения резонансной частоты по максимуму полинома 4-ой степени, аппроксимирующему дискретную АЧХ с помехами.

2) Способом определения резонансной частоты непосредственно по максимуму дискретной АЧХ с помехами (как в прототипе).

Затем используя полученные экспериментальные значения резонансной частоты ω_re и эталонное значение ω_rs, рассчитанное по формуле (8), для каждого из способов определялась относительная погрешность определения резонансной частоты ω_r в соответствии с формулой

δω_r =(ω_re-ω_rs)/ω_rs.

На фиг.3 представлены графики зависимости погрешности δω_r от относительного диапазона аппроксимации Δω_ar при использовании предлагаемого способа (семейство кривых 10) и при использовании способа-прототипа (семейство кривых 11).

Результаты эксперимента, представленные на фиг.3, наглядно показывают, что погрешность способа, предложенного авторами, как минимум на порядок меньше погрешности способа-прототипа в широком диапазоне отношений сигнал/шум.

Способ измерения резонансной частоты, характеризующийся тем, что последовательно возбуждают в резонаторе колебания различных частот из заданного набора и фиксируют эти частоты и соответствующие им значения амплитуды выходного сигнала резонатора, отличающийся тем, что для каждой из частот возбуждения фиксируют амплитуду выходного сигнала после затухания переходного процесса в резонаторе, аппроксимируют полученную дискретную зависимость амплитуды от частоты непрерывной функцией и резонансную частоту резонатора определяют по максимуму этой функции.