Способ определения статического и динамического коэффициентов внешнего трения

Способ определения статического и динамического коэффициентов внешнего трения

Иллюстрации

Показать все

Реферат

Изобретение относится к области механических испытаний материалов, в частности, к определению статического и динамического коэффициентов трения.

Известны различные способы определения статического и динамического коэффициентов внешнего трения. В большинстве случаев для определения статического и динамического коэффициентов внешнего трения требуется не только проведение отдельных опытов, но и использование различных устройств. Например, известен способ, применяемый для определения только статического коэффициента внешнего трения, состоящий в изменении угла наклона φ относительно горизонта двух образцов, расположенных один на другом, и измерении угла φ в момент, когда начинается скольжение одного образца относительно другого, с расчетом коэффициента m внешнего трения по формуле m=tgφ [патент США №3020744, кл. 73-9, кл. G01N 19/02, 1962]. Для определения динамического коэффициента внешнего трения используются другие устройства, основанные на непосредственном измерении силы трения при известной или измеряемой силе прижатия образцов друг к другу. Использование таких устройств для определения статического коэффициента внешнего трения, как правило, также невозможно.

Известен способ определения динамического коэффициента внешнего трения скольжения при наклоне двух образцов, нижний из которых, имеющий форму диска, приводят во вращение вокруг своей оси и наклоняют относительно горизонта, удерживая верхний образец в том месте диска, где его линейная скорость направлена вверх по уклону, при этом динамический коэффициент трения определяют по текущему значению угла наклона φ в тот момент, когда верхний образец начинает соскальзывать вниз [патент РФ №2458336, кл. G01N 19/02, опубл. 10.08.2012]. Особенностью рассматриваемого способа, выбранного в качестве прототипа, является его сходство со способом определения статического коэффициента внешнего трения, для нахождения которого требуется лишь отключение вращения нижнего образца. Недостатком способа является необходимость проведения раздельных опытов для определения статического и динамического коэффициентов трения, а также необходимость устройства для вращения нижнего образца при определении динамического коэффициента внешнего трения.

Техническим результатом предлагаемого способа является возможность определения динамического и статического коэффициентов внешнего трения образцов в одном опыте, без измерения сил трения, на основании их взаимосвязи с геометрическими параметрами процесса и равенства работы, совершаемой образцом, соскальзывающим по криволинейной поверхности, уменьшению потенциальной энергии образца вследствие изменения его вертикального положения при соскальзывании.

Технический результат достигается тем, что для определения статического и динамического коэффициентов внешнего трения используют два расположенных друг на друге образца, один из которых, базовый образец, выполняют с вогнутой рабочей поверхностью сферической или цилиндрической формы, имеющей горизонтальную ось, и обеспечивают возможность его поворота относительно этой оси. Опорную поверхность второго, подвижного образца, выполняют плоской или выпуклой, с радиусом, не меньше радиуса рабочей поверхности базового образца. Подвижный образец помещают в нижнюю часть рабочей поверхности базового образца. Поворачивая базовый образец относительно горизонтальной оси, измеряют угол φ, образуемый линией, соединяющей центр опорной поверхности подвижного образца с осью рабочей поверхности базового образца, и вертикалью, проходящей через эту ось. С увеличением угла φ возрастает скатывающая сила, действующая на подвижный образец, удерживаемый силой трения. При достижении некоторого значения угла поворота φ₁ под действием скатывающей силы происходит соскальзывание подвижного образца в конечное положение, характеризуемое углом φ₂. По значению угла φ₁ определяют статический коэффициент трения как m_ст=tgφ₁. Используя значения углов φ₁ и φ₂, определяют динамический коэффициент внешнего трения по формуле m д и н = k ( cos ϕ 1 − cos ϕ 2 ) ( sin ϕ 2 − sin ϕ 1 ) , полученной из условия равенства работы, произведенной силой трения при соскальзывании образца, уменьшению потенциальной энергии подвижного образца вследствие изменения его положения по вертикали. Поправочный коэффициент k в формуле компенсирует несовпадение центра тяжести подвижного образца с рабочей поверхностью базового образца.

Для изменения давления между образцами, в общем случае влияющего на величину коэффициентов трения, на подвижный образец устанавливают приставку с уравновешивающим грузом, перемещением которого относительно приставки обеспечивают совмещение центра тяжести системы, включающей подвижный образец, приставку и уравновешивающий груз, с рабочей поверхностью базового образца.

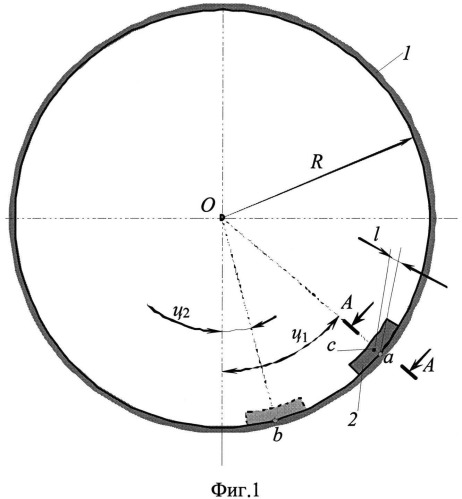
На фиг.1 показана схема реализации предлагаемого способа экспериментального определения статического и динамического коэффициентов внешнего трения;

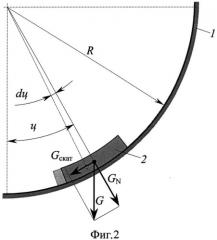
на фиг.2 показана схема действующих на образец сил;

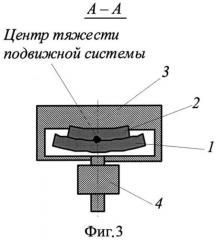
на фиг.3 показана в сечении А-А, перпендикулярном к направлению перемещения подвижного образца, схема реализации способа с использованием приставки и уравновешивающего груза, где

1 - базовый образец;

2 - подвижный образец;

3 - приставка;

4 - уравновешивающий груз.

Для определения статического и динамического коэффициентов внешнего трения используют базовый образец 1, выполненный с вогнутой рабочей поверхностью сферической или цилиндрической формы, и подвижный образец 2. Опорной поверхности подвижного образца 2 также придают соответственно сферическую или цилиндрическую, но выпуклую форму, ее радиус принимают не менее радиуса рабочей поверхности базового образца 1, чтобы исключить даже кратковременное движение подвижного образца 2 по принципу трения качения. Как частный случай, опорная поверхность подвижного образца 2 может быть исполнена плоской, радиус которой в таком случае может рассматриваться как бесконечно большой.

Ось рабочей поверхности базового образца 1 располагают горизонтально и обеспечивают возможность поворота относительно нее базового образца 1.

При проведении опыта подвижный образец 2 помещают в нижнюю часть рабочей поверхности базового образца 1, где на него не воздействует скатывающая сила. Для определения коэффициентов трения базовый образец 1 вместе с подвижным образцом 2 поворачивают относительно горизонтальной оси О (фиг.1), измеряя меняющийся угол φ между линией, проходящей через центр опорной поверхности подвижного образца и ось поворота рабочей поверхности О (фиг.1), и вертикалью, проходящей через ось поворота О рабочей поверхности.

Смещение подвижного образца 2 на угол φ соответствует размещению подвижного образца 2 на уклоне с таким же углом, с учетом того, что габариты подвижного образца 2 многократно меньше размеров базового образца 1, уклон на всей опорной поверхности подвижного образца 2 можно считать приближенно одинаковым, погрешность определения коэффициента трения вследствие этого практически несущественна.

Сила тяжести G находящегося на уклоне с углом φ подвижного образца 2 раскладывается на две составляющие (фиг.2): нормальную к поверхности G_N=G·cosφ и скатывающую G_ск=G·sinφ. Между подвижным образцом 2 и базовым образцом 1 в равновесном состоянии системы возникают соответствующие реакции: нормальная N=G_N и сила трения F_тр=G_скат. Пока равновесие сохраняется, подвижный образец 2 остается в состоянии покоя относительно базового образца 1. В некоторый момент подвижный образец 2 достигнет такого положения с углом φ₁, при котором сила трения станет предельной F_тр=G_N·m_стат, при этом условие равновесия примет вид

G·cosφ₁·m_стат=G·sinφ₁,

где m_стат - статический коэффициент трения.

В этот момент произойдет соскальзывание подвижного образца 2 вниз по уклону. Измеренный в момент соскальзывания угол φ₁ представляет собой угол статического трения, по величине которого определяют статический коэффициента трения m_ст=tgφ₁.

Величину динамического коэффициента внешнего трения m_дин определяют в зависимости от пути, пройденного подвижным образцом 2 после соскальзывания из положения с углом φ₁ в положение с углом φ₂, при котором соскальзывание завершится. Полная работа, которую совершает сила трения при изменении угловой координаты подвижного образца 2 от φ₁ до φ₂, определяется интегрированием элементарной работы, совершаемой изменяющейся силойы трения при соскальзывании подвижного образца 2 вдоль дуги ab (фиг.1). Элементарная работа, совершаемая силой трения при текущем значении угла φ и смещении подвижного образца 2 на некоторый бесконечно малый угол dφ (фиг.2), пропорциональна силе трения F_тр=G·cosφ·m_дин и пройденному подвижным образцом 2 пути dS=Rdφ, где R - радиус рабочей поверхности базового образца 1:

dA=G·cosφ·f_динRdφ.

Полная работа силы трения на пути ab определяется интегрированием

.

Уменьшение потенциальной энергии подвижного образца 2 при изменении его угловой координаты от φ₁ до φ₂ определяется как

W=G(R-1)(cosφ₁-cosφ₂),

где l - расстояние центра тяжести с подвижного образца 2 (фиг.1) от рабочей поверхности базового образца 1, зависящее от формы подвижного образца 2; при малых габаритах и пластинчатой форме подвижного образца l с достаточной точностью можно считать равным половине его толщины.

Из условия равенства работы силы трения изменению потенциальной энергии получим

G·m_дин·R(sinφ₂-sinφ₁)=G·(R-c)(cosφ₁-cosφ₂),

откуда следует

m д и н = k ( cos ϕ 1 − cos ϕ 2 ) ( sin ϕ 2 − sin ϕ 1 ) ,

где k - поправочный коэффициент, компенсирующий расстояние центра тяжести подвижного образца 2 от его опорной поверхности,

k = ( R − l ) R .

Для исследования коэффициентов трения при повышенных контактных давления на подвижный образец 2 устанавливают выполненную со сквозным отверстием приставку 3 с уравновешивающим грузом 4 (фиг.3), отсутствующие в общем случае и не показанные на фиг.1 и фиг.2. Для этого ширину базового образца 1 принимают меньше соответствующего размера отверстия в приставке 2. Уравновешивающий груз 4 устанавливают на приставке 3 с возможностью перемещения в радиальном направлении и обеспечивают такое его положение, при котором центр тяжести системы, включающей подвижный образец 2, приставку 3 и уравновешивающий груз 4, совпадает с рабочей поверхностью базового образца 1. В этом случае в выражении для определения динамического коэффициента внешнего трения принимают k=1.

Таким образом, предлагаемый способ является универсальным и позволяет определять в одном опыте статический и динамический коэффициенты внешнего трения, с переменным давлением между образцами.

1. Способ определения статического и динамического коэффициентов внешнего трения между двумя расположенными друг на друге базовом и подвижном образцами, отличающийся тем, что базовый образец выполняют с вогнутой рабочей поверхностью сферической или цилиндрической формы, ось которой располагают горизонтально, и обеспечивают возможность поворота базового образца относительно этой оси, подвижный образец выполняют с плоской или выпуклой опорной поверхностью, радиусом не менее радиуса рабочей поверхности базового образца, затем помещают подвижный образец в нижнюю часть рабочей поверхности базового образца; поворачивают базовый образец вокруг оси, измеряя угол между линией, соединяющей центр опорной поверхности подвижного образца с осью поворота рабочей поверхности, и вертикалью, проходящей через эту ось, по значениям угла φ₁, при котором происходит соскальзывание подвижного образца под действием силы тяжести, определяют статический коэффициент внешнего трения m_ст=tgφ₁, а с учетом значения угла φ₂, при котором соскальзывание подвижного образца прекращается, определяют динамический коэффициент внешнего трения по формуле m д и н = k ( cos ϕ 1 − cos ϕ 2 ) ( sin ϕ 2 − sin ϕ 1 ) , где k = ( R − l ) R , R - радиус рабочей поверхности базового образца, l - расстояние между центром тяжести подвижного образца и рабочей поверхностью базового образца.

2. Способ по п.1, отличающийся тем, что на подвижный образец устанавливают приставку со сквозным отверстием, помещают подвижный образец с приставкой на базовый образец, ширину которого выполняют менее ширины отверстия в приставке, на приставку устанавливают уравновешивающий груз, перемещением которого совмещают центр тяжести системы, включающей подвижный образец, приставку и уравновешивающий груз, с рабочей поверхностью базового образца, а значение k для определения динамического коэффициента внешнего трения принимают равным единице.