2538296 - Способ определения состояния кубита

Способ определения состояния кубита

Иллюстрации

Показать все

Изобретение относится к компьютерным системам, в частности к квантовым компьютерам и оптическим логическим элементам, и может быть использовано для полного определения состояния кубита. Техническим результатом является повышение точности измерений, сокращение времени измерения. Способ, основанный на считывании кубита в нескольких различных измерительных базисах, включающий воздействие на кубит электромагнитным излучением на переходах между уровнями кубита и некоторым вспомогательным уровнем. Для считывания кубита в требуемом измерительном базисе на кубит воздействуют бихроматическим излучением, спектральные компоненты которого резонансны переходам с уровней кубита на вспомогательный уровень, интенсивности и фазы спектральных компонент бихроматического излучения задают так, чтобы выделить требуемый для считывания кубита измерительный базис. Результат считывания определяют, регистрируя возбуждение кубита на вспомогательный уровень. 3 з.п. ф-лы, 5 ил.

Реферат

Изобретение относится к компьютерным системам, основанным на специфических вычислительных моделях, в частности к квантовым компьютерам и оптическим логическим элементам, и может быть использовано для полного определения состояния кубита.

В качестве базовых элементов квантового компьютера в настоящее время предлагается использовать кубиты - квантовые системы с двумя базисными состояниями |0> и |1>. В отличие от обычного цифрового компьютера, в котором минимальная единица информации - бит может принимать только два значения, «0» и «1», кубит может находиться как в состояниях |0> и |1>, так и в произвольном суперпозиционном состоянии:

| ψ 〉 = α | 0 〉 + β | 1 〉 , ( 1 )

где α и β - комплексные числа, связанные условием:

| α | 2 + | β | 2 = 1 ( 2 )

(см., например, М.Нильсен, И.Чанг «Квантовые вычисления и квантовая информация». М.: Мир, 2009, 33-37).

Выражение (1) называется разложением состояния |ψ〉 по базису состояний |0> и |1>, а числа α и β - проекциями состояния |ψ〉 на состояния |0> и |1> соответственно. В качестве базиса можно выбрать отличную от |0> и |1> пару состояний |0′> и |1′> (каждая из которых представляет суперпозицию состояний |0> и |1>) и аналогично (1) разложить состояние по базису состояний |0′> и |1′>:

| ψ 〉 = α ' | 0 ' 〉 + β ' | 1 ' 〉 , ( 3 )

где α′ и β′ - комплексные числа, связанные, как и α и β, условием:

| α ' | 2 + | β ' | 2 = 1 . ( 4 )

Для реализации квантовых вычислений необходимо обеспечить: инициализацию начального состояния кубита (загрузку данных), унитарные преобразования над кубитами (реализацию алгоритма вычислений) и считывание конечного состояния кубита (считывание результатов вычислений) (см., например, М.Нильсен, И.Чанг «Квантовые вычисления и квантовая информация». М.: Мир, 2009, 347-349).

Считывание кубита представляет собой квантовое измерение. Широко распространенным классом квантовых измерений являются проективные измерения. В этом случае квантовое измерение описывается набором определенных ортонормированных состояний (в случае кубита - набором из двух ортонормированных состояний), называемым измерительным базисом. Если представить состояние кубита |ψ〉 в виде разложения по измерительному базису |m> и |n>:

| ψ 〉 = c m | m 〉 + c n | n 〉 , ( 5 )

Для описания состояния квантовых систем широко используется матрица плотности ρ ^ (см., например, К.Блум «Теория матрицы плотности и ее приложения». М.: Мир, 1983), которая для кубита (квантовой системы с двумя базисными состояниями) представляет собой квадратную эрмитову матрицу 2×2.

ρ ^ = ( ρ 00 ρ 01 ρ 10 ρ 11 ) , ( 6 )

где ρ₀₀ и ρ₁₁ - действительные числа, удовлетворяющие условию:

ρ 00 + ρ 11 = 1 , ( 7 )

а ρ₀₁ и ρ₁₀ - комплексные числа, удовлетворяющие условию:

ρ 01 = ρ 10 * . ( 8 )

Элементы матрицы плотности зависят от выбора базиса. Пусть матрица плотности

записана в базисе состояний |0> и |1>. В этом случае диагональные элементы матрицы плотности ρ₀₀ и ρ₁₁ называются населенностями состояний |0> и |1> соответственно, а недиагональные элементы ρ₀₁ и ρ₁₀ - квантовыми когерентностями на переходе между состояниями |0> и |1>. С учетом условий (7) и (8) задание одного диагонального элемента матрицы плотности, то есть населенности, и одного недиагонального элемента матрицы плотности - квантовой когерентности позволяют полностью определить состояние кубита. Населенности ρ₀₀ и ρ₁₁ определяют вероятность обнаружить кубит в состояниях |0> и |1> соответственно, то есть при квантовом измерении состояния кубита, описываемого матрицей плотности ρ в измерительном базисе |0> и |1>, кубит с вероятностью ρ₀₀ будет обнаружен в состоянии |0>, а с вероятностью ρ₁₁ - в состоянии |1>.

Процедура квантового измерения в общем случае изменяет состояние измеряемой квантовой системы, поэтому проведение повторных измерений над одной и той же квантовой системой в общем случае не приводит к корректным результатам. Однако многократное проведение процедуры измерения над идентичными квантовыми системами (то есть системами, находящимися в одном и том же состоянии) позволяет определить населенности измерительного базиса.

В качестве кубитов предлагается использовать как одиночные квантовые системы, так и ансамбли таких систем, находящихся в одинаковом состоянии. В первом случае процедура считывания кубита в некотором измерительном базисе приводит к обнаружению кубита в одном из состояний измерительного базиса с вероятностями, определяемыми населенностями измерительного базиса. Многократное проведение процедуры считывания над идентичными кубитами позволяет измерить населенности измерительного базиса. Во втором случае считывание кубита в некотором измерительном базисе представляет собой одновременное квантовое измерение над большим количеством квантовых систем, находящихся в одинаковом состоянии, и позволяет непосредственно измерить населенности измерительного базиса.

Считывание кубита в любом заданном измерительном базисе, даже если оно проводится многократно, позволяет измерить только населенности измерительного базиса. Этого недостаточно для полного определения состояния кубита. Для полного определения состояния кубита необходимо также измерение квантовой когерентности на переходе между состояниями измерительного базиса. Однако оказывается, что при проведении измерений в нескольких различных измерительных базисах (в данном случае предполагается, что измерения проводятся над идентичными кубитами), можно полностью определить состояние кубита (см., например, М.Нильсен, И.Чанг «Квантовые вычисления и квантовая информация». М.: Мир, 2009, 483-484).

В настоящее время ведутся активные поиски квантовых систем, способных исполнять роль кубитов. Одним из перспективных подходов к физической реализации кубитов является использование активных центров (атомов, ионов и пр.) с долгоживущими энергетическими уровнями, с которых возможны переходы под действием электромагнитного излучения на некоторый вспомогательный энергетический уровень (или несколько энергетических уровней). При этом два из долгоживущих энергетических уровней используются для реализации кубита, а переходы на вспомогательный энергетический уровень (или несколько энергетических уровней) - для совершения унитарных преобразований над кубитом, инициализации начального состояния и считывания конечного состояния кубита. Перспективным является также использование в качестве кубитов ансамблей таких активных центров, в частности ансамблей ионов редкоземельных элементов в кристаллах.

Для считывания кубита можно непосредственно использовать электромагнитное излучение, резонансное переходу между энергетическими уровнями кубита. Однако такие переходы часто оказываются запрещены. Кроме того, пространственное разрешение такого измерения обычно ограничено длиной волны перехода между энергетическими уровнями кубита. Это обстоятельство, в случае кубитов с близкими энергиями уровней, ограничивает возможность селективного считывания кубитов.

Более удобным для считывания кубита оказывается использование электромагнитного излучения, резонансного переходу с одного из энергетических уровней кубита |0> или |1> на вспомогательный энергетический уровень. Для проведения операции считывания кубита на кубит воздействуют монохроматическим электромагнитным излучением, резонансным переходу с одного из энергетических уровней кубита, например |0>, на вспомогательный энергетический уровень. Таким образом, регистрируя возбуждение кубита (или отсутствие возбуждения) на вспомогательный энергетический уровень, производят считывание кубита. Для регистрации возбуждения измеряют поглощение резонансного электромагнитного излучения или населенность вспомогательного энергетического уровня, например, по сигналу флуоресценции с него. В случае кубитов на основе одиночных активных центров, если произошло возбуждение кубита на вспомогательный энергетический уровень, то результат считывания соответствует обнаружению кубита в состоянии |0>, если возбуждение кубита на вспомогательный энергетический уровень не произошло, то результат считывания соответствует обнаружению кубита в состоянии |1>. В случае кубитов на основе ансамблей активных центров населенность верхнего энергетического уровня в результате возбуждения и, соответственно, поглощение резонансного электромагнитного излучения и сигнал флюоресценции со вспомогательного энергетического уровня пропорциональны населенности состояния |0> считываемого кубита. Описанный способ считывания кубита предлагается использовать для считывания состояний кубита в методе обработки квантовой информации, известном из патента США (US 6800837 «Method for quantum information processing and quantum information processor)), МПК7 G02F 3/00, публ. 05.10.2004).

Известны также способы считывания кубита с помощью адиабатического переноса одного из энергетических уровней кубита на некоторый вспомогательный уровень с последующей регистрацией населенности вспомогательного уровня различными способами (см., например, патент США №US 7667853 «Quantum bit reading device and method », current CPC class G06N 99/002, публ. 23.02.2010 и патент США №US 7791052 «Single-photon generation apparatus and quantum bit reading apparatus and method», current CPC class G06N 99/002, публ. 07.09.2010).

Недостатком всех этих способов является то, что они позволяют провести считывание кубита только в одном измерительном базисе - базисе энергетических уровней кубита. Этого недостаточно для полного определения состояния кубита. Для полного определения состояния кубита необходима возможность считывания состояния кубита в нескольких различных измерительных базисах.

Наиболее близким аналогом по технической сущности к предлагаемому способу является способ определения состояния кубита, основанный на считывании кубита в нескольких различных измерительных базисах, который выбран в качестве прототипа (см. L.Rippe, В Julsgaard, A.Walther, Yan Ying, and S.Kroll, «Experimental quantum-state tomography of a solid-state qubit», Physical Review A, V.77, 022307 (2008)). Способ прототип позволяет проводить считывание кубита в произвольном требуемом измерительном базисе и на основе результатов считывания в нескольких измерительных базисах провести полное определение состояния кубита.

Считывание кубита в произвольном, наперед заданном измерительном базисе в способе-прототипе происходит в две стадии. На первой стадии производят преобразование кубита, переводящее заданный измерительный базис в базис энергетических уровней. Стадия включает в себя следующие шаги. На первом шаге на кубит воздействуют первым π-импульсом электромагнитного излучения. Первый π-импульс производит перенос населенности выбранного суперпозиционного состояния кубита на вспомогательный уровень |е>. На втором шаге на кубит воздействуют вторым π-импульсом, сдвинутым по фазе относительно первого. Второй π-импульс производит обратный перенос населенности вспомогательного уровня |е> в выбранное суперпозиционное состояние кубита. В результате выбранное суперпозиционное состояние приобретает набег фазы, определяемый сдвигом фаз между первым и вторым π-импульсами. Такая процедура позволяет перевести произвольный, наперед заданный измерительный базис в базис энергетических уровней. На второй стадии производят считывание кубита в базисе энергетических уровней. Для этого на кубит воздействуют монохроматическим излучением, резонансным переходу между одним из уровней кубита и вспомогательным уровнем. При этом измеряют поглощение резонансного монохроматического излучения. Результат считывания кубита определяют по поглощению резонансного монохроматического излучения.

Для кубитов на основе ансамблей активных центров по результату считывания кубита вычисляют населенность состояний измерительного базиса. В случае, если процедура измерения не откалибрована, то есть не известен коэффициент связи между поглощением монохроматического резонансного излучения и населенностью взаимодействующего с ним уровня кубита, в способе-прототипе используют дополнительное измерение на стадии считывания кубита в базисе энергетических уровней. Сначала на кубит воздействуют монохроматическим излучением, резонансным переходу между одним из уровней кубита и вспомогательным уровнем. При этом измеряют поглощение резонансного монохроматического излучения. После этого на кубит воздействуют монохроматическим излучением, резонансным переходу между вторым уровнем кубита и вспомогательным уровнем. При этом измеряют поглощение резонансного монохроматического излучения. На основе результатов измерений проводят калибровку процедуры измерения и вычисляют населенность состояний измерительного базиса.

Для полного определения состояния кубита в способе-прототипе производят измерение населенностей измерительного базиса в нескольких различных измерительных базисах, на основе результатов измерения полностью определяют состояние кубита.

Недостатками способа-прототипа являются: во-первых, необходимость сложной процедуры преобразования кубита, требующей точного контроля параметров используемых π-импульсов и разности фаз между ними; во-вторых, время, необходимое для преобразования, ограничено длительностью используемых л-импульсов; в-третьих, для проведения процедуры преобразования необходимо, чтобы время жизни населенности вспомогательного уровня |е> и время жизни квантовой когерентности на переходах между уровнями кубита и вспомогательным уровнем было больше длительности преобразования.

Задачей, решаемой настоящим изобретением, является разработка способа определения состояния кубита, основанного на считывании кубита в нескольких различных измерительных базисах, позволяющего производить считывание кубита в требуемом измерительном базисе без проведения преобразования над кубитом.

Технический результат в разработанном способе определения состояния кубита, как и в способе-прототипе, основанном на считывании кубита в нескольких различных измерительных базисах, достигается за счет того, что на кубит воздействуют электромагнитным излучением на переходах между уровнями кубита и некоторым вспомогательным уровнем.

Новым в разработанном способе определения состояния кубита является то, что для считывания кубита в требуемом измерительном базисе на кубит воздействуют бихроматическим излучением, спектральные компоненты которого резонансны переходам с уровней кубита на вспомогательный уровень, интенсивности и фазы спектральных компонент бихроматического излучения задают так, чтобы выделить требуемый для считывания кубита измерительный базис, при этом регистрируют возбуждение кубита на вспомогательный уровень.

В первом частном случае реализации разработанного способа возбуждение кубита на вспомогательный уровень целесообразно регистрировать по поглощению бихроматического излучения.

Во втором частном случае возбуждение кубита на вспомогательный уровень целесообразно регистрировать по флуоресценции с него.

В третьем частном случае целесообразно в качестве кубита использовать кубит на основе ансамблей редкоземельных ионов, допированных в кристалл.

В случае кубитов на основе ансамблей активных центров или при многократном считывании состояний идентичных кубитов на основе одиночных активных центров, на основе результатов считывания вычисляют населенности состояний измерительного базиса.

На основе нескольких таких измерений в нескольких различных измерительных базисах полностью определяют состояние кубита.

Разработанный способ не требует преобразования кубита. Это упрощает техническую реализацию метода и повышает точность измерений, так как он свободен от ошибок, связанных с процедурой преобразования кубита. Разработанный способ позволяет сократить время измерения, так как он не требует времени на преобразования кубита. Время t, необходимое для считывания кубита в каждом из нескольких требуемых для определения состояния кубита измерительных базисов, ограничено лишь спектральной шириной компонент импульса бихроматического излучения, которая не должна быть больше частоты перехода между уровнями кубита. То есть время t должно быть меньше 1/ω, где ω - частота перехода между уровнями кубита. Для разработанного способа не важно время жизни вспомогательного уровня и время жизни квантовой когерентности на переходах между уровнями кубита и вспомогательным уровнем.

Разработанный способ поясняется следующими фигурами:

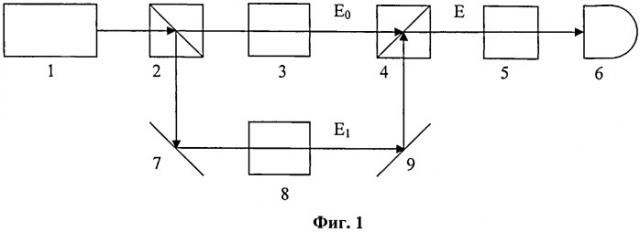
На фиг.1 представлена схема возможной технической реализации разработанного способа в соответствии с п.1 или п.2 формулы.

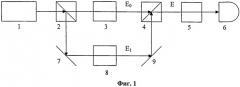
На фиг.2 представлена схема возможной технической реализации разработанного способа в соответствии с п.3 формулы.

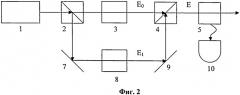
На фиг.3 представлен кубит, резонансно взаимодействующий с бихроматическим излучением E → = E 0 → e − i ω 0 t + E 1 → e − i ω 1 t через вспомогательный уровень, |0> и |1> - уровни кубита, |е> - вспомогательный уровень, используемый для реализации способа.

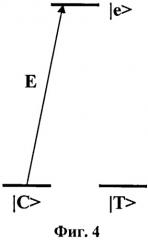
На фиг.4 представлен кубит в базисе светлого |C> и темного |Т> состояний, резонансно взаимодействующий с бихроматическим излучением E → = E 0 → e − i ω 0 t + E 1 → e − i ω 1 t через вспомогательный уровень.

На фиг.5 представлена схема рабочих уровней иона Pr³⁺ в кристалле LaF₃, используемых для реализации кубита на основе спектрально выделенных групп ионов Pr³⁺ в кристалле LaF₃ и для реализации разработанного способа определения состояния кубита.

Возможны различные технические реализации разработанного способа. Схема одной из возможных технических реализаций разработанного способа представлена на фиг.1. Она содержит лазер 1, делители пучка 2 и 4, акустооптические модуляторы 3 и 8, зеркала 7 и 9, кубит 5 и фотодетектор 6.

Способ определения состояния кубита в соответствии с п.1 формулы с помощью схемы, представленной на фиг.1, осуществляют следующим образом.

Частоту излучения лазера 1 выбирают близкой к частоте переходов с уровней кубита |0> и |1> на вспомогательный уровень |е>. Излучение лазера 1 разделяют на делителе пучка 2 на два пучка, каждый из пучков проходит через отдельный акустооптический модулятор 3 или 8. С помощью акустооптических модуляторов 3 и 8 смещают частоты излучения проходящих через них лазерных пучков так, чтобы они совпали с частотами переходов с уровней кубита |0> и |1> на вспомогательный уровень |е> соответственно и таким образом формируют компоненты резонансного бихроматического излучения Е₀ и E₁ (см. фиг.3). Компоненты резонансного бихроматического излучения Е₀ и E₁ совмещают на делителе пучка 4, и таким образом формируют резонансное бихроматическое излучение Е вида:

E → = E 0 → e − i ω 0 t + E 1 → e − i ω 1 t . ( 9 )

Резонансным бихроматическим излучением E воздействуют на кубит 5. Известно (см., например, Б.Д.Агапьев, М.Б.Горный, Б.Г.Матисов, Ю.В.Рождественский «Когерентное пленение населенности в квантовых системах» Успехи физических наук, Т. 163, №9, с.1-36 (1993)), что в этом случае резонансное бихроматическое излучение взаимодействует только с суперпозиционным состоянием уровней |0> и |1>, так называемым светлым состоянием |С>, а ортогональное светлому - также суперпозиционное, темное состояние |Т> не взаимодействует с бихроматическим полем (см. фиг.4). При этом светлое и темное состояния следующим образом зависят от компонент резонансного бихроматического излучения:

| T 〉 = Ω 1 Ω | 0 〉 − Ω 0 Ω | 1 〉 , ( 10 )

| C 〉 = Ω 1 * Ω | 0 〉 + Ω 0 − Ω | 1 〉 , ( 11 )

где Ω 0 = E 0 → , d → 0 / ℏ , Ω 1 = E 1 → , d → 1 / ℏ , - частоты Раби компонент бихроматического излучения, d → 0 , d → 1 - дипольные моменты переходов |0>→|е> и |1>→|е> соответственно Ω = | Ω 0 | 2 + | Ω 1 | 2 .

Авторами предлагается использовать этот эффект для считывания кубита в требуемом измерительном базисе и на основе считывания кубита в нескольких различных измерительных базисах полностью определять состояние кубита. С помощью акустооптических модуляторов 3 и 8 интенсивности и фазы спектральных компонент бихроматического излучения Е₀ и E₁ задают так, чтобы выделить требуемый для считывания кубита 5 измерительный базис, то есть так, чтобы описываемые выражениями (10) и (11) светлое |C> и темное состояния |Т> совпали с состояниями требуемого для считывания кубита измерительного базиса. При необходимости ограничить время измерения акустооптические модуляторы 3 и 8 также используют, чтобы сформировать импульс резонансного бихроматического излучения. При этом регистрируют возбуждение кубита 5 на вспомогательный уровень. Для чего, например, измеряют поглощение резонансного бихроматического излучения E при взаимодействии с кубитом 5 с помощью фотодетектора 6.

В случае кубитов на основе ансамблей активных центров населенность вспомогательного уровня в результате возбуждения пропорциональна населенности состояния |C> считываемого кубита 5.

В случае кубитов на основе одиночных активных центров, если произошло возбуждение кубита 5 на вспомогательный уровень, то результат считывания соответствует обнаружению кубита 5 в состоянии |C>. Если возбуждение кубита 5 на вспомогательный уровень не произошло, то результат считывания соответствует обнаружению кубита 5 в состоянии |T>.

В случае кубитов на основе ансамблей активных центров на основе результата считывания кубита вычисляют населенность состояний измерительного базиса. В случае кубитов на основе одиночных активных центров процедуру считывания проводят многократно над кубитами, находящимися в одинаковом состоянии, на основе результатов считывания кубитов вычисляют населенность состояний измерительного базиса.

Описанным выше образом проводят измерения населенностей измерительного базиса для нескольких (не меньше трех) различных измерительных базисов. Для этого проводят несколько (не меньше трех) различных измерений, в каждом из которых выбором интенсивностей и фаз спектральных компонент бихроматического излучения задают различные измерительные базисы. В каждом из измерений измеряют населенность состояния измерительного базиса |C>, описываемого выражением (11). Элементы матрицы плотности зависят от выбора базиса. Населенность состояния |C>, описываемого выражением (11), следующим образом связана с элементами матрицы плотности в базисе энергетических уровней кубита |0> и |1>

ρ с с = 1 Ω 2 ( | Ω 0 | 2 ρ 00 + ρ 11 + 2 Re ( Ω 0 Ω 1 * ρ 01 ) ) . ( 12 )

В результате нескольких измерений получают несколько различных значений населенности состояния |C>, соответствующих различным состояниям |С>. На основе результатов измерений полностью определяют состояние кубита.

В качестве примера можно предложить следующие три измерения. В первом измерении с помощью акуостооптических модуляторов 3 и 8 интенсивности и фазы спектральных компонент бихроматического излучения задают так, чтобы соответствующие им частоты Раби удовлетворяли следующему условию:

Ω 1 = 0 , Ω 0 − н е к о т о р а я п р о и з в о л ь н а я в е л и ч и н а , ( 13 )

при этом измеряют населенности измерительного базиса. В этом случае измеренная населенность состояния измерительного базиса |C> согласно выражению (12) запишется как:

ρ с с , 1 = ρ 00 . ( 14 )

Во втором измерении с помощью акустооптических модуляторов 3 и 8 интенсивности и фазы спектральных компонент бихроматического излучения задают так, чтобы соответствующие им частоты Раби удовлетворяли следующему условию:

Ω 0 = Ω 1 , ( 15 )

при этом измеряют населенности измерительного базиса. В этом случае измеренная населенность состояния измерительного базиса |C> согласно выражению (12) и условию (7) запишется как

ρ c c , 2 = l/2 + Re( ρ 01 ) .

Способ определения состояния кубита

Патент 2538296