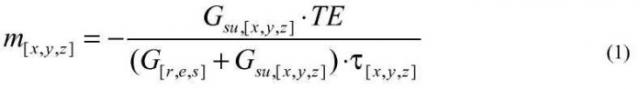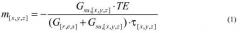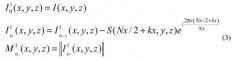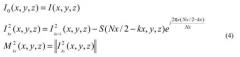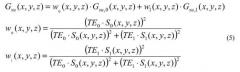Картирование градиента восприимчивости

Картирование градиента восприимчивости

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ИЗОБРЕТЕНИЯ

Настоящее изобретение относится к способу определения карты градиента восприимчивости, компьютерному программному продукту и устройству для определения карты градиента восприимчивости объекта посредством магнитно-резонансной визуализации.

В настоящее время широко используют формирующие изображение MR (магнитно-резонансные) способы, в которых используют взаимодействие между магнитными полями и ядерными спинами для того, чтобы формировать двухмерные или трехмерные изображения, особенно в области медицинской диагностики, поскольку для визуализации мягких тканей они превосходят другие способы визуализации во многих отношениях, для них не нужно ионизирующее излучение, и обычно они не инвазивны.

ПРЕДПОСЫЛКИ ИЗОБРЕТЕНИЯ

Согласно MR способу в целом, организм пациента или в целом объект нужно разместить в сильном, однородном магнитном поле, направление которого одновременно определяет ось (обычно ось z) системы координат, на которой основаны измерения. Магнитное поле создает различные энергетические уровни для отдельных ядерных спинов независимо от напряженности магнитного поля, эти ядерные спины можно возбуждать (спиновый резонанс) посредством наложения электромагнитного переменного поля (РЧ поле) определенной частоты (так называемая ларморова частота или MR частота). С микроскопической точки зрения распределение отдельных ядерных спинов создает общую намагниченность, которую можно отклонять от состояния равновесия посредством применения электромагнитного импульса подходящей частоты (РЧ импульса), причем магнитное поле идет перпендикулярно оси z, также обозначаемой как продольная ось, с тем чтобы намагниченность выполняла прецессионное движение вокруг оси z. Прецессионное движение описывает поверхность конуса, у которого угол апертуры обозначают как угол отклонения вектора намагниченности. Величина угла отклонения вектора намагниченности зависит от напряженности и длительности приложенного электромагнитного импульса. В случае так называемого перпендикулярного импульса спины отклоняются от оси z к поперечной плоскости (угол отклонения вектора намагниченности 90 градусов).

После завершения РЧ импульса намагниченность релаксирует в исходное состояние равновесия, в котором снова создается намагниченность в направлении оси z при первой постоянной времени T1 (время спинрешеточной или продольной релаксации), а намагниченность в направлении, перпендикулярном направлению оси z, релаксирует при второй постоянной времени T2 (спиновое или поперечное время релаксации). Изменение намагниченности можно обнаруживать посредством приемных РЧ катушек, которые размещают и ориентируют в пределах исследуемого объема MR устройства таким образом, чтобы измерять изменение намагниченности в направлении, перпендикулярном оси z. Затухание поперечной намагниченности после применения, например, перпендикулярного импульса сопровождается переходом ядерных спинов, индуцированным локальными неоднородностями магнитного пола, из упорядоченного состояния с такой же фазой в состояние, в котором все фазовые углы распределены равномерно (дефазирование). Дефазирование можно компенсировать посредством повторной фокусировки импульса, например, противоположно направленному импульсу. Это создает эхо-сигнал (спиновое эхо) в приемных катушках.

Для того чтобы реализовать пространственное разрешение в организме, линейные градиенты магнитного поля, идущие вдоль трех основных осей, накладывают на равномерное магнитное поле, что ведет к линейной пространственной зависимости резонансной частоты спина. Тогда сигнал, принятый приемными катушками, содержит компоненты с различными частотами, которые можно ассоциировать с различными местоположениями в организме. Данные сигналов, полученные через приемные катушки, соответствуют пространственному частотному домену и их называют данными k-пространства. Данные k-пространства обычно содержат множество линий, полученных с различным фазовым кодированием. Каждую линию оцифровывают посредством сбора нескольких образцов. Массив данных k-пространства преобразуют в MR изображение с помощью преобразования Фурье.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Объект, обладающий магнитной восприимчивостью, которая отличается от окружения, создает локальные неоднородности основного магнитного поля. Это относится к металлическим объектам, таким как хирургические инструменты, имплантаты или другие устройства, железосодержащие материалы, такие как кровь, деоксигенированная кровь и встречающиеся в природе отложения железа в тканях, или контрастные средства на основе оксида железа или меченые клетки. Это также относится к пустотам в пределах визуализируемого организма, поскольку существует значительная разность в восприимчивости между пустотами (заполненными газом) и окружающими тканями. Использование этого эффекта является важным инструментом для различных применений MR визуализации от обнаружения контрастного средства (например, SPIO) и встречающихся в природе границ тканей до локализации устройств, таких как катетеры и имплантаты.

Контрастную MR визуализацию восприимчивости обычно осуществляют через T2 или T2* взвешенные последовательности. С помощью этих последовательностей контраст создают с помощью потерь сигналов на стороне локального возмущения магнитного поля. В изображениях, генерируемых с помощью этих известных способов, темные признаки изображения, которые обусловлены неоднородностями поля, нельзя отличить от признаков, которые обусловлены другими эффектами, ведущими к потерям сигналов, таким как низкая плотность спинов или очень короткое время T2.

Предложено несколько MR последовательностей для преобразования этого темного сигнала в положительный контраст. Различные подходы показывают изображения с ярким положительным контрастом, но необходимы первоначальные знания о напряженности возмущения поля для того, чтобы оптимизировать положительный контраст изображения. Этого избегают с помощью нескольких способов последующей обработки, которые разработаны для вычисления положительного контраста из градиентного эхо-изображения. Во время получения градиентных эхо-изображений, градиенты восприимчивости локально изменяют накладываемые градиенты визуализации. В дополнение к общеизвестному геометрическому искажению, это ведет к сдвигу затронутого эха в k-пространстве. Определение этого сдвига для каждого вокселя визуализации (трехмерного пикселя) ведет к карте градиентов, индуцированных восприимчивостью.

Для того чтобы определить карту градиента восприимчивости, в настоящее время используют два алгоритма. Первый алгоритм представляет собой алгоритм «оригинального картирования градиента восприимчивости» (SGM), который основан на вычислении преобразований Фурье малых членов. Этот способ идентичен рассмотренному, например, в WO 2007/122527 A2. Второй способ, который дает карты градиента восприимчивости при более высоком разрешении, основан на использовании усеченных преобразований Фурье. Этот алгоритм, в дальнейшем обозначаемый как «SGM с истинным разрешением», подробно описан в Dahnke H, Liu W, Bowtell R, Frank JA, High Resolution Positive Contrast via Post-processing from Conventional 3D Imaging, Int Soc Magn Reson Med 2008; 16 1513. Он основан на способе анализа энергетического спектра k-пространства, представленном в Chen N, Oshio K, Panych LP, Application of k-space energy spectrum analysis to susceptibility field mapping and distortion correction in gradient-echo EPI, Neurolmage 2006; 31:609-622.

Алгоритмы для SGM с истинным разрешением связаны с очень высоким временем вычисления, что препятствует их применению в клинической практике. Время вычисления для двухмерной карты для изображения 64×64×1 с использованием алгоритма, предложенного в цитированной выше работе авторов посредством Chen et al., типично составляет приблизительно 11 секунд, что подразумевает, например, что для типичного клинического массива данных для головного мозга (256×256×150) время вычисления составит порядка 40 часов. Усовершенствования SGM с истинным разрешением, как предложено в цитированной выше работе авторов Dahnke et al., могут снизить время вычисления порядка 20 часов, что, тем не менее, все еще слишком долго для клинического применения.

Следовательно, легко понять, что существует необходимость в усовершенствованном способе для определения карты градиента восприимчивости с истинным разрешением с высоким качеством и высокой скоростью. Следовательно, цель изобретения также состоит в том, чтобы предоставить MR устройство, которое делает возможным определение карты градиента восприимчивости с истинным разрешением с высоким качеством и высокой скоростью.

Согласно изобретению, раскрыт способ определения карты градиента восприимчивости. Способ включает получение массива магнитно-резонансных данных о k-пространстве, указанный массив данных содержит данные о магнитно-резонансном эхе и преобразование полученного массива данных о k-пространстве в массив данных изображения I(x, y, z), где для заданного направления k-пространства, например x, способ включает следующие стадии:

a) осуществление одномерного дискретного преобразования Фурье массива данных изображения вдоль заданного направления k-пространства; указанное одномерное преобразование Фурье ведет к набору членов Фурье, каждый член Фурье из указанного набора связан с указателем k-пространства вдоль заданного направления k-пространства (x),

b) выбор значения усечения (kx), непрерывно меняющегося между -N/2 и N/2 вдоль указанного направления k-пространства, где N представляет собой размер массива данных о k-пространстве вдоль этого направления,

c) рекурсивная генерация обновленного массива данных изображения I_kx ¹(x, y, z) посредством определения члена Фурье из набора членов Фурье, у которого числовой указатель k-пространства соответствует указанному значению усечения, и вычитание определяемого члена Фурье из массива данных изображения I_kx-1 ¹(x, y, z), сгенерированного на непосредственно предшествующей стадии генерации массива данных изображения; указанное вычитание ведет к новому обновленному массиву данных изображения I_kx ¹(x, y, z),

d) вычисление величины M_kx ¹(x, y, z) нового обновленного массива данных изображения,

e) повторение стадий с b) до d) с увеличением или уменьшением значения усечения (kx),

f) вычисление эхо-сдвига (m) для заданного направления k-пространства по изменениям величин между новыми обновленными массивами данных изображения,

g) вычисление градиента восприимчивости (G_su) вдоль заданного направления k-пространства по указанному эхо-сдвигу.

Предпочтительно указанные выше стадии осуществляют для всех направлений k-пространства, где после этого различные карты градиентов восприимчивости можно комбинировать в одну карту градиента величины.

Способ в соответствии с изобретением позволяет значительно сократить время вычисления по сравнению с известными способами SGM с истинным разрешением известного уровня техники для определения карты градиента восприимчивости без снижения качества, что делает возможным применение этого способа в клинической практике. Например, в случае использования клинических массивов данных, описанных выше, в качестве соответствующих массивов данных о k-пространстве можно получить время вычисления порядка 10 минут.

Таким образом, в соответствии с настоящим изобретением, применение повторных полноразмерных трехмерных преобразований Фурье, как известно из способов SGM с истинным разрешением известного уровня техники, заменяют на последовательный алгоритм, в котором рекурсивное отношение используют для обновления вычисления усеченных преобразований Фурье на каждой итерации. Получаемый алгоритм вычисляет трехмерный SGM приблизительно за N_x×N_y×N_z×(N_x+N_y+N_z) операций, таким образом делая возможной обработку больших трехмерных массивов данных, которые встречаются, например, в неврологическом применении, за разумное время.

В целом, входные данные способа SGM предпочтительно представляют собой трехмерное, а также, возможно, двухмерное комплексное изображение, полученное с использованием эхо-последовательности, например, градиентной эхо-последовательности. Известно, что градиентные эхо-последовательности чувствительны к неоднородности B0 в целом и к локальным изменениям магнитной восприимчивости, в частности. Известно несколько эффектов или артефактов, обусловленных неоднородностью B0, индуцированной восприимчивостью, таких как геометрическое искажение, внезапное ослабление сигнала и эхо-сдвиги. В способе SGM локальные эхо-сдвиги, возникающие в результате градиентов неоднородности B0, используют для получения карты этих градиентов.

Локальный эхо-сдвиг m, обусловленный градиентом неоднородности B0, индуцированной восприимчивостью, G_su задают следующим уравнением:

где G представляет собой градиент визуализации, наложенный на одно из трех направлений в пространстве (r: считывание, e: фазовое кодирование, s: срез), τ представляет собой временной интервал, во время которого накладывают градиент G (время задержки для направления считывания), и ТЕ представляет собой желаемое эхо-время последовательности.

Для этого уравнения ясно, что эхо-сдвиг увеличивает линейность при эхо-времени ТЕ для заданного градиента G_su.

Отношение в приведенном выше уравнении можно обратить, чтобы получить упрощенную формулу, которая связывает эхо-сдвиг в k-пространстве и напряженность градиента восприимчивости G_su:

где G_su представляет собой градиент неоднородности B0, индуцированной восприимчивостью, G представляет собой градиент визуализации (или приращение градиента), наложенный на одно из трех направлений в пространстве (r: считывание, e: фазовое кодирование, s: срез), m представляет собой эхо-сдвиг, τ представляет собой временной интервал, во время которого накладывают градиент G (время задержки для направления считывания), и ТЕ представляет собой желаемое эхо-время последовательности.

Способ SGM с истинным разрешением продолжается вычислением локально (т.е. для каждого вокселя) количества эхо-сдвига в каждом направлении в пространстве. Эту стадию выполняют посредством спектрального анализа k-пространства. Принцип этого анализа проиллюстрирован далее в случае вычисления эхо-сдвига в направлении оси x. С учетом того, что S(kx, ky, kz) обозначает полученный сигнал k-пространства, а N_x обозначает размер матрицы дискретизации в направлении оси x, алгоритм SGM с истинным разрешением осуществляет следующие стадии:

- для каждого значения kx=-Nx/2... 0 задать все образцы S(k, ky, kz), k<kx, равными 0. Это усеченное количество далее обозначают как Skx¹. Затем вычисляют величину трехмерного преобразования Фурье для Skx¹, обозначенную Mkx.

Вычислить для каждого вокселя сумму: M₁(x, y, z)=Σ_kx M_kx ¹ (х, y, z).

Повторить аналогичную процедуру для kx=+Nx/2... 0, которая дает М₂(х, y, z).

Вычислить эхо-сдвиг как нормализованную разность: (M₂(x, y, z)-M₁(x, y, z))/M(x, y, z), где M представляет собой величину трехмерного преобразования Фурье для S (без какого-либо усечения).

Изменение количества M_kx как функции степени усечения kx изображено на фиг.1 в отсутствие градиента неоднородности B0 и на фиг.2 в присутствии градиента неоднородности B0. Падение сигнала 100 наблюдают для kx=0 в первом случае и падение сигнала 200 для kx≠0 во втором случае. Тогда разность М₂(х, y, z)-M₁(x, y, z) пропорциональна эхо-сдвигу m_x (см. номер позиции 202 на фиг.2) в направлении оси x, что дает возможность вычисления градиента восприимчивости G_sux с помощью приведенного выше уравнения (2).

Как можно понять из приведенного выше описания, касающегося SGM с истинным разрешением известного уровня техники, повторные полноразмерные трехмерные преобразования Фурье всех усеченных полученных сигналов k-пространства осуществляют в способе SGM с истинным разрешением, который, таким образом, требует много времени.

В соответствии с настоящим изобретением, усечение полученного сигнала k-пространства и последующее трехмерное преобразование Фурье заменяют последовательным алгоритмом, в котором используют рекурсивное отношение. Это можно понять с помощью следующих уравнений:

Здесь I(x, y, z) обозначает трехмерное комплексное изображение, I_kx ¹(x, y, z) - трехмерное преобразование Фурье усеченного сигнала S_kx ¹ (k, ky, kz), и S(k, y, z) - k-й коэффициент Фурье одномерного преобразования Фурье (вдоль направления оси x) изображения I(x, y, z), где k=0 соответствует «нулевой» частотный член. Следует отметить, что трехмерное комплексное изображение I(x, y, z) можно получить посредством трехмерного преобразования Фурье сигнала S(kx, ky, kz).

Приведенное выше уравнение предоставляет способ эффективного вычисления членов M_kx ¹(x, y, z), участвующих в вычислении M₁. Для вычисления M₂ обозначим соответствующее отношение:

Следует отметить, что описанный выше способ осуществляют предпочтительно для всех вокселей (x, y, z). Предпочтительно вычитание между I_kn ¹ и членом Фурье выполняют повоксельно. Кроме того, следует отметить, что вычисление и хранение экспонент в уравнении (3) и (4) осуществляют только один раз для каждого значения усечения, например посредством оценки и хранения в явной форме соответствующих косинусоидальных и синусоидальных членов. Затем эти экспоненты можно повторно использовать при итерациях по всем вокселям. Эти экспоненты зависят только от значения усечения и, например, в случае направления оси x, на «x», а не по другим двум осям «y» и «z».

Этот алгоритм вычисляет трехмерный SGM приблизительно за (Nx+Ny+Nz)×Nx×Ny×Nz операций. Для сравнения исходный алгоритм (с использованием повторных трехмерных преобразований Фурье) требует (Nx+Ny+Nz)×(Nx×Ny×Nz)×ln(Nx×Ny×Nz) операций для аналогичного вычисления, и использование только одномерных преобразований Фурье, без применения рекурсивных отношений, требует Nx×Ny×Nz×(Nx×ln(Nx)+Ny×ln(Ny)+Ny×ln(Ny)) операций.

В приведенном выше описании вычисляют M₁ и M₂ и затем используют для того, чтобы вычислить эхо-сдвиг с помощью нормализованной разности между M₂ и M₁. Это соответствует варианту осуществления изобретения, где в первом цикле на стадии b значение усечения непрерывно увеличивается от 0 до половины размера массива данных о k-пространстве вдоль указанного направления k-пространства, что ведет к стадии с в первых новых обновленных массивах данных изображения и на стадии d к первым величинам. Кроме того, в этом варианте осуществления во втором цикле на стадии b значение усечения непрерывно снижается от 0 до минус половины размера массива данных о k-пространстве вдоль указанного направления k-пространства, что ведет на стадии с ко вторым новым обновленным массивам данных изображения и на стадии d ко вторым величинам. Кроме того, на стадии f эхо-сдвиг вычисляют по разности между суммой всех вторых величин всех вторых новых обновленных массивов данных изображения и суммой всех первых величин всех первых новых обновленных массивов данных изображения.

Однако следует отметить, что это является лишь вариантом осуществления. Как правило, достаточно сравнить на стадии f изменения величин для различных значений усечения k-пространства и определить указатель k-пространства, при котором изменение интенсивности возникает для каждого вокселя. Посредством определения указателя k-пространства, при котором возникает изменение интенсивности, можно определить сдвиг в k-пространстве для каждого вокселя.

Признак использования значения усечения между 0 и половиной размера массива данных о k-пространстве вдоль заданного направления k-пространства в сочетании с вычислением эхо-сдвига по разности между суммой всех величин первых и вторых обновленных массивов данных изображений (т.е. M₂-M₁) предназначен для надежного определения эхо-сдвига. Следовательно, усечение k-пространства осуществляют с этой целью отдельно для обеих половин k-пространства, от +k_max до k₀ (k₀=0) и в другом направлении от -k_max до k₀. Однако любой другой способ определения указателя k-пространства, при котором возникает изменение интенсивности, можно использовать для каждого вокселя в комбинации, для которой последовательный и рекурсивный алгоритм рассмотрены на стадии с.

В соответствии с дополнительным вариантом осуществления изобретения, после каждой отдельной стадии вычисления первой или второй величины указанную фактически вычисленную первую или вторую величину прибавляют к уже вычисленной сумме всех первых и вторых величин, что ведет к новой (т.е. до настоящего момента), уже вычисленной сумме всех первых или вторых величин. Т.е. после каждого обновления M_kx ¹ и M_kx ² осуществляют вычисление сумм M₁ и M₂. Это ограничивает требования предложенного алгоритма к запоминающему устройству. Вместо хранения отдельных величин после стадии вычисления каждой величины в памяти вновь вычисленную величину просто прибавляют к предварительно определенной величине, математически выраженной как M_new=M_new+M_{actually calculated}.

В соответствии с дополнительным вариантом осуществления изобретения, способ дополнительно включает повторение стадий с a до g для всех остальных направлений k-пространства. Например, эти направления k-пространства содержат одно из направления градиента считывания, направления фазового кодирования или направления кодирования среза. Следовательно, посредством повторения всех стадий можно предоставить общую карту градиента.

В соответствии с дополнительным вариантом осуществления изобретения, трехмерные и одномерные дискретные преобразования Фурье представляют собой быстрые преобразования Фурье (БПФ). Следовательно, дополнительно увеличивается скорость алгоритма.

В соответствии с дополнительным вариантом осуществления изобретения, в том случае, когда стадию с (т.е. стадию рекурсивного алгоритма) осуществляют в первый раз, способ включает генерацию начального массива данных изображения посредством трехмерного преобразования Фурье полученного массива данных о k-пространстве, где в этом случае на стадии с предыдущую стадию генерации массива данных изображения задает генерация указанного начального массива данных изображения. Другими словами, изначально осуществляют трехмерное преобразование Фурье полученного массива данных о k-пространстве, что ведет к начальному массиву данных изображения, который используют в качестве начальной точки для рекурсивной генерации обновленных массивов данных изображения на стадии с. Следовательно, генерации самого первого («обновленного») изображения определяемого члена Фурье вычитают из начального массива данных изображения, результатом чего является обновленный массив данных изображения, который можно использовать для последующих рекурсивных стадий.

В соответствии с дополнительным вариантом осуществления изобретения, полученный массив данных содержит данные о магнитно-резонансном эхе для множества эхо с различными эхо-временами, где карту градиента восприимчивости определяют отдельно для каждого эхо-времени, что ведет к временной карте градиента восприимчивости, где способ дополнительно содержит вычисление общей карты градиента восприимчивости посредством комбинации всех определяемых временных карт градиентов восприимчивости. Например, множество эхо представляет собой двойное эхо. Это позволяет дополнительно повысить качество получаемых карт градиентов восприимчивости без какой-либо заметной задержки в регистрации и времени обработки данных.

Для того чтобы понять это глубже со ссылкой на уравнение (2), применение этого уравнения дает измерение градиента восприимчивости, которое не зависит от конкретного выбора эхо-времени ТЕ. Однако выбор ТЕ оказывает влияние на SNR (отношение сигнала к шуму) вычисленной карты градиента восприимчивости. Полагая, что градиентное эхо-изображение, используемое для вычисления G_su, характеризуется с помощью SNR, равного S/σ (S и σ представляют собой локальную амплитуду сигнала и стандартное отклонение шума соответственно), можно показать, что стандартное отклонение шума в вычислении эхо-сдвига m пропорционально σ/S. Из уравнения (2) в итоге можно вывести, что стандартное отклонение шума карты градиента восприимчивости пропорционально σ/(S×TE) для заданных параметров регистрации G и τ.

Таким образом, увеличение эхо-времени оказывает прямое влияние на SNR для SGM: удвоение эхо-времени удваивает SNR карты градиента восприимчивости. Однако на амплитуду сигнала S также влияет ТЕ через поперечные времена релаксации T2*. Несмотря на то, что снижение шума, достигнутое посредством увеличения ТЕ, обычно превосходит потери сигнала вследствие экспоненциального затухания T2*, можно наблюдать очень быстрое затухание сигнала, если градиент неоднородности B0 очень велик. В этой ситуации может локально отсутствовать доступный сигнал при приложенном ТЕ для вычисления градиента восприимчивости.

Для того чтобы получить пользу от высокого SNR, обусловленного длинными эхо-временами, во время избегания полной потери сигнала вследствие очень большой неоднородности B0, в соответствии с одним из вариантов осуществления используют подход двойного эха (или в целом подход мультиэхо). Градиентное эхо-изображение при коротком времени эхо-времени TE₀ получают в дополнение к градиентному эхо-изображению, полученному при «обычном» эхо-времени TE₁. Как правило, поскольку TE₁ достаточно велико, это можно осуществить в двойном эхо-сканировании без каких-либо издержек во времени сканирования. Один из примеров, иллюстрирующих выбор TE₀ и TE₁, заключается в том, что TE₁ по меньшей мере в 3 раза превышает TE₀.

По двум градиентным эхо-изображениям S₀ и S₁ можно вычислить две карты градиентов восприимчивости G_su,0 и G_su,1 посредством применения рассмотренного выше способа SGM. Однако в целом любой способ SGM можно использовать в сочетании с этим мультиэхом (например, двойным эхом) способом. Комбинируя две карты G_SU,0 и G_su,1, получают оптимальную карту градиента восприимчивости G_su.

Несмотря на то, что существует множество различных путей для комбинации этих двух карт, в соответствии с одним из вариантов осуществления изобретения можно использовать линейную комбинацию с весами w₀ и w₁, которые выбирают с тем, чтобы минимизировать шум в финальных картах. Это дает следующее уравнение:

Веса w₀ и w₁ зависят от локальных амплитуд сигнала S₀(x, y, z) и S₁(x, y, z). В уравнении (5) сделано допущение, что стандартные отклонения шума S₀ и S₁ идентичны, что имеет место, если два изображения получены с одинаковыми параметрами последовательности, за исключением эхо-времени, как в подходе двойного эха. В ином случае определение w₀ и w₁ следует модифицировать соответствующим образом.

С уравнением (5) для весов w₀ и w₁ достигают оптимального автоматического баланса для каждого пикселя между силой сигнала и эхо-временем. Получаемая карта градиента восприимчивости G_su имеет усовершенствованное SNR по сравнению с каждой из двух карт G_su,0 и G_su,1 и поддается меньшему влиянию со стороны потерь сигналов, чем G_su,1. Степень, в которой можно полностью избежать артефактов, обусловленных очень быстро затухающим сигналом, зависит от минимально достижимого эхо-времени TE₀ (обычно порядка 2-3 мс), пространственного разрешения градиентных эхо-изображений и напряженности неоднородности B0.

Для того чтобы преодолеть эти ограничения, в соответствии с одним из вариантов осуществления изобретения, регистрацию первого эха можно осуществить с использованием ультракороткой эхо-временной последовательности, такой как UTE (описано, например, в Rahmer J, Boernert P, Groen J, Bos С 3D Radial ultrashort echo-time imaging with T2 adapted sampling. Magn Reson Med 2006;55:1075-1082).

Возможно расширение предложенного способа на регистрацию множества эхо-изображений. С этой целью можно применять множественную эхоградиентную эхо-последовательность, как используют для T2* картирования. Альтернативно изображения можно получать раздельно с увеличенными эхо-временами, что допускает более высокую гибкость в выборе эхо-времени. Затем вычисляют карты градиентов восприимчивости G_su,i для каждого эхо-времени TE₁. Комбинацию отдельных карт G_su,i, чтобы получить оптимальную карту G_su, выполняют посредством обобщения уравнения (5) согласно:

Подход мультиэха имеет преимущество, состоящее в том, что конкретный выбор эхо-времени почти не оказывает влияния на получаемое SGM. В идеале пользователь может только решать, сколько времени потратить на сканирование, а выбор числа эхо-времен и интервалов между ними происходит автоматически с помощью системы. Эта установка гарантирует максимальную воспроизводимость результатов SGM для одного пользователя и между пользователями.

В другом аспекте изобретение относится к способу определения карты градиента восприимчивости, способ включает получение массива магнитно-резонансных данных о k-пространстве, указанный массив данных содержит данные о магнитно-резонансном эхе, где полученный массив данных содержит данные о магнитно-резонансном эхе для множества эхо с различными эхо-временами, где карту градиента восприимчивости определяют отдельно для каждого эхо-времени, что ведет к временной карте градиента восприимчивости, где способ дополнительно содержит вычисление общей карты градиента восприимчивости посредством комбинации всех определяемых временных карт градиентов восприимчивости, т.е. этот способ можно использовать вместе со способом SGM любого типа.

В другом аспекте изобретение относится к компьютерному программному продукту, содержащему исполняемые компьютером инструкции для осуществления способов, как описано выше.

В другом аспекте изобретение относится к устройству для определения карты градиента восприимчивости объекта посредством магнитно-резонансной визуализации, где устройство содержит систему регистрации данных для получения массива магнитно-резонансных данных о k-пространстве, указанный массив данных содержит магнитно-резонансные данные, где устройство выполнено с возможностью преобразования полученного массива данных о k-пространстве в массив данных изображения I(x, y, z), где для заданного направления k-пространства, например x, устройство дополнительно выполнено с возможностью:

a) осуществления одномерного дискретного преобразования Фурье массива данных изображения вдоль заданного направления k-пространства; указанное одномерное преобразование Фурье ведет к набору членов Фурье, каждый член Фурье из указанного набора ассоциирован с указателем k-пространства вдоль заданного направления k-пространства,

b) выбора значения усечения (kx), непрерывно меняющегося между -N/2 и N/2 вдоль указанного направления k-пространства, где N представляет собой размер массива данных о k-пространстве в этом направлении,

c) рекурсивной генерации (формулы 3 и 4) массива данных изображения I_kx ¹(x, y, z) посредством определения члена Фурье из набора членов Фурье, которым ассоциирован указатель k-пространства, соответствующий указанному значению усечения, и вычитания определяемого члена Фурье из массива данных изображения I_kx-1 ¹(x, y, z), сгенерированного на непосредственной предыдущей стадии генерации массива данных изображения; указанное вычитание ведет к новому обновленному массиву данных изображения I_kx ¹(x, y, z),

d) вычисления величины M_kx нового обновленного массива данных изображения,

e) повторения стадий с b) до d) с увеличением или уменьшением значения усечения (kx),

f) вычисления для заданного направления k-пространства эхо-сдвига (m) по изменениям величин между новыми обновленными массивами данных изображения,

g) вычисления градиента восприимчивости (G_su) вдоль заданного направления k-пространства по указанному эхо-сдвигу.

Предпочтительно указанные выше стадии осуществляются для всех направлений k-пространства, где после этого различные карты градиентов восприимчивости можно комбинировать в одну карту градиента величины.

В другом аспекте изобретение относится к устройству для определения карты градиента восприимчивости объекта посредством магнитно-резонансной визуализации, где устройство содержит систему регистрации данных для получения массива магнитно-резонансных данных о k-пространстве, содержащего данные о магнитно-резонансном эхе для множества эхо с различными эхо-временами, где устройство выполнено с возможностью

a) определения карты градиента восприимчивости отдельно для каждого эхо-времени, что ведет к временной карте градиента восприимчивости,

b) вычисления общей карты градиента восприимчивости посредством комбинации всех определяемых временных карт градиентов восприимчивости.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Включенные чертежи раскрывают предпочтительные варианты осуществления настоящего изобретения. Однако следует понимать, что чертежи созданы только с целью иллюстрирования, но не в качестве определения пределов изобретения. На чертежах:

на фиг.1 проиллюстрировано развитие амплитуды усеченного сигнала как функции степени усечения в отсутствие градиента неоднородности B0;

на фиг.2 проиллюстрировано развитие амплитуды усеченного сигнала как функции степени усечения в присутствии градиента неоднородности B0;

на фиг.3 представлена блок-схема, иллюстрирующая различные стадии способа в соответствии с изобретением;

на фиг.4 проиллюстрированы различные изображения, полученные для двойного эхо-картирования градиента восприимчивости при 3T;

на фиг.5 представлен MR сканер в соответствии с изобретением.

ПОДРОБНОЕ ОПИСАНИЕ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ

На фиг.1 и 2 проиллюстрировано развитие амплитуды усеченного сигнала M_kx как функции степени усечения kx в отсутствие (фиг.1) и в присутствии (фиг.2) градиента неоднородности B0. На фиг.1 падение сигнала 100 наблюдают для kx=0, тогда как на фиг.2 падение сигнала 200 наблюдают для значения kx≠0. Это ведет к эхо-сдвигу 202, который делает возможным вычисление градиента восприимчивости G_su,x с помощью уравнения 2, как указано выше в подробностях. В целом, вычитание площади под обеими кривыми интенсивности, представленными на фиг.1 и 2, и нормализация интенсивности вокселя ведет к сдвигу эха для каждого вокселя. Осуществление этой процедуры для всех направлений в пространстве и предпочтительно для всех вокселей делает возможным генерацию карты градиента восприимчивости.

На фиг.3 представлена блок-схема, иллюстрирующая отдельные стадии способа определения карты градиента восприимчивости. Способ начинается на стадии 300 с регистрации массива магнитно-резонансных данных о k-пространстве, где этот массив данных содержит данные о магнитно-резонансном эхе. На стадии 302 массив данных трансформируют в трехмерное изображение (I), что представляет собой следующую стадию 304, на которой задают желаемое направление k-пространства.

После этого на стадии 306 осуществляют одномерное дискретное преобразование Фурье, например посредством быстрого преобразования Фурье, на массиве данных изображения вдоль направления k-пространства, заданного на стадии 304. Это ведет к набору членов Фурье, где каждый член Фурье из указанного набора ассоциирован с соответствующим указателем k-пространства вдоль заданного направления k-пространства. В формулах 3 и 4 эти члены соответствуют коэффициентам Фурье S(k,y,z), умноженным на соответствующую экспоненту.

Способ продолжается стадией 308, на которой kn и h задают равными 1. Здесь n указывает направление в пространстве, заданное на стадии 304, т.е. n представляет собой, например, направление x, у или z в данном вариа