Способ определения характеристики колебательного движения элемента турбомашины

Способ определения характеристики колебательного движения элемента турбомашины

Иллюстрации

Показать все

Реферат

Изобретение относится к области турбомашиностроения и может быть использовано при проектировании и поузловой доводке элементов ступеней турбомашин, а именно рабочих колес, колес направляющих и сопловых аппаратов.

Известен способ определения параметров колебаний лопаток турбомашин (RU 2484439, опубл. 10.06.2013), заключающийся в бесконтактном измерении и непрерывном контроле амплитуды и частоты колебаний турбинных и компрессорных лопаток в эксплуатационных условиях. Измерение параметров колебаний осуществляется за счет установки радиолокационного устройства на базовом расстоянии от турбомашины под острым углом к перпендикуляру плоскости вращения лопаток, выделения частот Доплера сигнала, отраженного от движущихся лопаток турбомашины, выделения частоты Доплера сигнала от каждой движущейся лопатки, получения автокорреляционных функций сигналов, полученных для каждой i-й лопатки, определения амплитуды колебаний каждой i-й лопатки на основе сравнения значений автокорреляционных функций с порогом, по результатам сравнения судят об амплитуде колебаний, дополнительно определяют текущие значения скорости вращения лопаток турбомашины.

Недостатком известного способа является сложность осуществления процесса измерений и необходимость сложной математической обработки результатов измерений. Кроме того, использование данного способа измерений не позволяет получить связь частоты колебаний с конструктивными параметрами турбомашины.

Известен способ возбуждения и определения параметров колебаний лопаток турбомашин (RU 2240526, опубл. 20.11.2004), заключающийся в измерении параметров колебаний лопаток посредством их тензометрирования. Способ обеспечивает проведение испытаний на разных частотах вращения при разных нагрузках и позволяет определить несколько форм колебаний лопаток рабочего колеса турбомашины.

Использование известного способа также не позволяет установить однозначную зависимость частоты и формы колебаний от конструктивных параметров исследуемой ступени турбомашины.

Задачей изобретения является создание способа, обеспечивающего выявление форм и частот колебаний элементов турбомашины в составе ее ступени и установление зависимости частоты и формы колебаний от конструктивных параметров исследуемой ступени турбомашины.

Технический результат заключается в ускорении и упрощении процесса поузловой доводки элементов ступеней турбомашин, а именно рабочих колес, колес направляющих и сопловых аппаратов, посредством установления зависимости частоты и формы колебаний от конструктивных параметров исследуемой ступени турбомашины. В смысле заявленного изобретения доводка осуществляется путем изменения количества лопаток.

Поставленная задача решается тем, что реализуют способ определения характеристики колебательного движения элемента турбомашины, содержащей установленную в корпусе по меньшей мере одну ступень с рабочим колесом и направляющим или сопловым аппаратом. Способ характеризуется тем, что подсчитывают количество лопаток рабочего колеса, подсчитывают количество лопаток направляющего или соплового аппарата, вычисляют предполагаемые резонансные частоты колебаний рабочего колеса в рабочем диапазоне частот вращения турбомашины, экспериментально выявляют резонансные частоты колебаний рабочего колеса, сопоставляют значения предполагаемых и экспериментально выявленных резонансных частот колебаний и по результату сопоставления определяют качественную составляющую и/или количественную составляющую характеристики колебательного движения элемента турбомашины.

При этом в качестве характеристики колебательного движения элемента турбомашины определяют номер формы диаметральных колебаний рабочего колеса. Также в качестве характеристики колебательного движения элемента турбомашины определяют частоту собственных колебаний лопаток рабочего колеса. Кроме того, в качестве характеристики колебательного движения элемента турбомашины определяют частоту вибраций корпуса турбомашины.

Указанные существенные признаки обеспечивают решение поставленной задачи, так как:

подсчет количества лопаток рабочего колеса, направляющего или соплового аппарата и вычисление резонансных частот колебаний рабочего колеса обеспечивает установление связи характеристики колебательного движения с конструктивными параметрами исследуемой ступени турбомашины;

экспериментальное выявление резонансных частот колебаний рабочего колеса также обеспечивает установление связи характеристики колебательного движения с конструктивными параметрами исследуемой ступени турбомашины;

сопоставление значений предполагаемых и экспериментально выявленных резонансных частот колебаний позволяет определить качественную составляющую и/или количественную составляющую характеристики колебательного движения элемента турбомашины, упростить тем самым установление зависимости частоты и формы колебаний от конструктивных параметров исследуемой ступени турбомашины и ускорить процесс доводки элементов ступеней турбомашин.

Изобретение поясняется чертежами, где

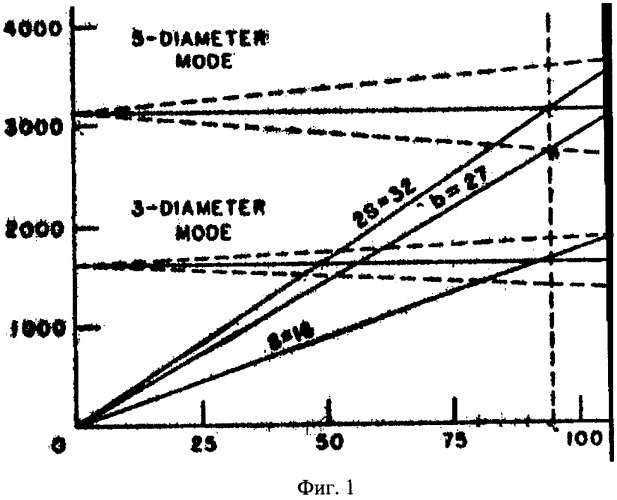
на фиг.1 показана диаграмма Кэмпбела для водяной турбины Френсиса;

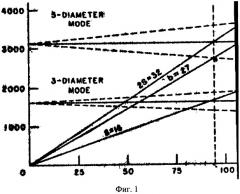
на фиг.2 - резонансная диаграмма (диаграмма Кэмпбела) для кольца гидроподшипника;

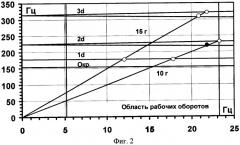
на фиг.3 - осциллограмма и спектрограмма тензосигнала лопатки колеса первой ступени компрессора низкого давления на режиме возникновения резонансных колебаний;

на фиг.4 - осциллограмма и спектрограмма пульсаций давления газа над лопаткой первой ступени компрессора низкого давления на режиме возникновения резонансных колебаний;

на фиг.5 - осциллограмма и спектрограмма тензосигнала лопатки колеса второй ступени компрессора низкого давления на режиме возникновения резонансных колебаний;

на фиг.6 - осциллограмма и спектрограмма пульсаций давления газа над лопаткой второй ступени компрессора низкого давления на режиме возникновения резонансных колебаний.

Способ реализуется следующим образом.

Для определения характеристики колебательного движения элемента турбомашины первоначально подсчитывают количество лопаток рабочего колеса (РК) и количество лопаток направляющего аппарата (НА) в случае исследования компрессора или количество лопаток соплового аппарата (СА) в случае исследования турбины. Далее вычисляют предполагаемые резонансные частоты колебаний рабочего колеса в рабочем диапазоне частот вращения турбомашины.

Для вычисления предполагаемых резонансных частот используют модифицированную формулу, выражающую условие возникновения резонанса, левая и правая часть которой умножена на частоту вращения:

N(S×m±n)=N(R×l),

где n, m, l - целые числа;

N - частота вращения;

S - число лопаток направляющего или соплового аппарата;

R - число лопаток рабочего колеса.

Экспериментальное определение резонансных частот колебаний осуществляют одним из стандартных способов, например с использованием способа, описанного в RU 2240526. Далее проводят сопоставление значений вычисленных и экспериментально выявленных резонансных частот колебаний.

Сопоставление значений вычисленных и экспериментально выявленных резонансных частот колебаний позволяет определить как качественные, так и количественные характеристики колебательного движения элемента турбомашины. В частности, можно определить форму колебательного движения РК: диаметральную или зонтичную. Можно определить номер формы диаметральных колебаний РК. Посредством сопоставления определяется частота собственных колебаний лопаток, а также частота вибраций корпуса турбомашины. Возможно определение и других характеристик.

Для пояснения существа заявленного способа разберем несколько примеров.

Один из подходов, используемых при проектировании и доводке элементов ступеней турбомашин, связан с изучением ротор-статорного взаимодействия.

Впервые с проблемой ротор-статорного взаимодействия столкнулся Дж. П. Ден Гартог в 1929 году, когда исследовал колебания трубопровода водяной турбины Френсиса [1], и этот пример был приведен в его книге «Механические колебания» [2].

На одной гидростанции были обнаружены очень сильные колебания труб, подводящих воду к водяным турбинам. Трубы издавали такое громкое жужжание, что оно было слышно за несколько километров. Кроме того, возникло опасение, что сильные колебания труб могут привести к разрушению здания, в котором располагались турбины. Чтобы избавится от колебаний трубопровода, рабочее колесо турбины, имевшее 17 лопаток, было извлечено из турбины и заменено колесом с 16 лопатками. После замены рабочего колеса амплитуда колебаний трубы была понижена до одной трети от своего первоначального значения.

Проанализируем данный пример, используя идею механического генератора, представляющего ступень турбомашины и состоящего из вращающегося рабочего колеса, направляющего аппарата и водяного потока.

Рабочее колесо (РК) турбины имело 17 лопаток, направляющий аппарат (НА) - 18. Если сопоставить число лопаток РК и НА, то можно получить равенство: 18-17=1, которое можно записать в виде:

18 − 1 = 17                                                                ( 1 )

Исходя из приведенного примера условие возникновения резонанса можно записать в форме для механического генератора, который состоит из РК, НА и потока по следующему алгоритму:

1. В левой части равенства должно стоять число, соответствующее количеству лопаток неподвижной части ступени. Это число лопаток НА или соплового аппарата (СА) - S.

2. К числу S прибавляется или вычитается n - число узловых диаметров (номер формы диаметральных колебаний).

3. В правой части равенства должно стоять число, соответствующее количеству лопаток рабочего колеса, - R.

4. Поскольку равенство типа (1) всегда должно выполняться для данного количества узловых диаметров n, то возможны комбинации S и R, когда множителями S и R будут целые числа m и l, выбранные таким образом, чтобы имело место условие возникновения резонанса

S×m±n=R×l.

5. Резонансные частоты можно получить, умножив обе части равенства на частоту вращения. При этом S, умноженное на частоту вращения, дает частоту колебаний вращающегося колеса, R, умноженное на частоту вращения, дает частоту колебаний неподвижной части генератора механических колебаний.

Применим описанный выше алгоритм к равенству (1): умножение обеих частей равенства на частоту вращения турбины 6,66 Гц дает в результате: 119,88-6,66=113,22 Гц - частоту колебаний трубопровода. Частота колебаний трубопровода в приведенном примере была равна 113,33 Гц. Следовательно, умножение числа лопаток РК на частоту вращения колеса, равную 6,66 Гц, позволяет получить частоту колебаний, равную 113,22 Гц, т.е. практически совпадающую с искомой частотой колебаний - 113,33 Гц.

Сопоставим теперь, как было сделано ранее, числа, отражающие количество лопаток РК и НА для измененного варианта турбомашины с РК, имевшим 16 лопаток:

1 8 − 2 = 1 6                                                ( 2 )

Сравнивая (1) и (2), обратим внимание на числа 1 и 2. Физически они означают, что в первом случае в рабочем колесе возбуждалась бегущая против вращения колеса волна с одним диаметром (номер формы диаметральных колебаний равен единице), в то время как во втором случае возбуждалась бегущая против вращения колеса волна с двумя диаметрами (вторая диаметральная форма колебаний). Поскольку энергия, запасаемая колесом для формы колебаний с двумя диаметрами, меньше, чем с одним диаметром, то амплитуда колебаний уменьшилась и это уже можно было рассматривать как достаточно удовлетворительное решение возникшей проблемы.

В дальнейшем с проблемой ротор-статорного взаимодействия столкнулся Ф. Кушнер [3], когда разбирал случаи усталостного разрушения по собственным формам колебаний рабочих колес центробежных компрессоров. Им были разработаны правила, согласно которым осуществлялась подборка коэффициентов отклика для различных конфигураций РК и НА. Хотя эти правила были довольно сложны для практического применения, он привел несколько примеров, когда сопоставление количества лопаток в РК и количества лопаток в НА позволило объяснить появление или отсутствие некоторых резонансов. Рассмотрим эти примеры исходя из приведенного выше алгоритма.

Рабочее колесо имело R=27 лопаток, количество статорных лопаток S было равно 16. Напишем равенство

1 6 × 2 − 5 = 2 7                                           ( 3 )

На диаграмме Кэмпбелла для РК с S=16, R=27 [4] (см. фиг.1) показаны рассматриваемые Ф. Кушнером два примера.

Умножим обе части равенства (3) на частоту вращения и получим:

32×98,43-5×98,43=27×98,43

где 32×98,43=3150 Гц - частота колебаний РК, взятая из рис.18 работы [5]. Как видно из равенства (3), эта частота соответствует форме с пятью узловыми диаметрами (номер формы диаметральных колебаний равен пяти). При этом узловые линии остаются неподвижными, то есть на вращающемся колесе реализуется стоячая волна.

Для формы колебаний с тремя узловыми диаметрами (номер формы диаметральных колебаний равен трем) условия возникновения резонанса можно записать в виде:

1 6 × 1 5 + 3 = 2 7 × 9                                  ( 4 )

Для n=95 Гц, f=1520 Гц (из работы [5], рис.19), умножив на 95 обе части равенства (4), получим:

(16×15)×95+3×95=(27×9)×95

27×9=243

243×95=23085

23085-285=22800

22800:15=1520 Гц

То есть возбуждаются колебания по форме с тремя узловыми диаметрами и на частоте вращения 95 Гц реализуется стоячая волна. В работе [5] Кушнер не рассматривал такую возможность и констатировал отсутствие резонанса по форме с тремя узловыми диаметрами.

Дальнейшее развитие эта тема получила в работе Тайлера и Софрина [3], которые создали теорию излучения шума от осевых турбомашин. Согласно этой теории вращающееся поле давления газа порождает в окружном направлении картину с числом диаметров k, определяемым из соотношения:

nS±k=mR,

где k - порядок (номер) диаметральной формы (число узловых диаметров), n - порядок возбуждающих гармоник во вращающейся системе координат, m - порядок возбуждающих гармоник в неподвижной системе координат.

Если в исследуемом рабочем колесе имеется форма колебаний с тем же самым числом диаметров и той же собственной частотой колебаний, которая имеет место в возбуждающем поле давления, то в рабочем колесе могут возникнуть резонансные колебания, и если не будет обеспечено достаточное демпфирование, то такой резонанс может привести к усталостному разрушению колеса.

Соотношение, полученное Софриным и Тайлером, было использовано в работе [6] при объяснении поломки кольца, приваренного к подшипнику водяного насоса охлаждения первого контура реактора на атомной станции Фукусима в январе 1988 г. Рабочий диапазон частот вращения насоса лежал в пределах от 20 до 100% при максимальной частоте вращения 1395 об/мин (23,25 Гц). Большую часть времени насос работал на частоте вращения 92% (21,39 Гц).

Теоретическим и экспериментальными путями были определены формы и частоты колебаний кольца, которые приводятся в таблице 1.

Таблица 1
Форма колебаний	0 диаметров	1 диаметр	2 диаметра	3 диаметра
Собственная частота колебаний в воде, Гц	154	178	217/231	306/323
Расчетная частота, Гц	160	176	222	317

Центробежное колесо компрессора имело 5 лопаток (R=5), диффузор имел 2 лопатки (S=2). При подстановке R и S в уравнение Софрина-Тайлера были получены различные комбинации вращающихся полей давления в неподвижной системе координат [6]:

Для m=1 (главная волна в неподвижной системе координат):

k=1 (n=2) и k=-1 (n=3)

k=3 (n=1) и k=-3 (n=4)

k=5 (n=0) и k=-5 (n=-5)

Для m=2 (вторая высшая гармоника):

k=0 (n=5)

k=2 (n=4) и k=-2 (n=6)

k=4 (n=3) и k=-4 (n=7) и т.д.

Для m=3 (третья высшая гармоника):

k=1 (n=7) и k=-1 (n=8)

k=3 (n=6) и k=-3 (n=9)

k=5 (n=5) и k=-5 (n=10) и т.д.

Как видно из вышеприведенного, нечетные гармоники порождают генерацию вращающегося поля давлений с нечетными номерами форм колебаний в стационарной системе, четные гармоники порождают четные номера диаметральных форм.

В источнике [6] на рис.9 представлена резонансная диаграмма, на которую нанесены собственные частоты кольца (для k=0, ±1, ±2 и ±3), возбуждающие частоты (главная, вторая и третья гармоники), обусловленные ротор-статорным взаимодействием, и частота вращения насоса в процентах. Поскольку нечетные (или четные) гармоники возбуждают колебания нечетных (или четных) номеров диаметральных форм (номеров узловых диаметров), при пересечении линиями гармоник горизонтальных линий собственных частот колебаний соответствующих диаметральных форм могут возникнуть резонансные колебания, обусловленные взаимодействием охлаждающей жидкости и кольца подшипника.

Поскольку диапазон рабочих оборотов РК насоса определен в пределах от 20% до 100% (рис.9 [6]), то можно приблизительно определить, на каких оборотах могут возникнуть колебания с 0, 1, 2 и 3 узловыми диаметрами, и построить по этим данным таблицу 2.

Таблица 2
%	Гц	f, Гц	Гармоника	Форма колебаний
51	11,86	178	15	1d
66,2	15,4	154	10	Окр
87,7	20,4	306	15	3d
92	21,39	213,9	10	2d
92,6	21,53	323	15	3d
100	23,25	232,5	10	2d

По приведенным в таблице 2 частотам и формам колебаний построена резонансная диаграмма для кольца гидроподшипника (диаграмма Кэмпбелла), где гармоники приведены к физической частоте вращения (числу оборотов) насоса (см. фиг.2).

Для экспериментального определения резонансных частот вблизи сварного соединения кольца к подшипнику были наклеены тензодатчики и проведено тензометрирование кольца в диапазоне рабочих оборотов насоса от 20 до 100%. Наблюдаемые пики деформаций соответствовали указанным диаметральным формам колебаний и совпадали с предсказанными на основе резонансной диаграммы. Резонанс, который привел к разрушению водяного насоса, соответствовал форме k=-2 (двухдиаметральной форме колебаний кольца, назад бегущая волна) и имел место на рабочих оборотах 92% - наиболее часто используемых при работе насоса.

Однако если рассматривать соотношение Софрина-Тайлера для m=2 и k=-2, то получается

2 × 6 − 2 = 5 × 2                                            ( 5 )

При умножении обеих частей равенства (5) на частоту вращения 21,53 Гц, соответствующую 92% от максимальной частоты вращения, получим:

(2×6)×21,53-2×21,53=215,3; (2×6)×21,53=258,36 Гц.

Из таблицы 1 видно, что форма колебаний кольца гидроподшипника с 2d (двумя диаметрами) возбуждается в полосе частот 217/231 Гц и частота 258,36 Гц выпадает из этого диапазона.

Аналогично распишем соотношение

2 × 4 + 2 = 5 × 2                                              ( 6 )

При умножении обеих частей равенства (6) на частоту вращения 21,53 Гц, соответствующую 92% от максимальной частоты вращения, получим:

(2×4)×21,53+2×21,53=215,3; (2×4)×21,53=172,24 Гц.

Частота 171,12 Гц близка к частоте 178 Гц, соответствующей форме колебаний кольца с одним диаметром, что опять находится в противоречии с выводом о причине разрушения кольца.

Рассмотренный пример является наглядным в том смысле, что в нем имеется почти полный набор данных для анализа причины разрушения за исключением экспериментальных данных, подтверждающих наличие форм и частот колебаний охлаждающей жидкости в центробежном насосе или хотя бы частот колебаний кольца, полученных при его тензометрировании. С этой позиции трудно проверить резонансную диаграмму, поскольку если привязываться к частотам вращения рабочего колеса, то колебания по форме два диаметра с назад бегущей волной не должны возбудиться.

Существует две точки зрения на проблему ротор-статорного взаимодействия. Первая - газодинамическая, когда предметом исследования являются газовые потоки, и вторая - прочностная, когда изучается отклик элементов ступени турбомашины на воздействие этих потоков.

В источнике [7] опубликован метод анализа потоков в многоступенчатых компрессорах, который был применен к трехступенчатому компрессору CREATE. Трехступенчатый высокоскоростной осевой компрессор сконструирован и построен французской фирмой Снекма и испытывался в Лаборатории Механики Жидкости и Акустики. Его геометрия и скорости вращения соответствуют современному гражданскому турбовентиляторному двигателю. На этапе конструирования этого компрессора количество лопаток на ступень выбиралось таким образом, чтобы уменьшить периферическую периодичность до 2π/16.

Количества лопаток в компрессорных венцах следующие:

Лопатки/венец	IGV	R1	S1	R2	S2	R3	S3
Для 2π	32	64	96	80	112	80	128
Для 2π/16	2	4	6	5	7	5	8

Применение правила (1) к ступеням этого компрессора показало:

для 1 ступени S1=96, R1=64

9 6 × 2 = 6 4 × 3                                                  ( 7 )

для 2 ступени S2=112, R2=80

1 1 2 × 5 = 8 0 × 7                                             ( 8 )

для 3 ступени S3=128, R3=80

1 2 8 × 5 = 8 0 × 8             ( 9 )

то есть в данной конструкции практически исключено появление низших диаметральных форм колебаний рабочих колес и венцов направляющих аппаратов.

Следует отметить, что на стадии проектирования выбор количества лопаток в венцах следует признать удачным с точки зрения прочности, поскольку оказалось, что в любой ступени компрессора практически невозможно создать ситуацию, при которой будут возбуждаться колебания колес с малым числом диаметров. Могут возникнуть только зонтичные формы колебаний, но поскольку энергии, забираемой от потока, в этих формах запасается меньше, чем в диаметральных, то и вероятность разрушения рабочих колес и венцов направляющих аппаратов меньше.

Применим описанный алгоритм к компрессору низкого давления (КНД) с входным направляющим аппаратом (ВНА).

Для первой ступени КНД с ВНА=23, R1=37 и S1=54 применение правила (1) дает следующий результат:

2 4 + 1 4 = 3 7                                                   ( 1 0 )

При тензометрировании лопаток первой ступени КНД на частоте вращения 140,707 Гц были обнаружены колебания с частотой 3236 Гц и напряжениями 3,24 кг/мм² (см. фиг.3).

Умножение равенства (10) на частоту вращения дает следующий результат:

23×140,707+14×140,707=37×140,707,

23×140,707=3236 Гц (см. фиг.3),

37×140,707=5206 Гц (см. фиг.4).

По датчику пульсаций, расположенному на корпусе компрессора, были обнаружены пульсации давления газа с частотой 5194 Гц (см. фиг.4).

Для колеса второй ступени КНД с R2=45 и S1=54 применение правила (1) дает следующий результат:

5 4 − 9 = 4 5                                                    ( 1 1 )

При тензометрировании лопаток второй ступени КНД на частоте вращения 122,77 Гц были обнаружены колебания с частотой 6635 Гц и напряжениями 6,99 кг/мм² (см. фиг.5).

Умножение равенства (11) на частоту вращения дает следующий результат:

54×122,77-9×122,77=45×122,77,

54×122,77=6629 Гц (см. фиг.5),

45×122,77=5524 Гц (см. фиг.6).

По датчику пульсаций, расположенному на корпусе компрессора, были обнаружены пульсации давления газа с частотой 5521 Гц (см. фиг.6).

Как следует из приведенных примеров, использование заявленного способа при проектировании и доводке элементов ступеней турбомашин обеспечивает выявление форм и частот колебаний элементов турбомашины в составе ее ступени и установление зависимости частоты и формы колебаний от конструктивных параметров исследуемой ступени и турбомашины в целом. Способ обеспечивает упрощение доводки элементов ступеней турбомашин, причем доводка осуществляется изменением количества лопаток РК, НА или СА.

Источники информации

1. Den Gartog, J.P., Mechanical vibrations in penstocks of hydraulic turbine installations, Transactions of ASME, 1929, p.102-110.

2. Дж. П. Ден Гартог. Механические колебания. Физматгиз, 1960.

3. J.M. Tyler, and T.G. Sofrin, Axial flow compressor noise studies, Transactions of the SAE, Vol. 70, pp.309-332.

4. F. Kushner, Disk vibration - rotating blade and stationary vane interaction. Transactions of the ASME, Journal of mechanical design, July 1980, Vol. 102, p.579-584.

5. F. Kushner, Rotating component modal analysis and resonance avoidance recommendations. Proceedings of the thirty-third turbomachinery symposium. 2004, p.143-161.

6. H. Ohashi, Case study of pump failure due to rotor-stator interaction. International journal of rotating machinery, 1994, Vol. 1, №1, pp.53-60.

7. N. Courtiade, X. Ottavy, and N. Gourdain, Modal decomposition for the analysis of the rotor-stator interactions in multistage compressors, Journal of thermal science, Vol. 21, №3 (2012), 276-285.

1. Способ определения характеристики колебательного движения элемента турбомашины, содержащей установленную в корпусе по меньшей мере одну ступень с рабочим колесом и направляющим или сопловым аппаратом, характеризующийся тем, что подсчитывают количество лопаток рабочего колеса, подсчитывают количество лопаток направляющего или соплового аппарата, вычисляют предполагаемые резонансные частоты колебаний рабочего колеса в рабочем диапазоне частот вращения турбомашины, экспериментально выявляют резонансные частоты колебаний рабочего колеса, сопоставляют значения предполагаемых и экспериментально выявленных резонансных частот колебаний и по результату сопоставления определяют качественную составляющую и/или количественную составляющую характеристики колебательного движения элемента турбомашины.

2. Способ по п.1, характеризующийся тем, что в качестве характеристики колебательного движения элемента турбомашины определяют номер формы диаметральных колебаний рабочего колеса.

3. Способ по п.1, характеризующийся тем, что в качестве характеристики колебательного движения элемента турбомашины определяют частоту собственных колебаний лопаток рабочего колеса.

4. Способ по п.1, характеризующийся тем, что в качестве характеристики колебательного движения элемента турбомашины определяют частоту вибраций корпуса турбомашины.