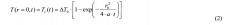Способ определения профиля теплопроводности горных пород в скважине

Способ определения профиля теплопроводности горных пород в скважине

Иллюстрации

Показать все

Реферат

Изобретение относится к геофизическим исследованиям скважин и может найти применение для определения тепловых свойств пластов горных пород, окружающих скважины.

Знание тепловых свойств и, в частности, теплопроводности горных пород необходимо для моделирования и оптимизации процесса добычи нефти и газа, особенно для оптимизации тепловых способов добычи тяжелых нефтей. Тепловые свойства пород обычно измеряют в лабораторных условиях на образцах керна, извлеченного из скважины. При этом результаты измерения теплоемкости пород вполне применимы для моделирования поля температур нефтяного пласта, а результаты измерения теплопроводности керна могут существенно отличаться от теплопроводности блоков горных пород in-situ. Это связано с:

(1) изменением свойств пород керна при бурении,

(2) отличием лабораторных РТ условий от пластовых,

(3) влиянием свойств пластовых флюидов, которое не всегда учитывают при проведении лабораторных измерений.

Одной из важнейших проблем является представительность результатов лабораторных измерений. Обычно выход керна существенно ниже 100% и лабораторные исследования не дают информации о свойствах трещиноватых пропластков и слабо консолидированных пород (где выход керна мал), что могут существенно повлиять на величину теплопроводности больших блоков горных пород, которая используется при моделировании резервуаров. Поэтому в дополнение к лабораторным исследованиям на керне на протяжении многих лет проводят эксперименты по определению тепловых свойств пород in-situ в скважине, но до настоящего времени не разработан пригодный для практического использования способ или прибор.

Было предложено много различных подходов к определению теплопроводности пород in-situ. Например, предлагалось использовать для этой цели процесс восстановления невозмущенной температуры массива после бурения или после промывки скважины (см. Дахнов В.Н., Дьяконов Д.И. Термические исследования скважин. Москва, ГНТИНГТЛ, 1952, 128 с.). Недостатком этого способа является сильная зависимость результатов измерений от перетоков и свободной тепловой конвекции флюида в скважине, от радиуса скважины и положения датчика температуры в скважине. Кроме того, сложно точно смоделировать тепловое возбуждение массива при бурении или промывке скважины, что необходимо для количественной интерпретации измеренной температуры и оценки тепловых свойств пород.

Большая часть работ по определению теплопроводности пород in-situ основана на теории линейного источника тепла. В скважину помещают достаточно длинный (3-5 м) нагреваемый зонд и регистрируют скорость увеличения температуры этого зонда, которая зависит от тепловых свойств окружающих пород (см., например, Huenges, E., Burhardt, H., and Erbas, K., 1990. Thermal conductivity profile of the KTB pilot corehole. Scientific Drilling, 1, 224-230). Основными недостатками этого способа являются большое время (порядка 12 часов), необходимое для измерения тепловых свойств на каждом участке скважины, искажения, связанные со свободной тепловой конвекцией флюида в скважине, и необходимость подвода к скважинному зонду значительной электрической мощности.

Некоторые способы используют небольшие нагреваемые зонды, которые прижимают к стенке скважины (см. Kiyohashi H., Okumura K., Sakaguchi K., and Matsuki K., 2000). Development of direct measurement method for thermophysical properties of reservoir rocks in situ by well logging. Proceedings World Geothermal Congress 2000, Kyushu-Tohoku, Japan, May 28 - June 10, 2000. Эти способы позволяют уменьшить продолжительность измерений, однако они требуют гладких стенок скважины, сложного оборудования, сложной численной модели для определения тепловых свойств пород по результатам измерения температуры зонда и позволяют оценить тепловые свойства только очень тонкого (1-3 см) слоя породы вблизи стенок скважины. Этот слой был подвергнут механическим напряжениям при бурении, может иметь техногенную трещиноватость, поры в породе заполнены буровым раствором, а не пластовым флюидом, поэтому тепловые свойства этого слоя могут существенно отличаться от свойств пород вдали от скважины.

Известны также способы, использующие подвижные зонды. Источник тепла находится в головной части зонда, датчик температуры - на конце зонда (см., например, патент США 3,892,128). Эти способы позволяют быстро оценивать тепловые свойства пород на значительном интервале глубин, однако, как и в предыдущем случае, они дают информацию о свойствах только очень тонкого слоя пород вокруг скважины.

Технический результат, достигаемый при реализации изобретения, заключается в обеспечении возможности одновременного получении информации о свойствах относительно толстого (около 1 м) слоя пород вокруг скважины и информации о теплопроводности пород для всего цементируемого интервала глубин; кроме того, он не требует подвода в скважину электрической энергии.

Указанный технический результат достигается тем, что в соответствии с предлагаемым способом определения профиля теплопроводности горных пород в скважину опускают обсадную колонну с прикрепленными на ее наружную поверхность датчиками температуры, закачивают цемент в кольцевой зазор между обсадной колонной и стенками скважины, в процессе закачки и затвердевания цемента осуществляют измерения температуры и определяют теплопроводность окружающих скважину горных пород по формуле

λ ( z ) = Q c ⋅ V a ( z ) 4 π ⋅ C ( z )

где λ(z) - теплопроводность пород на глубине z, Q_c - тепло гидратации цемента, V_a(z) - объем кольцевого зазора, приходящийся на метр длины скважины, на глубине z, C(z) - коэффициент, определяемый методом линейной регрессии при аппроксимации зависимости измеренной в скважине температуры T(z,t) от обратного времени t^-1 асимптотической формулой

T(z,t)=T_ƒ(z)+C(z)·t^-1,

где T_ƒ(z) - температура пород на глубине z.

В качестве датчиков температуры может быть использован оптико-волоконный датчик.

Изобретение поясняется чертежами, где на фиг.1 приведена геометрия цилиндрически симметричной модели, которая использовалась при расчетах, на фиг.2 - результаты численного моделирования зависимости температуры цемента от обратного времени, прошедшего после начала гидратации для двух значений теплопроводности пород.

Как показано на фиг.1, в соответствии с предлагаемым изобретением для температурного мониторинга процесса закачки и затвердевания (гидратации) цемента и последующего температурного мониторинга добычи нефти/газа или закачки флюида 1 в скважину, окруженную породой 4, опускают обсадную колонну 2 с прикрепленным к ней кабелем волоконного измерителя 5 температуры.

Во время гидратации цемента 3, закаченного в кольцевой зазор между обсадной колонной 2 и стенками скважины, происходит выделение значительного количества тепла (Q_c=100÷200 МДж на 1 м³ цементного раствора). Максимальное увеличение температуры во время затвердевания цемента составляет приблизительно 20-50°С. Основная стадия гидратации цемента (и выделения тепла) имеет продолжительность 30-50 часов, после чего радиус области, имеющей повышенную температуру, увеличивается и температура в скважине релаксирует к невозмущенной температуре пород на рассматриваемой глубине.

Скорость релаксации температуры зависит от количества избыточной тепловой энергии Q, приходящейся на 1 м длины скважины, и тепловых свойств пород, окружающих скважину. Избыточную тепловую энергию Q можно найти, как произведение измеренного в лаборатории тепла гидратации цемента Q_c и объема кольцевого зазора, который определяется внешним радиусом обсадной колонны r_co и измеренным с помощью калипера радиусом скважины, зависящим от глубины z: r_w(z). Таким образом, скорость восстановления температуры в скважине после цементации определяется исключительно тепловыми свойствами окружающих пород.

Ниже приведена теоретическая модель, которая используется как основа для определения тепловых свойств пород по измеренной в скважине зависимости температуры от времени.

Известно решение цилиндрически симметричной задачи кондуктивной теплопроводности об эволюции во времени произвольного начального распределения температуры в однородной среде (см., например, Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964, с.88). В частном случае начального распределения температуры, имеющего форму цилиндра,

зависимость от времени температуры в центре этого цилиндра имеет вид

где r₀ есть радиус цилиндра, ′а′ есть температуропроводность среды.

При достаточно больших временах после начала релаксации температуры ( t > > 2 ⋅ r 0 2 / a ) экспонента в формуле (2) может быть разложена в ряд и выражение для температуры на оси цилиндра примет вид

Эта формула может быть записана в виде общего закона сохранения энергии (путем умножения числителя и знаменателя (3) на множитель π·ρс):

где Q = π r 0 2 ⋅ ρ c ⋅ Δ T 0 есть количество избыточной тепловой энергии в среде, λ и ρc - теплопроводность и объемная теплоемкость среды.

Численные эксперименты показывают, что обобщенная асимптотическая формула (4) справедлива при любом виде начального распределения температуры. При этом r₀ есть характерный размер области, в которой начальная температура существенно отличается от температуры окружающей среды, и требуется выполнение условия:

t > > 2 ⋅ r 0 2 a                                                                  (5)

Формула (4) показывает, что если начальное тепловое возмущение в цилиндрически симметричной задаче задавать в виде количества избыточной тепловой энергии в однородной среде, то асимптотическое поведение температуры определяется исключительно теплопроводностью среды.

В рассматриваемом случае среда гетерогенна (Фиг.1): скважинный флюид (0<r<r_ci, r_ci - внутренний радиус обсадной колонны), обсадная колонна (r_ci<r<r_co, r_co - внешний радиус обсадной колонны), цемент (r_co<r<r_w, r_w - радиус скважины) и порода (r_w<r), имеет существенно разные тепловые свойства. Тем не менее, как показывают численные расчеты, асимптотическая формула (4) достаточно точно описывает изменение скважинной температуры со временем. Это объясняется тем, что при больших временах увеличение радиуса нагретой области определяется исключительно теплопроводностью пород, а радиальные вариации температуры вблизи скважины невелики.

В рассматриваемом случае избыточная тепловая энергия Q определяется произведением тепла гидратации цемента Q_c(J/m³) и объема кольцевого зазора V_a (м³ на один метр длины скважины)

Q ( z ) = Q c ⋅ V a ( z )                                                      (6)

V a ( z ) = π L ⋅ ∫ z − L 2 z + L 2 ( r w ( z ) 2 − r c o 2 ) d z                                  (7)

где L есть интервал глубин, который используется для усреднения объема кольцевого зазора. Типичная величина этого параметра L=2÷3 м, она дает вертикальную разрешающую способность предлагаемого метода. Величина L определяется сглаживающим эффектом вертикальной кондуктивной теплопередачи в породе и типичным временем проведения измерений.

Если невозмущенная температура T_ƒ(z) пород на рассматриваемой глубине z известна, то теплопроводность пород λ(z) определяется значением функции F(z,t) при больших временах (t>t₀):

Q c ⋅ V a ( z ) 4 π ⋅ t ⋅ [ T D T S ( z , t ) − T ƒ ( z ) ] = F ( z , t )     ⇒ t > t m     λ ( z )                                  (8)

Время t_m должно быть больше продолжительности основной стадии гидратации цемента и времени, при котором становится применима асимптотическая формула (4). Типичное значение t_m=100-150 часов.

Обычно невозмущенная температура пород T_ƒ(z) неизвестна и теплопроводность пород предлагается находить следующим образом.

Измеренные значения температуры при t>t_m аппроксимируют асимптотической формулой (при времени гидратации более 100 часов)

При этом методом линейной регрессии находят параметр C(z) и температуру пород T_ƒ(z), которая не используется при последующем расчете теплопроводности.

Параметр C используют для расчета теплопроводности пород по формуле:

λ ( z ) = Q c ⋅ V a ( z ) 4 π ⋅ C ( z )                                                     (10)

Предлагаемый способ определения теплопроводности пород был проверен на синтетических случаях, подготовленных в помощью коммерческого симулятора Comsol. Геометрия цилиндрически симметричной модели, которая использовалась при расчетах, приведена на Фиг.1.

Внутренние и внешние радиусы обсадной колонны равны r_ci,=0.1 м, r_co=0.11 м, радиус скважины r_w=0.18 м, внешний радиус расчетной области r_e=20 м. Использованные при расчетах тепловые свойства скважинного флюида (приведено эффективное значение теплопроводности, учитывающее свободную тепловую флюида), обсадной колонны, цемента и породы приведены в таблице.

	ТС, Вт/(м·К)	ρ, кг/м3	С, Дж/(кг·К)
Флюид	3 (эффективное значение)	1000	4000
Колонна	30	7800	500
Цемент	0.8	2600	900
Порода	1 и 2	2700	1000

Использовалась следующая аналитическая формула для мощности тепловыделения при гидратации цемента q(t):

q ( t ) = Q π ⋅ t 1 ⋅ exp [ − ( t − t 0 t 1 ) 2 ] , Q c = ∫ 0 ∞ q ( t ) d t

Вычисления проводились для следующих параметров, характеризующих тепловыделение при гидратации цемента: Q_c=1.5·10⁸ J/m³, t₀=6 час, t₁=8 час.

На Фиг.2 приведена расчетная зависимость температуры в кольцевом зазоре на расстоянии 0.13 м от оси скважины от обратного времени t^-1, с^-1 (интервал времени 300-100 часов с начала гидратации цемента) для двух значений теплопроводности пород: λ=1 и 2 Вт/м·К. Уравнения регрессии и белые линии соответствуют линейной аппроксимации результатов численного моделирования. Начальная температура принималась равной нулю. В приведенном интервале времени расчетные зависимости хорошо описываются прямыми линиями (9). Показанные на фигуре уравнения регрессии имеют близкие к нулю свободные члены (0.0283 и 0.0473), что соответствует нулевой начальной температуре, а подстановка в уравнение (10) коэффициентов уравнения регрессии (С(1 Вт/м·К)=703030 и С(2 Вт/м·К)=387772) дает следующие значения теплопроводности пород: 1.07 и 1.96 Вт/м·К.

Можно увеличить точность определения теплопроводности пород и существенно уменьшить необходимую продолжительность измерения температуры, если для решения обратной задачи использовать численное моделирование процесса гидратации цемента в скважине.

1. Способ определения профиля теплопроводности горных пород в скважине, в соответствии с которым в скважину опускают обсадную колонну с прикрепленными на ее наружную поверхность датчиками температуры, закачивают цементный раствор в кольцевой зазор между обсадной колонной и стенками скважины, в процессе закачки и затвердевания цемента осуществляют измерения температуры и определяют теплопроводность окружающих скважину горных пород по формуле λ ( z ) = Q c ⋅ V a ( z ) 4 π ⋅ C ( z ) где λ(z) - теплопроводность пород на глубине z, Q_c - тепло гидратации цемента, V_a(z) - объем кольцевого зазора, приходящийся на метр длины скважины на глубине z, C(z) - коэффициент, определяемый методом линейной регрессии при аппроксимации зависимости измеренной в скважине температуры T(z,t) от обратного времени t^-1 асимптотической формулойT(z,t)=T_f(z)+C(z)·t^-1,где T_f(z) - температура пород на глубине z.

2. Способ по п.1, в соответствии с которым в качестве датчиков температуры используют оптико-волоконный датчик.

3. Способ по п.1, в соответствии с которым для определения теплопроводности пород используют численное моделирование процесса гидратации цемента в скважине.