Способ восстановления температурно-временных условий генезиса алмаза

Способ восстановления температурно-временных условий генезиса алмаза

Иллюстрации

Показать все

Реферат

Изобретение относится к физико-химическим методам анализа и может быть использовано при научной и коммерческой экспертизе алмазов типа IaAB, либо смешанного типа Ib-IaA.

Как известно [1, 2], примесный азот преимущественно присутствует в алмазе в виде следующих 3-х основных типов центров, концентрации которого в этих центрах могут быть определены, например, методом ИК-спектроскопии по поглощению в однофононной (0÷1332 см^-1) области спектра [3, 4, 5]: С-центр представляет собой диспергированные атомы одиночного азота в замещающих позициях алмазной решетки, А-центр - пара азотных атомов в замещающем положении ближайших соседей [6] и В-центр - четыре замещающих азотных атома, окружающих вакансию. Согласно принятым в настоящее время представлениям об эволюции азотных центров в алмазе, примесный азот, первоначально внедряющийся в процессе роста кристалла алмаза в виде одиночных атомов, сначала агрегируется с образованием A-центров. Дальнейший процесс агрегации A-центров, при достаточной для его осуществления температуре, приводит к образованию В-центров. Поскольку степень агрегации азота в алмазе зависит от температурно-временной истории его ростового и постростового периода, представляется возможным использование количественных характеристик кинетики агрегации азотных C- и A-центров в алмазе для восстановления температурно-временных условий его генезиса.

Аналогом способа оценки температурно-временных условий генезиса природных кристаллов по содержанию в них примесного азота может служить работа [7]. В данной работе впервые осуществлена попытка оценки температурно-временных условий пребывания природных алмазов в верхней мантии по степени агрегации азота в кристаллах типа Ib-IaA и IaAB, на основе результатов проведенных экспериментов по отжигу этих кристаллов в лабораторных условиях. Примененный авторами способ определения допустимых пар значений температуры и продолжительности пребывания в верхней мантии природных алмазов с заданной степенью агрегации азотных C-, либо A-центров справедлив для локальной области кристалла в изотермической модели.

Способ недостаточно достоверен для определения температурно-временной истории генезиса конкретного образца. Полученные авторами численные оценки не отражают температурно-временной истории конкретного кристалла, а являются модельной оценкой для абстрактного образца, имеющего всюду внутри себя одинаковую концентрацию азота и степень его агрегации. Такая ситуация никогда не наблюдается в алмазных пластинах согласно результатов исследований в них распределения концентраций азота.

Наиболее близким примером использования количественной оценки содержания азотных центров для анализа температурно-временных условий генезиса природных алмазов является приведенный, например, в работах [2, 8, 9, 10] способ оценки температуры и продолжительности пребывания природного алмаза в мантии. Способ основан на вычислении из локальных концентраций примесного азота в формах C, A и B в кристалле, измеренных методом ИК-спектроскопии, локального численного значения эмпирического интегрального параметра кинетики агрегации n-го порядка K_n×t соответствующих азотных центров и дальнейшее определение из него допустимых пар значений температуры и времени пребывания кристалла в мантии. Данный способ основан на использовании для описания процесса агрегации азотных центров уравнения кинетики n-го порядка

С - концентрация агрегирующих центров;

n - предполагаемый порядок кинетики агрегации;

K_n - константа скорости реакции агрегации азотных центров;

где константа K_n, в свою очередь, определяется уравнением Аррениуса

E_a и A_r - энергия активации и постоянная Аррениуса, вычисляемые из определяемых экспериментально значений константы скорости реакции агрегации K_n соответствующих азотных центров при нескольких различных температурах;

k_B - постоянная Больцмана;

T - абсолютная температура.

Всеми предыдущими авторами предполагалось, что температура T в константе скорости реакции агрегации K_n (2) остается постоянной. Физически это предположение означает, что на протяжении всего времени пребывания алмаза в верхней мантии, до его извержения на земную поверхность, температура среды его пребывания оставалась приблизительно одинаковой. Связь между концентрациями азотных центров и температурно-временными условиями процесса агрегации устанавливалась путем интегрирования уравнения (1)

При постоянной температуре, интегрирование правой части (3) дает произведение константы K_n на время t пребывания алмаза в мантии.

Выражения, связывающие концентрации C₀ и C_t агрегирующих азотных центров с константой скорости реакции агрегации K_n и временем агрегации t, имеют вид

t - продолжительность отрезка времени, в течение которого происходила агрегация;

С₀ и С_t - начальная и конечная концентрации соответствующих агрегирующих центров.

Численные значения констант E_a и A_r в Kn, а также размерность A_r, при их экспериментальном определении, зависят от рассматриваемого порядка n. Численное значение порядка кинетики n определяется применяемой при расчетах моделью механизма агрегации. В экспериментах [2] по высокотемпературному отжигу алмазов были определены численные значения постоянных A_r и E_a для процесса агрегации C-центров при n=2 и для процесса агрегации A-центров при n=2; 1,5; 1,0. Показано, что для процесса агрегации C-центров в форму А наиболее приемлемым является 2-й порядок кинетики агрегации [2, 11]. Для процесса агрегации A-центров в форму B также большинством авторов [2, 9] использовался 2-й порядок, который соответствует модели агрегации азотных центров по диффузионному механизму. Есть также примеры использования для анализа экспериментальных данных кроме 2-го и других порядков, например n=1,5 в [8]. В частности, для кинетики 2-го порядка из (4) получается следующее уравнение, связывающее данные по концентрации азотных центров с температурой и временем пребывания алмаза в мантии.

Данное соотношение в большинстве случаев и являлось основой для оценок температурно-временных характеристик генезиса алмаза в упомянутых работах. Численные значения концентраций азотных центров в алмазе C₀ и C_t для расчета левых частей уравнений (4) и (5), как правило, вычислялись по данным ИК-спектроскопии. Локальные концентрации азота в азотных центрах C, A и B определяли по стандартной процедуре пересчета при помощи принятых в научной литературе коэффициентов [3, 4], связывающих концентрации азота в этих центрах с коэффициентами поглощения на характерных для этих центров частотах. Поскольку в правой части уравнения (6) содержатся два неизвестных - температура T и время t, то оценка предыдущими авторами температурно-временных условий генезиса природных алмазов осуществлялась на основе дополнительного предположения либо о продолжительности времени t пребывания природных алмазов из конкретного коренного источника в верхней мантии, либо о температуре среды пребывания, которая в обоих случаях полагалась постоянной для конкретной области кристалла. В первом случае предполагаемые отрезки геологического времени пребывания алмаза в верхней мантии составляли, как правило, величину в интервале приблизительно от 0,1 до 3 миллиардов лет, в зависимости от тех или иных конкретных геологических условий, после чего из соотношения (6) определялась температура генезиса кристаллов T. Такие расчеты приводили к значениям температуры генезиса природных алмазов в диапазоне (900÷1300)°C, в зависимости от концентрации и степени агрегации азота в кристаллах. Аналогичным способом из того же соотношения (6) оценивали время пребывания алмаза в верхней мантии, исходя из предположения о температуре среды пребывания, как правило, в районе 1200°C.

Начиная с первых расчетов, связанных с геофизическими факторами генезиса кристаллов алмаза [7, 9], все авторы находились в рамках одной и той же расчетной модели равенства температуры пребывания алмаза в верхней мантии и температуры его роста. Поэтому за прототип изобретения можно выбрать более позднюю работу [8], т.к. в ней была предпринята попытка интерпретировать данные по ИК-профилированию на пластинах из природных алмазов с точки зрения величины параметра K_n×t при различных значениях порядка кинетики агрегации A-центров. В данной работе проведены исследования по генезису 124 алмазов, извлеченных из ксенолита кимберлитовой трубки Удачная. Для исследования внутреннего строения кристалла из имеющейся коллекции были отобраны кристаллы различной морфологии. Из них были приготовлены плоскопараллельные пластинки толщиной (100÷200) мкм. Примесный состав алмазов исследовался методами ЭПР, фотолюминесценции и ИК - спектроскопии. Авторами, в результате проведенных исследований, сделан вывод о том, что образование алмазов происходило в два этапа с локальными вариациями механизма их роста: на первом этапе образовались октаэдры (имеют большие значения параметра Kn×t в центральной части), затем после длительного пребывания в мантии сформировались внешние зоны на алмазах первой генерации и происходило формирование кристаллов «смешанного» кубоктаэдрического габитуса (малые значения параметра Kn×t в периферийной части октаэдров и у кубоктаэдров). Далее, на основе изотермической модели, определялись допустимые значения времени пребывания при заданной температуре для этих частей, которые отличались по продолжительности отжига пропорционально параметру Kn× t. Авторы получили отношения этих продолжительностей равными 30 и 14 для значения порядка кинетики агрегации n, равного 2 и 1,5 соответственно. Максимальные общие продолжительности пребывания алмазов в верхней мантии при температуре 1150°C, полученные авторами для данных значений порядка кинетики, равны соответственно 1430 млн. лет и 590 млн. лет для центральной части и 110 млн. лет и 22 млн. лет для периферийной части.

Общим недостатком известных способов является малая достоверность определения температуры роста кристалла и температуры его пребывания в верхней мантии на основе предположения о неизменной температуре процесса алмазогенеза. Например, при интерпретации экспериментальных результатов в работе [8] авторы также исходят из предположения об одинаковости температуры роста кристалла и температуры его пребывания в верхней мантии. Из него следует, что временной масштаб непрерывного процесса роста участков кристалла имеет геологический масштаб времени. Например, уменьшение параметра Kn×t по микрослоям роста кристалла в его периферийной части будет означать, что непрерывное во времени нарастание этих микрослоев продолжалось миллионы, либо десятки миллионов лет, поскольку, полученные авторами продолжительности пребывания в верхней мантии при температуре 1150°C для периферийной части составляют 110 млн. лет для порядка кинетики n, равном 2, и 22 млн. лет - для порядка кинетики 1,5. Такая продолжительность непрерывного роста не выдерживает критики с точки зрения возможных минимальных скоростей нарастания грани кристалла.

На основе проведенного автором анализа данных по ИК-профилированию и ИК-картированию (фиг.1, фиг.2, 6 (и, к)) содержания азота в алмазных пластинах установлено, что изотермическая модель пребывания алмаза в верхней мантии встречается с непреодолимыми затруднениями в интерпретации получаемых результатов, при их пересчете по формуле (6). Затруднения вызваны тем фактом, что суммарное значение временных интервалов процесса роста алмаза в мантии неизмеримо меньше общего времени его пребывания в ней до извержения на земную поверхность, поскольку последнее по порядку величины является геологическим. Из этого следует, что при неизменности температуры среды пребывания алмаза в верхней мантии, прибавка в величине вычисляемого из левой части формулы (6) локального численного значения эмпирического интегрального параметра кинетики агрегации n-го порядка K_n×t, приобретаемая за время роста кристалла, должна быть неизмеримо меньше тех его изменений, на которые увеличивался этот параметр за те периоды, когда кристалл не рос. Следовательно, неизменность температуры пребывания алмаза в мантии должна была бы привести к совершенно определенному распределению локальных значений параметра K_n×t по кристаллу. А именно: этот параметр либо должен был бы быть везде внутри кристалла строго одинаковым, если во время его роста не было геологически продолжительных остановок, либо он должен был бы иметь строго ступенчатый характер, если такие остановки были. На практике же, в алмазных пластинах часто встречаются участки плавного уменьшения численного параметра K_n×t при перемещении от генетического центра кристалла к периферии (фиг.1г, 2г, 6к). Если предположить, что на этих участках кристалл рос непрерывно при неизменной температуре пребывания алмаза в верхней мантии, то время непрерывного роста такого участка должно составлять десятки или сотни миллионов лет, что не выдерживает критики с точки зрения теории роста кристаллов. Если же предположить, что это уменьшение состоит из большого числа очень мелких ступенек, то такой сценарий роста должен включать в себя огромное число равномерно распределенных во времени очень коротких промежутков роста, порядка нескольких часов или даже минут, перемежающихся промежутками остановок роста, длиной порядка нескольких десятков тысяч лет каждый. Вероятность такого сценария роста также бесконечно меньше вероятности обычной процедуры непрерывного роста кристалла. Отметим, что с момента выхода первых работ по кинетике агрегации азотных центров в алмазе, эмпирические константы, используемые при расчетах, непрерывно уточнялись, и, по всей видимости, будут уточняться и дальше.

Целью настоящего изобретения является повышение достоверности определения температурно-временных условий роста областей кристалла, а также определение, в рамках изотермической модели, температурно-временных условий периода постростового пребывания кристалла и температурно-временных условий задержек роста кристалла.

Поставленная цель достигается тем, что в способе восстановления температурно-временных условий генезиса алмазов типа IaAB, либо смешанного Ib-IaA типа, основанном на вычислении по локальным концентрациям примесного азота в формах C, A и B в кристалле, измеренным, например, методом ИК-микроспектроскопии, локальных значений интегрального параметра K_nt кинетики агрегации n-го порядка соответствующих азотных центров, определении температуры и времени генезиса, дополнительно регистрируют изменение значений интегрального параметра агрегации соответствующих азотных центров ΔK_nt по слоям роста кристалла, например, в какой-либо области тонкой алмазной пластины, пересекающей ростовые слои, а определение температуры T и времени Δt генезиса проводят из уравнения

где: k_B - постоянная Больцмана,

A_r и E_a - постоянная Аррениуса и энергия активации процесса агрегации C-, либо A-центров, соответствующие порядку кинетики агрегации n. Допустимые пары значений температуры T и продолжительности Δt непрерывного роста данной области кристалла определяют по величине монотонного и однородного уменьшения интегрального параметра агрегации Δ(K_nt) по слоям роста выбранной области.

Допустимые пары значений температуры T и продолжительности Δt постростового пребывания кристалла алмаза в изотермической модели определяют по значению интегрального параметра агрегации соответствующих азотных центров (K_nt)_пов вблизи участка внешней нерастворенной поверхности кристалла, где Δ(K_nt) принимается равным (K_nt)_пов.

Допустимые пары значений продолжительности Δt и температуры T задержки роста кристалла в изотермической модели определяют по величине скачкообразного уменьшения интегрального параметра агрегации Δ(K_nt), соответствующего внутренней границе задержки роста кристалла, причем в случае растворенного участка внутренней границы задержки роста, получаемые значения определяют верхнюю границу допустимой температуры T, сопровождаемого растворением изотермического процесса задержки роста кристалла, при выбранной продолжительности Δt, либо верхнюю границу допустимой продолжительности задержки Δt при выбранной температуре T.

Допустимые пары значений температуры T и продолжительности Δt постростового пребывания алмаза с растворенный внешней поверхностью в изотермической модели определяют по минимальному значению интегрального параметра агрегации (K_nt)_пов соответствующих азотных центров на исследуемом участке вблизи поверхности кристалла, при этом получаемые значения определяют верхнюю границу допустимой температуры T при выбранной продолжительности Δt изотермического процесса постростового пребывания кристалла, сопровождаемого растворением, либо верхнюю границу допустимой продолжительности постростового пребывания Δt при выбранной температуре T.

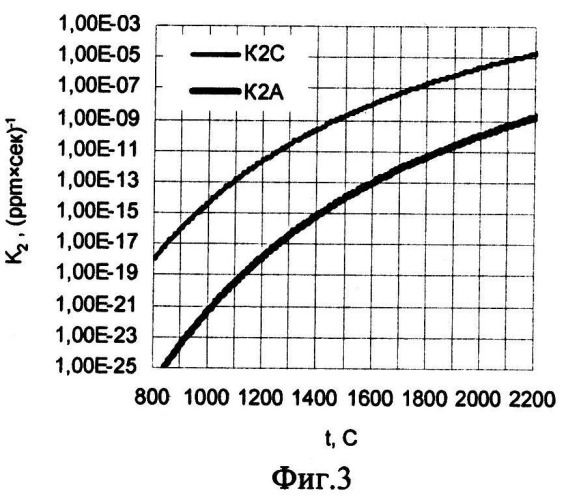
Принимая во внимание, что температура кристалла в течение его ростовой истории и постростового периода не обязательно остается постоянной, а может изменяться, а также то, что численное значение константы скорости реакции агрегации K_n очень сильно изменяется с изменением температуры (фиг.3), приходим к нижеследующему определению интегрального параметра агрегации азотных центров в алмазе K_nt. Численное значение параметра K_nt, вычисляемое из левой части уравнения (3) для данной локальной области кристалла, представляет собой функционал от температурной истории T(t) этой локальной области на протяжении всего времени t ее существования - от начала кристаллизации данной области и до момента измерения в ней концентрации азотных центров.

Здесь и в дальнейшем выражение K_nt уже не является произведением константы скорости реакции агрегации K_n на время t, как это показано в формулах (4) и (5), а представляет собой единый численный эмпирический параметр, называемый интегральный параметр агрегации азотных центров для данной локальной области кристалла с температурной историей T(t).

Поскольку температура алмаза во всех его частях в любой момент времени всегда одинакова, и таким образом, при отжиге кристалла все локальные значения интегрального параметра K_nt во всех частях кристалла будут увеличиваться на одну и ту же величину, независимо от исходного значения этого параметра в данной точке или значения локальной концентрации примесного азота, то можно сформулировать два важных, для дальнейшего анализа температурно-временных условий генезиса алмаза, свойства данного параметра, а именно:

1) интегральный параметр K_nt имеет одинаковые численные значения на любых изохронных поверхностях роста кристалла, поскольку температурная история T(t) для всех локальных областей кристалла, кристаллизовавшихся в одно и то же время, будет одинаковой;

2) значения интегрального параметра K_nt монотонно уменьшаются для каждой последующей во времени изохронной поверхности роста, по отношению к предыдущей, с сохранением неизменной во времени разности значений Δ(K_nt) данного параметра для любых двух локальных областей кристалла с отсчетами времени начала их кристаллизации t₁ и t₂ (t₂ больше t₁).

где T₁₂(t) - температурная история кристалла на отрезке времени от t₁ до t₂. В случае если на отрезке Δt, равном (t₂-t₁), температура кристалла T₁₂(t) остается постоянной во времени и равной T, то из формулы (10) мы получаем уравнение (7).

Второе свойство также следует из одинаковости температуры во всех точках кристалла, поскольку любая только что выкристаллизовавшаяся область кристалла на его поверхности, и имеющая значение K_nt, равное нулю, и любая внутренняя по отношению к ней локальная область кристалла, обладающая в этот момент неким ненулевым значением параметра агрегации, в дальнейшем обе будут абсолютно одинаково увеличивать значения своих параметров агрегации, так как с этого момента их температурные истории T(t) будут абсолютно одинаковы. Это означает, что пространственное распределение разницы значений интегрального параметра агрегации Δ(K_nt) по кристаллу не изменяется со временем, сколько бы кристалл ни отжигался после окончания его роста.

Сформулированные выше свойства интегрального параметра k_nt будут выполняться при условии, что величина энергии активации E_a в правой части формул (8) и (9) имеет неизменное значение по всему кристаллу. Известно, что изменение значения энергии активации возможно при помощи создания факторов, стимулирующих процесс агрегации азотных центров в алмазе, например, при помощи искусственного создания в кристалле вакансий либо путем осуществления роста в присутствии металлов катализаторов-растворителей углерода, например, никеля. Как следует из экспериментов по изучению кинетики агрегации азотных центров, данное условие неизменности значения E_a выполняется в изученных природных алмазах типа Ia и Ib, а также в синтетических кристаллах, не подвергавшихся воздействию факторов, стимулирующих агрегацию.

Два сформулированных выше свойства интегрального параметра K_nt позволяют использовать его в качестве универсального локального количественного генетического параметра, аккумулирующего в себе температурно-временную историю генезиса T(t) для данной локальной области. Данный параметр отслеживает пространственную картину роста кристалла, посредством изолиний его значений для последовательных изохронных поверхностей роста, и фиксирует поверхности остановок роста и растворения - по скачкам его значений на этих поверхностях.

Особо ценной информацией обладает картина относительных изменений интегрального параметра ΔK_nt, приобретенных в процессе роста, вдоль выбранного направления от генетического центра к периферии.

Плавное, без ступенек, уменьшение параметра K_nt по слоям роста кристалла (фиг.1г) означает, что заметная агрегация азотных центров происходила одновременно с процессом непрерывного роста кристалла и при температуре, достаточной для увеличения этого параметра на измеримую величину за время роста данного участка. Наличие линейного участка уменьшения параметра K_nt по слоям роста позволяет предположить, что температура, при которой рос кристалл, как и скорость нарастания грани, были приблизительно постоянны. При наблюдении подобного сценария, и исходя из толщины слоя d и известных литературных данных о допустимом диапазоне скоростей нарастания грани алмаза υ_n в соответствующих P-T условиях, можно оценить время Δt непрерывного роста такого участка, как d/υ_n. Измерив разницу значений Δ(K_nt) для изохронных поверхностей, ограничивающих такой ростовой слой, можно вычислить температуру кристаллизации данного слоя из уравнения (7). Конкретная реализация данного сценария приведена в примере 1, таблица 4.

В постростовой период локальные значения интегрального параметра агрегации в любой точке внутри кристалла увеличиваются в процессе постростового отжига на одинаковую величину. При этом численное значение интегрального параметра на поверхности кристалла (K_nt)_пов будет равняться постростовому увеличению интегрального параметра агрегации, поскольку его начальное значение в момент окончания роста кристалла равнялось нулю. В общем виде значение интегрального параметра на участке поверхности кристалла без признаков растворения записывается как

где T(t) - постростовая температурная история кристалла от момента начала его постростового пребывания t_нач, обусловленного окончанием процесса его роста, до момента измерения содержания азота в данной приповерхностной зоне кристалла t_кон. Если природный кристалл не подвергался отжигу в лабораторных условиях, то значение интегрального параметра на его поверхности (K_nt)_пов полностью определяется периодом его постростового пребывания в верхней мантии, поскольку после выброса кристалла на земную поверхность, изменения его интегрального параметра пренебрежимо малы, из-за очень резкой зависимости константы агрегации от температуры (фиг.3). Реальную температурную историю постростового пребывания алмаза в верхней мантии восстановить невозможно, но можно оценить продолжительность его постростового пребывания Δt, исходя из изотермической модели. В этом случае температура T(t) в правой части формулы (11) на отрезке времени Δt, равном (t_кон-t_нач), остается постоянной, и мы получаем из формулы (11) уравнение (7), где в правой части, в качестве изменения Δ(K_nt) интегрального параметра агрегации в постростовой период, стоит его значение (K_nt)_пов вблизи участка внешней нерастворенной поверхности. Таким образом, допустимые пары значений температуры T и времени Δt для периода постростового пребывания кристалла определяют из уравнения (7), полагая значение Δ(K_nt) в правой части уравнения равным значению интегрального параметра агрегации (K_nt)_пов вблизи участка внешней нерастворенной поверхности кристалла. Данный случай описан в примере 2 и таблице 5.

В случае выявления внутренней границы задержки роста кристалла, измеряют величину скачкообразного уменьшения интегрального параметра агрегации Δ(K_nt) в данной локальной области внутренней границы задержки роста и из формулы (7) определяют допустимые пары значений продолжительности Δt и температуры T для изотермической модели задержки роста данного участка. Причем, в случае растворенной границы задержки роста, полученные пары значений T и Δt означают верхнее граничное значение температуры T при выбранной продолжительности, сопровождаемого растворением процесса изотермической задержки Δt роста кристалла, либо верхнее граничное значение длительности задержки роста Δt при выбранной температуре T. Данный случай описан в примере 3 и таблице 7.

При измерении интегрального параметра агрегации (K_nt)_пов вблизи участка внешней растворенной поверхности кристалла также можно вычислить из уравнения (7) допустимые пары значений температуры Е и продолжительности Δt изотермического постростового пребывания кристалла, сопровождаемого процессом растворения поверхности. В этом случае значение интегрального параметра агрегации вблизи поверхности будет включать в себя, кроме вклада, обусловленного собственно постростовым отжигом - формула (11), также вклад растворенной части, равный разнице значений интегральных параметров агрегации Δ(K_nt) по краям растворенного слоя на момент начала процесса растворения - формула (10). Погрешность определения температурно-временных параметров изотермического постростового отжига в этом случае будет определяться долей вклада Δ(K_nt) растворенной части, по отношению к вкладу, обусловленному собственно изотермическим постростовым отжигом. При исследовании участка растворенной внешней поверхности выбирают минимальное значение интегрального параметра для данного участка, как соответствующее минимальному вкладу растворенной части, и из уравнения (7) вычисляют допустимые пары значений температуры и времени изотермического постростового пребывания, которые определяют верхнюю границу допустимой температуры сопровождаемого растворением изотермического процесса постростового пребывания кристалла T, при выбранной продолжительности пребывания Δt, либо верхнюю границу допустимой продолжительности постростового пребывания Δt при выбранной температуре T. Данный случай описан в примере 4 и таблице 8. Предлагаемый способ поясняется на фиг.1-6, где:

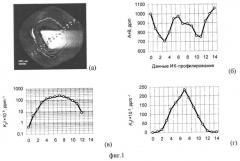
фиг.1

(а) - точки ИК-профилирования алмазной пластины с выбранным профилем измерений (точки 0÷14) по слоям роста. Визуализация структуры поверхности осуществлена методом катодолюминесценции. Расстояние между точками измерения составляет около 100 мкм;

(б) - данные ИК-профилирования. Значения концентраций суммарного азота в формах A и B в точках измерения, полученные методом ИК-микроспектроскопии;

(в) - локальные значения интегрального параметра агрегации A-центров K₂t×10⁵ в точках измерения в логарифмическом масштабе;

(г) - значения интегрального параметра агрегации K₂t×10⁵ в точках измерения в обычном масштабе;

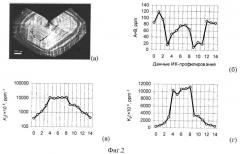
фиг.2

(а) - точки ИК-профилирования алмазной пластины, вырезанной в плоскости (110). Расстояние между точками измерения около 100 мкм. Визуализация структуры поверхности пластины на фото осуществлена методом катодолюминесценции;

(б) - распределение концентрации общего азота в формах A и B по точкам ИК-профилирования;

(в) - локальные значения интегрального параметра агрегации A-центров K₂t×10⁵ в точках ИК-профилирования в логарифмическом масштабе;

(г) - значения интегрального параметра агрегации K₂t×10⁵ в точках ИК-профилирования в обычном масштабе;

фиг.3

зависимость констант скорости реакции агрегации K2C и K2A от температуры (формула (2), численные константы взяты из работы [2]):

K2C - расчет для процесса агрегации C-центров в форму A;

K2A - расчет для процесса агрегации A-центров в форму B;

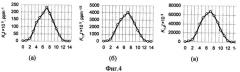
фиг.4

значения интегрального параметра агрегации A-центров K_nt×10⁵ для траверзы ИК-профилирования в алмазной пластине, изображенной на фиг.1 (а, б), при значениях порядка кинетики агрегации n, равных: (а) n=2,0; (б) n=1,5; (в) n=1,0;

фиг.5

(а) - алмазная пластина (110) толщиной около 0,4 мм. Ростовая история проявлена методом катодолюминесценции;

(б) - целый кристалл с растворенной поверхностью до его разрезания. Фото демонстрирует фотолюминесценцию алмаза при облучении лазерным светом 337 нм;

(в) - топограмма точек измерения (более 1000) локальных значений концентрации азота в алмазной пластине. Численная разметка по осям дана в микрометрах;

(г) - вычисленные значения интегрального параметра агрегации азотных А-центров в точках измерения,

фиг.6

(а-з) - значения интегрального параметра агрегации в точках измерения вблизи разных участков внешней поверхности. Минимальное значение ~50 ppm^-1 достигается в точке на фиг.6 (д, е);

(и, к) - линейный характер уменьшения интегрального параметра агрегации K_2At×10⁵ по слоям роста в периферийной части кристалла.

Способ осуществляется следующим образом.

Пример 1

В качестве примера рассмотрим анализ температурно-временных условий роста природного алмаза, исходя из данных по содержанию азота в пластине, приведенной на фиг.1. Как упоминалось выше, при анализе температурно-временных условий генезиса алмазов авторами обычно использовался 2-й порядок кинетики агрегации A-центров. Мы продемонстрируем расчет для всех трех порядков 2, 1,5 и 1, для которых в работе [2] приведены эмпирические значения констант скорости реакции агрегации при различных температурах и рассчитанные из них значения констант E_a (табл.1).

Константы скорости реакции агрегации K_nA для различных порядков (n=2; 1,5; 1) кинетики агрегации A-центров и рассчитанные из них значения энергии активации E_a [2] и постоянной Аррениуса A_r.

Таблица 1
Порядок агрегации n	Константы скорости реакции агрегации KnA азотных A-центров при двух температурах	Энергия активации Ea, eV	Постоянная Аррениуса Ar
(2600±100)°C	1130°C
2	(7±2)×10-6 ppm-1 min-1	6,8×10-18 ppm-1 min-1	6,53±0,04	3,40×104 ppm-1 sec-1

1,5	(1,3±0,5)×10-4 ppm-1/2 min-1	4,15×10-17 ppm-1/2 min-1	6,8±0,04	1,84×106 ppm-1/2 sec-1
1	(2,46±1)×10-3 min-1	2,53×10-16 min-1	7,07±0,04	1,02×108 sec-1

1. Осуществляем измерение концентраций азота в at. ppm по точкам выбранного профиля 0÷14 и записываем полученные данные концентраций азота для всех зафиксированных типов азотных центров в таблицу 2 (колонки 2 и 3). Расстояние между точками измерения ~100 мкм. [A] и [B] - измеренные концентрации азота в форме A и B, выраженные в at. ppm.

Таблица 2 Данные измерений концентраций азота в формах A и B и рассчитанные значения параметра KnA×105 для трех значений порядка кинетики агрегации n в точках 0÷14 ИК-профиля для алмазной пластины на фиг.1
№№ пп	Концентрация	Концентрация	n=2	n=1,5	n=1
[A], at. ppm	[B], at. ppm	K2At×105, ppm-1	K1,5At×105, ppm-1/2	K1,0At×105
1	2	3	4	5	6
0	998	2	0,40	8,96	188
1	828	14	4,02	82,06	1579
2	716	42	15,48	297,02	5373
3	573	131	64,95	1155,89	19437
4	529	275	129,32	2322,42	39507
5	533	410	163,15	3040,65	53802
6	502	470	192,65	3551,70	62318
7	437	454	233,20	4054,61	67265
8	485	409	188,66	3383,55	57712
9	542	323	137,79	2532,19	44096
10	577	187	84,84	1542,01	26489
11	648	103	42,33	790,03	13913
12	890	27	6,62	140,62	2811
13	997	0	0,00	0,00	0
14	1055	0	0,00	0,00	0

2. Поскольку, согласно полученным данным, исследуемый алмаз принадлежит типу IaAB, вычисляем по формулам (8) и (9) значения интегрального параметра K_nAt агрегации A-центров в точках измерения при порядках кинетики агрегации n, равных 2, 1,5 и 1 (таблица 3). При этом, значения конечных C_t и начальных C₀ концентраций азотных A-центров, выраженные в ppm, будут равны соответственно [A]/2 и ([A]+[B])/2, поскольку, согласно принятой модели A-центра [6], он состоит из двух атомов азота. Заносим полученные значения K_nAt×10⁵ в таблицу 2 (колонки 4, 5 и 6). Масштабный коэффициент 10⁵ выбран для удобства представления численных данных.

Таблица 3 Формулы для расчета интегрального параметра агрегации KnAt азотных A-центров при трех различных значениях порядка кинетики агрегации n
n=2	n=1,5	n=1,0

3. Наносим на графики рассчитанные в точках профиля 0÷14 значения K_nt×10⁵, фиг.1(г) и 4(а, б, в). Как видно из графика на фиг.1(г), для порядка кинетики n, равного 2, наблюдается продолжительный линейный участок 7÷12 уменьшения величины параметра K_2At×10⁵ от 233,2 ppm^-1 до, практически, нулевого значения. Измеренное значение параметра K_2At×10⁵ для максимально близкого к поверхности участка кристалла (точка 0) составляет приблизительно 0,4 ppm^-1.

Для оценки температуры роста по линейному участку уменьшения интегрального параметра агрегации, выбираем интервал между точками 8 и 11, соответствующий слою непрерывного роста кристалла, толщиной d приблизительно 300 мкм.

4. Осуществляем оценку температуры роста по линейному участку уменьшения параметра K_nt×10⁵ на выбранной траверзе, исходя из уравнения (7).

A_rexp(-E_a/k_BT)×Δt=Δ(K_nt)

Используя данные, приведенные в таблица 2 (строки 8, 11, колонки 4, 5, 6), вычисляем разницу значений интегрального параметра агрегации Δ(K_nt) для крайних поверхностей выбранного слоя 8÷11 при трех значен