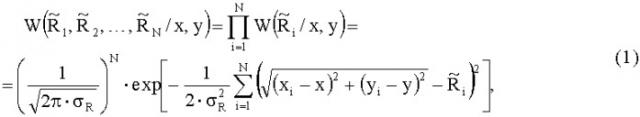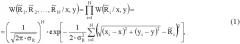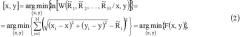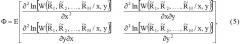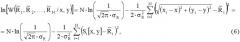Способ определения координат неподвижного радиомаяка с активным ответчиком

Способ определения координат неподвижного радиомаяка с активным ответчиком

Иллюстрации

Показать все

Реферат

Изобретение используется в радиотехнике.

Известны способы, которые могут быть использованы для определения координат неподвижного радиомаяка с активным ответчиком:

1. Способ определения координат [1, 2], реализующий разностно-дальномерный метод. Такой способ заключаются в приеме и измерении разностей задержек сигнала источника радиоизлучения (ИРИ) в пунктах приема с известным местоположением, решении гиперболических уравнений на центральном приемном пункте и вычислении на этой основе координат ИРИ.

Недостатком данного способа является необходимость использования минимум трех измерительных пунктов и системы связи между ними, при этом все измерения должны производиться одновременно, и, как следствие, необходимо использовать достаточно сложную систему единого времени, что затрудняет реализацию данных технических решений.

2. Способ определения координат разностно-доплеровским методом [3, с.246…248]. Сущность способа заключается в приеме сигнала ИРИ на двух перемещающихся измерителях, ретрансляции сигналов на центральный пункт обработки, вычислении разности доплеровских частот и разности радиальных скоростей измерителей с последующим вычислением координат ИРИ по разности доплеровских частот и разности радиальных скоростей.

Недостаток данного способа - необходимость использования не менее двух измерительных пунктов, кроме того, данные пункты должны перемещаться с достаточно большой скоростью, и данный способ не позволяет измерять координаты ИРИ, излучающих непрерывные или квазинепрерывные сигналы, т.к. в данном случае нельзя точно измерить разность частот сигнала [3, с.251].

Из известных способов определения координат неподвижного радиомаяка с активным ответчиком по технической сущности наиболее близким аналогом (прототипом) предлагаемого способа является способ, реализующий дальномерный метод [3, с.220…228], который включает посылку сигналов запроса передатчиками не менее чем с двух наземных пунктов, переизлучение сигналов запроса передатчиком ответчика на радиомаяке, координаты которого надо определить, измерение дальностей от наземных пунктов до радиомаяка R₁ и R₂ по величине задержки сигнала ответчика относительно сигналов запросчика и вычисление координат ответчика, как точки пересечения окружностей с радиусами R₁ и R₂, центры которых находятся в местах расположения запросчиков.

Недостатки способа прототипа:

1. Для реализации дальномерного метода определения координат неподвижного радиомаяка с активным ответчиком должно быть развернуто два и более стационарных наземных приемо-передающих пунктов (запросчиков).

2. При неизменной точности измерения дальностей для снижения ошибки определения координат радиомаяка с активным ответчиком необходимо увеличивать число стационарных приемо-передающих пунктов (запросчиков).

Целью настоящего изобретения является разработка способа, обеспечивающего повышение точности определения координат неподвижного радиомаяка с активным ответчиком и снижение числа приемо-передающих пунктов, за счет применения перемещающегося единственного запросчика и выбора рациональной траектории его перемещения.

Поставленная цель достигается тем, что в известном способе определения координат неподвижного радиомаяка с активным ответчиком, включающем посылку сигнала запроса передатчиком запросчика, прием и переизлучение сигнала запроса ответчиком на радиомаяке, согласно изобретению излучение сигнала запроса осуществляют перемещающимся передатчиком запросчика в N точках с координатами [x_i,y_i],  i = 1,N ¯ , измерение совокупности дальностей R ˜ i , i = 1,N ¯ по величине задержки сигнала ответчика относительно сигнала запросчика выполняют в каждой из N точек измерения на траектории перемещения запросчика, причем траектория перемещения запросчика выбирается так, чтобы угол между направлениями от возможного местоположения радиомаяка на крайние точки траектории перемещения был больше 180°, а вычисление координат [x,y] неподвижного радиомаяка с активным ответчиком осуществляется путем определения аргументов минимизации функции F(x,y):

[ x ,   y ] = arg min 〈 x ,  y 〉 { F ( x, y ) } = arg min 〈 x ,  y 〉 { ∑ i = 1 N ( ( x i − x ) 2 + ( y i − y ) 2 − R ˜ i ) 2 } ,

где F ( x ,  y ) = ∑ i = 1 N ( ( x i − x ) 2 + ( y i − y ) 2 − R ˜ i ) 2

Сопоставительный анализ с прототипом показывает, что заявляемый способ отличается введением новой операции - перемещения запросчика по заданной траектории (так, чтобы угол между направлениями от возможного местоположения радиомаяка на крайние точки траектории перемещения был больше 180°). Таким образом, заявляемый способ соответствует критерию изобретения «новизна».

Сравнение заявляемого способа с другими аналогичными способами показывает необходимость выполнения известных операций - посылку сигналов запроса передатчиком запросчика, прием и переизлучение сигналов запроса ответчиком радиомаяка, измерение дальности от запросчика до радиомаяка по величине задержки сигнала ответчика относительно сигнала запросчика. Однако перемещение измерителя дальности позволило сократить до одного количество запросчиков, а выбор заданной траектории перемещения дает возможность увеличить точность определения координат радиомаяка. Следовательно, можно сделать вывод о соответствии заявляемого способа критерию «существенные отличия».

Поясним подробнее сущность заявляемого способа.

Предположим, что неподвижный радиомаяк с активным ответчиком находится в заданной области двухмерного пространства. Обозначим через [x,y] - местоположение радиомаяка, а координатами [x_i,y_i],  i = 1,N ¯ - множество из N позиций на траектории перемещения запросчика, в которых измеряется дальность до радиомаяка. Аддитивные ошибки измерения дальностей будем считать независимыми нормальными случайными величинами с нулевым математическим ожиданием и одинаковыми дисперсиями σ R 2 . Тогда функция правдоподобия для независимых измерений представляет собой произведение условных гауссовских функций плотности вероятности:

где R ˜ i ,  i = 1,N ¯ - вектор измеренных расстояний.

Нетрудно заметить, что функция правдоподобия (1) достигает наибольшего значения при минимальной величине аргумента экспоненты. Следовательно, оценкой координат радиомаяка по результатам дальномерных измерений являются аргументы минимизации функции правдоподобия (1):

где F ( x ,  y ) = ∑ i = 1 N ( ( x i − x ) 2 + ( y i − y ) 2 − R ˜ i ) 2 .                                             ( 3 )

Определим на основании полученной функции правдоподобия (1) потенциальную точность оценки местоположения источника радиоизлучения дальномерным методом. Для этого воспользуемся выражением логарифма этой функции правдоподобия, применяя которое можно построить эталонную ковариационную матрицу, являющейся нижней границей дисперсии оценки координат [x,y]. Такая граница определяется неравенством Рао-Крамера [4, с.533…538]:

C O V ( x ,  y ) ≥ Ф − 1 = [ D x K x y K x y D y ] ,                                                            (4)

где D_x - дисперсия оценки по оси X; K_xy - корреляционный момент оценки координат; D_y - дисперсия оценки по оси Y;

Ф - информационная матрица Фишера; E[•] - символ математического ожидания. Найдем значения частных производных в (5).

С этой целью представим логарифм функции правдоподобия (1) в следующем виде

где S i [ x ,   y ] = ( x i − x ) 2 + ( y i − y ) 2 .                                                                          (7)

Вычисление в общем виде производных в (5) с учетом (6) и (7) дает следующие результаты:

Так как по условию постановки задачи случайная величина ( S i [ x ,  y ] − R ˜ i ) распределена по нормальному закону с нулевым математическим ожиданием, то

E [ ∑ i = 1 N { ( S i [ x ,  y ] − R ˜ i ) ⋅ ∂ 2 S i [ x ,  y ] ∂ x 2 } ] = = E [ ∑ i = 1 N { ( S i [ x ,  y ] − R ˜ i ) ⋅ ∂ 2 S i [ x ,  y ] ∂ y 2 } ] = E [ ∑ i = 1 N { ( S i [ x ,  y ] − R ˜ i ) ⋅ ∂ 2 S i [ x ,  y ] ∂ x ∂ y } ] = 0   .             (9)

Тогда на основании (6)-(9) и с учетом того, что математическое ожидание функции, не имеющей случайных параметров, равно значению этой функции, получаем общие формулы для вычисления матрицы Фишера:

где

{ ∂ S i [ x ,  y ] ∂ x = x − x i ( x i − x ) 2 + ( y i − y ) 2 ; ∂ S i [ x ,  y ] ∂ y = y − y i ( x i − x ) 2 + ( y i − y ) 2 .                                      (11)

Таким образом, матрица Фишера приобретает окончательный вид:

Ф = [ 1 σ R 2 ∑ i = 1 N ( ∂ S i [ x ,  y ] ∂ x ) 2           1 σ R 2 ∑ i = 1 N ∂ S i [ x ,  y ] ∂ x ⋅ ∂ S i [ x ,  y ] ∂ y 1 σ R 2 ∑ i = 1 N ∂ S i [ x ,  y ] ∂ y ⋅ ∂ S i [ x ,  y ] ∂ x       1 σ R 2 ∑ i = 1 N ( ∂ S i [ x ,  y ] ∂ y ) 2    ] = − 1 σ R 2 ⋅ [ A − B − B C ] ,              (12)

где

A = ∑ i = 1 N ( x − x i ) 2 ( x i − x ) 2 + ( y i − y ) 2 ;                                        (13)

B = ∑ i = 1 N ( y − y i ) ⋅ ( y − y i ) ( x i − x ) 2 + ( y i − y ) 2 ;                                        (14)

C = ∑ i = 1 N ( y − y i ) 2 ( x i − x ) 2 + ( y i − y ) 2 ;                                        (15)

Полученное выражение (12) для расчета матрицы Фишера свидетельствуют о том, что ковариационная матрица оценки координат [x,y], определяемая неравенством Рао-Крамера (4), не содержит в себе вектор измерения дальностей R ˜ i ,  i = 1,N ¯ , не зависит от алгоритма поиска аргументов минимизации функции правдоподобия и определяется только конкретной совокупностью координат точек измерения дальностей [x_i,y_i],  i = 1,N ¯ задающей вид траектории перемещения запросчика.

Поскольку расчетные оценки координат радиомаяка [x^*,y^∗], получаемые методом максимального правдоподобия в рамках сделанных выше допущений, асимптотически нормальны с математическим ожиданием [x,y] и ковариационной матрицей Ф^-1 [4, с.546…547], то функция плотности вероятности [x^*,y^∗] может быть описана двумерным гауссовским распределением [5, с.231]:

W [ x * , y ∗ ] = 1 2 π ⋅ σ x ⋅ σ y 1 − r x y 2 exp ⋅ ⋅ { − 1 2 1 − r x y 2 [ ( x * − x ) 2 σ x 2 + 2 ⋅ r x y ⋅ ( x * − x ) ⋅ ( y * − y ) σ x ⋅ σ y + ( y * − y ) 2 σ y 2 ] } ,             (16)

где σ x 2 , σ y 2 , r_xy - определяются из ковариационной матрицы (5): σ x 2 = D x ; σ y 2 = D y ; r x y = K x y / D x ⋅ D y .

В геометрической интерпретации совместная двумерная плотность вероятности (16) представляет собой холмообразную поверхность, вершина которой находится над точкой [x,y] плоскости x0y. Сечение поверхности W[x^*,y^*] плоскостью, параллельной x0y, представляет собой эллипс рассеяния [5, с.235], уравнение проекции которого на плоскость x0y имеет вид:

[ ( x * − x ) 2 σ x 2 + 2 ⋅ r x y ⋅ ( x * − x ) ⋅ ( y * − y ) σ x ⋅ σ y + ( y * − y ) 2 σ y 2 ] = p e 2 .                        (17)

где p_e - параметр, определяющий вероятность попадания расчетной оценки координат в эллипс рассеяния (например, вероятность попадания в эллипс рассеяния с параметром p_e - 1,73 равна 0.95 [6, c.26]).

Размеры большой (a) и малой (b) полуосей эллипса рассеяния, а также угол (β) его ориентации (угол между большой осью эллипса и положительным направлением оси 0x, отсчитываемый против часовой стрелки) рассчитываются по формулам [7, с.580]:

a ( b ) = 2 ⋅ σ R ⋅ p e / A + C − ( + ) ( A − C ) 2 + 4 B 2 ,                              (18)

β = a r c t g [ 2 B / ( C − A ) ] / 2 ,    - π /2 < β ≤ π /2                                             (19)

Приведенные выше выражения позволяют очертить границы возможного расхождения расчетных оценок относительно истинных значений координат радиомаяка.

Без потери общности рассуждений радиомаяк можно поместить в начало системы координат: x=0, y=0, а i-ю позицию измерения дальности представить относительно местоположения радиомаяка в полярных координатах [R_i, α_i],  i = 1,N ¯ , где как показано на фиг.1а: α_i - угол между направлением от радиомаяка на i-ю позицию измерителя и осью 0x: α_i=arctg[y_i/x_i]; R_i - истинное расстояние от радиомаяка до i-й позиции измерения дальности. Тогда в предположении малых некоррелированных ошибок измерений дальностей (R_i>>σ_R,  i = 1,N ¯ ) вектор измеренных расстояний R ˜ i ,  i = 1,N ¯ будет нормально распределенным, а выражения для расчета элементов матрицы Фишера (13)-(15) значительно упростятся:

A = ∑ i = 1 N ( x − x i ) 2 ( x i − x ) 2 + ( y i − y ) 2 = ∑ i = 1 N ( R i ⋅ cos [ α i ] ) 2 ( R i ⋅ cos [ α i ] ) 2 + ( R i ⋅ sin [ α i ] ) 2 = ∑ i = 1 N ( cos [ α i ] ) 2 ;        (20)

B = − ∑ i = 1 N ( y − y i ) ⋅ ( x − x i ) ( x i − x ) 2 + ( y i − y ) 2 = − ∑ i = 1 N ( R i ⋅ sin [ α i ] ) × ( R i ⋅ cos [ α i ] ) ( R i ⋅ cos [ α i ] ) 2 + ( R i ⋅ sin [ α i ] ) 2 = − ∑ i = 1 N sin [ α i ] × cos   [ α i ] ;     (21)

C = ∑ i = 1 N ( y − y i ) 2 ( x i − x ) 2 + ( y i − y ) 2 = ∑ i = 1 N ( R i ⋅ sin [ α i ] ) 2 ( R i ⋅ cos [ α i ] ) 2 + ( R i ⋅ sin [ α i ] ) 2 = ∑ i = 1 N ( R i ⋅ sin [ α i ] ) 2 .     (22)

Так как по условиям постановки задачи радиомаяк неподвижен, позиции измерения на траектории движения запросчика могут быть перенумерованы произвольно, например, так, чтобы угол между направлением от радиомаяка на i-ю позицию запросчика α_i всегда увеличивался (фиг.1б).

Следовательно, с учетом (20)-(22) можно утверждать, что в рамках принятых ограничений и допущений (R_i>>σ_R,  i = 1,N ¯ ) любая траектория перемещения запросчика относительно радиомаяка может быть однозначно задана только возрастающей последовательностью углов α_i и углом визирования базы измерений¹ Θ (¹ Угол визирования базы измерений задается между направлениями от радиомаяка на крайние точки траектории движения эапросчика (на фиг.1б - это угол между направлениями наточку «1» и «8»)). В связи с этим задача обоснования траектории перемещения запросчика, обеспечивающей при фиксированном количестве позиций измерения - дальности минимальную ошибку оценки координат радиомаяка, сводится фактически к задаче обоснования угла визирования базы измерений, минимизирующего площадь эллипса ошибок: S=π·a·b.

Пусть угол между направлением от радиомаяка на i-ю позицию запросчика и осью 0x возрастает по линейному закону: α i = i × Θ N . Тогда суммы в (20)-(22) могут быть представлены в замкнутой форме [7]:

A = ∑ i = 1 N ( cos [ α i ] ) 2 = N 2 + 1 2 ⋅ sin [ Θ ] ⋅ cos [ ( N + 1 ) ⋅ Θ N ] / sin [ Θ N ] ;        (23)

B = − ∑ i = 1 N sin [ α i ] × cos [ α i ] = − 1 2 ⋅ sin [ Θ ] ⋅ sin [ ( N + 1 ) ⋅ Θ N ] / sin [ Θ N ] ;        (24)

C = ∑ i = 1 N ( sin [ α i ] ) 2 = N 2 − 1 2 ⋅ sin [ Θ ] ⋅ cos [ ( N + 1 ) ⋅ Θ N ] / sin [ Θ N ] .                 (25)

С учетом (23)-(25) выражения (18) для расчета большой и малой полуосей эллипса ошибок приобретают вид:

a ( b ) = 2 ⋅ σ R / A + C − ( + ) ( A − C ) 2 + 4 B 2 = 2 ⋅ σ R / N − ( + ) ( sin [ Θ ] / sin [ Θ N ] ) 2 ,    (26)

а площадь эллипса ошибок вычисляется по формуле:

S = π ⋅ a ⋅ b = 2 ⋅ π ⋅ σ R 2 ⋅ p e 2 N 2 − ( sin [ Θ ] / sin Θ N ) 2 .                        (27)

Очевидно, что площадь эллипса ошибок будет минимальной при максимальном значении знаменателя в (27). Это достигается для sin [ Θ ] / sin Θ N = 0 , то есть когда:

Θ = k ⋅ π ,                                           (28)

где k - целое число, k=1, 2, 3….

Проиллюстрируем справедливость (28) следующим примером. Пусть вероятность попадания расчетной оценки координат радиомаяка в эллипс рассеяния задана равной 0.95, что соответствует параметру p_e=1.73 в выражении (17), а траектория движения запросчика представляет собой дугу с центром в точке нахождения ИРИ [x,y] и неизменным радиусом R.

В общем виде оценка координат радиомаяка как аргумент минимизации функции правдоподобия (1) может быть вычислена через определение глобального экстремума целевой функции (3) F(x,y) путем решения системы уравнений:

{ ∂ F ( x ,   y ) ∂ x = 0 , ∂ F ( x ,   y ) ∂ y = 0.                                            (29)

Вследствие нелинейности целевой функции (3), характерный вид которой иллюстрируется на фиг.2, поиск корней уравнений (29) может производиться численными методами на ЭВМ (например, с использованием функций пакета Matlab).

Результаты решения уравнений (29), полученные для некоторых частных случаев с использованием имитационного моделирования средствами Matlab R2012a, приведены на фиг.3-5.

Здесь радиомаяк располагается в центре осей координат[x=0, y=0], а результаты абсолютного большинства численных оценок координат радиомаяка группируются в виде точек