Способ определения природных напряжений в массиве горных пород

Способ определения природных напряжений в массиве горных пород

Иллюстрации

Показать все

Реферат

Изобретение относится к способам определения природных напряжений в массиве горных пород, которые используются в качестве граничных условий при расчете напряжений в горных конструкциях и элементах систем разработки для оценки их устойчивости.

Известен способ определения природных напряжений, основанный на гипотезах их формирования только под действием гравитационных сил [1]. По гипотезе А. Гейма природные напряжения не превышают силы тяжести столба налегающих пород:

σ x = σ y = σ z = − γ H ,                                                 (1)

где σ_z - вертикальная составляющая, МПа;

σ_x, σ_y -горизонтальные составляющие, МПа;

γ - удельный вес налегающих пород, МН/м³;

H - мощность налегающих пород, м.

По гипотезе А.Н. Динника горизонтальные составляющие зависят от бокового распора вертикальных напряжений λ

σ x = σ y = − λ γ H ,                                                      (2)

где λ = μ 1 − μ ,

µ - коэффициент Пуассона.

Недостатком известных способов является то, что они не учитывают воздействие тектонических сил, которые участвуют в формировании горизонтальных природных напряжений.

Наиболее близким к предлагаемому способу по технической сущности и достигаемому результату являются разнообразные способы непосредственного измерения напряжений в исследуемых массивах горных пород, основанные на частичной и полной разгрузке массива и его гидроразрыве [1].

В результате экспериментальных работ получаем

σ z = λ γ H ,                                                                  (3)

σ x = λ γ H + σ т х ,                                                         (4)

σ x = λ γ H + σ т у ,                                                         (5)

где σ_тх, σ_ту - тектонические напряжения, действующие по осям X и Y.

Недостатком известных способов является то, что тектонические силы включают постоянную (не зависит от времени измерения) и переменную составляющие, которая периодически изменяется во времени с цикличностью 3,5 года, 11 лет, 90 лет и т.п.

Однако все известные способы при производстве измерений и обработке результатов не позволяют разделять эти составляющие и полученный результат характеризует напряженное состояние массива только в момент измерения и при использовании этих данных через 5, 10 и 11 лет ошибки при расчете устойчивости горных конструкций могут достигать значительной величины.

Целью изобретения является повышение точности прогнозирования напряжений на нижние горизонты в будущем времени и при использовании результатов измерений в прошедшем времени на верхних горизонтах.

Указанная цель достигается тем, что определенные известными способами главные напряжения разделяют на постоянную и переменную (пульсирующую) во времени составляющие

σ x = ( λ γ H + σ х т ) + σ х т п ,                                                  (6)

σ у = ( λ γ H + σ у т ) + σ у т п ,                                                  (7)

так как σ_хтп≈σ_утп=σ_тп, получают зависимость изменения постоянных составляющих с глубиной, находят закономерность изменения переменных (пульсирующих) напряжений во времени на рассматриваемом месторождении или принимают их как средние по региону, а затем суммируют эти составляющие на требуемой глубине и в нужное время.

Ситуация облегчается тем, что σ_тп присущи всей земной коре и величина их одинакова как на Урале, так и для всего земного шара [2]. Деформация земной коры и связанные с ней σ_тп на Урале и на вулканических островах Тихого, Индийского и Атлантического океанов в экваториальной зоне, на которых находятся станции коррекции спутников GPS, отличаются не более чем на 5%.

В качестве примера рассмотрим условия определения и прогнозирования природных напряжений на Гайском подземном руднике, где природные напряжения измеряли методом щелевой разгрузки, σ_тп определяли на специальном полигоне в околоствольном дворе на гор. 830 м.

Гор., м	Год	Измеренные	Постоянные σп=σiσтп
σz	σx	σy	σтп	σ x П	σy
830	1998	-22	-40	-19	-7	-33	-12
910	2004	-25	-42	-20	-4	-38	-16
1070	2008	-33	-49	-32	-9	-40	-23

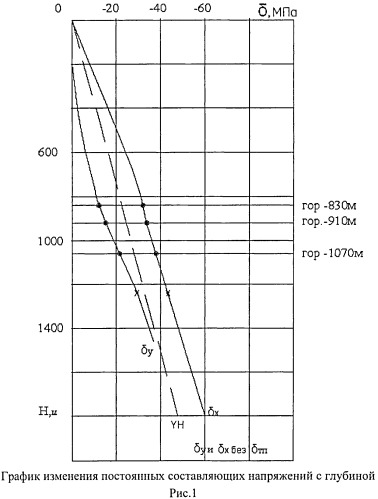
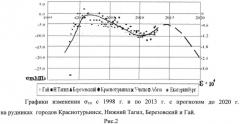
На рис.1 представлены графики изменения постоянных составляющих напряжений с глубиной, а на рис.2 - графики изменения σ_тп с 1998 г. и по 2013 г. с прогнозом до 2020 г. на рудниках городов Краснотурьинск, Нижний Тагил, Березовский и Гай.

Источники информации

1. Ральникова М.В., Зотеев О.В. Геомеханика: Учебное пособие. - М.: Издательский дом «Руда и Металлы, 2003. - 240 с.

2. Зубков А.В. Периодическое расширение и сжатие Земли как вероятный механизм природных катаклизмов. - Литосфера, 2013. №2, с.145-156.

1. Способ определения природных напряжений в массиве горных пород, включающий измерение напряжений в массиве горных пород известными методами за пределами зоны влияния очистных (горных) работ на различной глубине при использовании подземных выработок, построение графиков (зависимостей) изменения полученных главных напряжений с глубиной, отличающийся тем, что для повышения точности прогнозирования напряжений, в том числе и на глубине горизонта, каждое из главных напряжений разделяют на постоянную и переменную (пульсирующие) во времени составляющие, получают зависимость изменения постоянных составляющих с глубиной, находят закономерность изменения переменных (пульсирующих) напряжений σ_тп во времени, а затем суммируют эти составляющие на требуемой глубине и в нужное время.

2. Способ по п.1, отличающийся тем, что график изменения σ_тп во времени принимают как среднее значение по региону.