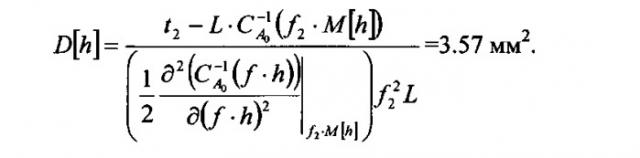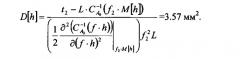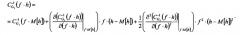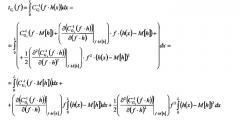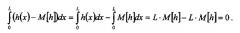Способ контроля за динамикой изменения толщины стенки контролируемого объекта

Способ контроля за динамикой изменения толщины стенки контролируемого объекта

Иллюстрации

Показать все

Реферат

Заявленное изобретение относится к области технической диагностики и неразрушающего контроля промышленных объектов и используется для контроля за динамикой изменения минимального значения толщины стенки тонкостенных и листовых изделий, а также других изделий, в которых могут распространяться волны Лэмба, например трубопроводов, резервуаров, сосудов, цистерн.

Уровень техники.

Известен способ измерения толщины изделия (патент РФ №2231753, опубл. 27.06.2004) с помощью ультразвуковых импульсов, заключающийся в том, что с помощью ультразвукового преобразователя излучают в материал изделия ультразвуковой импульс, принимают из него эхо-импульсы, отраженные от противоположных поверхностей материала, измеряют время распространения эхо-импульсов от одной поверхности до другой и обратно и вычисляют толщину как произведение половины этого времени на известную скорость распространения ультразвуковых импульсов в материале.

Необходимость обеспечения физического доступа к поверхности всех контролируемых участков изделия и высокая трудоемкость контроля больших по площади изделий снижают эффективность известного способа.

Известен способ (патент WO 2007139389, опубл. 06.12.2007) измерения величины потери средней толщины материала твердой структуры, способной поддерживать распространение акустических волн и во время работы контактирующей с одним или несколькими веществами, приводящими к изменению толщины структуры, заключающийся в использовании множества датчиков любого типа, установленных в контакте с поверхностью указанной твердой структуры, и отличающийся тем, что включен один или несколько из следующих шагов:

а) выполнение один или большее число раз этапа передачи акустического сигнала по крайней мере от одного из множества акустических датчиков в стенку указанной структуры и прием переданного акустического сигнала множеством указанных датчиков после прохождения дистанции в твердой структуре;

б) сбор сигналов с указанного множества датчиков в блок обработки;

в) анализ и сравнение принятых сигналов, сгенерированных на шаге (а), и/или результатов, соответствующих более ранним измерениям;

г) вычисление степени потери толщины материала указанной твердой структуры по результатам анализа, выполненного на шаге (в),

причем блок обработки данных способен вычислять среднее снижение истинной толщины стенки в пределах области твердой структуры путем анализа сигналов, принятых преобразователями.

Недостатком известного способа является необходимость измерения средней толщины при установке датчиков на объект для последующего получения текущих значений средней толщины, что значительно снижает эффективность известного способа.

Известен способ (патент US 5965818, опубл. 12.10.1999) измерения минимального значения толщины стенки трубы, лежащей на опоре, при помощи ультразвуковых волн Лэмба, включающий

а) установку передающего преобразователя и приемного преобразователя на указанной трубе на противоположных сторонах от опоры указанной трубы;

б) излучение в указанную трубу указанным передающим преобразователем высокодисперсной и монотонной части волны Лэмба S₀, у которой значения произведения частоты на толщину равны или меньше значения, соответствующего минимуму групповой скорости;

в) прием указанных волн Лэмба указанным приемным преобразователем;

г) измерение времени, требуемого для того, чтобы указанная излученная волна Лэмба была принята указанным приемным преобразователем, указанное время далее называется время пролета;

д) повтор шагов от а) до г) для получения реперного значения времени пролета без изменения настроек прибора, но с перемещением указанных преобразователей в точки, расположенные рядом с указанной опорой трубы;

е) определение изменения величины времени пролета, вызванного локальными коррозионными потерями в стенке, путем вычитания времени пролета, измеренного на опоре трубы, из реперного значения времени пролета и

ж) определение толщины трубы на указанной опоре трубы с использованием указанного изменения величины времени пролета.

Недостатком известного способа является невозможность определения минимального значения толщины стенки за пределами области соприкосновения трубы и опоры, что значительно снижает эффективность способа.

Наиболее близким по технической сущности является способ (патент US 6360609, опубл. 26.03.2002) измерения толщины в многомодовых дисперсионных условиях, заключающийся в том, что излучают в первой точке в среду многомодовую обладающую дисперсией акустическую нормальную волну, принимают во второй точке многомодовую обладающую дисперсией акустическую нормальную волну, с использованием частотно-временного анализа проводят частотное разложение многомодовой обладающей дисперсией акустической нормальной волны, выбирают частоту, которая определяет групповую задержку t_g нормальной волны на каждой имеющейся на этой частоте моде, выбирают моду и определяют групповые задержки по сравнению с первой точкой, определяют расстояние L между первой и второй точкой, выбирают моду и определяют групповую задержку t_g по сравнению с первой точкой, вычисляют групповую скорость c_g=L/t_g, определяют толщину по дисперсионному соотношению.

Недостатком известного способа является условие постоянства на всем пути между первой и второй точкой величины групповой скорости выбранной моды на выбранной частоте, которое не выполняется при наличии вариаций значений толщины между первой и второй точкой, к примеру при наличии на объекте очаговой коррозии.

Раскрытие изобретения.

Технический результат, достигаемый от реализации заявленного решения, заключается в снижении трудоемкости, упрощении и ускорении контроля толщины стенки больших по площади объектов, устранении необходимости получения физического доступа ко всей поверхности объекта, подлежащей контролю толщины, обеспечении возможности контроля толщины при наличии вариаций значений толщины, к примеру при наличии на объекте очаговой коррозии, обеспечении возможности определения среднеарифметического и минимального значений толщины на участке между двумя акустическими преобразователями, установленными на объекте в произвольных точках, без проведения предварительного измерения толщины в тех же точках.

Сущность способа заключается в том, что размещают на его поверхности на известном расстоянии друг от друга, по крайней мере, один акустический преобразователь для излучения волн Лэмба и, по крайней мере, один преобразователь для их приема, излучают в заданный момент времени импульсный сигнал, производят расчет зависимости спектральной плотности мощности принятого сигнала от времени, выбирают волны Лэмба и частоты, определяют разность между временем приема выбранной частотной составляющей выбранной волны Лэмба и временем излучения сигнала, определяют значения групповой скорости выбранной частотной составляющей выбранной волны Лэмба по известному значению расстояния между преобразователями и значению разности между временем приема выбранной частотной составляющей выбранной волны Лэмба и временем излучения сигнала, определяют значения толщины стенки по полученному значению групповой скорости, выбранному значению частоты и эталонной зависимости групповой скорости выбранной волны Лэмба от произведения толщины стенки и частоты, при этом устанавливают минимальную величину толщины стенки по полученным среднеарифметической величине толщины стенки и дисперсии значений толщины стенки объекта, причем среднеарифметическое значение толщины стенки определяют с выбором симметричной волны Лэмба нулевого порядка и, по крайней мере, одной частоты, на которой эталонная зависимость обратной величины групповой скорости симметричной волны Лэмба нулевого порядка от произведения толщины стенки и частоты близка к линейной, а дисперсию значений толщины стенки определяют с выбором антисимметричной волны Лэмба нулевого порядка и частоты, на которой эталонная зависимость обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка от произведения толщины стенки и частоты существенно нелинейна.

Краткое описание чертежей.

На фиг.1 приведены графики зависимостей групповых скоростей симметричной волны Лэмба нулевого порядка S₀ и антисимметричной волны Лэмба нулевого порядка A₀ от произведения частоты f и толщины h стенки объекта. На фиг.2 приведен пример принятого акустического сигнала. На фиг.3 приведен пример зависимости спектральной плотности мощности принятого сигнала от времени. На фиг.4 приведены пример выявления прихода симметричной волны Лэмба нулевого порядка S₀ и антисимметричной волны Лэмба нулевого порядка A₀ на графике зависимости спектральной плотности мощности сигнала от времени, пример двух частотных диапазонов, в пределах которых зависимость обратной величины групповой скорости симметричной волны Лэмба нулевого порядка S₀ от частоты близка по форме к линейной зависимости, и пример частотного диапазона, в пределах которого зависимость обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ от частоты существенно нелинейна. Также на фиг.4 приведены примеры определения времен приема выбранных волн Лэмба на частотах, принадлежащих указанным участкам. На фиг.5 приведен пример графика значений производной второго порядка обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка по произведению частоты f и толщины h стенки. На фиг.6 приведен пример нахождения значения произведения толщины стенки и частоты, при котором эталонное значение групповой скорости симметричной волны Лэмба нулевого порядка S₀ равняется полученному путем анализа принятого сигнала значению групповой скорости.

Осуществление изобретения.

Способ осуществляют следующим образом.

Размещают на поверхности стенки объекта, например трубопровода, на известном расстоянии L друг от друга, по крайней мере, один акустический преобразователь для излучения волн Лэмба и, по крайней мере, один преобразователь для их приема.

Излучатель испускает в заданный момент времени импульсный акустический сигнал.

Принимают сигнал приемником волн Лэмба.

Выполняют расчет зависимости спектральной плотности мощности принятого сигнала от времени.

Определяют минимальное значение толщины стенки объекта h_min на участке между преобразователями. Для этого определяют среднеарифметическое значение M[h] толщины стенки объекта на участке между преобразователями и дисперсию значений D[h] толщины стенки объекта на участке между преобразователями. Для этого определяют среднеарифметическое значение M[h] толщины стенки объекта на участке между преобразователями. Для этого выбирают первое значение частоты f₁ такое, что в его окрестности эталонная зависимость обратной величины групповой скорости симметричной волны Лэмба нулевого порядка S₀ от произведения толщины стенки и частоты близка к линейной зависимости.

Определяют первую разницу времен t₁ между временем приема частотной составляющей симметричной волны Лэмба нулевого порядка S₀ на первой выбранной частоте f₁ и временем излучения по зависимости спектральной плотности мощности принятого сигнала от времени.

По значению первой разницы времен t₁ и по значению расстояния L между преобразователями определяют значение групповой скорости С_ГР выбранной частотной составляющей симметричной волны Лэмба нулевого порядка S₀ по формуле

С Г Р = L t 1 .

По известным формулам рассчитывают эталонные зависимости от произведения частоты f и толщины h значений групповой скорости C S 0 ( f ⋅ h ) симметричной волны Лэмба нулевого порядка S₀, значений групповой скорости C A 0 ( f ⋅ h ) антисимметричной волны Лэмба нулевого порядка A₀ и значений второй производной ∂ 2 ( C A 0 − 1 ( f ⋅ h ) ) ∂ ( f ⋅ h ) 2 обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ по произведению частоты и толщины.

Подбирают значение толщины M[h], при котором значение эталонной групповой скорости симметричной волны Лэмба нулевого порядка S₀ на первой выбранной частоте f₁ равняется полученному путем анализа принятого сигнала значению групповой скорости

C S 0 ( f 1 ⋅ M [ h ] ) = C Г Р .

Полученное значение толщины M[h] считают среднеарифметическим значением толщины стенки на участке между преобразователями.

Затем определяют дисперсию значений D[h] толщины стенки объекта на участке между преобразователями. Для этого выбирают второе значение частоты f₂ такое, что в его окрестности эталонная зависимость обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ от произведения толщины стенки и частоты существенно нелинейна.

Определяют вторую разницу времен t₂ между временем приема частотной составляющей антисимметричной волны Лэмба нулевого порядка A₀ на второй выбранной частоте f₂ и временем излучения по зависимости спектральной плотности мощности принятого сигнала от времени.

Определяют дисперсию D[h] значений толщины стенки объекта по значениям второй выбранной частоты f₂, второй разницы времен t₂, расстояния L между преобразователями, среднеарифметическому значению толщины M[h], эталонным значениям групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ и второй производной ее обратной величины по произведению частоты и толщины, к примеру, по формуле

Определяют минимальное значение толщины стенки объекта h_min по среднеарифметическому значению толщины M[h] и дисперсии значений толщины D[h], к примеру, по формуле

Пример конкретного выполнения способа.

Предлагаемый способ испытан на стальной пластине длиной L=1 м. На 50% длины пластины ее толщина равнялась 10 мм, на других 50% длины пластины ее толщина в результате воздействия коррозии была уменьшена до 8 мм. Таким образом, минимальное значение толщины составляло 8 мм, среднеарифметическое значение толщины равнялось 9 мм.

В качестве акустических преобразователей для излучения и приема волн Лэмба использовались пьезоакустические преобразователи акустической эмиссии. Их установили на дальних краях пластины. Для излучения сигнала подали в заданный момент времени на электрический вход излучающего преобразователя импульсный электрический сигнал. Излучатель испустил импульсный акустический сигнал. Сигнал распространился по пластине в виде комбинации симметричной и антисимметричной волн Лэмба нулевого порядка S₀ и A₀, обладающих зависимостью групповой скорости от частоты и толщины стенки (фиг.1). Приемник принял сигнал U(t) (фиг.2). Из осциллограммы принятого сигнала U(t) путем преобразования Чои-Вильямса была получена зависимость спектральной плотности мощности принятого сигнала от времени W(f, t) (фиг.3).

Определили первой значение частоты f₁, в окрестности которой эталонная зависимость обратной величины групповой скорости симметричной волны Лэмба нулевого порядка S₀ от произведения частоты и толщины близка к линейной зависимости. Для этого воспользовались тем фактом, что у объектов из стали подходящими являются значения первой частоты f₁ из диапазона от 1.7 МГц·мм/М[h] до 2.4 МГц·мм/М[h] или из диапазона от 2.7 МГц·мм/М[h] до 3.4 МГц·мм/М[h], где M[h] - среднеарифметическое значение толщины (фиг.4). Исходя из начального значения толщины (10 мм) стенки, выбрали значение первой частоты f₁, равное f₁=230 кГц (фиг.4).

По зависимости спектральной плотности мощности принятого сигнала от времени W(f, t) определили первую разницу времен t₁ между временем приема симметричной волны Лэмба нулевого порядка S₀ на первой выбранной частоте f₁ и временем излучения.

Для этого провели определение времени приема следующим способом: выбрали уровень порога, равный 1% от максимального абсолютного значения зависимости спектральной плотности мощности принятого сигнала от времени, выявили на зависимости спектральной плотности мощности сигнала от времени W(f, t) точки, абсолютная величина спектральной плотности в которых превышает порог. Множество выявленных точек образовало на зависимости спектральной плотности 2 кривые характерной формы, соответствующие временам приема различных частотных составляющих симметричной S₀ и антисимметричной A₀ волн Лэмба нулевого порядка. Выявили точки, соответствующие симметричной волне Лэмба нулевого порядка S₀ и первой выбранной частоте f₁, выбрали из них точку, имеющую наибольшее соответствующее ей абсолютное значение спектральной плотности мощности принятого сигнала от времени. Соответствующее данной точке значение времени использовали в качестве времени приема симметричной волны Лэмба нулевого порядка S₀ на первой выбранной частоте f₁. В качестве времени излучения использовали время подачи управляющего электрического импульса на излучающий пьезоакустический преобразователь акустической эмиссии.

Определенная указанным способом первая разница времен t₁ оказалась равной t₁=404.9 мкс.

По значению первой разницы времен t₁ и по значению расстояния L между преобразователями определили значение групповой скорости С_ГР выбранной частотной составляющей симметричной волны Лэмба нулевого порядка S₀ по формуле

По известным формулам рассчитали эталонные зависимости от произведения частоты f и толщины h значений групповой скорости C S 0 ( f ⋅ h ) симметричной волны Лэмба нулевого порядка S₀, значений групповой скорости C A 0 ( f ⋅ h ) антисимметричной волны Лэмба нулевого порядка A₀ (фиг.1) и значений второй производной ∂ 2 ( C A 0 − 1 ( f ⋅ h ) ) ∂ ( f ⋅ h ) 2 обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ по произведению частоты и толщины (фиг.5).

Подобрали значение толщины M[h], при котором эталонное значение групповой скорости C S 0 симметричной волны Лэмба нулевого порядка S₀ на первой выбранной частоте f₁ равняется полученному по значению первой разницы времен t₁ значению групповой скорости С_ГР

C S 0 ( f 1 ⋅ M [ h ] ) = C Г Р = 2470 м / с .

Для этого сначала по эталонной зависимости групповой скорости симметричной волны Лэмба нулевого порядка S₀ от произведения частоты и толщины определили значение произведения толщины на частоту f₁·M[h], при котором выполняется искомое равенство (фиг.6)

f₁·М[h]=2124.5 кГц·мм,

затем определили само значение толщины M[h]

M[h]=2124.5 кГц·м/f₁=9.24 мм.

Полученное значение M[h] стали считать среднеарифметическим значением толщины стенки участка объекта между преобразователями.

Определили значение второй частоты f₂, в окрестности которой эталонная зависимость обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ от произведения частоты и толщины существенно нелинейна. Для этого воспользовались тем фактом, что у объектов из стали подходящими являются значения второй частоты f₂ из диапазона от 0 МГц·мм/М[h] до 1.0 МГц·мм/М[h] (фиг.4). Исходя из начального значения толщины (10 мм) стенки, выбрали значение второй частоты, равное f₂=25 кГц (фиг.4).

По зависимости спектральной плотности мощности принятого сигнала от времени W(f, t) определили вторую разницу времен t₂ между временем приема антисимметричной волны Лэмба нулевого порядка A₀ на второй выбранной частоте f₂ и временем излучения t₂=424.4 мкс (фиг.4).

Взяли значение второй производной ∂ 2 ( C A 0 − 1 ( f ⋅ h ) ) ∂ ( f ⋅ h ) 2 обратной величины групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ по произведению частоты и толщины при значении произведения частоты на толщину, равном произведению второй выбранной частоты на среднеарифметическое значение толщины f₂·M[h]=230.9 кГц·мм (фиг.5)

Определили дисперсию D[h] значений толщины стенки объекта по значениям второй выбранной частоты f₂, второй разницы времен t₂, расстояния L между преобразователями, среднеарифметическому значению толщины M[h], эталонным значениям групповой скорости антисимметричной волны Лэмба нулевого порядка A₀ и второй производной ее обратной величины по произведению частоты и толщины по формуле

Определили минимальное значение толщины стенки h_min объекта на участке между преобразователями по среднеарифметическому значению толщины M[h] на участке между преобразователями и дисперсии значений толщины D[h] на участке между преобразователями по формуле

Таким образом, предлагаемый способ является высокоэффективным и может при широком внедрении принести значительный экономический эффект за счет

снижения трудоемкости, упрощения и ускорения контроля толщины больших по площади объектов,

устранения необходимости получения физического доступа ко всей поверхности объекта, подлежащей контролю толщины,

обеспечения возможности контроля толщины при наличии вариаций значений толщины, к примеру при наличии на объекте очаговой коррозии,

обеспечения возможности определения среднеарифметического и минимального значений толщины на участке между двумя акустическими преобразователями, установленными на объекте в произвольных точках, без проведения предварительного измерения толщины в тех же точках.

Математический расчет.

Теоретические исследования и анализ литературных источников показали, что в стенке объекта акустический сигнал на частотах, на которых длины объемных волн сравнимы или превосходят толщину стенки, распространяется в виде волн Лэмба. Значение групповой скорости С_ГР волны Лэмба зависит (фиг.1) от произведения частоты f и толщины стенки объекта h, а также от значений скоростей объемной продольной C_L и объемной поперечной C_T волн в материале стенки, типа G волны Лэмба (симметричная S или антисимметричная A) и порядкового номера i волны Лэмба

С Г Р = C G i ( f ⋅ h , C L , C T ) .

Значение групповой скорости С Г Р = C G i ( f ⋅ h , C L , C T ) можно рассчитать по известной формуле для произвольных значений частоты f, толщины стенки h и для любого материала, взяв значения скоростей объемной продольной C_L и объемной поперечной C_T волн из справочника (к примеру, для стали они равны 5900 м/с и 3260 м/с соответственно). Значения скоростей объемной продольной C_L и объемной поперечной C_T волн далее считаются известными и постоянными и для краткости опущены.

Известно, что излучение акустического импульса эквивалентно синхронному излучению множества частотных составляющих. В этом случае различные частотные составляющие различных волн Лэмба приходят (фиг.2) на приемный преобразователь в различные моменты времени t G i ( f ) , определяемые уравнением

где f - частота, x - координата вдоль прямой линии, соединяющей преобразователи, начало координат соответствует точке, в которой установлен излучающий преобразователь, h(x) - зависимость толщины стенки объекта от координаты x, L - расстояние между преобразователями, время t G i ( f ) отсчитывается от времени излучения импульса, G - тип волны Лэмба, i - порядковый номер волны Лэмба.

Расчет зависимости спектральной плотности мощности принятого сигнала от времени (фиг.3) позволяет определить время приема t G i ( f ) каждой частотной составляющей каждой волны Лэмба (фиг.4).

Разложение функции C G i − 1 ( f ⋅ h ) в ряд Тейлора до членов второго порядка в окрестности величины f·M[h], где величина M[h] равна среднеарифметическому значению толщины стенки M [ h ] = 1 L ∫ 0 L h ( x ) d x , выглядит следующим образом:

Следовательно, время приема равно

Поскольку , то

Следовательно,

где величина

является дисперсией значений толщины стенки объекта на участке между преобразователями, величина M[h²] равна среднеарифметическому значению квадрата толщины стенки M [ h 2 ] = 1 L ∫ 0 L h ( x ) ) 2 d x .

Как правило, на контролируемых объектах дисперсия значений толщины стенки мала по сравнению с квадратом толщины стенки

Если при некотором значении частоты f₁, значении толщины, равном среднеарифметическому значению толщины стенки M[h], типе волны Лэмба G и порядковом номере волны Лэмба i справедливо, что зависимость значений обратной величины эталонной групповой скорости волны Лэмба от произведения толщины и частоты близка к линейной или, другими словами, значение производной второго порядка обратной величины эталонной групповой скорости волны Лэмба по произведению толщины и частоты ∂ 2 ( C G i − 1 ( f ⋅ h ) ) ∂ ( f ⋅ h ) 2 | f 1 ⋅ M [ h ] много меньше по абсолютной величине частного значения обратной величины эталонной групповой скорости и квадрата произведения толщины и частоты C G i − 1 ( f 1 ⋅ M [ h ] ) ( f 1 ⋅ M [ h ] ) 2 , то в силу (2) значение производной второго порядка обратной величины эталонной групповой скорости по произведению толщины и частоты ∂ 2 ( C G i − 1 ( f ⋅ h ) ) ∂ ( f ⋅ h ) 2 | f 1 ⋅ M [ h ] много меньше по абсолютной величине частного значения обратной величины эталонной групповой скорости и произведения дисперсии значений толщины и квадрата частоты C G i − 1 ( f 1 ⋅ h ) ( f 1 2 ⋅ D [ h ] ) .

В этом случае выражение (1) упрощается до

Определение по известным значениям t G i , f₁ и L величины М[h], удовлетворяющей уравнению (3), позволяет получить среднеарифметическое значение толщины стенки.

Если при некотором значении частоты f₂, значении толщины, равном среднеарифметическому значению толщины стенки M[h], типе волны Лэмба G′ и порядковом номере волны Лэмба j справедливо, что зависимость значений обратной величины эталонной групповой скорости волны Лэмба от произведения толщины и частоты существенно нелинейна или, другими словами, значение производной второго порядка обратной величины эталонной групповой скорости волны Лэмба по произведению толщины и частоты ∂ 2 ( C G j ' − 1 ( f ⋅ h ) ) ∂ ( f ⋅ h ) 2 | f 2 ⋅ M [ h ] сравнимо по порядку величины или превосходит по абсолютной величине частное значения обратной величины эталонной групповой скорости и квадрата произведения толщины и частоты C G j ' − 1 ( f 2 ⋅ M [ h ] ) ( f 2 ⋅ M [ h ] ) 2 , то приближение (3) перестает выполняться, и следует использовать общее уравнение (1). Из (1) следует:

Из (4) следует, что имея среднеарифметическое значение толщины стенки M[h], значения второй частоты f₂, времени t G 2 ' и расстояния между преобразователями L можно определить дисперсию значений толщины стенки D[h] по формуле

Наличие среднеарифметического значения толщины M[h] и дисперсии значений толщины D[h] позволяет установить минимальное значение толщины стенки объекта h_min, к примеру, по формуле

h min = M [ h ] − D [ h ] .

Способ контроля за динамикой изменения толщины стенки контролируемого объекта, включающийразмещение на его поверхности на известном расстоянии друг от друга, по крайней мере, одного акустического преобразователя для излучения волн Лэмба и, по крайней мере, одного преобразователя для их приема,излучение в заданный момент времени импульсного сигнала,расчет зависимости спектральной плотности мощности принятого сигнала от времени,выбор волны Лэмба и частоты,определение разности между временем приема выбранной частотной составляющей выбранной волны Лэмба и временем излучения сигнала,определение значения групповой скорости выбранной частотной составляющей выбранной волны Лэмба по известному значению расстояния между преобразователями и значению разности между временем приема выбранной частотной составляющей выбранной волны Лэмба и временем излучения сигнала,определение значения толщины стенки по полученному значению групповой скорости, выбранному значению частоты и эталонной зависимости групповой скорости выбранной волны Лэмба от произведения толщины стенки и частоты,отличающийся тем, чтоустанавли