Способ измерения резонансной частоты

Способ измерения резонансной частоты

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может быть использовано для высокоточного определения резонансной частоты различного типа резонаторов, а также величин, которые функционально связаны с резонансной частотой резонаторов, входящих в состав частотных датчиков и применяемых в различных областях техники и научных исследованиях. В частности, оно может быть использовано в радиочастотных резонансных датчиках влагосодержания нефтепродуктов, концентрации растворов и резонансных уровнемерах различных сред.

Известны различные способы измерения резонансной частоты. Широкое применение получил способ, реализованный в устройстве (SU 1758510 А1, 30.08.1992), которое выполнено на базе экстремального регулятора. В этом устройстве высокочастотный генератор, управляемый напряжением (ГУН), автоматически настраивается на резонансную частоту радиочастотного датчика и отслеживает все ее изменения. При этом частота высокочастотного генератора осциллирует около максимума амплитудно-частотной характеристики (АЧХ) этого датчика и усредненное значение этой частоты считается резонансной частотой этого датчика.

Указанный способ имеет следующие недостатки:

1) АЧХ резонатора должна быть только с одним максимумом, так как при наличии других, локальных максимумов возможно ложное срабатывание и захват локального максимума вместо основного.

2) Погрешность измерения резонансной частоты существенно зависит как от амплитуды входного сигнала, так и от порога срабатывания компаратора, входящего в состав указанного устройства, а также от стабильности этого порога.

3) При измерении резонансной частоты с использованием перестраиваемых генераторов на выходе резонатора наблюдается динамическая резонансная кривая, максимум которой сдвинут относительно максимума статической резонансной кривой, что приводит к дополнительной погрешности измерения резонансной частоты. Этот сдвиг объясняется наличием переходного процесса в резонаторе при перестройке частоты возбуждения, и величина этого сдвига s определяется по формуле (Харкевич А.А. Спектры и анализ. М.: Государственное издательство технико-теоретической литературы. 1957, стр.143)

s = 8 λ / ( f r 2 d 2 ) ,           ( 1 )

где λ - скорость изменения частоты генератора;

f_r - резонансная частота;

d - затухание резонатора.

Наиболее близким к предлагаемому способу по технической сущности является способ измерения резонансной частоты, описанный в устройстве (RU 2427805 C1, 27.08.2011) и принятый в качестве прототипа. Согласно этому способу с помощью синтезатора частоты, управляемого микропроцессором, в резонаторе (чувствительном элементе радиочастотного датчика) возбуждаются колебания с частотой, изменяющейся дискретно с заданным шагом в диапазоне изменения резонансной частоты этого резонатора. На выходе резонатора амплитуда этих колебаний преобразуется в цифровую форму с помощью аналого-цифрового преобразователя (АЦП) и затем эта амплитуда и соответствующая ей частота фиксируются с помощью микропроцессора. После этого микропроцессор определяет максимум напряжения на выходе резонатора и соответствующую этому максимуму частоту, которую принимают равной резонансной частоте.

Недостатком способа-прототипа, реализованного в указанном устройстве, является наличие существенной погрешности измерения резонансной частоты, обусловленной дискретностью перестройки частоты синтезатора, наличием шумов на выходе резонатора и переходными процессами, возникающими в резонаторе при его возбуждении. Погрешность дискретности Δ_d является систематической и зависит от шага перестройки частоты Δ_f. Максимальное значение этой погрешности составляет

Δ d = Δ f / 2.           ( 2 )

Задачей настоящего изобретения является расширение арсенала технических средств.

Техническим результатом изобретения является уменьшение погрешности измерения резонансной частоты, обусловленной дискретностью частот возбуждения, наличием шумов и влиянием переходных процессов.

Указанный технический результат достигается тем, что предлагаемый способ измерения резонансной частоты резонатора, характеризующийся тем, что периодически на вход резонатора подают колебания с частотой, изменяющейся дискретно с заданным шагом в диапазоне изменения измеряемой резонансной частоты, фиксируют дискретную амплитудно-частотную характеристику (АЧХ) резонатора и определяют экстремум этой АЧХ и соответствующую этому экстремуму частоту, которую принимают равной резонансной частоте, при этом формируют случайный сигнал, которым модулируют колебания, подаваемые на вход резонатора, дискретно изменяют частоту этих колебаний в прямом и обратном направлении по симметричному закону, фиксируют в каждом полупериоде этих изменений экстремум АЧХ резонатора и соответствующую этому экстремуму частоту и определяют резонансную частоту как среднее значение зафиксированных частот экстремумов за n-ое количество периодов указанных изменений, которое рассчитывают по формуле

n ≥ ( Δ f / δ a ) 2 / 8 ,           ( 3 )

где Δ_f - шаг перестройки частоты колебаний, подаваемых на вход резонатора;

δ_a - требуемая абсолютная погрешность определения резонансной частоты. При этом случайным сигналом дополнительно модулируют амплитуду колебаний, подаваемых на вход резонатора, или все дискретные частоты этих колебаний.

Предлагаемое изобретение поясняется следующими рисунками.

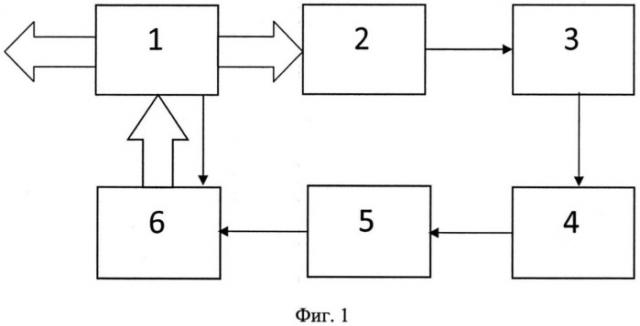
Фиг.1 - структурная схема устройства, реализующего предлагаемый способ.

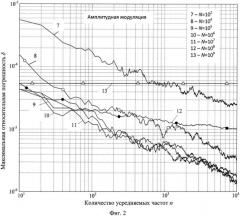
Фиг.2 - графики экспериментальных зависимостей максимальной относительной погрешности измерения резонансной частоты предлагаемым способом от количества усредняемых частот при использовании амплитудной модуляции (AM) случайным сигналом для различных значений отношения сигнал/шум N на выходе резонатора.

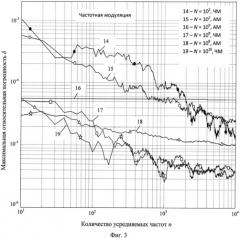
Фиг.3 - графики экспериментальных зависимостей максимальной относительной погрешности измерения резонансной частоты предлагаемым способом от количества усредняемых частот при использовании частотной модуляции (ЧМ) случайным сигналом всех возбуждаемых в резонаторе дискретных частот для различных значений отношения сигнал/шум N на выходе резонатора.

Сущность предлагаемого изобретения заключается в том, что на вход резонатора периодически подается сигнал, частота которого дискретно изменяется в прямом и обратном направлениях в заданном диапазоне f_min÷f_max с шагом Δ_f, и в каждом полупериоде частотной модуляции фиксируется дискретная АЧХ этого резонатора (например, при помощи микропроцессора). При однократном определении резонансной частоты по экстремуму такой АЧХ возникает систематическая погрешность дискретности Δ_d, максимальное значение которой определяется по формуле (2) и погрешность s, возникающая вследствие сдвига резонансной частоты, обусловленного влиянием переходных процессов (формула (1)).

Очевидно, что сдвиг резонансной частоты s, возникающий при каждом сканировании АЧХ резонатора, имеет одинаковую величину и разные знаки при условии, что дискретная зависимость частоты колебаний от времени, подаваемых на вход резонатора, является симметричной. Поэтому усреднение зафиксированных частот, соответствующих экстремумам АЧХ в каждом полупериоде этого сканирования, за n-е число периодов сканирования позволяет компенсировать этот сдвиг. Погрешность дискретности Δ_d в свою очередь можно уменьшить путем уменьшения шага Δ_f, однако это не всегда целесообразно, поскольку при этом увеличивается время измерения и возрастают требования к объему памяти и производительности микропроцессора, производящего различные операции по формированию сетки частот возбуждающего сигнала и обработке сигнала, поступающего с выхода резонатора на этот микропроцессор. Погрешность Δ_d можно сделать случайной, если сигнал, подаваемый на вход резонатора, промодулировать по амплитуде случайным сигналом. И тогда, если истинный резонанс не совпадает ни с одной из дискретных частот, возбуждаемых в резонаторе, то в каждом полупериоде сканирования по случайному закону будут фиксироваться экстремумы и соответствующие им частоты, находящиеся на оси частот выше или ниже от этого резонанса. Среднее значение этих частот будет приблизительно совпадать с истинным значением резонансной частоты с погрешностью δ_a, выражение для которой может быть получено из (3)

δ a = Δ f / ( 2 2 n ) ,           ( 4 )

где n - количество периодов сканирования, участвующих в усреднении (количество усредняемых частот = 2n).

(Маркин Н.С. Основы теории обработки результатов измерений, М.: Издательство стандартов, 1991, стр.93).

Как видно из (4), путем увеличения n погрешность δ_a можно сделать сколь угодно малой.

Оптимальный интервал изменения величины случайного модулирующего сигнала Δ_a при использовании равномерного закона распределения можно определить как изменение АЧХ относительно экстремума при изменении частоты входного сигнала на величину шага Δ_f. Выражение для Δ_a может быть выведено из известного уравнения, описывающего АЧХ резонатора A(f), выполненного в виде параллельного LC-контура,

A ( f ) = A m / 1 + Q 2 ( f / f 0 − f 0 / f ) 2 ,           ( 5 )

где A_m - максимальное значение АЧХ резонатора при резонансе;

Q - добротность резонатора;

f, f₀ - текущая и резонансная частота соответственно.

(Лосев А.К. Линейные радиотехнические цепи. М.: Высшая школа. 1971, стр.230).

Используя разложение выражения (5) в ряд Тейлора относительно переменной f в точке f₀, формулу для Δ_a можно представить в виде

Δ a = 1 / 2 ! A " ( f 0 ) Δ f 2 = 2 A m Δ f 2 Q 2 / f 0 2 ,             ( 6 )

Удобнее использовать отношение сигнал/шум, оптимальное значение которого N_opt для данного случая исходя из (6) определяется как

N o p t = A m / Δ a = f 0 2 / ( 2 Δ f 2 Q 2 ) .             ( 7 )

Можно использовать также в качестве модулирующего случайный сигнал с нормальным законом распределения, и тогда в формулу (6) вместо Δ_a необходимо подставить величину 3σ (где σ - среднеквадратическое отклонение случайного сигнала). И тогда

σ = 2 A m Δ f 2 Q 2 / ( 3 f 0 2 ) .           ( 8 )

Для сокращения времени измерения и экономии вычислительных ресурсов весь диапазон f_min÷f_max обычно сканируется только один раз при запуске процесса измерения. За это первое сканирование находится экстремум АЧХ и соответствующая ему частота f_r1. Последующие сканирования в прямом и обратном направлении производятся в узком диапазоне, симметрично расположенном в окрестности частоты f_r1. В результате этих сканирований определяются частоты f_rj, соответствующие экстремумам АЧХ в каждом полупериоде сканирования (за полный период производится сканирование в прямом и обратном направлении), и резонансная частота f_r вычисляется затем по формуле

f r = 1 2 n ∑ j = 1 2 n f r j .           ( 9 )

где n - число полных периодов сканирования.

Уменьшения погрешности дискретности Δ_d можно также достигнуть, если в каждом полупериоде сканирования изменять по случайному закону все дискретные частоты f_i сигнала, подаваемого на вход резонатора. Выражение для этих частот f_i тогда можно представить в виде

f i = f 1 + δ f + i Δ f ,     i = 1 , 2 , … , m ,           ( 10 )

где δ_f - случайная величина, распределенная по равномерному закону в интервале [0,Δ_f];

m - количество дискретных частот, возбуждаемых за полупериод сканирования;

f₁ - начальная частота.

Как видно из выражения (10), в каждом полупериоде сканирования все частоты f_i сдвигаются на случайную величину δ_f. При этом шаг перестройки частоты Δ_f остается постоянным. Резонансная частота определяется здесь так же, как и для случая амплитудной модуляции случайным сигналом по формуле (9). Преимуществом использования частотной модуляции случайным сигналом является то, что при этом величина δ_f не зависит от параметров резонатора, которые зачастую бывают неизвестны.

Предлагаемый способ может быть реализован по схеме устройства, представленной на фиг.1 и состоящей из цифрового сигнального процессора (ЦСП) 1, синтезатора частоты (СЧ) 2, фильтра низких частот (ФНЧ) 3, исследуемого резонатора 4, амплитудного детектора 5 и аналого-цифрового преобразователя (АЦП) 6.

Указанное устройство работает следующим образом. ЦСП 1 формирует интервалы дискретизации Δt и соответствующие коды для управления частотой СЧ 2 и АЦП 6, а также генерирует случайную числовую последовательность, которой в зависимости от выбранного режима модулируется амплитуда или дискретные частоты сигнала СЧ 2. Эти коды периодически через интервалы Δt подаются на вход СЧ 2 и дискретно изменяют частоту генерируемого им сигнала в прямом и обратном направлении с шагом Δ_f в заданном диапазоне. Одновременно эти коды запоминаются в ЦСП 1. От ЦСП 1 также поступают коды на управляющий вход АЦП 6 для получения выборок в определенные моменты времени, соответствующие установившемуся режиму в исследуемом резонаторе. Далее сигнал с выхода СЧ 2 поступает на вход ФНЧ 3, который предназначен для подавления гармоник и других составляющих спектра, присутствующих в выходном сигнале СЧ 2. С выхода ФНЧ 3 высокочастотный сигнал поступает на вход исследуемого резонатора 4, и затем на детектор 5, который выделяет напряжение огибающей высокочастотного сигнала, которая повторяет АЧХ исследуемого резонатора. Напряжение огибающей поступает на вход АЦП 6 и в заданные моменты времени преобразуется в цифровой код. От АЦП 6 коды выборок напряжения огибающей поступают на ЦСП 1, где накапливаются вместе с соответствующими кодами частот, генерируемых СЧ. В процессе каждого сканирования ЦСП 1 запоминает дискретную АЧХ резонатора 4, находит экстремум этой АЧХ и соответствующую ему частоту f_rj и вычисляет среднее значение этих частот f_r за n сканирований по формуле (9). При этом каждое сканирование осуществляется сигналом, дополнительно модулированным по амплитуде или частоте случайными числовыми последовательностями.

Эффективность предлагаемого способа была подтверждена экспериментом с созданной в среде Matlab виртуальной моделью резонатора, АЧХ которого приближенно описывается выражением (5). Для резонатора с параметрами f₀=14,6 МГц и Q=22 была рассчитана дискретная АЧХ с шагом Δ_f=1,6 кГц. Эта АЧХ в цифровом виде представляет собой два одномерных массива данных, содержащих значения амплитуд (массив A) и частот (массив F). Каждый из этих массивов имеет размер m (m - количество зафиксированных дискретных частот или соответствующих им значений амплитуды на выходе резонатора 4). Для имитации амплитудной модуляции был программно сгенерирован двумерный массив случайных чисел В размера 2n×m. Эти случайные числа были распределены по равномерному закону и изменялись в интервале [0,Δ_a]. Массив В суммировался с массивом значений А, и таким образом был получен массив случайных чисел M=A+B. В каждой j-ой строке массива M определялось максимальное значение амплитуды и соответствующая этому значению частота f_rj и затем вычислялось среднее значение этих частот f_r в соответствии с (9). Далее определялась относительная погрешность определения резонансной частоты δ по формуле

δ = | f r − f 0 | / f 0 .           ( 12 )

Для каждого значения n этот процесс повторялся 20 раз, из полученных реализаций выбиралось максимальное абсолютное значение погрешности δ и строился график зависимости этой максимальной погрешности от количества усредняемых частот для различных значений отношения сигнал/шум N (фиг.2). Из фиг.2 видно, что погрешность δ может быть существенно снижена при увеличении числа усредняемых частот. При этом минимум погрешности δ достигается при значениях N=N_opt=10⁵÷10⁷, которым соответствуют кривые 9÷11. Расчетное значение N_opt для этого случая, рассчитанное по формуле (7), составляет ~10⁵. Как видно из фиг.2, при N<N_opt (N=10², 10⁴ и соответственно кривые 7 и 8) и при N>N_opt (N=10⁸, 10⁹ и соответственно кривые 12, 13) погрешность измерения существенно ухудшается. Следует отметить, что для N≥10⁹ (кривая 13) погрешность δ соответствует формуле (2) и уже не зависит от числа усредняемых частот.

При дополнительной частотной модуляции генерируемых дискретных частот формировался одномерный массив случайных чисел δ_f размера 2n, равномерно распределенных в интервале [0,Δ_f]. В каждом полупериоде сканирования все частоты массива F сдвигались на соответствующее значение величины δ_f. Далее так же, как и для случая амплитудной модуляции находилось максимальное значение амплитуды в каждом полупериоде и соответствующая этому значению частота f_rj. Частоты f_rj затем усреднялись, определялась максимальная погрешность δ и также строился график зависимости этой погрешности от количества усредняемых частот для различных значений N на выходе резонатора 4 (фиг.3). На фиг.3 изображены кривые, полученные как для случая частотной модуляции (кривые 14, 17 и 19), так и кривые для случая AM (кривые 15, 16 и 18). Сравнение этих кривых показывает, что при значениях N≤N_opt=10⁵ оба метода дают примерно одинаковые результаты (кривые 14, 15), но при N>N_opt метод ЧМ обеспечивает более высокую точность, чем метод AM (кривые 16-19).

1. Способ измерения резонансной частоты резонатора, характеризующийся тем, что периодически на вход резонатора подают колебания с частотой, изменяющейся дискретно с заданным шагом в диапазоне изменения измеряемой резонансной частоты, фиксируют дискретную амплитудно-частотную характеристику (АЧХ) резонатора и определяют экстремум этой АЧХ и соответствующую этому экстремуму частоту, которую принимают равной резонансной частоте, отличающийся тем, что формируют случайный сигнал, которым модулируют колебания, подаваемые на вход резонатора, дискретно изменяют частоту этих колебаний в прямом и обратном направлении по симметричному закону, фиксируют в каждом полупериоде этих изменений экстремум АЧХ резонатора и соответствующую этому экстремуму частоту и определяют резонансную частоту как среднее значение зафиксированных частот экстремумов за n-е количество периодов указанных изменений, которое рассчитывают по формулеn≥(Δ_f/δ_a)²/8,где Δ_f - шаг перестройки частоты колебаний, подаваемых на вход резонатора;δ_a - требуемая абсолютная погрешность определения резонансной частоты.

2. Способ по п.1, отличающийся тем, что модулируют случайным сигналом амплитуду колебаний, подаваемых на вход резонатора.

3. Способ по п.1, отличающийся тем, что модулируют случайным сигналом все дискретные частоты колебаний, подаваемых на вход резонатора.