Способ управления программным разворотом разгонного блока

Способ управления программным разворотом разгонного блока

Иллюстрации

Показать все

Реферат

Изобретение относится к ракетно-космической технике, а именно к способам управления движением разгонных блоков (РБ), обеспечивающих довыведение космических аппаратов (КА) с опорной орбиты на целевую (как правило, геостационарную) орбиту, осуществление межорбитальных переходов и других операций с КА.

В космической технике известен выбранный в качестве прототипа способ управления программным разворотом разгонного блока с помощью неподвижных двигателей ориентации постоянной тяги, заключающийся в выполнении набора угловой скорости - разгоне, движении по инерции, уменьшении угловой скорости до нуля - торможении и импульсном включении двигателей ориентации при уменьшении угловой скорости ниже заданного уровня (см. [1]).

Известный способ управления программным разворотом позволяет осуществить плоский программный разворот РБ на заданный угол за заданное время с минимально возможным расходом топлива двигателями ориентации. При этом программный разворот, как правило, совершается на пассивном участке траектории выведения, когда компоненты топлива в баках РБ находятся в состоянии невесомости и не оказывают существенного влияния на динамику разворота. Однако известный способ управления не обеспечивает желаемого качества управления на активных участках, когда включены двигатели поджатия, создающие тягу в направлении продольной оси РБ. Циклограмма функционирования РБ предполагает многократное включение двигателей поджатия для осаждения компонентов топлива к днищам баков для проведения дренирования баков и запуска маршевых двигателей. При этом часто возникает необходимость осуществления программного разворота РБ на участке полета с работающими двигателями поджатия. В этом случае большие массы компонентов топлива оказываются поджатыми к нижним днищам топливных баков и во время выполнения программного разворота совершают поперечные колебания, оказывая на боковые стенки баков значительные силовые воздействия. Обычно баки располагаются в хвостовой части РБ, при этом центр масс РБ смещен к носовой части, в которой находится выводимый на орбиту достаточно массивный КА. Поэтому поперечные колебания компонентов топлива создают существенные возмущающие моменты, величины которых сравнимы с величиной управляющего момента, создаваемого двигателями ориентации. В результате процесс разворота при использовании известного способа управления сопровождается значительным «забросом» по углу (перерегулированием) и повышенной колебательностью, приводящими к увеличению расхода топлива двигателями ориентации.

Задачей предлагаемого изобретения является разработка способа управления программным разворотом разгонного блока, обеспечивающего на участке работы двигателей поджатия выполнение разворота РБ на заданный угол без перерегулирования с одновременным гашением колебаний компонента топлива, оказывающего наибольшее влияние на динамику программного разворота. Например, для существующих в настоящее время и разрабатываемых криогенных разгонных блоков таким компонентом топлива является окислитель (жидкий кислород), масса которого в несколько раз превосходит массу горючего, при этом из-за особенностей конструктивного расположения бака окислителя создается большое плечо гидродинамической силы относительно центра масс РБ.

Техническим результатом предлагаемого изобретения является оптимизация циклограммы функционирования РБ за счет расширения возможностей системы управления в части совмещения различных полетных операций.

Указанный технический результат достигается тем, что в способе управления программным разворотом разгонного блока с помощью неподвижных двигателей ориентации постоянной тяги, заключающемся в выполнении набора угловой скорости - разгоне, движении по инерции, уменьшении угловой скорости до нуля - торможении и импульсном включении двигателей ориентации при уменьшении угловой скорости ниже заданного уровня, в соответствии с изобретением в случае осуществления программного разворота, совмещенного по времени с работой двигателей поджатия, перед разворотом измеряют уровень h наиболее влияющего на динамику разворота компонента топлива в баке, а в процессе разворота периодически измеряют рассогласование по углу Δϑ и угловую скорость ϑ ˙ разворота разгонного блока, угол s_ϑ и угловую скорость s ˙ ϑ отклонения поверхности указанного компонента топлива в баке от продольной оси разгонного блока, при этом выключение двигателей ориентации в конце участка разгона осуществляют при достижении параметром x значения f₁(x'), включение двигателей ориентации в начале участка торможения осуществляют при достижении параметром x значения f₂(x'), где f 1 ( x ' ) = − 4 π x ' + x ' | x ' | 2 ; f 2 ( x ' ) = − x ' | x ' | 2 - функции переключения, а параметры x и x' задают в виде линейных функций измеренных углов и угловых скоростей x=k(k₁Δϑ+k₂s_ϑ), x ' = k 1 ϑ ˙ + k 2 s ˙ ϑ с коэффициентами k, k₁, k₂, определяемыми по заранее рассчитанным зависимостям от уровня h компонента топлива в баке.

Сущность предлагаемого изобретения иллюстрируется фиг.1-4.

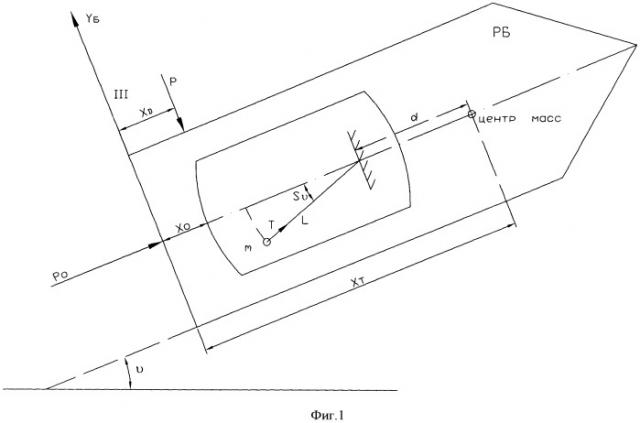
Фиг.1 - Схема разгонного блока при осуществлении программного разворота.

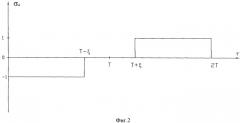
Фиг.2 - Программа управления разворотом в функции безразмерного времени τ.

Фиг.3 - Линии переключения управления в фазовой плоскости безразмерной переменной x и ее производной x' по безразмерному времени τ.

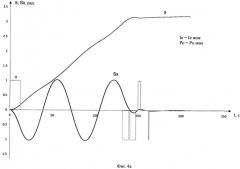
Фиг.4 - Типовые переходные процессы при реализации программного разворота в соответствии с предлагаемым способом управления.

Для управления программным разворотом, совмещенным по времени с работой двигателей поджатия, в математической модели объекта управления необходимо учесть колебания жидких компонентов топлива. В качестве примера рассмотрим математическую модель плоского разворота РБ по тангажу с использованием маятниковой модели, описывающей колебания окислителя в баке. Уравнения пространственного движения РБ как твердого тела с n математическими маятниками выведены в работе [2]. В рассматриваемом случае плоского разворота с одним маятником эти уравнения имеют вид (в предположении малости угла отклонения маятника от положения равновесия)

ϑ ¨ + a 1 s ϑ = μ 1 u         ( 1 )

s ¨ ϑ + a 2 s ϑ = μ 2 u   ,         ( 2 )

где

ϑ - угол тангажа РБ;

s_ϑ - угол отклонения маятника от продольной оси РБ, равный углу отклонения нормали к поверхности окислителя от продольной оси бака;

u - команда на включение управляющих двигателей РБ, принимающая значения - 1, 0, 1;

a 1 = − m P 0 d ( m 0 + m ) I Z ;   μ 1 = P ( x T − x D ) I Z ;         ( 3 )

a 2 = P 0 l ( 1 m 0 + m d ( d + l ) ( m 0 + m ) I Z ) ;   μ 2 = − P l ( 1 m 0 + ( x T − x D ) ( d + l ) I Z ) .         ( 4 )

Здесь (см. фиг.1)

m₀ - масса РБ без учета массы колеблющегося окислителя (масса твердого тела);

I_Z - момент инерции твердого тела;

m - масса материальной точки математического маятника, равная массе колеблющегося окислителя;

P₀ - тяга двигателей поджатия, направленная вдоль продольной оси РБ;

P - тяга одного двигателя ориентации, перпендикулярная продольной оси РБ;

d - расстояние от точки подвеса маятника до центра масс твердого тела;

l - длина нити математического маятника;

x_T - продольная координата центра масс твердого тела в базовой системе координат;

x_D - продольная координата точек приложения сил тяги управляющих двигателей в базовой системе координат.

Система уравнений (1)-(2) имеет следующие начальные и конечные условия

ϑ ( 0 ) = ϑ 0 ; ϑ ˙ ( 0 ) = 0 ; s ϑ ( 0 ) = 0 ; s ˙ ϑ ( 0 ) = 0       ( 5 )

ϑ ( t K ) = ϑ K ; ϑ ˙ ( t K ) = 0 ; s ϑ ( t K ) = 0 ; s ˙ ϑ ( t K ) = 0 ,       ( 6 )

где ϑ₀, ϑ_K - соответственно заданные начальное и конечное значения угла тангажа;

t_K - время окончания разворота.

Перейдем к безразмерным переменным

τ = k t   ;     ( 7 ) x = k ( k 1 Δ ϑ + k 2 s ϑ )   ;     ( 8 ) x ' = k 1 ϑ ˙ + k 2 s ˙ ϑ   ;     ( 9 )

Δ ϑ = ϑ − ϑ K   ;     ( 10 ) y = a 2 s ϑ μ 2 ;     ( 11 ) y ' = a 2 s ˙ ϑ μ 2 ,     ( 12 )

где k = a 2   ;   k 1 = a 2 a 2 μ 1 a 2 − μ 2 a 1   ;   k 2 = − a 1 a 2 μ 1 a 2 − μ 2 a 1 .     ( 13 )

Систему уравнений (1)-(2) и граничные условия (5)-(6) можно представить в виде

x " = u   ;   y " + y = u     ( 14 )

x ( 0 ) = x 0 ; x ' ( 0 ) = 0 ; y ( 0 ) = 0 ; y ' ( 0 ) = 0     ( 15 )

x ( 2 T ) = 0 ; x ' ( 2 T ) = 0 ; y ( 2 T ) = 0 ; y ' ( 2 T ) = 0   ,     ( 16 )

где символы ' и “ означают соответственно первую и вторую производные по безразмерному времени τ, а 2Т - безразмерное время разворота.

Сохраняя известную по способу-прототипу последовательность операций при выполнении программного разворота (разгон, движение по инерции, торможение), выберем временную программу управления в виде, показанном на фиг.2. При этом система (14) за безразмерное время 2Т перейдет из начальных условий (11) в конечные условия, определяемые формулами

x ( 2 T ) = x 0 − σ ( T 2 − ξ 2 )   ;   y ( 2 T ) = 2 σ   cos ( τ − T )   ( cos   T − cos   ξ )   ,     ( 17 )

где σ=signx₀. Чтобы обеспечить выполнение конечных условий (16), достаточно выбрать в качестве безразмерного времени Т одно из значений последовательности

T = | x 0 | 4 π i + π i   ,       ( 18 )

где i=1, 2, 3,…, при этом

ξ = | | x 0 | 4 π i − π i |       ( 19 )

Минимальное безразмерное время разворота обеспечивается при i * = [ | x 0 | + π 2 + π 2 π ] , где квадратные скобки обозначают целую часть числа. Однако при i=i* амплитуда переходного процесса по углу отклонения маятника, моделирующего колебания жидкости в баке, может достигнуть недопустимой величины. Для характерных значений параметров рассматриваемого в примере разгонного блока целесообразно выбрать значение i=2.

Полученные значения параметров T и ξ позволяют реализовать управление программным разворотом, показанное на фиг.2, как функцию времени. Однако для технической реализации целесообразно представить это же управление как функцию переменных состояния x и x', т.е. осуществить синтез управления с обратной связью. Наличие обратной связи, как известно, позволяет компенсировать влияние возмущений, связанных с влиянием внешних факторов, неточным знанием параметров объекта управления и регулятора, неучетом в математической модели второстепенных факторов и др. В предлагаемом способе управления программным разворотом разгонного блока как раз и используется принцип обратной связи. С этой целью были получены уравнения линий переключения в фазовой плоскости (x, x'). При этом отключение двигателя ориентации в конце участка разгона и включение противоположного двигателя ориентации в начале участка торможения осуществляются при достижении параметром x на фазовой плоскости соответственно первой и второй линий переключения (см. фиг.3). Уравнение первой линии переключения имеет вид (для характерных для рассматриваемого РБ значений безразмерного начального условия | x 0 | < 16 π 2 )

f 1 ( x ' ) = − 4 π x ' + x ' | x ' | 2     ( 20 ) ,

а уравнение второй линии переключения

f 2 ( x ' ) = − x ' | x ' | 2     ( 21 ) .

Для реализации такого управления заранее перед полетом РБ вычисляют зависимости коэффициентов (13) линейных функций (8) и (9) от уровня h окислителя в баке. Для этого вначале расчетным путем или экспериментально определяют зависимости от h безразмерных параметров маятниковой модели поведения жидкости: квадрата безразмерной частоты колебаний маятника ω ¯ 2 , безразмерной массы материальной точки маятника m ¯ , безразмерного расстояния от нижнего полюса бака до точки подвеса маятника C ¯ ' [3]. По этим данным определяют длину нити маятника l = R ω ¯ 2 , массу материальной точки маятника m = ρ R 3 m ¯ и расстояние от точки подвеса маятника до центра масс твердого тела d = x T − x 0 − C ¯ ' R − l , где R - характерный размер бака, ρ - плотность окислителя, x_T-х₀ - расстояние от центра масс твердого тела до нижнего полюса бака окислителя. Наконец, по формулам (3), (4), (13) определяют зависимости коэффициентов k, k₁, k₂ от уровня h окислителя в баке. Эти заранее рассчитанные зависимости используются в полете для определения значений коэффициентов. Для этого перед осуществлением программного разворота в соответствии с предлагаемым способом измеряют уровень h окислителя в баке.

Во время выполнения программного разворота периодически измеряют угол ϑ и угловую скорость ϑ ˙ разворота разгонного блока, а также угол s_ϑ и угловую скорость s ˙ ϑ отклонения поверхности окислителя в баке от продольной оси разгонного блока, которые по формулам (8)-(10) пересчитываются в параметры управления x и x'. Измерение углов отклонения поверхности окислителя в баке в двух плоскостях можно осуществить, например, с использованием трех радиоволновых уровнемеров, расположенных на боковой стенке внутри цилиндрического бака под углами в 120°. В частности, могут использоваться уровнемеры «Микрорадар-216Н» [4], имеющие массу не более 3 кг и обеспечивающие измерение уровня жидкости в пределах от 0,5 м до 4 м с точностью ±2,5 мм и частотой выдачи измеренных значений уровня не менее 10 1/с. Угловая скорость отклонения поверхности окислителя в баке от продольной оси разгонного блока может быть получена численным дифференцированием измеренного угла отклонения.

Результаты математического моделирования процесса управления программным разворотом с использованием предлагаемого способа, представленные на фиг.4 (а, б, в) показывают хорошее качество управления как при номинальных значениях характеристик разгонного блока (а), так и при 5%-ных разбросах на значения моментов инерции РБ и тяги двигателей поджатия (б, в).

Таким образом, благодаря реализации предложенного в изобретении технического решения, решается задача управления программным разворотом разгонного блока, обеспечивающего на участке работы двигателей поджатая выполнение разворота РБ на заданный угол без перерегулирования с одновременным гашением колебаний компонентов топлива в баках.

Источники информации

1. Б.В. Раушенбах, Е.Н. Токарь. Управление ориентацией космических аппаратов. М., «Наука», 1974 г., стр.191-194.

2. А.Ш. Альтшулер, В.А. Лобанов. Математические модели пространственных колебаний жидких компонентов топлива в баках ракеты космического назначения на активных участках полета. Авиакосмическая техника и технология. 2010 г., №2, стр.39-46.

3. К.С. Колесников. Динамика ракет. М. «Машиностроение», 2003 г.

4. Уровнемер радиоволновой «Микрорадар-21611» ТУ BY 190460725.003-2009. Руководство по эксплуатации РЭ216Н.000-06. http://www.microradartest.com, , market@microradar.com.

Способ управления программным разворотом разгонного блока с помощью неподвижных двигателей ориентации постоянной тяги, заключающийся в выполнении набора угловой скорости - разгоне, движении по инерции, уменьшении угловой скорости до нуля - торможении и импульсном включении двигателей ориентации при уменьшении угловой скорости ниже заданного уровня, отличающийся тем, что в случае осуществления программного разворота, совмещенного по времени с работой двигателей поджатия, перед разворотом измеряют уровень h наиболее влияющего на динамику разворота компонента топлива в баке, а в процессе разворота периодически измеряют рассогласование по углу Δϑ и угловую скорость разворота разгонного блока, угол s_ϑ и угловую скорость отклонения поверхности указанного компонента топлива в баке от продольной оси разгонного блока, при этом выключение двигателей ориентации в конце участка разгона осуществляют при достижении параметром x значения ƒ₁(x'), включение двигателей ориентации в начале участка торможения осуществляют при достижении параметром x значения ƒ₂(x'), где ; функции переключения, а параметры x и x' задают в виде линейных функций измеренных углов и угловых скоростей x=k(k₁Δϑ+k₂s_ϑ), с коэффициентами k, k₁, k₂, определяемыми по заранее рассчитанным зависимостям от уровня h компонента топлива в баке.