Способ создания многомерных градуировочных моделей аналитического прибора

Способ создания многомерных градуировочных моделей аналитического прибора

Иллюстрации

Показать все

Реферат

Заявляемое изобретение относится к аналитическому приборостроению. В частности, изобретение относится к способам создания градуировочных моделей для различного вида измерительных приборов.

Важными требованиями при проведении анализа свойств тех или иных образцов являются такие требования, как минимизация времени проведения анализа, а также сохранение состава и свойств образцов в процессе измерений. Это особенно важно для промышленных предприятий, где стремятся проводить быстрый неразрушающий контроль свойств продукции на разных стадиях производства. Однако далеко не всегда можно провести измерения требуемых свойств продукции прямыми методами анализа с учетом указанных требований. В таких ситуациях приходится использовать косвенные методы измерения, где анализируемые свойства образцов определяют путем измерения других свойств образцов, зависящих от анализируемых свойств, которые, однако, в отличие от анализируемых свойств могут быть легко измерены напрямую в течение короткого промежутка времени и без разрушения образца. Например, ближняя инфракрасная (БИК) спектроскопия может рассматриваться как один из методов получения косвенной информации об объекте. На основании полученной информации проводят количественный анализ различных объектов, который включает в себя сочетание различных методов исследования многофакторных зависимостей.

Результатом измерения, выполненного с помощью, например, БИК спектрометра (аналитического прибора), является инфракрасный спектр. Под спектром понимают зависимость интенсивности поглощения (отражения или рассеивания) излучения от длины волны в заданном диапазоне. Спектры поглощения (отражения, рассеивания) молекул являются уникальными для каждого вещества, а интенсивность их связана с содержанием поглощающего компонента в исследуемом объекте. Т.о. величина интенсивности полосы поглощения (отражения, рассеивания) может быть связана градуировочной зависимостью с количественным содержанием интересующего вещества в анализируемой пробе. Однако в БИК-спектроскопии используемые количественные связи зачастую слишком сложны. Вызвано это тем, что спектры в БИК-области содержат множество широких перекрывающихся полос поглощения (отражения, рассеивания), которые накладываются на полосу, интересующего нас компонента. Это не позволяет построить простую градуировочную зависимость между интенсивностями характерной полосы с содержанием интересующего вещества. В таком случае формируют многомерную градуировочную модель, которая связывает весь массив спектральной информации с содержанием интересующего компонента.

Для получения информации о количественном содержании интересующего компонента при наличии отградуированного прибора (т.е. прибора с многомерной градуировочной моделью) достаточно заполнить рабочую камеру прибора исследуемым образцом и после регистрации спектра пропускания (отражения, рассеивания), которое занимает несколько секунд или минут, зафиксировать вычисленный по градуировочной модели окончательный результат в цифровом виде в требуемых единицах измерения. При этом одновременно может быть вычислено количественное содержание целого ряда компонентов в исследуемом образце, на определение которых предварительно отградуирован прибор. Например, можно легко определять количественное содержание протеина, влажности и клейковины в зерне пшеницы или других культур. Следует отметить, что данная техника абсолютно безопасна как для оператора, так и для анализируемых образцов. Зерно, которое использовалось для анализа, в дальнейшем вполне пригодно для выращивания из него растений.

Величины, измеряемые непосредственно прибором, называются «первичными свойствами», а анализируемые параметры образцов, от которых зависят результаты измерений, но которые не измеряются непосредственно, называют «вторичными свойствами». Для БИК-анализатора "вторичные" свойства образцов (например, количественное содержание протеина, влажности клейковины и т.д.) определяются по результатам измерений их спектральных характеристик, таких как оптические спектры поглощения, отражения или рассеяния, выступающие в качестве "первичных" свойств.

Для любого непрямого метода анализа свойств образцов очень важным является этап определения математических соотношений (коэффициентов регрессии) между результатами измерений первичных свойств образца и значениями величин, характеризующих анализируемые вторичные свойства. Эти соотношения между измеряемыми на приборе первичными свойствами, которые представляют собой массив данных, и анализируемыми вторичными свойствами образца называются многомерными градуировочными моделями.

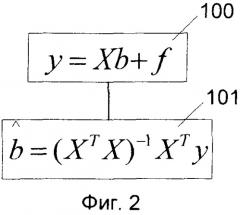
Простейшим методом, позволяющим находить оптимальные коэффициенты регрессии для построения многомерной градуировочной модели, является метод множественной линейной регрессии (МЛР) [3]. На фиг.2 представлена упрощенная схема метода МЛР. В данном методе набор переменных в матрице X объединяется в линейную комбинацию, коррелирующую настолько, насколько это возможно с соответствующими значениями матрицы Y. Таким образом, вычисляется регрессионная зависимость между матрицей Y и матрицей X. В блоке 100 представлено основное уравнение МЛР, в котором матрицы Y и X связаны регрессионными коэффициентами b. Задачей данного метода является нахождение такой матрицы B ∧ , чтобы величина ошибки f была минимальна. В методе МЛР она решается методом наименьших квадратов (блок 101).

Основным недостатком метода МЛР является необходимость обращения матрицы (X^T X) при вычислении B ∧ . Если в матрице X присутствуют коллинеарные данные, то ее обращение оказывается сложной задачей, а в некоторых случаях вообще неразрешимой проблемой. Умножение на (X^T X)^-1 становится неустойчивым и фактически эта операция соответствует делению на ноль. Недостатком метода МЛР является также то, что метод может работать только с ограниченным массивом матрицы первичных свойств X. Если размерность данной матрицы n×p (n - число образцов, p - число переменных в первичных свойствах каждого образца), то существующее ограничение для метода МЛР (p должно быть не больше n-1) существенно ограничивает его применение для градуировки, например, таких приборов, как сканирующие БИК анализаторы, где значение p может быть более 500.

Существенным расширением метода МЛР является метод регрессии на главные компоненты (РГК) [3].

Метод РГК работает в два основных шага.

На первом шаге для сокращения массива данных первичных свойств и исключения мультиколлинеарности их преобразуют, используя метод главных компонент (МГК) так, чтобы вся информация описывалась значительно меньшим числом переменных. МГК позволяет осуществить переход из исходной системы координат в систему координат меньшей размерности. Причем главные компоненты должна быть ортогональны. Уменьшая размерность исходной матрицы первичных свойств, происходит отделение полезной информации от шума. В общем виде разложение матрицы X размерностью n×p записывается в виде: X=TP^T+E,

где T - матрица счетов размерностью n×A, представляющая собой координаты исходных образцов на главных компонентах; P - матрица нагрузок размерностью A×P, представляющая собой набор коэффициентов, связывающих переменные в пространстве главных компонент с переменными в исходном пространстве; A - число главных компонент, выбранных для описания исходных данных. Вычисление матриц T и P осуществляется итерационными методами, например методом NIPALS [4].

На втором шаге вычисляются (с применением метода наименьших квадратов) корреляционные коэффициенты, связывающие вторичные свойства градуировочных образцов с первичными свойствами, отображенными в новом пространстве главных компонент.

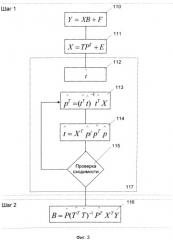
На фиг.3 представлена упрощенная схема метода РГК. В блоке 110 представлено основное уравнение РГК, в котором матрицы Y и X связаны регрессионными коэффициентами B. Задачей метода РГК, так же как и ранее рассматриваемого метода МЛР, является нахождение такой матрицы B ∧ , чтобы величина ошибки F была минимальна. В блоке 111 представлено основное уравнение разложения матрицы первичных свойств X на счета T и нагрузки P. В блоке 117 представлена упрощенная схема МГК по вычислению счетов и нагрузок для каждой главной компоненты. Этапы блока 117 проводятся столько раз, сколько главных компонент определяется для конкретной модели. В блоке 112 в качестве начальных значений вектора счетов i первой компоненты выбирается столбец матрицы X, который имеет наибольшую сумму квадратов отклонений от среднего значения. В блоке 113 представлено решение для уравнения X = t ∧ p T + E по нахождению методом МНК нагрузок p ∧ . В блоке 114 уточняется вектор счетов t ∧ путем решения методом МНК уравнения X = t p ∧ T + E . В блоке 115 оценивается значимость расхождения t ∧ , определенных в блоках 112 и 114. Если расхождение значимо - то идет возврат в блок 113, в котором для вычисления p ∧ используются счета, полученные в блоке 114. Если расхождение не значимо - то повторяются все операции блока 117 заново для следующей главной компоненты, при этом в качестве матрицы первичных свойств берется матрица ошибок, определяемая как X − t ∧ p ∧ T . Когда вычислены счета и нагрузки для всех главных компонент - вычисляется матрица регрессионных коэффициентов B ∧ методом МНК (блок 116) для уравнения Y = T ∧ B T + E .

РГК в отличие от МЛР снимает проблему коллениарности данных (первичных свойств). РГК позволяет работать с существенно большим количеством данных в отличие от МЛР.

Недостатком метода РГК является то, что декомпозиция матрицы X не обязательно приведет к выделению именно той структуры, которая коррелирует с искомыми свойствами Y. Заранее нет никакой уверенности в том, что количество используемых главных компонент будет содержать только ту информацию, которая коррелирует с интересующей нас переменной Y. В выбранных компонентах могут присутствовать и другие источники изменения первичных свойств, а в старших компонентах может остаться часть информации, которая коррелирует с переменной Y, т.е. со вторичными свойствами. Это обстоятельство может снижать точность выполняемых измерений. Также использование градуировочной модели, построенной с применением метода РГК, при выполнении непосредственного анализа неизвестного образца предполагает разложение вектора первичных свойств этого образца в пространстве главных компонент, что требует определенных вычислительных мощностей при рутинном анализе.

Широкое применение нашел метод проекции на латентные структуры (ПЛС), имеющий альтернативное название как метод дробных наименьших квадратов [3]. На фиг.4 представлена упрощенная схема метода ПЛС. В блоке 120 представлено основное уравнение ПЛС, в котором матрицы Y и X связаны регрессионными коэффициентами B. Задачей метода ПЛС, так же как и методов РГК и МЛР, является нахождение такой матрицы B ∧ , чтобы величина ошибки F была минимальна. Метод ПЛС, так же как и метод РГК, можно разделить на два шага. На первом шаге методом МГК проводится декомпозиция не только матрицы первичных свойств X на счета T и нагрузки P, но и матрицы вторичных свойств Y на счета T и нагрузки Q (блоки 121 и 122). Но это не два независимых друг от друга разложения, а взаимосвязанные процессы. Особенности вычисления счетов и нагрузок для обоих разложений схематично представлены в блоке 131. Этапы блока 131 проводятся столько раз, сколько главных компонент определяется для конкретной модели. Расчет оптимальных значений счетов и нагрузок для матриц X и Y осуществляется следующим образом. В блоке 123 в качестве начальных значений вектора счетов t ∧ первой компоненты выбирается столбец u ∧ матрицы вторичных свойств Y, который имеет наибольшую сумму квадратов отклонений от среднего значения. Данный вектор u ∧ используется для определения взвешенных нагрузок w ∧ матрицы X. Нахождение вектора w ∧ (блок 124) осуществляется методом МНК для уравнения X = u ∧ w T + E . В блоке 125 представлено решение метода МНК по определению счетов t ∧ на основании уравнения X = t w ∧ T + E . В блоке 126 вычисляются нагрузки p ∧ методом МНК из уравнения X = t ∧ p T + E . Далее вычисляются нагрузки для матрицы вторичных свойств Y, увязывая их со счетами, определенными в блоке 125. В блоке 127 представлено решение методом МНК по нахождению нагрузок q ∧ из уравнения Y = t ∧ q T + E . В блоке 128 уточняется вектор счетов u ∧ путем решения методом МНК уравнения Y = u q ∧ T + E . В блоке 129 оценивается значимость расхождения u ∧ , определенных в блоках 123 и 128. Если расхождение значимо - то идет возврат в блок 124, в котором для вычисления w ∧ используются счета, полученные в блоке 128. Если расхождение не значимо - то повторяются все операции блока 131 заново для следующей главной компоненты при этом в качестве матрицы первичных свойств берется матрица ошибок, определяемая как X − t ∧ p ∧ T , а в качестве матрицы вторичных свойств берется матрица ошибок, определяемая как: Y − t ∧ p ∧ T . Когда вычислены счета и нагрузки для всех главных компонент - вычисляется матрица регрессионных коэффициентов B ∧ (блок 130) методом МНК.

Данный метод существенно отличается от методов МЛР и РГК. В ПЛС скрытые переменные связываются как с первичными, так и с вторичными свойствами. Причем эта связь осуществляется так, чтобы как можно большая часть дисперсии первичных свойств была максимально связана со вторичными свойствами. Это может повышать точность градуировочной модели, а также приводит к тому, что при построении модели используется меньшее число главных компонент, чем в РГК. Однако метод ПЛС, так же как и РГК, не идеален. При декомпозиции данных с помощью МГК отбрасывается часть информации, которая может быть полезна при построении модели. Метод ПЛС требует значительной квалификации исследователя, так как сложен в обращении.

Известны [5] также методы математического программирования (МП), которые могут быть использованы, как указано в [6], для поиска регрессионных коэффициентов, связывающих два массива данных, при минимизации значения ошибки регрессионного уравнения.

Известны решения задач квадратичного математического программирования [7], которые можно использовать для расчета градуировочной модели, если целевую функцию представить в виде:

g ( b ) = ( Y − X b ) T ( Y − X b ) ,   (1)

где g - вектор, содержащий квадраты ошибки градуировочной модели. Матрица Y описывает, как указывалось выше, вторичные свойства, а матрица X - первичные свойства. Вектор b содержит искомые коэффициенты регрессии. Область поиска экстремальных значений целевой функции определяется некими ограничениями. Коэффициенты регрессии b должны находиться внутри пространства гиперкуба. Гиперкуб - фигура в Евклидовом p-мерном пространстве (p - число переменных в первичных свойствах). Например, если p=3, то гиперкуб - это куб в трехмерном евклидовом пространстве, имеющий длину ребра, равную d. Оптимальные размеры гиперкуба могут определяться с помощью процедуры валидации. Т.е. размерность гиперкуба можно считать оптимальной, если критерии оценки качества градуировочной модели удовлетворяют необходимым условиям.

Целевую функцию g(b) необходимо привести к каноническому виду для последующего поиска коэффициентов регрессии. Для этого производится замена переменных в уравнении для целевой функции:

C = 2 ( X T X )                                    (2)

D = − 2 ( X T Y )                                     (3)

Тогда целевая функция g может быть представлена в следующем каноническом виде:

g ( b ) = D T b + b T C b → min                  (4)

d ≥ b ,     b ≥ 0                                            (5)

Существует много конечных методов решения данной задачи. Например, в качестве эффективного и простого метода решения может быть применен называемый метод решения задач о дополнительности, разработанный Лемке [7].

Упрощенная схема алгоритма построения градуировочной модели с использованием техники математического программирования представлена на фиг.5, в котором задача математического программирования сводится к задаче о дополнительности. В блоке 201 формируется целевая функция и ограничения из уже известного линейного уравнения градуировки, представленного в блоке 200, где вектор b (b₁, b₂, … b_n) содержит указанные выше искомые коэффициенты регрессии, вектор d (d₁, d₂, … d_n) представляет указанное выше пространство ограничений. Систему, сформированную в блоке 201, можно представить как каноническую задачу выпуклого квадратичного программирования (блок 202). Функция Лагранжа для данной задачи записана в блоке 203, где u и ν - множители Лагранжа. Для данной функции Лагранжа, дифференциальные условия Куна-Такера записаны в блоке 204. Произведя замену S=d-b, систему можно представить так, как показано в блоке 205. Представив систему, записанную в блоке 204, в виде набора матриц (блок 205), можно записать эквивалентную задачу о дополнительности (блок 206). Алгоритм решения задачи о дополнительности представлен на фиг.6.

Задача о дополнительности (блок 300) имеет решение, если хотя бы один из элементов q_i<0. Чтобы начать работу алгоритма с начала (w=q, z=0), для получения неотрицательного решения производится преобразование задачи, представленное в блоке 301, где во все уравнения системы вводится искусственная переменная z₀ (при этом e - единичный вектор). Полученную систему можно представить в виде симплекс таблицы (блок 302):

базис	z1	…	zs	…	zk	z0	q
w1	-m11	…	-m1s	…	-m1k	-1	q1
ws	-ms1	…	-mss	…	-msk	-1	qs
wn	-mn1	…	-mns	…	-mnk	-1	qn

В базис вводится z₀, которая заменит базисную переменную. В качестве заменяемой базисной переменной выбирается переменная с наибольшим по абсолютной величине отрицательным значением. Т.е. если q s = min q i < 0 i , то в этом случае z₀ заменит базисную переменную w_s. Все остальные значения в таблице пересчитываются в блоке 305 относительно выбранной строки следующим образом:

q s ' = − q s ,       q i ' = q i − q s ,         i ≠ s                               (6)

m s j ' = m s j ,       j = 1 … k                                              (7)

m i j ' = − m i j + m s j ,       j = 1 … k ,       i ≠ s                                (8)

Таким образом, получается новая симплекс таблица:

базис	z1	…	zs	…	zk	z0	q
w1	m 11 '	…	m 1 s '	…	m 1 k '	0	q 1 '
z0	m s 1 '	…	m s s '	…	m s k '	1	q s '
wn	m n 1 '	…	m n s '	…	m n k '	0	q n '

Далее, в блоке 303 определяется, какая переменная будет выведена из базиса и какая переменная будет введена в базис вместо нее. В базис всегда вводится переменная, дополнительная к базисной переменной, выведенной из базиса на предыдущем шаге. Т.е. если на предыдущем шаге была выведена переменная w_s, то на данном шаге в базис будет вводиться переменная z_s. Переменные w_i и z_i - это пара взаимодополняемых переменных. При определении переменной, которая будет выводиться из базиса, применяется правило минимального соотношения:

min m i s ' > 0 ( q i ' / m i s ' ) = q k ' / m k s '                            (9)

для всех i=1…n, для которых значения m i s i > 0 .

То есть в блоке 303 в базис вводиться переменная z_s вместо переменной w_k, выводимой из базиса. Далее в блоке 304 проверяется условие, является ли выводимая переменная переменной z₀.

Как только в строке S будет выведена переменная z₀, значит в базисе остались только z_i, где i=1…n, и оптимальное решение достигнуто, z_i=q_i, где i=1…n. Искомый вектор регрессионных коэффициентов (блок 306) есть b_i=z_i, где i=1…n.

Следует отметить, что метод математического программирования не использует нестабильных операций, поэтому коллинеарность анализируемых данных не влияет на полученные результаты в отличии от метода МЛР.

Предложенный метод математического программирования с решением задачи о дополнительности обладает значительной устойчивостью, под которой в данном случае понимается способность правильно оценивать направления рабочего движения, а также способность быстро и точно приводить рабочую точку в область экстремума несмотря на наличие помех. Это является большим преимуществом, так как повысить надежность метода наименьших квадратов можно только за счет повышения качества подготовки входных данных. Результаты методов математического программирования можно анализировать на любом этапе вычислений.

Однако применение метода математического программирования, так же как алгоритм МЛР, не может работать с данными, для которых число образцов меньше числа переменных в первичных свойствах, что существенно ограничивает его применение для градуировки, например, таких приборов, как сканирующие БИК анализаторы, где значение p может быть более 500.

Авторы патента [8] показали, что техника математического программирования может эффективно применяться в спектрометрии, при обработке многомерных данных. В патенте представлено устройство для определения наиболее вероятных концентраций компонентов в анализируемом образце. Устройство включает в себя средства для измерения спектральной интенсивности указанной химической смеси, а также средства для вычисления указанных концентраций, средства для хранения данных, для отображения данных и т.д. Для определения концентраций устройство обрабатывает многомерные наборы данных. При этом осуществляется нахождение таких математических соотношений между первичными и вторичными свойствами, чтобы величина ошибки была минимальна. В патенте сказано, что наиболее предпочтительным способом нахождения указанных математических отношений является симплекс метод линейного программирования, так как использование данного метода значительно сокращает время вычисления.

Авторы [9] также предложили использовать метод математического программирования в способе построения многомерной градуировки для БИК анализаторов, применяемых для анализа различных свойств образцов сельскохозяйственной промышленности.

Однако использование метода математического программирования в случаях, предложенных авторами [8] и [9], ограничивает его применение для градуировочных моделей, для которых число образцов меньше числа переменных в их первичных свойствах.

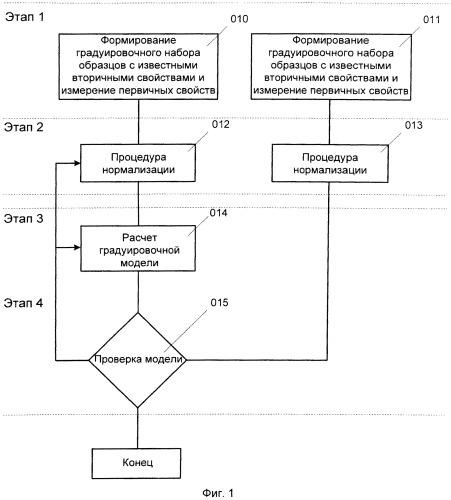
За прототип предлагаемого способа создания многомерных градуировочных моделей аналитического прибора принят способ, изложенный в [1]. Данный способ состоит из поэтапной процедуры расчета градуировочной модели, представлен на фиг 1.

На первом этапе проводится подбор образцов градуировочного и валидационного (проверочного) наборов образцов с известными вторичными свойствами, а также регистрация их первичных свойств (блоки 010 и 011). Вторичные свойства градуировочного и валидационных наборов определяются при помощи независимых референтных методов, имеющих заданную точность и воспроизводимость. Значения вторичных свойств градуировочного и валидационного наборов называются референтными данными. Диапазон изменения вторичных свойств образцов градуировочного и валидационных наборов должен полностью охватывать диапазон возможных изменений этих свойств при последующем анализе неизвестных образцов. Кроме того, для создания наиболее устойчивой модели образцы в градуировочном наборе должны быть однородно распределены в диапазоне изменения анализируемых свойств. Подобные принципы выбора образцов градуировочного и валидационного набора регламентируется, например, в [1]. Таким образом, на первом этапе формируются:

матрица X первичных свойств и матрица Y вторичных свойств (матрица референтных данных) градуировочного набора образцов;

матрица X' первичных свойств и матрица Y' вторичных свойств (матрица референтных данных) валидационного набора образцов.

Валидационный набор обычно отличается от градуировочного меньшим количеством образцов.

На втором этапе для обоих наборов могут быть проведены процедуры предобработки данных. Предобработка представляет собой определенные алгоритмы математического преобразования матрицы X для уменьшения влияния на них различных факторов, не связанных с определяемыми свойствами. Известны, например, следующие виды преобразования данных [2]: выравнивание базовой линии, сглаживание данных (например, с применением фильтра Савицкого-Голея, скользящего среднего и т.п.), взятие производных, центрирование данных, шкалирование данных (нормирование на среднее квадратическое отклонение по каждой переменной), нормирование на среднее квадратическое отклонение по образцу, мультипликативная коррекция и др. Некоторые виды предобработок, например центрирование данных, может применяться, как к матрице X, так и к матрицам X и Y одновременно. Над данными, полученными на этапе 1, может применяться как один определенный алгоритм предобработки, так и несколько алгоритмов в определенной последовательности. Проверка оптимальности выбранных алгоритмов предобработки и последовательности их применения определяется на стадии валидации (этап 4).

Следует отметить, что на градуировочный и валидационный набор накладываются одинаковые алгоритмы предобработок и последовательность их применения (блоки 012 и 013).

На третьем этапе проводится расчет градуировочной модели (блок 014) с использованием предобработанных данных градуировочного набора, заключающийся в нахождении оптимальных соотношений (коэффициентов регрессии) между вторичными (матрица Y) и первичными свойствами (матрица X) градуировочного набора образцов. Этап построения градуировочной модели является наиболее трудоемкой и значимой процедурой в многомерной градуировке и требует от исследователя достаточного опыта и знаний. Для нахождения оптимальных соотношений (коэффициентов регрессии) между вторичными и первичными свойствами образцов применяются различные методы многомерного анализа.

На четвертом этапе проводится проверка созданной модели с применением валидационного набора образцов (блок 015). На данном этапе также могут проводиться и другие виды проверок с использованием, например, перекрестной проверки или проверки на выбросы по оценке расстояния Махаланобиса [2]. По результатам проверки может корректироваться градуировочный набор (отбрасываться аномальные образцы), изменяться предобработки данных, изменяться параметры градуировочной модели.

В качестве методов вычисления регрессионных коэффициентов в [1] предлагается использовать методы МЛР, РГК и ПЛС. Данные методы были описаны выше и, как было показано, имеют определенные недостатки, которые могут влиять на качество градуировочной модели и соответственно точность анализа.

Задачей настоящего изобретения является разработка способа создания градуировочной модели для определения одного или нескольких вторичных свойств неизвестного образца, по результатам измерения множества первичных свойств этого образца, не обязательно спектральных, который обеспечивает большую точность определения анализируемых свойств.

Предложенный способ создания многомерных градуировочных моделей аналитического прибора включает в себя: подбор градуировочного и валидационного наборов образцов с известными вторичными свойствами, определенными референтными методами; измерение на аналитическом приборе первичных свойств каждого из образцов обоих наборов для формирования матриц первичных свойств этих наборов; преобразование матриц первичных свойств процедурами предобработок обоих наборов, построение градуировочной модели путем нахождение оптимальной матрицы коэффициентов регрессии, связывающей вторичные свойства образцов градуировочного набора через измеренные на аналитическом приборе первичные свойства методами многомерного анализа; проверку градуировочной модели процедурами валидации с использованием образцов валидационного набора, причем перед построением градуировочной модели проводят нормировку предобработанных первичных свойств на максимальное значение первичных свойств образцов градуировочного набора с по