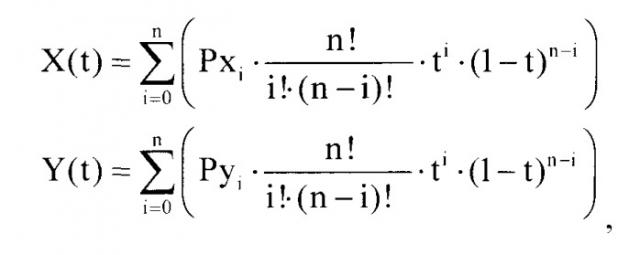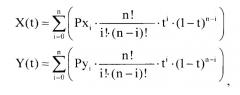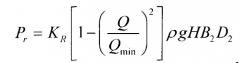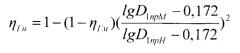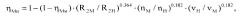Способ проектирования центробежных насосов

Способ проектирования центробежных насосов

Иллюстрации

Показать все

Реферат

Изобретение относится к области машиностроения, а именно проектированию центробежных насосов, предназначенных, в частности, для использования в качестве нефтяных магистральных насосов.

Нефтяные магистральные насосы имеют, как правило, большую мощность и, соответственно, потребляют много энергии. При этом в суммарной стоимости жизненного цикла насоса затраты на электроэнергию могут достигать 80%. Отсюда даже незначительное повышение КПД насоса на 1-2% может давать существенный экономический эффект. Кроме того, указанные насосы должны обладать высокой надежностью, поскольку простой магистрального оборудования связан с большими экономическими потерями. Отсюда возникает необходимость в повышении энергоэффективности и надежности проектируемых насосов, а также в оптимизации параметров насоса. При этом основные сложности возникают при проектировании проточной части насоса. В настоящее время существует достаточно много методик по расчету и проектированию проточной части центробежных насосов. Однако использование только расчетных методов не позволяет в должной мере решить задачу по оптимизации параметров насосов, даже с привлечением вычислительной техники, реализующей полуавтоматизированные и автоматизированные алгоритмы построения проточных частей центробежного насоса. Дополнение расчетных методов результатами испытаний натурных образцов также не позволяет полностью решить указанную проблему, ввиду больших затрат на изготовление натурных образцов насосов, относящихся к дорогостоящему оборудованию, и проведение их испытаний, т.к. для нахождения оптимальных параметров методом итераций, может возникнуть необходимость в неоднократных изменениях параметров насоса, изготовлении новых натурных образцов и проведении повторных циклов испытаний. Таким образом, процесс оптимизации параметров может затянуться на длительное время и потребовать слишком больших затрат на проектирование насосов, что, соответственно, приведет к прекращению дальнейших работ по выявлению наиболее оптимальных параметров насоса, даже в ущерб его потенциально достижимым качественным характеристикам. Вместе с тем, постоянный рост технических требований к насосному оборудованию настоятельно требует не ограничиваться построением проточной части насоса только на основе расчета по исходным данным, без осуществления при этом оптимизации наиболее важных параметров.

Известен способ проектирования центробежных насосов с использованием системы автоматизированного проектирования проточных частей насоса (ст. Система автоматизированного проектирования проточных частей насосов. Создание новых высокоэкономичных насосов, Лукашевич В.П., сб.тр., М., ВНИИ Гидромащ, 1981, стр.18-21). В данном способе система автоматизированного проектирования использовалась для построения проточной части рабочего колеса с помощью числовых методов.

В процессе дальнейшего совершенствования методов автоматизированного проектирования был разработан способ построения сечений отвода насоса при помощи В-сплайнов в программном комплексе, снабженном графическим интерфейсом (ст. Интерактивная система автоматизированного проектирования отводов динамических насосов с графическим диалогом. Насосы для технологических линий, Устиловский Р.В., сб.тр., М., ВНИИ Гидромащ, 1987, стр.34-41). Указанный способ решал только часть задачи по проектированию проточной части насоса и не обеспечивал решения проблем оптимизации.

Известен способ моделирования в компьютерных системах трехмерного проектирования, при котором на основе полученных для объекта исходных данных создают трехмерную компьютерную модель объекта в виде габаритного имитатора и имитатора массы и главных центральных моментов инерции, затем совмещают начало системы координат имитатора массы и главных центральных моментов с точкой, соответствующей положению центра масс объекта, а оси совмещают с соответствующими направлениями главных центральных осей трехмерной модели объекта (патент RU 2263966, приоритет от 24.02.2004, G06T 17/00). В результате получают компьютерную трехмерную модель объекта в виде массово-инерционного имитатора, после чего определяют массово-центровочные и инерционные характеристики полученной модели. Указанный способ может быть использован при проектировании многокомпонентных изделий с помощью компьютерных систем трехмерного моделирования, но в целом мало пригоден для решения задач по проектированию проточной части насоса.

Известен способ автоматического построения трехмерной геометрической модели изделия в системе геометрического проектирования, при котором выбирают данные компьютерной математической модели, которые будут использованы для построения трехмерной геометрической модели изделия, задают последовательность операций автоматического построения, считывают выбранные пользователем данные, преобразуют считанные данные в значения геометрических параметров изделия, извлекают из предварительно созданной базы данных трехмерные геометрические модели-примитивы, изменяют значения их параметров в соответствии с данными компьютерной математической модели, выполняют динамическое построение элементов изделия, трехмерные геометрические модели-примитивы которых отсутствуют в базе данных, а затем помещают полученные трехмерные геометрической модели элементов изделия в трехмерную геометрическую модель сборки (патент RU 2308763, приоритет от 26.09.2005, G06T 17/40). Трехмерная геометрическая модель изделия строится пользователем на экране монитора, все изменения в модели отображаются на экране монитора при соответствующих командах пользователя. Предложенный способ может быть использован при проектировании проточных, частей насоса, но не решает задач по оптимизации геометрических параметров изделия, а также по верификации полученных результатов.

Известен способ оптимизации проточных частей лопастных гидромашин с использованием метода ЛП-тау поиска (Автоматизированное проектирование гидромашин, Панаиотти С.С., М., МГТУ им. Н.Э. Баумана, стр.24). Указанный способ позволяет повысить качество оптимизации, но также не решает проблему в целом.

При этом все приведенные выше методы построения проточной части насосов не позволяют получить готовую 3-D модель проточной части в короткие сроки, в то время как современные методы проектирования, гидродинамического моделирования и автоматизированные методы организации технологического процесса изготовления основываются на 3-D модели, как на исходной информации.

Технической задачей изобретения является повышение энергоэффективности и надежности проектируемых насосов посредством оптимизации их параметров, а также снижение затрат на проектирование, в том числе на проведение натурных испытаний.

Поставленная задача решается тем, что в отличие от известных способов проектирования центробежных насосов с использованием методов автоматизированного проектирования и математического моделирования предлагаемый способ реализует комплексную методику, согласно которой в процессе построения 3-D модели проточной части насоса осуществляют ее оптимизацию как по потерям энергии, так и по радиальной нагрузке на ротор насоса, изготавливают модель с использованием 3-D принтера, производят гидравлические испытания модели насоса, в процессе которых осуществляют измерение напорных и энергетических характеристик насоса, включая измерение давления в различных точках проточной части насоса, мощности и момента на валу насоса, частоты вращения вала насоса, перепада давлений на насосе, напора и подачи насоса, проводят их статистическую обработку и определяют КПД насоса, после чего на основе теории подобия осуществляют пересчет результатов испытаний на натурные характеристики насоса, сравнивают полученные результаты испытаний с расчетными характеристиками насоса и, при необходимости, осуществляют коррекцию используемой для оптимизации параметров математической модели течения жидкости в насосе, затем сравнивают результаты испытаний с расчетными характеристиками насоса и повторяют указанные операции до достижения совпадения с заданной точностью характеристик насоса, полученных расчетным и экспериментальным путем, после чего определяют геометрические параметры проточной части насоса, изготавливают натурный образец насоса и в процессе испытаний измеряют напорные и энергетические характеристики натурного образца насоса, сравнивают их с заданными и расчетными характеристиками и, при необходимости, корректируют характеристики математической модели проточной части насоса.

Построение 3-D модели проточной части насоса с использованием метода численного моделирования на основе характеристик расчетных сечений, в процессе которого осуществляют оптимизацию проточной части насоса, как по потерям энергии, так и по радиальной нагрузке на ротор насоса, позволяет существенно сократить трудоемкость производимых расчетов и найти вариант 3-D модели проточной части насоса, обладающий наилучшими расчетными характеристиками.

Проведение натурных испытаний изготовленной 3-D модели проточной части насоса позволяет осуществить проверку соответствия характеристик 3-D модели проточной части насоса расчетным и внести в них необходимую коррекцию для их приближения к требованиям технического задания, при этом не только улучшить основные характеристики насосов, но и сократить трудоемкость и стоимость работ по проведению испытаний натурных образцов насоса, без которых нельзя переходить к их производству.

Сущность настоящего изобретения иллюстрируется следующими чертежами:

Фиг.1 - двухзавитковый спиральный отвод;

Фиг.2 - сечение спиральной части отвода;

Фиг.3 - сечение обводного канала отвода;

Фиг.4 - параметризация диффузорной части отвода;

Фиг.5 - построение переходных сечений диффузора;

Фиг.6 - триммированная поверхность отвода.

При проектировании центробежных насосов основную сложность вызывает профилирование их проточной части, где выделяют подвод, рабочее колесо и отвод. Само проектирование начинается с формулирования требований технического задания, определяемых в соответствии с предполагаемыми условиями эксплуатации, а также исходя из существующего практического опыта и имеющихся рекомендаций. При этом задают основные функциональные характеристики насоса, определяющие его производительность, в том числе подачу насоса, напор и частоту вращения вала насоса, и габаритные ограничения, определяющие предельные размеры рабочих органов, прежде всего диаметр рабочего колеса. Затем на их основе определяют набор параметров, характеризующих геометрию рабочего колеса и сечений проточной части насосов и их пропускную способность. При построении сечений проточной части насосов методом численного моделирования сначала определяют характеристики расчетных сечений проточной части на выходе подвода и входе отвода, после чего на основе характеристик расчетных сечений определяют параметры промежуточных сечений проточной части насоса. При этом расчетные параметры сечений проточной части насоса определяют по результатам построения 3-D моделей проточной части насоса, в процессе которого выбирают параметры оптимизации сечений, наиболее сильно влияющих на основные характеристики насоса, включающие потери напора в отводе и суммарную радиальную силу на роторе насоса, задают диапазон изменения для каждого параметра оптимизации, формируют численный массив в пределах выбранных диапазонов их изменений, из которого производят выборку оптимального варианта соотношения значений КПД и радиальной силы на роторе насоса.

Указанные операции реализуются на основе известных средств и методов. Так, например, при проектировании двухзаходного спирального отвода можно выделить три основных параметризируемых элемента: спиральная часть 1, обводной канал 2 и диффузор 3 (Фиг.1). На Фиг.1 также показан «язык» (разделительное ребро) 4 - конструктивный элемент для разделения спиральной части и обводного канала.

Сечения каждого элемента строятся кривыми Безье [Математические основы машинной графики, Роджерс Д, Адаме Дж., М., Мир, 2001]. Кривые Безье - это параметрические полиномы, точки которых вычисляются по следующему алгоритму:

где X(t) и Y(t) - координаты точки на кривой,

Px_i и Py_i - координаты i-го полюса,

n - порядок кривой (порядок кривой на единицу меньше числа полюсов),

t - параметр, изменяющийся в диапазоне от 0 до 2 [Экстремальные свойства полиномов и сплайнов, Корнейчук Н.П., Бабенко В.Ф., Лигун А.А., АН Украины, Ин-т математики, Киев, Наукова думка, 1992].

Следует рассмотреть каждый из элементов и обозначить параметризуемые параметры.

Сечение спиральной части строится кривой Безье 4-го порядка (Фиг.2). Полюсами кривой являются точки P0-Р4.

Параметрами сечения являются:

- Угол α между вертикалью и прямой Р0-Р2, град,

- Ширина входа в отвод b3, мм,

- Радиус входа в отвод R3, мм,

- Пропускная способность расчетного сечения отвода A_расч, мм,

- Коэффициент отношения отрезков

который определяет радиус кривизны округления трапеции.

Сечение обводного канала строится двумя кривыми Безье 4-го порядка (Ошибка! Источник ссылки не найден. 3). Полюсами кривых являются точки Р0-Р4 и Р4-Р8. При таком построении результирующая кривая проходит чрез точку Р4, а сопряжение кривых по касательной обеспечивается расположением точек Р3 и Р5 на одной прямой Р2-Р6.

Параметрами сечения являются (Фиг.3, 4):

- толщина разделительного ребра между спиральной частью и обводным каналом, мм,

- коэффициент диффузорности канала

где F_об0 и F_обк площади первого и конечного сечения обводного канала соответственно,

- конечный угол трапеции обводного канала β. Начальный угол равен углу трапеции сечения спиральной части. От начального до конечного значения угол изменяется по линейному закону, град,

- коэффициент расширения канала

где b4₀ и b4_к ширина первого и конечного сечения обводного канала соответственно,

- коэффициент отношения отрезков

который определяет радиус кривизны округления трапеции. Параметрами диффузорной части являются (Фиг.4):

- Длина диффузора L1, мм,

- Длина разделительного ребра L2, мм,

- Диаметр выхода D, мм,

- Угол установки языка φ, град.

Переходные сечения диффузора также строятся кривыми Безье, плавно изменяющимися от последних сечений обводного канала и спиральной части до окружности диаметром D (Фиг.5).

Дуга окружности аппроксимируется кривой Безье с 4 полюсами. На Фиг.5 изображены три кривые Безье с полюсами С0-С3, С3-С6, С6-С9, аппроксимирующие окружность на выходе диффузора. Центр окружности располагается в точке С, которая расположена в середине разделительного ребра.

Чтобы получить плавность изменения формы сечений необходимо, чтобы кривые, описывающие сечения обводного канала и сечение спиральной части, плавно переходили в соответствующие кривые, аппроксимирующие окружность на выходе диффузора.

Кривая Безье, описывающая спиральную часть переходит в кривую С0-С3 посредством перемещения полюсов Р0 в С0, P1 в C1, Р2 в С2, а полюсов P3 и P4 в полюс C3′, расположенный на расстоянии половины толщины разделительного ребра под полюсом C3.

Так как сечение обводного канала описывается двумя кривыми, для получения плавности изменения формы сечений четверть дуги окружности на выходе аппроксимируется двумя кривыми с полюсами С3-С6, С6-С9. Полюса сечения перемещаются следующим образом: М0 и M1 в точку C3′′, которая расположена зеркально точке C3′ относительно горизонтали С-C3. М2 в С4, М4 в С6, М6 в С7, М7 в С8, М8 в С9. Точка М5 делит отрезок М4-М6 в том же отношении К_отн2, а точка М3 движется по отрезку М3-С5, оставаясь на пересечении с прямой М5-М4.

Сечения объединенного канала диффузора строятся таким же образом, только точки Р4, Р3, М0, M1 объединяются в одну, плавно движущуюся к точке С3 и находящуюся на пересечении горизонтали С-С3 и отрезка Р2-М2. Каждое сечение диффузора строится в соответствии с линейным увеличением площади канала по длине диффузора.

Алгоритмы построения сечений закладываются в программу, которая по заданному набору параметров выводит в файл набор точек каждого сечения, поворачивая каждое сечение вокруг оси насоса на соответствующий угол. Места сопряжений сечений реализуются посредством Безье поверхностей на четырехугольнике, построенных по имеющимся кривым.

С помощью встроенных в программу пакета инструментов облако точек преобразуется в триммированную поверхность отвода (Фиг.6) [Математические основы машинной графики, Роджерс Д, Адаме Дж., М., Мир, 2001].

В таком виде геометрия отвода загружается в программный пакет STAR CCM+ для последующего моделирования [см., например. Руководство пользователя. STAR CCM 6.02 User Guide. Режим доступа: http://www/saec.ru.24.09.2012; STAR CCM+ User Guide 6.02].

Для численного моделирования используется структурированная призматическая расчетная сетка в 5 слоев вблизи твердых стенок и неструктурированная многогранная в ядре потока.

Решение задачи построения модели потока жидкости осуществлялось при следующих граничных условиях потока:

1) Скорость на входе, причем скорость задают в виде ее проекций: радиальной и тангенциальной. Значения скоростей выбирались из теоретического расчета рабочего колеса,

2) Пограничный слой. Задаются параметры пограничного слоя на стенке проточной части,

3) Плоскость симметрии. Введение условия симметричности сокращает объем расчетной сетки вдвое, что существенно ускоряет затраты машинного времени при расчете,

4) Давление на выходе. Так как при расчете несжимаемой жидкости имеет смысл лишь перепад давления, а не его абсолютное значение, давление на выходе отвода принималось равным нулю, а потери оценивались как разность полных напоров между входом и выходом из отвода.

В качестве примера проведения процесса оптимизации был выбран отвод насоса НМ 3600-230.

Значения проекций скоростей на входе для данного типоразмера отвода следующие:

- окружная скорость V_u=44 м/с,

- радиальная скорость V_r=8,4 м/с.

Процесс оптимизации параметров состоял из двух этапов.

На первом этапе оценивалось влияние каждого геометрического параметра на течение жидкости в отводе и на его основные характеристики, выбранные в качестве критериев оптимизации, а именно потери напора в отводе и суммарная радиальная сила на роторе насоса. Результатом первого этапа явилось выявление набора параметров, оказывающих наибольшее влияние на указанные характеристики отводящего устройства, т.е. нахождение параметров оптимизации.

На втором этапе была произведена оптимизация методом ЛП-тау поиска.

При осуществлении оптимизации посредством численного моделирования можно использовать метод контрольного объема [Численные методы решения задач теплообмена и динамики жидкости, Патанкар С., М., Энергоатомиздат]. Суть метода заключается в том, что расчетная область разбивается на множество мелких ячеек, размер которых колеблется от 0,5 мм до 10 мм, каждая из которых представляет собой замкнутую область течения жидкости или газа, для которой производится поиск полей макроскопических величин (например, скорости, давления и т.п.), описывающих состояние среды во времени и удовлетворяющих определенным законам, сформулированным математически. Наиболее используемыми являются законы сохранения энергии в Эйлеровых переменных.

После первого этапа оптимизации были выявлены шесть параметров оптимизации. Параметры оптимизации и границы их изменения приведены в Таблице 1.

Метод ЛП-тау оптимизации используется при проектировании устройств, для которых сложно обосновать коэффициенты целевой функции [Численные методы Монте-Карло, И.М. Соболь, М., Наука, 1973]. В рассматриваемом случае целевую функцию можно записать следующим образом: F=a₁F1+a₂F2, где F1 - потери отвода, F2 -радиальная сила. Коэффициенты a₁ и a₂ сложно определить, т.к. сложно определить, какой из критериев является наиболее значимым.

Поэтому выбирают параметры оптимизации и задают область изменения для каждого параметра исходя из опыта проектирования подобных устройств. Если число параметров n, то область исследования - это n-мерный параллелепипед. Для поиска наилучшей комбинации параметров можно просмотреть все точки. Эти точки должны быть равномерно распределены, ЛП-тау последовательности обеспечивают равномерное расстояние между точками.

Был составлен алгоритм генерации ЛП-тау последовательности. Расчетные точки сведены в Таблицу 2.

Для каждой точки из Таблицы 2 была построена геометрия, с помощью разработанной программы автоматического построения, составлена численная модель и произведен расчет.

Чтобы минимизировать погрешности, связанные с численным расчетом, все модели рассчитывались при одинаковых параметрах расчетной сетки и с одинаковыми граничными условиями.

Результаты оптимизации отвода сведены в Таблицу 3, откуда видно, что изменение указанных геометрических параметров приводит к изменению как потерь в отводе, так и суммарной радиальной силы. Причем радиальная сила может меняться на несколько порядков. Наиболее оптимальному варианту геометрии отвода соответствует точка 13.

При этом отвод исходной конфигурации имел потери напора 10,41 м и радиальную силу 1762 Н. Оптимизированный вариант геометрии имеет как меньшие потери напора - 10,24 м, так и меньшую радиальную силу - 59,5 Н.

Такое значительное уменьшение радиальной силы, как в варианте №13, существенно улучшит эксплуатационные качества оборудования и его ресурс. Однако при этом следует иметь в виду, что радиальная сила должна в любом случае превышать минимально допустимую нагрузку на подшипниковые опоры, т.к. в противном случае будет наблюдаться повышенный износ опор ввиду их недозагрузки.

Полученные в результате оптимизации 3D-модели проточной части насосов используются как основа для изготовления с помощью 3D-принтера модели насосов из фотополимера и дальнейшей экспериментальной проверки их параметров.

Как это принято в теории подобия лопастных гидромашин, характерным размером является диаметр выхода рабочего колеса. По отношению диаметров колес модели и натуры рассчитывается масштабный коэффициент, с помощью которого определяются (из условия геометрического подобия) все остальные размеры модели. Для диагональных колес в качестве характерного диаметра выбирается диаметр выхода из колеса, взятый по средней струйке. При этом размеры модели, по возможности, должны быть максимально приближены к размерам натурного насоса для уменьшения влияния масштабного эффекта при пересчете характеристик и облегчения замеров параметров (в частности, давления) в более крупной модели насоса. Размеры модели ограничены имеющейся мощностью электродвигателя стенда и разумным диаметром трубопроводов стенда. При этом частота вращения двигателя стенда может меняться в широких пределах.

Основные формулы подобия лопастных гидромашин формулируются следующим образом:

где Н_н и Н_м - напоры натурного и модельного насоса, м,

Q_н и Q_м - подачи натурного и модельного насоса, м³/с,

N_н и N_м - мощности, потребляемые натурным и модельным насосом, Вт,

L_н и L_м - характерные линейные размеры для натурного и модельного насоса (в данном случае L_н=D_2н, L_м=D_2м), м,

n_н и n_м - частоты вращения вала натурного и модельного насоса, об/мин,

ρ_н и ρ_м - плотности жидкости, на которой проводятся испытания (в данном случае они равны), кгс/см³.

Основным параметром подобия, который вытекает из формул подобия, является коэффициент быстроходности насоса, обозначаемый n_s.

Соблюдение равенства коэффициентов быстроходности для модели и натуры (при условии соблюдения геометрического подобия элементов проточных частей) дает возможность пересчитывать характеристики насоса с модели на натуру с минимальными погрешностями (с учетом масштабного эффекта).

Для соблюдения условий подобия важно также, чтобы числа Рейнольдса для модели и натуры были либо равны (что обычно недостижимо вследствие существенной разницы размеров модели и натуры), либо кратны.

Число Рейнольдса для различных элементов проточной части насоса может рассчитываться по-разному, но в качестве интегрального параметра используется следующая формула для числа Рейнольдса:

где ω - угловая скорость вращения рабочего колеса, 1/с,

R₂ - радиус колеса на выходе из него по средней струйке,

ν - кинематический коэффициент вязкости, для воды при нормальных условиях равен 1∗10^-6 м²/с.

Радиальная сила для натурных и модельных рабочих колес может рассчитываться по эмпирической формуле:

где K_R - экспериментальный коэффициент, для данного коэффициента быстроходности равен приблизительно 0,35,

Q и Q_min (м³/с) - соответственно текущая подача насоса и подача насоса, для которой радиальная сила минимальна. Для наихудшего случая принимаем Q=0.

ρ - плотность жидкости, кг/м³,

g - ускорение свободного падения, м/с²,

H - напор насоса в данном режиме, м,

B₂ - ширина колеса на выходе с учетом толщины дисков, м,

D₂ - диаметр колеса на выходе по средней струйке, м.

При изготовлении 3D-моделей насосов их проточная часть должна выполняться в точном соответствии с геометрией 3D-моделей проточной части, разработанных для соответствующего насоса. Относительная шероховатость поверхности проточной части модели должна соответствовать относительной шероховатости поверхности натурного насоса. Конструкция моделей должна обеспечивать простоту сборки и разборки модельного насоса в процессе проведения испытаний, а также позволять в процессе испытаний проводить замеры давлений в заданных точках проточной части (всего около 30 точек) для верификации данных, полученных путем численного моделирования. В конструкции должна быть предусмотрена возможность замера сил на опорах насоса в плоскостях, перпендикулярных оси вращения, для уточнения расчета подшипниковых опор натурного насоса и верификации расчетных данных по величине и направлению действия радиальных сил. Для выполнения указанных требований модель насоса можно, например, изготавливать из фотополимера с помощью 3D-принтера в виде двух тонкостенных сборных оболочек. Снаружи, для увеличения жесткости, оболочки обклеиваются стеклопластиком. Для восприятия гидравлических сил, возникающих в проточной части насоса, обе тонкостенные оболочки крепятся шпильками, на них наносится слой эпоксидной смолы, а затем оболочки заливаются с помощью внешней опалубки цементной смесью, после чего дополнительно стягиваются установленными снаружи дополнительными длинными шпильками. Для замера давлений и иных параметров в оболочках выполнены отверстия, где установлены штуцеры. После изготовления модели насоса ее устанавливают на испытательном стенде, подключают измерительную аппаратуру и проводят гидравлические испытания. При этом в процессе испытаний необходимо решить следующие основные задачи:

а) получить нормальные характеристики модельных насосов, пересчитать их на основе теории подобия с учетом масштабного эффекта на натурные размеры насосов и подтвердить (или опровергнуть) правильность теоретических расчетов и численной оптимизации проточных частей;

б) провести балансовые испытания моделей насосов с целью выделить основные составляющие КПД насоса и разработать меры по их повышению.

Проведение испытаний моделей насоса и получение их характеристик является необходимым условием верификации данных, полученных расчетным путем (как методами классической теории лопастных гидромашин, так и методами гидродинамического моделирования). По результатам испытаний можно принимать решения о соответствии (или несоответствии) расчетных данных экспериментальным и возможности изготовления опытного образца насоса в натуральную величину для испытаний на стенде или о необходимости продолжения гидравлических испытаний модели насоса при внесении необходимых коррекций в используемую математическую модель течения жидкости в насосе и построение отвода и подвода.

После проведения испытаний выполняется пересчет полученных характеристик с модели насоса (макета) на натурный насос.

Испытания проводят при различных частотах вращения вала, например: 700, 1000, 1500, 2000 об/мин. При этом одна из частот выбирается в качестве базовой, например частота 2000 об/мин, а испытания при других частотах вращения проводились для уточнения влияния частоты вращения на КПД насоса и накопления общей статистики параметров и характеристик макета.

Общеизвестно [Лабораторный курс гидравлики, насосов и гидропередач. Под ред. Руднева С.С. и Подвидза Л.Г., М., Машиностроение, 1974], что КПД уменьшенного макета всегда значительно меньше, чем у натурного насоса (что является следствием масштабного эффекта), поэтому необходимо пересчитать полученные в ходе испытаний параметры модели на натуру. При этом должны учитываться следующие факторы:

1) увеличение общего КПД насоса при увеличении частоты вращения вала;

2) увеличение гидравлического КПД насоса при увеличении размеров проточной части;

3) увеличение механического КПД вследствие снижения доли механических потерь в общем балансе энергии насоса;

4) повышение объемного КПД вследствие уменьшения относительной величины зазора в щелевых уплотнениях натурного насоса по сравнению с моделью;

Известны методы пересчета характеристик насоса с учетом масштабного эффекта [Лопастные насосы. Справочник, Под ред. Зимницкого В.А. и Умова В.А., Л., Машиностроение, 1986], [Лопастные насосы, Михайлов А.К., Малюшенко В.В., М., Машиностроение, 1977, стр.9], основанные на применении эмпирических формул, учитывающих изменение частоты вращения, размеров и вязкости рабочей жидкости при переходе от модели к натуре.

Однако для более точного определения влияния масштабного эффекта в дополнении к расчетам по эмпирическим формулам необходимо экспериментально выделить в общем балансе потерь в насосном агрегате величины потерь отдельных видов (гидравлических, объемных, механических), чтобы затем пересчитать каждый из слагающих общего КПД насоса по отдельной формуле и получить прогнозное значение общего КПД.

В процессе проведения балансовых испытаний на стенде проводят замеры момента на валу модели и частоты вращения вала. По этим величинам определятся величина механических потерь в насосе. Замеряется расход жидкости через щелевые уплотнения вращающегося колеса. Величина этого расхода дает возможность определить действительное значение объемного КПД. Для разделения механических потерь в насосе на внешние и внутренние можно также дополнительно снять с вала колесо, собрать насос с валом без колеса и испытать его при базовой частоте вращения. При этом определяется значение момента на валу, соответствующее величине внешних механических потерь в насосе (потери в подшипниках, уплотнениях, муфте). Дополнительно можно замерить величины перетечек при невращающемся вале и нескольких значениях давления на нагнетании, для уточнения влияния скорости движения внутреннего кольца щелевого уплотнения на перетечку в нем.

По результатам балансовых испытаний определяют значения объемного, гидравлического и механического КПД, значения которых используются для учета масштабного эффекта и пересчета характеристик модели на натурный насос, за исключением механического КПД, который для модели сильно занижен по сравнению с натурным насосом вследствие особенностей конструкции модели.

Пересчет величин объемного, гидравлического и механического КПД проводится по эмпирическим формулам, учитывающим влияние масштабного эффекта, а затем рассчитанные коэффициенты пересчета применяются к величинам КПД, полученным при балансовых испытаниях, и на их основе рассчитываются прогнозные характеристики натурного насоса.

При пересчете с модели на натуру заранее известен масштабный коэффициент, равный отношению внешнего диаметра рабочего колеса модельного насоса к тому же диаметру натурного насоса.

Влияние изменения размеров и параметров насоса на величину гидравлического КПД может быть рассчитано, например, по следующей формуле [Лопастные насосы. Справочник, Под ред. Зимницкого В.А. и Умова В.А., Л., Машиностроение]:

где η_Гн - гидравлический КПД натурного (большого) насоса,

η_Гм - гидравлический КПД модельного (малого) насоса,

Dq - коэффициент подачи, определяемый по следующей формуле:

где Q - подача насоса, м³/с,

n - частота вращения вала насоса, об/мин.

Используется и другая формула для пересчета гидравлического КПД с учетом диаметра входа в рабочее колесо насоса [Лопастные насосы, Михайлов А.К., Малюшенко В.В., М., Машиностроение, 1977, стр.9]:

где D_1прM - приведенный диаметр входа рабочего колеса модельного насоса, м,

D_1прН - приведенный диаметр входа рабочего колеса натурного насоса, м.

Пересчет величины механического КПД с модели на натуру осложнен разными типами подшипников в модельном и натурном насосах. Однако предварительно можно использовать следующую формулу [Лопастные насосы, Михайлов А.К., Малюшенко В.В., М., Машиностроение, 1977, стр.9]:

где η_Мм - механический КПД модельного насоса,

η_Мн - механический КПД натурного насоса,

R_2M - радиус выхода рабочего колеса модельного насоса,

R_2H - радиус выхода рабочего колеса натурного насоса,

n_М - частота вращения вала модельного насоса,

n_Н - частота вращения вала натурного насоса,

ν_M - вязкость рабочей жидкости модельного насоса,

ν_H - вязкость рабочей жидкости натурного насоса.

Рассчитанное по вышеприведенной формуле отношение механического КПД модели и натуры η_Мм/η_Мн можно обозначить К_ηМ.

Вязкость рабочей жидкости у модели и у натуры равна, т.к. они испытываются на воде. Точное определение объемного КПД затруднено из-за первоначального отсутствия экспериментальных данных по натурному насосу, однако, основываясь на имеющемся опыте создания центробежных насосов, можно принять значение коэффициента отношений объемного КПД модельного (η_Oм) и натурного (η_Ом) насоса K_ηО равным 0,98 в зависимости от мощности насоса и объема перекачиваемой им жидкости.

Суммируя полученные выше данные, можно определить величину коэффициента приращения общего КПД при переходе от модели к натуре. Этот коэффициент будет определяться как произведение всех трех полученных выше коэффициентов и рассчитывается по формуле:

K_η=K_ηГK_ηMK_ηO

С учетом приведенных коэффициентов пересчета можно построить прогнозную характеристику натурного насоса, исходя из характеристики модельного насоса. При этом значения напора насоса получают, корректируя величину напора модельного насоса на величину коэффициента K_ηГ, а значения КПД натурного насоса - на величину коэффициента K_η.

Характеристики строятся на основании расчетов по эмпирическим формулам, учитывающим масштабный эффект. Использование данных, полученных по результатам балансовых испытаний макета, позволяет уточнить эти характеристики.

Полученные