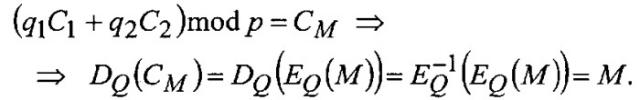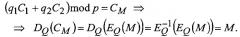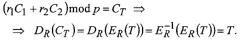Способ шифрования блока двоичных данных

Способ шифрования блока двоичных данных

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов и устройств для защиты информации, передаваемой по телекоммуникационным сетям путем шифрования сообщений (информации).

Известны способы шифрования электронных сообщений, представленных в цифровом виде, а именно в виде двоичных данных, выполняемые по секретному ключу, например способ, реализованный в виде алгоритма блочного шифрования RC5 [B.Schneier, "Applied Cryptography", Second Eddition, John Wiley & Sons, Inc., New York, 1996, рр. 344-346]. Способ включает в себя формирование секретного ключа в виде совокупности подключей, разбиение n-битового двоичного блока информации на n/2-битовые информационные подблоки А и В и поочередное преобразование этих подблоков. Подблоки преобразуются путем последовательного выполнения над ними линейных и нелинейных операций, в качестве которых используются операции суммирования по модулю 2^m, где m=n/2=8,16,32,64, поразрядного суммирования по модулю 2 и циклического сдвига влево, причем число бит, на которое сдвигается преобразуемый подблок, зависит от значения другого подблока. Последнее свойство является характерным для способа RC5 и определяет зависимость операции циклического сдвига на текущем шаге преобразования подблока от исходного значения входного блока данных. Подблок информации, например подблок В, преобразуют путем наложения подблока А на подблок В с помощью операции поразрядного суммирования по модулю 2 В:=В⊕А. После этого над подблоком В выполняют операцию циклического сдвига влево на число бит, равное значению подблока А:В:=В<<<А. Затем над подблоком В и одним из подключей К выполняют операцию суммирования по модулю 2^m, где m - длина подблока в битах: B:=(B+K)mod 2^m. После этого аналогичным образом преобразуется подблок А. В зависимости от размеров ключа выполняется несколько таких итераций преобразования обоих подблоков. Данный способ обеспечивает достаточно высокую скорость шифрования при программной реализации. Недостатком способа шифрования RC5 является невысокая стойкость к дифференциальному и линейному видам криптоанализа [Kaliski B.S., Yin Y.L. On Differential and Linear Cryptanalysis of the RC5 Encryption Algorithm. Advances in Cryptology - CRYPTO 95. Proceedings, Springer-Verlag, 1995, pp. 171-184].

Известен способ шифрования n-битовых блоков данных [B.Schneier, "Applied Cryptography", Second Eddition, John Wiley & Sons, Inc., New York, 1996, pp. 193-194] путем генерации секретного ключа К, разбиения сообщения М на n-битовые блоки данных М₁, М₂,…,М_k, где k - число блоков в сообщении; n≥64 бит, и последующего шифрования блоков данных М₁, М₂,…М_k, причем процесс шифрования выполняют следующим путем. Шифруют блок М₁ по секретному ключу, получая блок криптограммы C₁, затем, начиная со значения i-2 и до значения i=k, суммируют с помощью операции поразрядного суммирования блок криптограммы C_i-1 и блок M_i, полученный в результате суммирования блок данных шифруют по секретному ключу, получая в результате текущий блок криптограммы С_i. Совокупность блоков криптограммы C₁, C₂,…, C_k представляет собой криптограмму, содержащую сообщение М в скрытом виде. Извлечение сообщения М из криптограммы практически возможно только с использованием секретного ключа, использованного при шифровании, за счет чего достигается защита информации, содержащейся в сообщении М, при его передаче по открытым каналам связи. Данный способ обеспечивает улучшение статистических свойств криптограммы, однако он имеет недостаток, состоящий в том, что теряется возможность независимого расшифрования отдельных блоков криптограммы.

Наиболее близким по своей технической сущности к заявляемому способу шифрования n-битового блока двоичных данных М является способ, описанный в патенте №2459275 [Молдовян А.А., Молдовян Н.А. Способ блочного шифрования сообщения М, представленного в двоичном виде. Патент №2459275] по п.2 формулы изобретения указанного патента. Способ прототип включает в себя формирование секретного ключа, включающего подключи Q и R, формирование вспомогательного n-битового блока двоичных данных Т, формирование n-битовой вспомогательной криптограммы С_M путем выполнения над М операции блочного шифрования E в зависимости от Q по формуле С_M=E_Q(M), формирование n-битовой вспомогательной криптограммы C_T путем выполнения над Т операции блочного шифрования E в зависимости от R по формуле C_T=E_R(T), формирование криптограммы С в зависимости от секретного ключа и вспомогательных криптограмм C_M и C_T.

Способ-прототип позволяет реализовать защиту информации с использованием механизма обманных ловушек, который состоит в том, что потенциальному злоумышленнику подставляется часть секретного ключа, включающая подключ R, в качестве ключа расшифрования, а в качестве вспомогательного n-битового блока двоичных данных Т используется n-битовый блок фиктивного сообщения. Блок криптограммы С расшифровывается путем его преобразования по дополнительному ключу, приводящего к получению вспомогательной криптограммы С∗, представляющей собой конкатенациию двух n-битовых строк C_M и C_T:С∗=C_M||C_T. Затем правая n-битовая строка C_T расшифровывается путем выполнения операции блочного преобразования D, обратной к операции блочного шифрования Е, т.е. по формуле Т=D_R(C_T). Аналогичная процедура расшифрования выполняется с использованием подключа К и левой n-битовой строки C_M вспомогательной криптограммы C∗=C_M||C_T. Недостатком способа прототипа является то, что различные части вспомогательной криптограммы C∗ используются при расшифровании блока данных М и блока фиктивного сообщения Т. Это демаскирует факт наличия в блоке криптограммы С блока данных М.

Задачей заявленного нового технического решения является разработка способа шифрования блока двоичных данных, представленного в виде n-битовой строки, обеспечивающего эффективную маскировку факта наличия n-битового блока данных М в блоке криптограммы С за счет того, что при выполнении процедуры расшифрования осуществляется преобразование С в n-битовую вспомогательную криптограмму и использование всех битов вспомогательной криптограммы при выполнении процедур расшифрования как n-битового блока данных М, так и вспомогательной n-битовой строки Т.

Техническим результатом нового способа шифрования блока двоичных данных М является повышение уровня защищенности информации, шифруемой с его применением.

Указанный технический результат достигается тем, что в способе шифрования блока двоичных данных М, заключающемся в формировании секретного ключа, включающего подключи Q и R, формировании вспомогательного n-битового блока двоичных данных T, формировании n-битовой вспомогательной криптограммы C_M путем выполнения над М операции блочного шифрования Е в зависимости от Q по формуле C_M=E_Q(M), формировании n-битовой вспомогательной криптограммы C_T путем выполнения над Т операции блочного шифрования Е в зависимости от R по формуле C_T=E_R(T), формировании криптограммы С в зависимости от секретного ключа и вспомогательных криптограмм C_M и C_T,

новым является то, что подключ Q формируют в виде 2n-битовой строки, представляющей собой конкатенацию двух n-разрядных двоичных чисел q₁ и q₂, подключ R формируют в виде 2n-битовой строки, представляющей собой конкатенацию двух n-разрядных двоичных чисел r₁ и r₂, формируют (n+1)-разрядное двоичное число p и формируют криптограмму С в виде конкатенации двух многоразрядных двоичных чисел C₁ и C₂, являющихся решением системы из двух линейных уравнений k₁C₁+k₂C₂=C_M mod p и q₁C₁+q₂C₂=C_T mod р с двумя неизвестными C₁ и C₂.

Новым также является то, что формируют (n+1)-разрядное двоичное число p, которое является простым.

Формирование и использование простого (n+1)-разрядного двоичного числа p упрощает процедуру генерации подключей Q и R.

Новым является и то, что формируют (n+1)-разрядное двоичное число p, которое представимо в виде 2ⁿ+1.

Использование в качестве (n+1)-разрядного двоичного числа р МДЧ вида 2ⁿ+1 обеспечивает формирование криптограммы, имеющей размер 2n бит, что упрощает программную и аппаратную реализацию заявленного способа шифрования n-битового блока двоичных данных М.

Благодаря указанной новой совокупности существенных признаков за счет формирования n-битовых вспомогательных криптограмм C_M и C_T обеспечивается использование всех битов вспомогательной криптограммы при выполнении процедуры расшифрования как блока данных М, так и вспомогательного n-битового блока двоичных данных Т, в качестве которой может быть применен n-битовой блок некоторого фиктивного сообщения. Это обеспечивает эффективную маскировку факта наличия n-битового блока данных М в блоке криптограммы С при ее расшифровании потенциальным нарушителем при использовании им подключа Q при расшифровании криптограммы С, поскольку процедура расшифрования выполняется по одной и той же формуле как при расшифровании блока данных M, так и при расшифровании блока фиктивного сообщения Т.

Корректность заявленного способа шифрования n-битового блока двоичных данных М состоит в том, что по криптограмме С=С₁||C₂, где знак || обозначает операцию конкатенации (объединения битовых строк), может быть восстановлен «-битовый блок двоичных данных М по подключу Q=q₁||q₂ по формуле M=D_Q((q₁C₁+q₂C₂)mod p), где D - операция блочного расшифрования, обратная операции блочного шифрования Е, и вспомогательный n-битовый блок двоичных данных Т по подключу R=r₁||r₂ по формуле T=D_R((r₁C₁+r₂C₂)mod р).

Действительно, при выполнении процедуры расшифрования по подключу Q=q₁||q₂ имеем

а при выполнении процедуры расшифрования по подключа R=r₁||r₂ имеем

Далее реализуемость и корректность заявленного способа шифрования n-битового блока двоичных данных М иллюстрируется частными примерами его реализации.

Пример 1. Шифрование 64-битового блока двоичных данных М. Формируют простое МДЧ р=18446744073709551629₁₀=2⁶⁴+2³+2²+1=

=10000000000000000000000000000000000000000000000000000000000001101₂, , где индекс 10 (индекс 2) обозначает то, что число записано с использованием десятичной (двоичной) системы записи чисел, формируют секретный ключ в виде подключей Q и R, причем подключ Q формируют в виде 128-битовой строки, представляющей собой конкатенацию двух 64-разрядных двоичных чисел q₁ и q₂, т.е. Q=q₁||q₂, а подключ R формируют в виде 128-битовой строки, представляющей собой конкатенацию двух 64-битовых строк r₁ и r₂ (т.е. R=r₁||r₂), которые удовлетворяют условиям

q₁≡q₂≡r₁≡r₂≡1 mod 2 (условие нечетности чисел q₁, q₂, r₁, r₂), а именно формируют следующие МДЧ:

q₁=15344089324516380789₁₀; q₂=12571778644096321013₁₀;

r₁=15608185472029694193₁₀; r₂=15369129295277581477₁₀.

Проверка показывает, что сформированные нечетные МДЧ q₁, q₂, r₁ и r₂ удовлетворяют условию q₁r₂-q₂r₁=812714980881351227≠0 mod p. Затем формируют вспомогательный 64-битовый блок двоичных данных Т и 64-битовую вспомогательную криптограмму С_M путем выполнения над блоком данных М операции блочного шифрования Е в зависимости от подключа Q=q₁||q₂ по формуле C_M=E_Q(M), где операция блочного шифрования описывается следующим алгоритмом:

1. Установить значение счетчика i←0 и переменной C_M←М, где знак ← обозначает операцию присваивания.

2. Сформировать 64-битовую строку C_M в виде МДЧ, вычисленного по формуле C_M←(q₁C_M mod2⁶⁴)^<29<, где (…)^<29< обозначает операцию циклического сдвига битовой строки (…) на 29 бит влево.

3. Преобразовать 64-битовую строку C_M по формуле C_M←(q₁C_M mod2⁶⁴)^<17<, где (…)^<17< обозначает операцию циклического сдвига битовой строки (…) на 17 бит влево.

4. Прирастить значение счетчика i:i←i+1. Если i<16, то перейти к шагу 2, в противном случае текущее значение C_M взять в качестве выходного значения операции блочного шифрования E_Q, выполненной над 64-битовым блоком двоичных данных М.

Затем формируют 64-битовую вспомогательную криптограмму C_T путем выполнения над вспомогательным 64-битовым блоком двоичных данных Т операции блочного шифрования Е в зависимости от подключа R=r₁||r₂ по формуле C_T=E_R(T) в соответствии со следующим алгоритмом:

1. Установить значение счетчика i←0 и переменной C_T←Т.

2. Сформировать 64-битовую строку C_T в виде МДЧ, вычисленного по формуле C_T←(r₁C_T mod2⁶⁴)^<29<.

3. Преобразовать 64-битовую строку C_T по формуле C_T←(r₂C_T mod2⁶⁴)^<17<.

4. Прирастить значение счетчика i:i←i+1. Если i<16, то перейти к шагу 2, в противном случае текущее значение C_T взять в качестве выходного значения операции блочного шифрования E_R, выполненной над вспомогательным 64-битовым блоком двоичных данных Т.

После формирования вспомогательных криптограмм C_M и C_T, рассматривая их как 64-битовые МДЧ, формируют криптограмму C=C1||C₂ путем решения следующей системы из двух линейных уравнений с неизвестными C₁ и C₂.

Решением данной системы являются два МДЧ C₁ и C₂, которые объединяются в криптограмму C=C₁||C₂.

Доказательство корректности данного частного варианта реализации заявленного способа шифрования n-битового блока двоичных данных М доказывается аналогично описанному ранее общему доказательству корректности заявленного способа с учетом того, что для нечетных МДЧ q_1, q₂, r₁, r₂ по модулю 2⁶⁴ существуют и легко вычисляются по расширенному алгоритму Евклида соответствующие обратные значения q 1 − 1 , q 2 − 1 , r 1 − 1 , r 2 − 1 а операция блочного расшифрования D_Q(C_M), обратная операции блочного шифрования E_Q(M), реализуется следующей процедурой преобразования:

1. Установить значение счетчика i←0 и переменной M←C_M.

2. Преобразовать 64-битовую строку М, выполняя последовательно вычисления по формулам М←М^>17> и M ← M q 2 − 1   mod 2 64 , где (…)^>17> обозначает операцию циклического сдвига битовой строки (…) на 17 бит вправо.

3. Преобразовать 64-битовую строку М, выполняя последовательно вычисления по формулам М←М^>29> и M ← M q 1 − 1   mod 2 64 , , где (…)^>29> обозначает операцию циклического сдвига битовой строки (…) на 29 бит вправо.

4. Прирастить значение счетчика i:i←i+1. Если i<16, то перейти к шагу 2, в противном случае текущее значение М взять в качестве выходного значения операции D_Q, выполненной над 64-битовой вспомогательной криптограммой C_M.

Аналогично записывается процедура для реализации операции блочного расшифрования D_R(C_T), обратная операции блочного шифрования E_R(T).

Рассмотренная частная реализация заявленного способа может быть применена для совместного шифрования двух сообщений Message и Text, каждое из которых, например, имеет размер 64 Кбит. Сообщение Message разбивается на 64-битовые блоки данных M₁, M₂,…,M_w, где w=1000. Сообщение Text разбивается на 64-битовые блоки данных T₁, T₂,…,T_w. Поочередно для значений i=1, 2,…, 1000 пары блоков данных (M_i, T_i) совместно шифруются в соответствии с описанным примером реализации заявленного способа, в результате чего формируется шифртекст в виде последовательности 128-битовых криптограмм (C₁||C₂)_i, i=1, 2,…,1000.

Пример 2. Шифрование 128-битового блока двоичных данных М.

Формируют МДЧ p вида 2¹²⁸+1:

р=2¹²⁸+1=340282366920938463463374607431768211457₁₀, где индекс 10 обозначает то, что число записано с использованием десятичной системы записи чисел. В виде двоичного числа (т.е. при использовании двоичной системы записи чисел) р имеет вид

р=1000000000000000000000000000000000000000000000000000000000000 00\\0000000000000000000000000000000000000000000000000000000000000 00001₂,

где знак «\\» означает перенос записи на следующую строку. Затем формируют секретный ключ в виде подключей Q и R, причем подключ Q формируют в виде 256-битовой строки, представляющей собой конкатенацию двух 128-разрядных двоичных чисел q₁ и q₂, т.е. Q=q₁||q₂, а подключ R формируют в виде 256-битовой строки, представляющей собой конкатенацию двух 128-битовых строк r₁ и r₂ (т.е. R=r₁||r₂), которые удовлетворяют условию

q₁≡q₂≡r₁≡r₂≡1 mod 2 (условие нечетности чисел q₁, q₂, r₁, r₂), а именно формируют следующие МДЧ:

q₁=321909040675575663770595377008565615669₁₀;

q₂=286307205067618230636306150613625759003₁₀;

r₁=290440427634195645156881834450918186151₁₀;

r₂=294266926927583280559101629113993987661₁₀.

Проверка показывает, что сформированные нечетные МДЧ q₁, q₂, r₁, и r₂ удовлетворяют условию

q₁r₂-q₂r₁=75227762587413192201808942155507758598≠0 mod р.

Затем формируют вспомогательный 64-битовый блок двоичных данных Т и 128-битовую вспомогательную криптограмму C_M путем выполнения над блоком данных М операции блочного шифрования Е в зависимости от подключа Q=q₁||q₂ по формуле C_M=E_Q(M), где операция блочного шифрования описывается следующим алгоритмом:

1. Установить значение счетчика i←0 и переменной C_M←М.

2. Сформировать 64-битовую строку C_M в виде МДЧ, вычисленного по формуле C_M←(q₁C_M mod2¹²⁸)^<32<, где (…)^<32< обозначает операцию циклического сдвига битовой строки (…) на 32 бита влево.

3. Преобразовать 64-битовую строку C_M по формуле C_M←(q₂C_M mod2¹²⁸)^<40<, где (…)^<40< обозначает операцию циклического сдвига битовой строки (…) на 40 бит влево.

4. Прирастить значение счетчика i:i←i+1. Если i<16, то перейти к шагу 2, в противном случае текущее значение C_M взять в качестве выходного значения операции блочного шифрования E_Q, выполненной над 64-битовым блоком двоичных данных М.

Затем формируют 64-битовую вспомогательную криптограмму C_T путем выполнения над вспомогательным 64-битовым блоком двоичных данных Т операции блочного шифрования Е в зависимости от подключа R=r₁||r₂ по формуле C_T=E_R(T) в соответствии со следующим алгоритмом:

1. Установить значение счетчика i←0 и переменной C_T←Т.

2. Сформировать 64-битовую строку C_T в виде МДЧ, вычисленного по формуле C_T←(r₁C_T mod2¹²⁸)^<32<.

3. Преобразовать 64-битовую строку C_T по формуле C_T←(r₂C_T mod2¹²⁸)^<40<.

4. Прирастить значение счетчика i:i←i+1. Если i<16, то перейти к шагу 2, в противном случае текущее значение C_T взять в качестве выходного значения операции блочного шифрования E_R, выполненной над вспомогательным 64-битовым блоком двоичных данных Т.

После формирования вспомогательных криптограмм C_M и C_T, рассматривая их как 64-битовые МДЧ, формируют криптограмму C=C₁||C₂ путем решения следующей системы из двух линейных уравнений с неизвестными C₁ и C₂:

Решением данной системы являются два МДЧ C₁ и C₂, которые объединяются в криптограмму C=C₁||C₂.

Доказательство корректности данного частного варианта реализации заявленного способа шифрования n-битового блока двоичных данных М доказывается аналогично описанному ранее общему доказательству корректности заявленного способа с учетом того, что для нечетных МДЧ q₁, q₂, r₁, r₂ по модулю 2¹²⁸ существуют и легко вычисляются по расширенному алгоритму Евклида соответствующие обратные значения q 1 − 1 ,   q 2 − 1 ,   r 1 − 1 ,   r 2 − 1 , операция блочного расшифрования D_Q(C_M), обратная операции блочного шифрования E_Q(M), реализуется следующей процедурой преобразования:

1. Установить значение счетчика i←0 и переменной M←C_M.

2. Преобразовать 64-битовую строку М, выполняя последовательно вычисления по формулам М←М^>40> и M ← M q 2 − 1   mod 2 128 , где (…)^>40> обозначает операцию циклического сдвига битовой строки (…) на 40 бит вправо.

3. Преобразовать 64-битовую строку М, выполняя последовательно вычисления по формулам М←М^>32> и M ← M q 2 − 1   mod 2 128 , где (…)^>32> обозначает операцию циклического сдвига битовой строки (…) на 32 бита вправо.

4. Прирастить значение счетчика i:i←i+1. Если i<16, то перейти к шагу 2, в противном случае текущее значение М взять в качестве выходного значения операции D_Q, выполненной над 64-битовой вспомогательной криптограммой C_M.

Аналогично записывается процедура для реализации операции блочного расшифрования D_R(C_T), обратная операции блочного шифрования E_R(T).

Рассмотренная частная реализация заявленного способа может быть применена для совместного шифрование двух сообщений Message и Text, каждое из которых, например, имеет размер 128 Кбайт. Сообщение Message разбивается на 128-битовые блоки данных M₁, M₂,…, M_w, где w=8000. Сообщение Text разбивается на 128-битовые блоки данных T₁, T₂,…, T_w. Поочередно для значений i=1, 2,…, 8000 пары блоков данных (M_i, T_i) совместно шифруются в соответствии с описанным примером реализации заявленного способа, в результате чего формируется шифртекст в виде последовательности 256-битовых криптограмм (C₁||C₂)_i, i=1, 2,…, 8000.

Приведенные примеры показывают, что заявляемый способ шифрования блока данных М, представленного в виде n-битовой строки, функционирует корректно, технически реализуем и позволяет решить поставленную задачу.

Заявляемый способ шифрования блока данных М, представленного в виде n-битовой строки, может быть применен для разработки средств комплексной защиты информации от несанкционированного доступа, обеспечивающих дополнительную защищенность информации за счет навязывания потенциальным злоумышленникам ложных сообщений. Данный способ также может быть применен для защищенной широковещательной рассылки сообщений с управлением доступа к сообщениям со стороны получателей при обеспечении идентичности процедуры расшифрования одной и той же криптограммы. Такие средства защищенной широковещательной рассылки сообщений решают задачу неотслеживаемости трафика при передаче информации по телекоммуникационным каналам.

1. Способ шифрования блока двоичных данных (М), заключающийся в формировании секретного ключа, включающего подключи Q и R, формировании вспомогательного n-битового блока двоичных данных Т, формировании n-битовой вспомогательной криптограммы C_M путем выполнения над М операции блочного шифрования E в зависимости от Q по формуле C_M=E_Q(M), формировании n-битовой вспомогательной криптограммы C_T путем выполнения над Т операции блочного шифрования E в зависимости от R по формуле C_T=E_R(T), формировании криптограммы С в зависимости от секретного ключа и вспомогательных криптограмм C_M и C_T, отличающийся тем, что подключ Q формируют в виде 2n-битовой строки, представляющей собой конкатенацию двух n-разрядных двоичных чисел q₁ и q₂, подключ R формируют в виде 2n-битовой строки, представляющей собой конкатенацию двух n-разрядных двоичных чисел r₁ и r₂, формируют (n+1)-разрядное двоичное число p и формируют криптограмму С в виде конкатенации двух многоразрядных двоичных чисел C₁ и C₂, являющихся решением системы из двух линейных уравнений q₁C₁+q₂C₂=C_M mod р и r₁C₁+r₂C₂=C_T mod р с двумя неизвестными C₁ и C₂.

2. Способ по п.1, отличающийся тем, что формируют (n+1)-разрядное двоичное число p, которое является простым.

3. Способ по п.1, отличающийся тем, что формируют (n+1)-разрядное двоичное число p, которое представимо в виде 2ⁿ+1.